УДК 621.391, 621.396

ПРИЕМ ХАОТИЧЕСКИХ СИГНАЛОВ С ИСПОЛЬЗОВАНИЕМ ОПОРНОГО ГЕНЕРАТОРА ХАОСА

Ю. А. Дмитриев¹, Л. В. Кузьмин ²

¹ Московский физико-технический институт

² Институт радиотехники и электроники им. В.А. Котельникова РАН

 

Получена 26 января 2012 г.

Аннотация. В работе предлагается новая схема некогерентного приема для систем связи, использующих в качестве носителя информации хаотические радиоимпульсы. Проведено предварительное исследование предложенной схемы и показана ее работоспособность и эффективность в качестве приемника для хаотических радиоимпульсов.

Ключевые слова: хаос, хаотические радиоимпульсы, системы передачи информации, некогерентный прием.

Abstract. This paper proposes a new scheme for noncoherent reception for communication systems, using as information carrier chaotic radio pulses. The preliminary study was done of the proposed scheme and its effectiveness as a receiver for chaotic radio pulses was shown.

Keywords: chaos, chaotic radio pulses, communication system, incoherent reception.

 

Введение

Исследования по использованию хаотических сигналов для передачи информации ведутся более 25 лет [1]. На первом этапе для этой цели было предложено несколько схем применения хаотических сигналов, использующих явления хаотического синхронного отклика и хаотической синхронизации. Так, для скрытной передачи полезного сигнала были предложены схемы хаотической маскировки [2], схема с нелинейным подмешиванием информационного сигнала в хаотический [1,3,4] и инверсная схема [5], а для передачи цифровой информации был предложен метод переключения хаотических режимов (chaotic shift keying - CSK) [6-8]. В дальнейшем от идеи использования хаотической синхронизации для организации передачи информации отказались из-за низкой устойчивости схем основанных на ней к шумам и искажениям в канале связи. Вместо схем использующих хаотическую синхронизацию были предложены схемы использующие относительный прием (differential chaotic shift keying - DСSK) [9] и энергетический прием [10,11].

Так, прямохаотическая схема передачи информации с энергетическим приемом к настоящему времени практически реализована в ряде систем передачи информации [12] и вошла как опциональное решение в стандарты сверхширокополосной беспроводной персональной связи IEEE 802.15.4a. [13].

В этой схеме передача информации осуществляется с помощью хаотических радиоимпульсов расположенных на определенной позиции временной оси. Для передачи единицы используется импульс для передачи нуля пробел. Так, например, для передачи сигнала 1, 0, 1 используется наличие импульса на первой позиции, отсутствие на второй позиции и наличие импульса на третьей позиции (рис. 1).

 

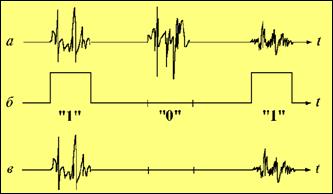
Рис.1. Передача информации с помощью хаотических радиоимпульсов (а – исходный сигнал; б – модуляция информационным сигналом; в – итоговый (восстановленный) поток импульса после модуляции).

Скорость передачи информации с помощью таких систем варьируется от единиц Кбит/сек до сотен Мбит/сек. В качестве приемника в таких системах используются приемники на основе детектора огибающей. При этом в силу малого уровня мощности входной сигнала его перед детектированием необходимо усиливать.

В настоящей работе вводится альтернативная схема энергетического приема хаотических радиоимпульсов, не требующая предварительного усиления сигнала.

Схема некогерентного приема

На рис. 2 представлена стандартная структура приемника огибающей хаотических радиоимпульсов, состоящая из усилителя, квадратичного детектора, фильтра нижних частот и порогового устройства.

 

Рис. 2. Структура используемого приемника.

 

Предлагаемая альтернативная схема некогерентного приема хаотических радиоимпульсов показана на рис. 3.

 

 

Рис. 3. Предлагаемая альтернативная схема приемника.

Она включает в себя: опорный генератор хаоса (ГХ), задержку (), два перемножителя (Х), два фильтра нижних частот (ФНЧ), два квадратичных детектора , сумматор ( и пороговое устройство (  ).

В этой схеме входной сигнал разделяется на 2 части, каждый из которых поступает соответственно на первый и второй перемножители. В первом перемножителе происходит перемножение поступившего сигнала с сигналом опорного генератора хаоса. А во втором перемножителе поступающий со входа сигнал перемножается с сигналом от опорного генератора хаоса, задержанного на величину, равную четверти периода его автокорреляционной функции. Такой сигнал в среднем ортогонален сигналу без задержки.

Получаемые после перемножения в каждой из ветвей сигналы, пропускается через фильтр нижних частот, согласованных по частоте среза с длинами хаотических радиоимпульсов, возводятся в квадрат и суммируются, после чего суммарный сигнал поступают на вход порогового устройства. На основе отклика порогового устройства принимается решение о наличии импульса или его отсутствии.

Отметим, что предположительно такая схема будет эффективно работать в случае, когда автокорреляционная функция процессов в опорном генераторе хаоса спадает достаточно медленно, а генератор хаоса в передатчике и опорный генератор хаоса в приемнике не значительно различаются по своим характеристикам. Для того чтобы определить степень и эффективность работоспособности предлагаемого приемника необходимо произвести математическое моделирование работы схемы с учетом несовпадения параметров в передающей и приемной системах и несовпадениях начальных условий.

Моделирование

При моделировании предлагаемой схемы приема в качестве модели генератора хаоса используется система Ресслера [14], описываемая уравнениями (1).

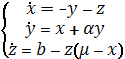,                                                (1)

где , b и  - параметры.

Моделирование производится при значениях параметров  , значение параметра  в опорном генераторе хаоса в приемнике было равно , а значение параметра при формировании хаотических радиоимпульсов в передатчике варьировалось с целью моделирования различий в характеристиках генератора приемника и передатчика.

На рис. 4 показан фазовый портрет системы Ресслера при значениях параметров, соответствующих модели опорного генератора хаоса в приемнике.

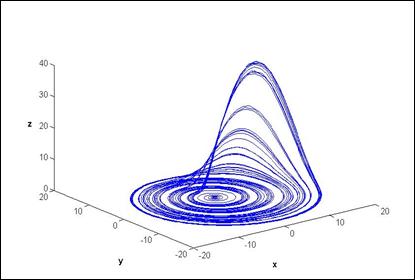
Рис. 4. Фазовый портрет системы Ресслера.

Построим взаимную корреляционную функцию  двух хаотических радиоимпульсов, генерируемых системами Ресслера и различающихся параметром  и разными начальными условиями для модели генератора приемника и передатчика, описываемую соотношением (2).

,                                      (2)

где T – запаздывание.

Длина фрагментов реализации в каждой системе была взята равной 1000 отсчетов, что примерно соответствует 60 квазипериодам колебаний.

Типичный вид взаимной корреляционной функции представлен на рис. 5.

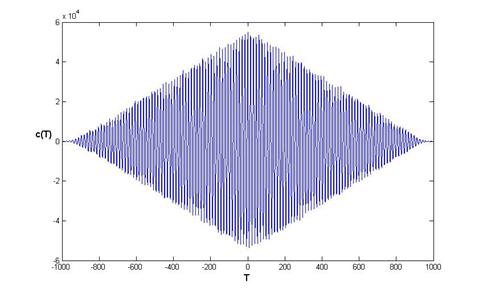
Рис. 5. Взаимная корреляционная функция двух хаотических сигналов,

генерируемая системой Рёсслера.

 

Из рисунка видно что, несмотря на различие начальных условий и разных значений одного из параметров , взаимная корреляционная функция спадает медленно и около максимума имеет вид функции, близкой к периодической. Ее затухание с увеличением  связано с тем, что при увеличении сдвига корреляция производится между линейно уменьшающимися длинами фрагментов. Для хаотических сигналов, генерируемых другими типами систем, это спадание может быть более быстрым, однако в любом случае амплитуда взаимной корреляционной функции на первых «периодах колебаний» примерно одинакова.

Отметим, что при построении взаимной корреляционной функции начальные условия в модели генератора передатчика и приемника берутся близкими к одинаковым. Это означает, что главный максимум взаимной корреляционной функции будет располагаться в точке нулевого сдвига между импульсами. При моделировании работы перемножителей, как было описано в предыдущем разделе, нулевой сдвиг выбирается для сигнала, поступающего из канала в первом перемножителе, а во втором перемножителе сигнал генератора сдвигается на величину равную примерно четверти «периода колебания» взаимной корреляционной функции.

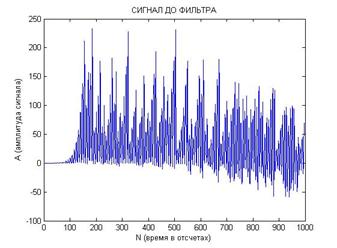
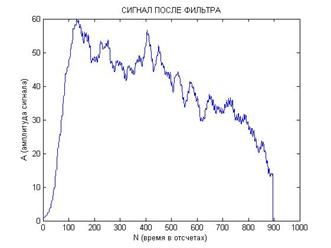
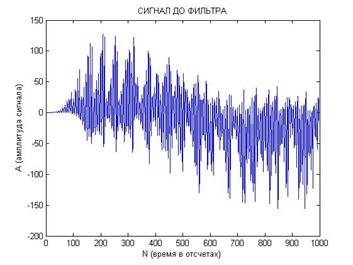
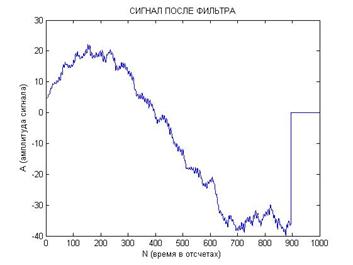
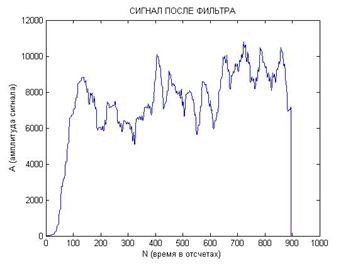
На рис. 6 представлена типичная реализация сигналов после перемножения в первом (а) и во втором (б) канале, а также после прохождения фильтра нижних частот в первом (в) и втором (г) канале.

 

а	в
б	г

Рис. 6. Реализация сигналов после перемножения (а и б) и после прохождения фильтра нижних частот (в и г) с близкими начальными условиями:

[x0; y0; z0]=[0,1; 0,1; 0,1] и [x0; y0; z0]=[0,1; 0,1; 0,2].

 

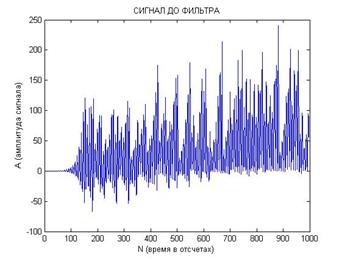
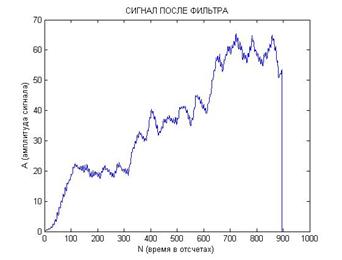
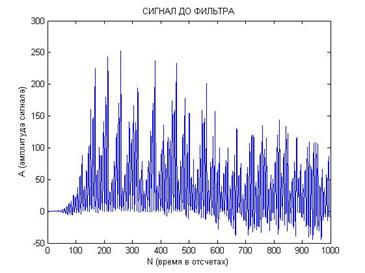
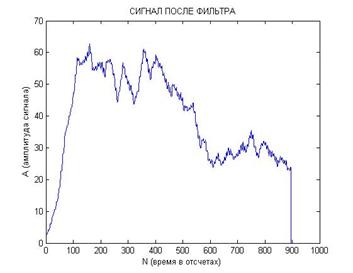
                          Теперь рассмотрим ситуацию, когда начальные условия для модели генератора в приемнике и передатчике хаоса сильно отличаются. Это будет соответствовать варианту построения системы, в которой в опорном генераторе хаоса приемника формируется непрерывный хаотический сигнал, а не хаотический радиоимпульс. Типичные результаты, моделирующие обработку принимаемого хаотического импульса в этом случае, показаны на Рис. 7.

 

а	в
б		г

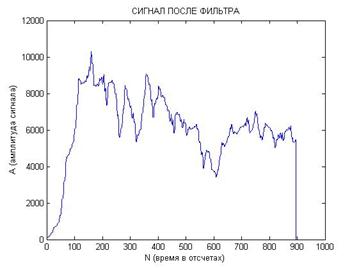
Рис. 7. Реализация сигналов после перемножения (а и б) и после прохождения фильтра нижних частот (в и г) с сильно различающимися начальными условиями:

[x0; y0; z0]=[0,1; 0,1; 0,1] и [x0; y0; z0]=[1; 1; 1].

 

Из рис. 7 видно, что также как и в случае с близкими начальными условиями предлагаемая схема приема надежно выделяет поступающие хаотические радиоимпульсы и отличает их от хаоса.

На рис. 8 показан сигнал на выходе сумматора для случая с примерно одинаковыми (а) и сильно различающимися (б) начальными условиями.

 

а

б

Рис. 8. Сигнал на выходе сумматора для случая с примерно одинаковыми (а) и сильно различающимися (б) начальными условиями.

                Выходной сигнал на рис. 8 соответствует появлению на входе приемника хаотического радиоимпульса. В случае если на входе приемника в момент перемножения находится нулевой сигнал (пауза) сигнал на выходе сумматора на том же промежутке времени будет равен нулю.

Выводы

В работе предложена новая схема некогерентного приема хаотических радиоимпульсов, использующая опорный генератор хаоса в приемнике. Проведены исследования этой схемы и показана ее способность приема хаотических радиоимпульсов. Хотя характеристики квадратичного приемника (использованного ранее) и нового приемника ожидаются примерно одинаковыми, новая структура приемника может иметь определенное преимущество за счет того, что в ней получение результата детектирования осуществляется за счет перемножения сигналов с большой и маленькой амплитудой, в то время как в ранее использованном приемнике (в приемнике с квадратичным детектором) фактически перемножаются два сигнала с малой амплитудой. Это обстоятельство позволяет либо совсем исключить предварительное усиление сигнала из приемника либо существенно уменьшить требования к коэффициенту предварительного усиления.

Литература

1.     Дмитриев А.С., Панас А.И., Старков С.О. Динамический хаос. Новые носители информации для систем связи. М.: Физматлит. 2002. 251с.

2.     Cuomo, K. & Oppenheim A. [1993] // “Circuit Implementation of Synchronized Chaos with Application to Communications,” Phys. Rev. Lett., 71, P. 65-68.

3.     Волковский А.Р., Рульков Н.В. Синхронный хаотический отклик нелинейной системы передачи информации с хаотической несущей // Письма в ЖТФ. 1993. Т. 19, вып. 3. С. 71-75.

4.     Dmitriev A.S., Panas A.I., Starkov S.O. Experiments on speech and music signals transmission using chaos // Int. J. of Bifurcation and chaos. 1995. V.5. №4. P. 1249-1254.

5.     Bohme F., Feldman U., Schwarz W., Bauer A. Information transmission by chaotizing // Proceedings of NDES’94. – Krakov, Poland. 1994. P. 163-168.

6.     Parlitz U., Chua L., Kosarev L., Halle K., Shang A. Transmission of digital signals by chaotic synchronization // Int. J. Bifurcation and Chaos. 1992. V. 2, № 4. P. 973-977.

7.     Бельский Ю.Л., Дмитриев А.С. Передача информации с помощью детерминированного хаоса // Радиотехника и электроника. 1993. Т. 38, №7. С. 1310-1315.

8.     Dedieu, H., Kennedy, M. P. & Hasler, M. [1993] “Chaos Shift Keying Modulation and Demodulation of a Chaotic Carrier Using Self-synchronizing Chua’s Circuits,” IEEE Trans. Circuits and Systems – 1 40, 634-642.

9.      Kennedy M. P. and Columban G. Chaotic Modulation for Robust Digital Communications over Multipath Channels. – Int. J. Bifurcation Chaos. – 2000. – V. 10. N 4. P. 695–719.

10.  Дмитриев А.С., Кяргинский Б.Е., Панас А.И., Старков С.О. Прямохаотические схемы передачи информации в сверхвысокочастотном диапазоне. – Радиотехника и электроника. 2001. Т. 46. № 2. С. 224–233.

11.  Дмитриев А.С., Кяргинский Б.Е., Максимов Н.А., Панас А. И., Старков С.О., Перпективы создания прямо хаотических систем связи в радио- и СВЧ-диапазонах // Радиотехника. 2000. №3. С. 9-20.

12.  Дмитриев А.С., Ефремова Е.В., Клецов А.В., Кузьмин Л.В., Лактюшкин А.М., Юркин В.Ю. Сверхширокополосная беспроводная связь и сенсорные сети // Радиотехника и электроника. 2008, Т. 53, №10, С. 1278-1289.

13.  802.15.4a-2007. IEEE Standard for Information Technology - Telecommunications and Information Exchange Between systems - Local and metropolitan area networks - specific requirement Part 15.4: Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications for Low-Rate Wireless Personal Area Networks (WPANs). N.Y.: IEEE, 2007. ieeexplore.ieee.org/servlet/opac?punumber=4299494.

14.  Мун Ф. Хаотические колебания М.: Мир. 1990. 311 с.