ПЯТИОСНАЯ РОБОТИЗИРОВАННАЯ ЛАЗЕРНАЯ СИСТЕМА И АЛГОРИТМ ЦИФРОВОЙ ОБРАБОТКИ ВЫХОДНЫХ ДАННЫХ ДЛЯ РЕГИСТРАЦИИ И МОРФОТОПОЛОГИЧЕСКОЙ ИДЕНТИФИКАЦИИ КЛЕТОЧНО-ТКАНЕВЫХ СТРУКТУР В ГИСТОМОРФОГЕНЕЗЕ
А. В. Нотченко 1,2, О. В. Градов 1,3
1Лаборатория нейронной структуры мозга НЦН РАМН
2МГТУ им. Баумана; 3Институт химической физики РАН
Получена 20 января 2012 г.
Аннотация. Реализована автоматизированная система морфолого-топологического определения фаз деления клеток и структурной дифференциации тканей в ходе морфогенеза, основанная на топологических свойствах клеточных культур, рассматриваемых в рамках наивной теории множеств. Элементарный роботизированный программно-аппаратный комплекс на базе микроскопа Zeiss с модифицированным предметным столиком и манипулятора Velleman модели KSR-1 позволяет управлять положением лазерного модуля, осуществляя угловое облучение образцов как в трансмиссионном, так и в темнопольном или люминесцентном режимах, и математическую обработку результатов регистрации. Данная низкобюджетная система может быть собрана и запрограммирована в условиях цитоморфологической или гистоморфологической лаборатории с использованием подручных средств. Программный код для обработки данных в MATLAB приводится в тексте статьи.
Ключевые слова: лазерная идентификация, топологический анализ, робот-манипулятор, одометрия, спекл, столик Федорова, цифровая обработка изображений, цифровая обработка сигналов, гистоморфогенез.
Abstract. An automated system for morpho-topological determination of cell division phases and structural differentiation of tissues during morphogenesis was implemented on the basis of topological properties of cell cultures, considered within the framework of set and manifold theories. A simple robotic hardware and software system based on Zeiss microscope with a modified stage and a Velleman manipulator KSR-1 allow to control the laser module position, carrying out the angular irradiation of samples either in transmission or in darkfield or luminescent modes and the subsequent mathematical data processing. This low-budget system can be easily assembled and programmed in any cytomorphological or histomorphological laboratory. The code for data processing in MATLAB is given at the end of the paper.
Keywords: laser identification, topological analysis, robo-arm, odometry, speckle, Feodorov stage, digital signal & image processing, hystomorphogenesis.
Топологические предпосылки.
Гетерогенные/гетерофазные среды, к которым относятся и клеточные культуры, при облучении их лазерным лучом формируют спекл-картины, состоящие из пятен – экстремумов яркости, адекватных структуре препарата (Рис.1,2). Поэтому топологическое строение спекл-текстур является критерием пролиферативной и дифференциационной активности клеточных структур. Это дает возможность изучать процессы пролиферации и морфогенеза в динамике, используя цейтраферную регистрацию спеклограмм препаратов или культур клеток. Критерием сравнения в таком случае будет связность-несвязность и топологическая эквивалентность (неэквивалентность) спеклов.
С топологических позиций
спекл-фотографии можно рассматривать как дискретные двумерные пространства, так
как они образованы группами изолированных точек. Если X – некоторое множество
точек спекла, а Z – семейство всех его подмножеств (дискретная топология спекл-структуры),
то пара (x, Z) - дискретное топологическое
пространство. В рамках процедуры бинаризации спеклограммы допустим, что
существует метрическое пространство c дискретной
метрикой ![]() ,
где
,
где
![]()
Это значит, что точка спеклограммы либо существует, либо не существует. Как следствие, минимальная единица спекл-структуры – точка (пятно) спеклограммы – является базой дискретной топологии. Очевидно, что распределение точек в пространстве характеризует морфо-топологические свойства исследуемой структуры.
При малом увеличении в
описываемом методе пятну на спекле соответствует клетка. В таком случае,
цейтраферные спеклограммы некоторой культуры до начала морфогенеза,
дифференциации и пролиферативно-цитокинетической активности клеток гомеоморфны
как пространства, имеющие одинаковую мощность - одинаковое количество элементов
(эквивалентного типа). Так культуры, регистрируемыми с малыми интервалами
времени, имеет место биективное отношение. Во времени происходит дрейф точек
подмножеств, при котором точки перемещаются во времени и пространстве, но не
меняют мощность множества в силу сохранения из количества, что эквивалентно ![]() .
.
В реальном пространстве – времени элементы множества X переходят в элементы множества Y, меняющего форму, но не мощность, что следует из отношения инъективности
![]() ,
,
причем очевидно, что любой элемент имеет свой прообраз как во времени – предыдущее состояние подмножеств, так и в пространстве – расположение точек меняется в зависимости от состояния прекурсора
![]() .
.
В результате этого меняются топологические характеристики структур спеклограмм, в частности, их связность как множеств. Спеклограммы могут иметь вид континуума, т.е. Хаусдорфова пространства. Это значит, что две точки x и y из X обладают непересекающимися окрестностями U(x), V(y) – зоной рассеяния. Это тождественно определению замкнутости диагонали в декартовом X х X - мерном квадрате:
![]() .
.
Можно показать, что
строки прогрессивной развертки матрицей ПЗС спеклограмм как топологических
объектов удовлетворяют условию линейно связного пространства. Если представить
строку развертки как отрезок числовой прямой ![]() с
соответствующей ему стандартной топологией, то пространство спеклограммы Х
с
соответствующей ему стандартной топологией, то пространство спеклограммы Х
![]() линейно связно, если для произвольных точек
линейно связно, если для произвольных точек ![]() имеется
непрерывное отображение
имеется
непрерывное отображение ![]() такое, что
такое, что ![]() При
этом топология
При
этом топология ![]() некоторого подмножества
некоторого подмножества ![]() является индуцированной
является индуцированной ![]() . Таким образом,
можно считать, что структуры спеклограмм культуры могут быть рассмотрены как
топологии, индуцированные путем отображения соответствующего вида. В силу этого
выполняется ещё одно необходимое условие изоморфизма – так как пространство X линейно связно, а
. Таким образом,
можно считать, что структуры спеклограмм культуры могут быть рассмотрены как
топологии, индуцированные путем отображения соответствующего вида. В силу этого
выполняется ещё одно необходимое условие изоморфизма – так как пространство X линейно связно, а ![]() , то гомотопические
группы
, то гомотопические
группы ![]() и
и ![]() изоморфны[1].
изоморфны[1].
Ситуация кардинально меняется в случае деления клеток. Если ограничивать спекл клетки окружностью, то можно видеть, что между состояниями спекла клетки в ходе её цитотомии/цитокинеза наблюдается бордизм (бордантность между окружностью и парой окружностей, в роли которых выступают соответственно исходная и дочерние клетки). В ходе клеточного цикла происходят ультраструктурные перестройки клетки, в связи с чем изменяется также и тонкая структура спекла. Таким образом, имеет смысл исследование тонкой структуры спеклограмм на предмет бордизмов структур, находящихся на пределе разрешения оптической системы в ходе цитотомии. Пример бордизма между состояниями до удвоения и по окончании удвоения спекла приведен на Рис.1.
Рис.1. Пример бордизма между спеклами в процессе деления.
Необходимо и возможно создание программно-аппаратного комплекса для точного определения принадлежности внутренних бордантных структур делящемуся бордантному спеклу (определением вложенности контура, то есть связности множества, ограниченного внешним контуром, исключающим находящиеся во вложенном контуре точки), а также установления бордизмов и топологических неэквивалентностей, адекватных цитокинезу и дифференциации соответственно.
Материалы и методы.
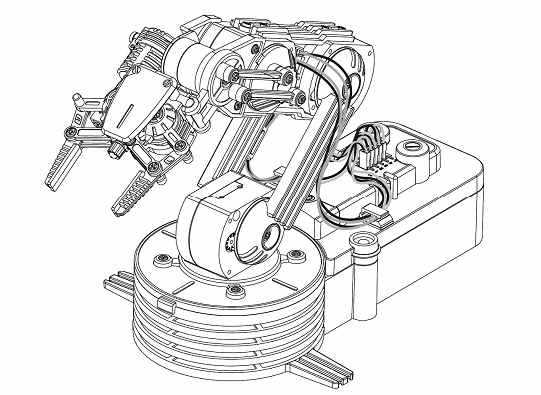
Технологически доступна малобюджетная реализация данной системы, состоящая из тринокуляра с цифровой цейтраферной камерой и пятиосным столиком Федорова вместо штатного двухкоординатного или вращающегося центрируемого, и электромеханической системы управления положением лазерного источника[2]. В описываемой реализации были использованы база и шасси микроскопа Zeiss и модифицированный вращающийся столик типа UD-124 (рис.2). В качестве малогабаритных источников излучения использовались лазеры на основе полупроводниковых гетероструктур (диодные гетеролазеры) и лазерные модули производства "Royal Tech", "Sean & Stephen" и "Honeywell" с длинами волн 405, 532, 635, 645, 650, 660, 670, 850 нм. Перемещение излучателей относительно препарата в пространстве осуществлялось с помощью робота-манипулятора Velleman KSR-1 (рис.3). Углы и режимы сканирования задавались с помощью специализированной программы и фиксировались к соответствующим кадрам цейтраферной съемки путем автоматического протоколирования. Изображения фиксировались камерой Canon и сохранялись в формате RAW и JPEG, что позволяло извлекать спектрозональную информацию в диапазонах длин волн, соответствовавших использовавшимся источникам. Для извлечения информации по спектрозональному распределению на спеклах использовалась система AM Lab Hesperus. Топологическая обработка информации производилась в системе MATLAB с помощью алгоритма, реализованного в Graph_Speckle_Analyzer v. 2 β (автор А.В.Нотченко).
Рис.2. Вращающийся Федоровский столик позволяет размещать культуры под разными углами и, при наличии автоматического управления вращением, использовать его в ходе долгосрочного спекл-мониторинга как шейкер-ротатор для культивируемой культуры.
Рис.3. Манипулятор для управления положением лазерного источника.
Данный алгоритм способен определить вложенность одного контура в другой, т.е определить связность некоторого множества, ограниченного внешним контуром, но исключающим находящиеся во вложенном контуре точки. Метод проверки заключается в определении принадлежности точек внутреннего контура множеству ограниченному внешним контуром через его характеристическую функцию.
Последовательность точек
в обходе контура по часовой стрелке ![]() и представление каждой точки в 2-мерной
декартовой прямоугольной система координат
и представление каждой точки в 2-мерной
декартовой прямоугольной система координат ![]() являются основной структурой данных на входе алгоритма.
Функция проверки выпуклости множества М определяется через последовательную
проверку наличия точек в выделенных полуплоскостях, построенных на основе двух
предыдущих точек и соглашении о перечисления точек по часовой стрелке.
являются основной структурой данных на входе алгоритма.
Функция проверки выпуклости множества М определяется через последовательную
проверку наличия точек в выделенных полуплоскостях, построенных на основе двух
предыдущих точек и соглашении о перечисления точек по часовой стрелке.
Граница полуплоскости
определяется как линия между двумя точками, например линия ![]() образована точками
образована точками ![]() и
и![]() , а выбор полуплоскости относительно
разделяющей линии определяется через квадрант, в котором находится вторая точка
относительно первой (см., напр., рис. 4).
, а выбор полуплоскости относительно
разделяющей линии определяется через квадрант, в котором находится вторая точка
относительно первой (см., напр., рис. 4).
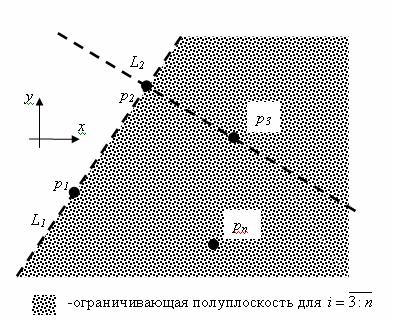
Рис.4. Пояснение к принципу работы алгоритма Graph_Speckle_Analyzer.
Так, например для точек ![]() и
и![]() , где
, где ![]() находится в первом квадранте если считать
находится в первом квадранте если считать ![]() точкой начала
координат, поэтому следуя соглашению о последовательности точек выделяется
правая полуплоскость.
точкой начала
координат, поэтому следуя соглашению о последовательности точек выделяется
правая полуплоскость.
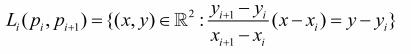 (0.1)
(0.1)
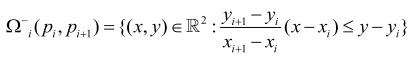 (0.2)
(0.2)
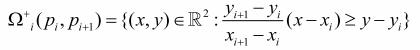 (0.3)
(0.3)
Полуплоскость ![]() - выбирается, когда точка
- выбирается, когда точка ![]() находится в 1-м или 4-м
квадранте
находится в 1-м или 4-м
квадранте ![]() ,
, ![]() - если 2-м или 3-м.
Поэтому характеристическая функция для выпуклого многоугольника будет выглядеть
как:
- если 2-м или 3-м.
Поэтому характеристическая функция для выпуклого многоугольника будет выглядеть
как:
![]() (0.4)
(0.4)
Алгоритм при фиксации выделенного многоугольника, сохраняет его в конечной структуре данных в виде матриц для описания неравенства задающего многоугольник:
![]() ,
(0.5)
,
(0.5)
где ![]() -
множество матриц размерности
-
множество матриц размерности ![]() .
.
Основной алгоритм выделяет из последовательности вершин те подмножества, которые образуют выпуклые множества и таким образом через конечное число итераций удаляют из множества все точки за исключением 2-х последних, и в этот момент срабатывает условие выхода из цикла “while”. На выходе производится сборка всех характеристических функций выпуклых многоугольников через операцию дизъюнкции.
![]() (0.6)
(0.6)
На выходе получаем характеристическую функцию невыпуклого многоугольника. Проверка на наличие в нем точек вложенного контура производится в цикле. Блок-схема алгоритма в формате ERD[3] приведена на илл. 5.
Полный текст программы Graph_Speckle_Analyzer для компиляции при изготовлении системы, аналогичной описываемой в настоящей статье, в приведен в приложении 1. При его использовании следует учитывать совместимость версий MATLAB; для изготовления данного кода использовалась относительно новая версия 7.9.0 (R2009b). Проверка ПО на совместимость с другими версиями не производилась.
К вопросу о применимости спекл-топологического подхода.
Существуют различные оптико-топологические процессы[4], применимые в интерференционных, в частности, спекл-интерферометрических методах измерений (Auclair-Fortier M.-F. et al., 2002; Dennis M.R., 2003, 2008, 2009; Berry M.V., 2007; Flossman F., 2008; O'Holleran K., 2006, 2009). Вместе с тем, известны проективно-морфологические методы сопоставления и анализа морфологических операторов, на базе структурных элементов - функций, а также структурирующих параметров и критериев - функционалов. Сравнение образа с моделью через оператор проекции в рассматриваемом случае производится путём определения морфологического коэффициента корреляции.
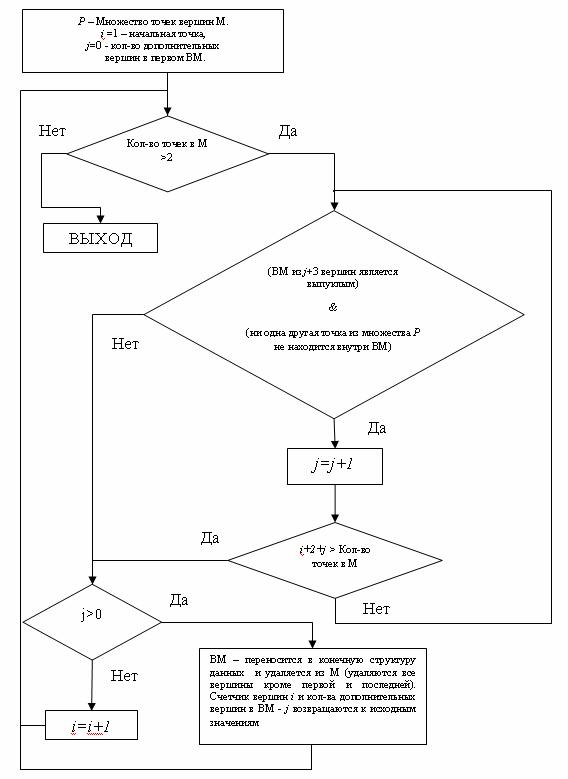
Рис.5. Блок-схема алгоритма программы Graph_Speckle_Analyzer.
Таким образом, спеклограммы культур, по крайней мере, для эксплантных, органных и органотипических типов культур, могут являться не только критерием пролиферативно-дифференциационной активности и фаз клеточного цикла, но и объектом проективно-морфологического сличения. Отличная ситуация в диссоциированных клеточных культурах связана с высокой стохастичностью паттернов во времени. Нестационарный характер границ контуров биологических культур во времени препятствует точному идентификационному сличению по маске, вследствие чего неизбежным является применение косвенных топологических методов анализа.
Пример анализа спеклограммы культуры.
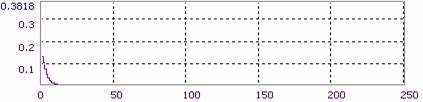
На Рис.6 приведена микрофотография интерференционной спекл-картины, снятой с модельной культуры клеток. Различимы пятна, характеризующиеся градиентом яркости к фону, соответствующие клеткам. Данная микрофотография снята при облучении объекта красным лазером (λ = 650 нм), в связи с чем возможно выделить относительно неширокий спектрозональный диапазон, соответствующий распределению когерентного источника. В таком случае можно будет по спектрозональной гистограмме идентифицировать периоды спекл-текстуры, зависящие, в частности, от оптических свойств поверхности (межфазной границы), культуры клеток.
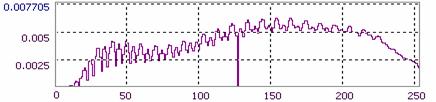
Спектрозональное разложение данной микрофотографии дано на Рис.7: можно видеть, что не входящие в заданный диапазон каналы (зеленый и синий - G и B) характеризуются быстрым экспоненциальным затуханием и отсутствием сигнала на оставшемся фрагменте оси абсцисс, в то время как красный канал имеет выраженный квазипериодический характер гистограммы сигнала (R). Таким образом можно изучать, в частности, распределение лазерно-индуцированной флуоресценции в препарате культуры ex vivo с использованием витальных красителей. Исходя из распределения интенсивности по каналам делается вывод о необходимости использования сигнала монохроматического канала R (полученного в виде rdp-файла системы AM Lab Hesperus) для топологического анализа.


а б
Рис.6. Пример расшифровки спекл-микрофотографии культуры клеток в ПО Graph_Speckle_Analyzer (а) и окно трехканальной спектрозональной установки Contourplot parameters (б).
 R
R
 G
G
 B
B
Рис.7. Пример спектрозонального разложения спеклограммы культуры.
Запустим из среды MATLAB 7.9.0 графический интерфейс пользователя (GUI) программы Graph_Speckle_Analyzer. Загрузим спекл-изображение. С помощью цифрового трансфокатора (пиктограммы луп на графическом интерфейсе) найдём интересующий нас фрагмент спеклограммы. Нажатием кнопки А построим карту экстинкционного градиента образца и автоматически опознаем контуры границ двух объектов, которыми могут быть различные клетки или клетка и элемент спекла её микроструктуры (и т.д.). Для этого, по указаниям программы, отображающимся в нижней части окна, последовательно укажем уровни на градиентной карте, соответствующие контурам идентифицируемых объектов (в программе предусмотрено иерархическое различение двух объектов, один из которых, по умолчанию, рассматривается как множество, а другой как входящее в него подмножество или не принадлежащее и не автоморфное ему множество). В результате программа выдаст запись в нижней части окна "красный контур (...M1...) не вложен в зелёный (...M2...)" или, наоборот, "красный контур (...M1...) вложен в зелёный (...M2...)", где M1 и М2 - площади и периметры избранных контуров. Аналогичные сообщения получаются и в ручном режиме (запускается клавишей М), за тем исключением, что площади и периметры определяются ручной установкой границ контуров многоугольника по точкам, заданным пользователем.
Целесообразность использования канала того спектрозонального диапазона, которым производилось облучение, объясняется структурой алгоритма, требующей в специальном окне ввода весовых коэффициентов каналов при выборе автоматического распознавания (см. илл. 6). Возможен анализ и без спектрозонального разложения: как следует из илл. 7, интенсивность сигнала в PDF-сетке на доминирующем канале имеет порядковое различие по отношению к другим каналам. Несмотря на это, при наличии спектрозональных помех машинное время, требуемое на анализ спеклограммы увеличивается, точность выделения контуров падает. Тем не менее, при затрате значительных машинных ресурсов измерения производятся верно. Топологическая функция программы реализуется для неспециалиста-биолога в виде указания на вложенность или отсутствие вложения контуров, тогда как для полноценного топологического анализа достаточно заменить в тексте программы элемент "красный контур" на наименование множества M1, "зеленый контур" на наименование М2, "вложен" и "не вложен" на математические знаки принадлежности или непринадлежности (Î,Ï, Í, Ì, Ê, É) соответственно. Это отразится в окне Graph_Speckle_Analyzer в нижней части окна (илл. 8) при индикации результатов топологического анализа.
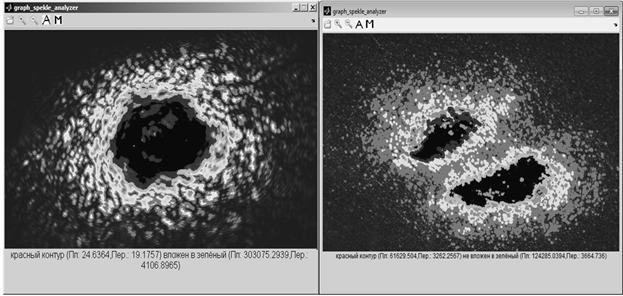
Рис.8. Топологический анализ одиночного и удваивающегося спеклов. Индицируется вложенность контуров в одиночном и непринадлежность множеств в удвоенном пучке с помощью Graph_Speckle_Analyzer.
Специальные вопросы спекл-топологического подхода к анализу связности клеточно-тканевых структур.
На Рис.8 приведены примеры индикации вложенности для одиночных спекл-пятен[5], однако же в реальных культурах клеток могут возникнуть трудности с непосредственным различением клеток и субклеточных структур - вторичных источников спекл-пятен. Так, в частности, за счет интерференционных явлений, могут диффузно размываться граничные контуры множеств единичных клеток. Произведем качественные измерения спекл-пятен с культуры клеток в приближении сферических вторичных источников (сферопластов), для чего используем метод видеогранулометрии (Blot G., 1987; Primel L., Tourenq C., 1990) как цейтраферную модификацию метода фотогранулометрии, использовавшейся Хассом для океанологических исследований (Hass H.C., 1993). Используем модификацию и алгоритм, наиболее близкие к биологическим направлениям исследований (Kozinets G. et al., 1998; Medovyi V.S. et al., 2006). Результаты гранулометрии фрагмента флуктуирующей спекл-текстуры с рефлексами от отдельных клеток, показанных на илл. 6, приведены на илл. 9.

Рис.9. Гранулометрия с автоматическим распознаванием
границ окружностей (сфер в двумерной проекции) во времени по статистически вероятным зонам экспонирования.
Пример трехмерной реконструкции опознанных таким образом групп сфероцитов дан на Рис.10. Очевидно, что при опознании микросфер программное обеспечение "видит" их наложения друг на друга и частичное перекрытие спекл-пятен, что может соответствовать реальной картине адгезии клеток или быть артефактом случайных воздействий. При статистической достоверности результата, детерминируемой и характеризуемой временем стабильной регистрации указанных структур в ходе экспозиции покадрово-цейтраферных выборок или в режиме накопления сигнала, вероятнее первое.

Рис.10. Определение распределения агрегирующих сфероцитов в пространстве методом лазерного топологического спекл-анализа с визуализацией по Эйлеру - Венну. Этот метод можно, в частности, использовать для изучения агрегации форменных элементов крови.
В таком случае, наложения условных окружностей, отграничивающих множества клеток, можно рассматривать как диаграммы Венна в теории множеств. В зависимости от местонахождения максимальной оптической плотности денситограммы негатива спекла или, что эквивалентно, яркостных максимумов спеклограммы, можно дифференцировать, в частности:
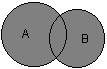
1. диаграммы Венна для объединения двух множеств - когда происходит точное машинно-неразличимое слияние (агрегация/адгезия или цитотомия на пределе разрешения микроскопа, что индицирует фазу клеточного цикла) двух клеток, включая промежуток между ними:
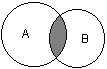
2. диаграммы Венна для пересечения двух множеств - когда в силу интенсивных диффузных процессов экстремумом является область пересечения клеточных гранулометрических спекл-контуров:
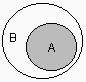
3. диаграммы Венна для отношения включения множеств - когда компартмент какого либо состава, содержимое вакуоли или окрашенная специфическим флуорохромом ядерная область является источником высокой яркости или же сильно пропускающей излучение[6] (при контровом расположении излучателя)
4. диаграммы Венна для отношения вычитания, способные характеризовать, в частности, фагоцитарную активность в культуре, так как круги Эйлера клеток обладают друг по отношению к другу свойством А \ В = {х | х Î А и х Ï В}:
![]()
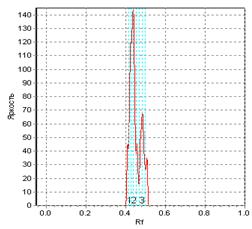
Таким образом, расшифровка динамической структуры цитологических спеклограмм с позиций топологии и теории множеств может рассматриваться как метод установления функционально-морфологической и морфофизиологической популяционной активности в культурах клеток во времени, и, в конченом итоге, как индикатор трендов конкурентного, структурно-дифференциального и морфогенетического плана в её культивации. Методами прецизионной физиологической и аналитической морфобиохимической видеоденситометрии (Silverman N.R., 1972; Kramer J. et al., 1980) можно рассмотреть локомоторную динамику, ведущую к формированию сложных спекл-текстур, интерпретируя её с позиций вискозиметрического "тестирования" среды движущейся клеткой. Тогда задача о передвижении клетки в тренде морфогенеза будет тождественна хроматографической задаче о передвижении стартового пятна в подвижной фазе - растворителе. Отношение расстояния, пройденного пятном, к расстоянию, пройденному растворителем стандартно обозначается Rf. Возможно принять систему координат, в которой растворитель является стационарной фазой, и измерять ток и скорость непосредственно движущегося пятна. Будучи неприменим в хроматографии в связи с капиллярно-химическими и диффузионными эффектами элюента, данный подход вполне оправдал бы себя при анализе цитокинетической и локомоторной динамики клеток в культуре. Нами (вследствие цейтраферного метода регистрации культуральных спеклов) использовалась методика обработки, заимствованная из "четырёхмерной" хроматографии (Berezkin V.G., 2009) с расширенными возможностями анализа изображений. Измерения эквивалента отношения Rf для сферопластов в спеклографируемой культуре производили с помощью видеоденситометра "Sorbfil TLC" при автоматическом расчете характеристик треков (имеющих в рамках топологической интерпретации спеклограмм смысл множеств и пространств, дефинированный в разделе "Топологические предпосылки"). Результаты измерений приведены на Рис.11(а, б): можно видеть, что, в силу того, что культура есть топологическое множество клеток, в распределении Rf спеклограммы данного множества (б) можно распознать множество Rf единичных клеточно-сопряженных спеклограмм (а). Это очевидно, так как, с позиций двухтиповой теории множеств, клетка, идентификация которой происходит по спеклу, не являясь отдельным подмножеством клеток-источников пространственной модуляции спеклов, является, однако же, его урэлементом. Используя построчное построение паттерна спекла, аналогично методам цифровой идентификации в автоматизированной хроматографии, можно добиться не только вычисления параметров качественного распределения клеток по спеклограмме, но и реализовать автоматический фингерпринтинг - органотипическую или видоспецифичную идентификацию культур (по библиотекам подгружаемых и индексируемых в ходе обучения программы образов - см., напр., для ср., сб. п/ред. Wagner et al., 2011). Для этого можно использовать маскирующие сравнительные элементы, репрезентирующие модель наложения диаграмм Венна на базе структур, отличных от кругов Эйлера, получаемых при гранулометрии и пригодных лишь для сферических или условно сферических клеточных стуктур.

а б
Рис.11. Графики зависимости яркости точки от фактора распределения; а - одиночное спекл-пятно, которое можно сопоставить одиночной клетке-источнику, б - спеклограмма культуры клеток при малом микроскопическом увеличении.
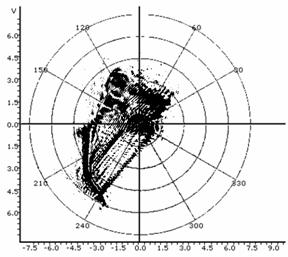
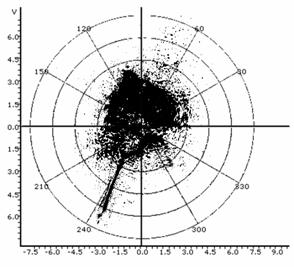
Проблемы оптимального формирования топологии спекла образца.
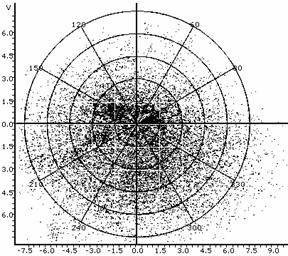
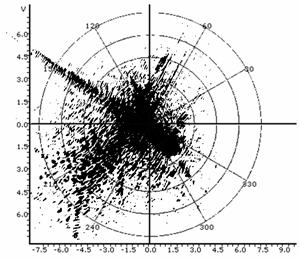
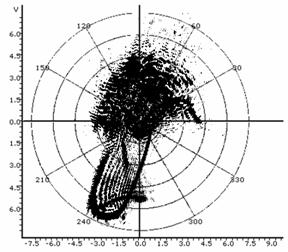
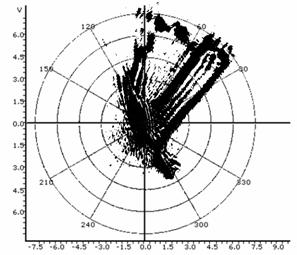
Используя оптико-геометрические построения (Tyc T. et al., 2011) можно выдвинуть предположение о возможности искажения топологических характеристик спеклограммы культуры, биологического / биомиметического идентифицируемого указанным путем образца, определяемой свойствами объектива или мениска культивационной среды. Так, в частности, возможно возникновение петель как топологических неэквивалентностей или, что точнее, топологически неинвариантных, не гомеоморфных друг другу спеклограмм. В ряде оптически-неоднородных культур это может приводить к сложным топологическим эффектам обусловленным интерференционно-рефракционными процессами в оптическом тракте культуры (включая иммерсионные эффекты и двойное лучепреломление клеток). В качестве примера можно привести искажения спеклов, возникающие за счет объективных эффектов, приведенные в таблице 1. Данные изображения ("диаграммы направленности") были получены при центровке точки источника в центре системы полярных координат с помощью утилиты FindGraph v. 1.892 (Uni. Phis. Lab.). Можно видеть, что, по отношению к обычному гауссовому распределению пучка все обусловленные цитоморфологическими образованиями структуры являются возмущением (модуляцией) спекл-поля; вместе с тем, любые возмущения могут переходить друг в друга при соответствующем изменении типа среды распространения сигнала или оптического тракта регистрирующей системы. Так, в таблице 1 нижние 4 примера можно рассматривать как диффеоморные отображения друг друга с переходом в пределе через сингулярность петли к не гомеоморфному (не взаимно однозначному) отображению, меняющему топологические свойства структуры. Другими словами, топологические характеристики спеклограммы культуры могут быть продуктом не только самой культуры, но и топологии оптического эксперимента, что накладывает весомые ограничения на методики и протоколирование спекл-топологических измерений и их интерпретацию. В описанном программно-аппаратном комплексе протоколирование угловых перемещений источника, как указывалось выше, производится автоматически.
Таблица 1: Типичные искажения топологии спеклограмм в лазерном топологическом спекл-анализаторе пролиферативной и дифференциационной активности культур.
|
|
|
|
Обычное диффузное распределение спекла, характерное для дисперсных систем. |
Рефракционный эффект: отражение пучка под углом от грани счетной камеры. |
|
|
|
|
Интерференция на объективе или мениске приводит к образованию петель. |
Перенаправление петли вращением образца или изменением положения к объективу. |
|
|
|
|
Сочетание граничных рефракционных эффектов и деформированной ими петли. |
Сингулярный случай вырождения петли до состояния углового рефлекса пучка. |
Заключение.
Созданный программно-аппаратный комплекс может быть воспроизведен простыми средствами в любой цитоморфологической / гистоморфологической лаборатории. Эффект от внедрения топологической морфометрии в практику очевиден. Цена использованных составляющих конструкции, исключая микроскоп, который может быть произвольным, и стабилизированный лабораторный блок питания, необходимый для иллюминации столика Федорова и культур на нем, пренебрежительно мала: цена манипулятора Velleman KSR-10 в европейских ценах колеблется от 60€ до 70€, лазерные модули (для работы не требуется иметь полный набор спектральных источников - достаточно иметь три, соответствующих различным спектрозональным каналам RGB; комплектация установки лазерными диодами производится в соответствии со спектральными характеристиками исследуемого объекта) - от 20€ до 100€, программное обеспечение и плата для USB-подключения манипулятора - от 35€ до 50€[7]. Открытый программный код топологического анализатора, приведенный в приложении, и возможность адаптации кода при установке MATLAB под Linux (нами апробирована установка под Scientific Linux разработки CERN / Fermilab) делают данную систему корректным общедоступным заменителем проточной цитометрии и цитофлуориметрии с расширенными возможностями детектирования, используемых для классификации клеток с возможностью выявления клеточных субпопуляций и анализа клеточного цикла.
Литература
I. Computational Algebraic Topology Approach for Optical Flow /M.-F. Auclair-Fortier, P. Poulin, D. Ziou, G.D. De Moivre, U. De Sherbrooke, M.A. Allili // Pattern Recognition, Proc. 16th ICPR - 2002. - Vol. I - pp. 352 – 355.
II. Berezkin V.G. Four-dimensional thin-layer chromatography / V. G. Berezkin, S. S. Khrebtova, N. Yu. Kulakova // Dok. Phys. Chem. - 2009 - Vol. 429. - No. 1. - pp. 229-232.
III. Berry M.V. Topological events on wave dislocation lines: birth and death of loops, and reconnection / M.V. Berry, M.R. Dennis //, Journal of Physics A: Mathematical and Theoretical. - 2007. - Vol. 40. - pp. 65-74.
IV. Blot G. Automatisation de l'analyse granulometrique. Presenation d'un nouveau capteur de formes, le videogranulometrie (Réf. ATILH n°24143) / G. Blot // Rev. Gen. des Rout. et Aer. - 1987. - Vol. 61. - No. 639. - pp. 39-43.
V. Dennis M.R. Correlations and screening of topological charges in Gaussian random fields/ M.R. Dennis // Journal of Physics A: Mathematical and General. - 2003. - Vol. 36. - pp. 6611-6628
VI. Dennis M.R. Superoscillation in speckle patterns / M.R. Dennis, A.C. Hamilton, J. Courtial // Optics Letters. - 2008. - Vol. 33. - pp. 2976-2978.
VII. Dennis M.R. Topological configurations of optical phase singularities / M.R. Dennis // Topologica - 2009. - Vol. 2. - pp. 007-1 - 007-10.
VIII. Flossmann F. Polarization singularities in 2D and 3D speckle fields / F. Flossmann, K. O'Holleran, M.R. Dennis, M.J. Padgett // Physical Review Letters. - 2008. - Vol. 100. - pp. 203902-1 - 203902-4.
IX. Hass H.C. Deposition processes under changing climate: Upper Subatlantic granulometric records from the Skagerrak (NE-North Sea) / H.C. Hass // Marine Geology. - 1993. - Vol. 111. - pp. 361 - 378.
X. O'Holleran K. Topology of optical vortex lines formed by the interference of three, four, and five plane waves / K. O'Holleran, M.J. Padgett, M.R. Dennis // Optics Express. - 2006. - Vol. 14. - pp. 3039-3044.
XI. O'Holleran K. Topology of light's darkness / K. O'Holleran, M.R. Dennis, M.J. Padgett // Physical Review Letters. - 2009 - Vol. 102. - p. 143902-1 - 143902-4.
XII. Kozinets G. MECOS-C: return to image analysis in microscope examination of blood smears. / G. Kozinets, V. Medovy, A. Pyatnitsky, B. Sokolynsky, A. Gusev // Proc. SPIE “Optical Diagnostic of Living Cell 2”. - 1998. - Vol. 3. - p.260
XIII. Kramer J. Quantitative evaluation of gel electrophoretic patterns by videodensitometry / J. Kramer, N.B. Gusev, P. Friedrich // Anal. Biochem. - 1980. - Vol. 102. - Issue 2. - pp. 295 - 298.
XIV. Medovyi V.S. An automated microscopy system MECOS-C2 and its trials. / V.S. Medovyi, A.A. Parpara, A.M. Pyatnitskii, B.Z. Sokilinskii, V.L. Dem'yanov // Biomedical Engineering. - 2006. - No. 4. - pp. 197-202.
XV. Silverman N.R. Clinical Video-Densitometry, Pulmonary Ventilation Analysis / N.R. Silverman // Radiology. - 1972. - Vol. 103. - pp. 263-265.
XVI. Soponar F. Quantitative Evaluation of Paracetamol and Caffeine from Pharmaceutical Preparations Using Image Analysis and RP-TLC / F.Soponar, A.C. Mot, C. Sarbu // Chromatographia. - 2009. - Vol. 69. - No. 1-2. - pp. 151-155.
XVII. Absolute instruments and perfect imaging in geometrical optics / T. Tyc, L. Herzanova, M. Sarbort, K. Bering // New Journal of Physics. - 2011. - Vol. 13. - art.115004. - 23pp.
XVIII. Vizilter Y.V. Projective morphologies and their application in structural analysis of digital images / Y.V. Vizilter, S.Y. Zheltov // Journal of Computer and Systems Sciences International. - 2008. - Vol. 47. - No. 6. - pp. 944-958.
XIX. Vizilter Y.V. The use of projective morphologies for object detection and identification in images / Y.V. Vizilter, S.Y. Zheltov // Journal of Computer and Systems Sciences International. - 2009. - Vol. 48. - No. 2. - pp. 282-294.
XX. Vizilter Y.V. Design of data segmentation and data compression operators based on projective morphological decompositions / Y.V. Vizilter // Journal of Computer and Systems Sciences International. - 2009. - Vol. 48. - No. 3. - pp. 415-429.
XXI. Vizilter Y.V. Skeleton-based morphological shape comparison / Y.V. Vizilter, S. V. Sidyakin, A.Y. Rubis, V. Gorbatsevich // Pattern Recognition and Image Analysis. - 2011. - Vol. 21. - No. 2. - pp. 357-360.
XXII. Chromatographic Fingerprint Analysis of Herbal Medicines / Eds.: H. Wagner, R. Bauer, D. Melchart, P.-G. Xiao, A. Staudinger // Springer, 2011 - 1064 p.
XXIII. Primel L., Tourenq C. Granulats, Presses de l'Ecole Nationale des Ponts et Chauess, 1990 (Eng. trans.: Primel L. Aggregates: geology, prospection, environment, testing, specifications, extraction, processing plants, equipments, quality control / L. Primel, C. Tourenq // Taylor & Francis. - 2000 - 590 p.).
Приложение 1: Листинг Graph_Speckle_Analyzer для MATLAB.
function varargout = graph_spekle_analyzer(varargin)
% GRAPH_SPEKLE_ANALYZER M-file for graph_spekle_analyzer.fig
% Last Modified by GUIDE v2.5 06-Aug-2011 08:48:05
% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name', mfilename, ...
'gui_Singleton', gui_Singleton, ...
'gui_OpeningFcn', @graph_spekle_analyzer_OpeningFcn, ...
'gui_OutputFcn', @graph_spekle_analyzer_OutputFcn, ...
'gui_LayoutFcn', [] , ...
'gui_Callback', []);
if nargin && ischar(varargin{1})
gui_State.gui_Callback = str2func(varargin{1});
end
if nargout
[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
gui_mainfcn(gui_State, varargin{:});
end
end
% End initialization code - DO NOT EDIT
% --- Executes just before graph_spekle_analyzer is made visible.
function graph_spekle_analyzer_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% varargin command line arguments to graph_spekle_analyzer (see VARARGIN)
% Choose default command line output for graph_spekle_analyzer
handles.output = hObject;
% Update handles structure
guidata(hObject, handles);
set(handles.mainaxes,'ticklength',[0 0],'xticklabel',[],'xticklabelmode','manual','yticklabel'...
,[],'yticklabelmode','manual','units','normalized','nextplot','add');
set(handles.maintext,'fontsize',12);
firsttext='A - автоматическое выделение контура М - ручное выделение контура';
set(handles.maintext,'String',firsttext);
global imag
imag=[];
end
% --- Outputs from this function are returned to the command line.
function varargout = graph_spekle_analyzer_OutputFcn(hObject, eventdata, handles)
% varargout cell array for returning output args (see VARARGOUT);
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% Get default command line output from handles structure
varargout{1} = handles.output;
end
% --------------------------------------------------------------------
function uitb_open_ClickedCallback(hObject, eventdata, handles)
global imag
[filename, pathname]=uigetfile({'*.jpg;*.tif;*.png;*.gif','All Image Files';'*.*','All Files' });
imag=imread( fullfile(pathname, filename));
%imag=imread('d:\flash_backup_03052011\micro\example\Image5.tif');
if isempty(imag)
errordlg('Image wasn''t loaded, try again.');
return
end
delete(allchild(handles.mainaxes));
[imheight,imwidth,~]=size(imag);
imhan=image(imag,'parent',handles.mainaxes);
set(imhan,'userdata',imag);
set(handles.mainaxes,'ticklength',[0 0],'xticklabel',[],'xticklabelmode','manual','yticklabel'...
,[],'yticklabelmode','manual','units','normalized','xlim',[0 imwidth],'ylim',[0 imheight]);
alch=allchild(handles.mainaxes);
for i=1:length(alch)
set(alch(i),'hittest','off');
end
end
% ------------------------------------------------------------------
function uipt_auto_ClickedCallback(hObject, eventdata, handles)
%pic=get(findobj(handles.mainaxes,'type','image'),'userdata');
global imag
if isempty(imag)
errordlg('You must select picture!');
return
end
%------------------------------------------------------------------
prompt = {'Red chanel coefficient:','Green chanel coefficient:',...
'Blue chanel coefficient:','Number of slices:','Contour linewidth:'};
dlg_title = 'Contourplot parameters';
num_lines = 1;
def = {'0.4','0.6','0.4','1','2'};
answer = inputdlg(prompt,dlg_title,num_lines,def);
I = str2double(answer(1))*imag(:,:,1)+str2double(answer(2))...
*imag(:,:,2)+str2double(answer(3))*imag(:,:,3);
delete(allchild(handles.mainaxes));
imagesc(max(max(I))-I);hold on;
n_sli=str2double(answer(4));
l_wid=str2double(answer(5));
[conar,conhand]=imcontour(I,n_sli); hold off;
set(findobj('type','hggroup'),'linewidth',l_wid);
set(handles.mainaxes,'xticklabel',[],'yticklabel',[],'Ticklength',[0 0],...
'ButtonDownFcn',@SelCon);%,'xlim',get(handles.imag_axes,'xlim')...
%,'ylim',get(handles.imag_axes,'ylim'));
achpa=allchild(handles.mainaxes);
for i=achpa
set(i,'hittest','off');
end
firsttext='Выделете первый контур (кликните на контур)';
set(handles.maintext,'String',firsttext);
end
% ------------------------------------------------------------------
function SelCon(mainaxes,~)
cp=get(mainaxes,'currentpoint');
cp=cp(1,1:2)';
chlist=allchild(findobj(mainaxes,'type','hggroup'));
mincon=cell(size(chlist));
mindist=zeros(size(chlist));
for i=1:length(chlist)
mincon{i}=[get(chlist(i),'xdata')';get(chlist(i),'ydata')'];
%mindist(i)=min(min(abs(mincon{i}-cp*ones(1,length(mincon{i})))));
mindist(i)=min(sum((mincon{i}-cp*ones(1,length(mincon{i}))).^2,1));
end
mini=find(mindist==min(mindist));
if isempty(findobj(mainaxes,'userdata','click'))
set(chlist(mini(1)),'userdata','click');
hold on;
plot(mincon{mini(1)}(1,:),mincon{mini(1)}(2,:),'linewidth',3,...
'color',[0 1 0],'parent',mainaxes);
hold off;
firsttext='Выделите второй контур (кликните на контур)';
set(findobj('tag','maintext'),'String',firsttext);
else
per=@(p)sum(sqrt(sum(([p(:,2:end) p(:,1)]-p).^2,1)));
hold on;
plot(mincon{mini(1)}(1,:),mincon{mini(1)}(2,:),'linewidth',3,...
'color',[1 0 0],'parent',mainaxes);
hold off;
%set(chlist(mini(1)),'userdata','second_click');
p=[get(chlist(mini(1)),'xdata')';get(chlist(mini(1)),'ydata')'];
co=findobj(mainaxes,'userdata','click');
ps=[get(co,'xdata')';get(co,'ydata')'];
ps=flipdim(ps(:,1:end-2),2);
p=flipdim(p(:,1:end-2),2);
%----------------------------------------------------------------
poly=discrip(ps);
verd=true;
for j=1:size(p,2)
if ~poly(p(:,j))
verd=false;
break
end
nntext=['красный контур (Пл: ',num2str(polyarea(p(1,:),p(2,:))),...
',Пер.: ' num2str(per(p)) ') вложен в зелёный (Пл: ',...
num2str(polyarea(ps(1,:),ps(2,:))),',Пер.: ',num2str(per(ps)) ')'];
set(findobj('style','text'),'string',nntext);
end
if ~verd
nntext=['красный контур (Пл: ',num2str(polyarea(p(1,:),p(2,:))),...
',Пер.: ' num2str(per(p)) ') не вложен в зелёный (Пл: ',...
num2str(polyarea(ps(1,:),ps(2,:))),',Пер.: ',num2str(per(ps)) ')'];
set(findobj('style','text'),'string',nntext);
end
set(mainaxes,'ButtonDownFcn',[]);
set(get(mainaxes,'parent'),'WindowKeyPressFcn',[]);
end
%centpoint=mean(mincon{mini}(:,1:end-1),2);
%contarea=polyarea(mincon{mini}(1,1:end-1),mincon{mini}(2,1:end-1));
% text(centpoint(1),centpoint(2),num2str(contarea),...
% 'LineWidth',2,'color','white','FontSize',14,...
% 'parent',mainaxes);
end
% -------------------------------------------------------------------
function uipt_manual_ClickedCallback(hObject, eventdata, handles)
global i p n imag;
if isempty(imag)
errordlg('You must select picture!');
return
end
i=1;
n=0;
p=[];
firsttext='Выделите первый контур (ставить точки нажатием левой клавиши мыши) по часовой стрелке. когда закончите нажмите пробел';
set(handles.maintext,'String',firsttext);
set(handles.mainaxes,'buttonDownFcn',@clickfcn);%,'nextplot','add');,'xlimmode','manual','ylimmode','manual');
set(findobj(handles.mainaxes,'type','image'),'hitTest','off');
set(handles.figure1,'WindowKeyPressFcn',@keypressfcn);
end
function clickfcn(ar1,ar2)
global i n p;
r=get(ar1,'currentPoint');
r=r(1,1:2);
if n==0
col='g';
else
col='r';
end
plot(gca,r(1),r(2),[col '*']);%text(r(1),r(2),num2str(i));
i=i+1;
p=[p,r'];
if size(p,2)>1
line(p(1,i-2:i-1),p(2,i-2:i-1),'color',col,'linewidth',1.5);
end
end
function keypressfcn(ar1,ar2)
if ~strcmp(ar2.Key,'space')
return
end
global i p n ps;
per=@(p)sum(sqrt(sum(([p(:,2:end) p(:,1)]-p).^2,1)));
ntext='выделите внутренний контур, и нажмите пробел';
set(findobj(ar1,'type','uicontrol'),'string',ntext);
if size(p,2)<3
ntext='выделите контур';
set(findobj(ar1,'type','uicontrol'),'string',ntext);
return
end
if n==0
col='g';
else
col='r';
end
line(p(1,[size(p,2) 1]),p(2,[size(p,2) 1]),'color',col,'linewidth',1.5);
if n==0
ps=p;
i=1;
p=[];
n=1;
else
poly=discrip(ps);
verd=true;
for j=1:size(p,2)
if ~poly(p(:,j))
verd=false;
break
end
nntext=['красный контур (Пл: ',num2str(polyarea(p(1,:),p(2,:))),...
',Пер.: ' num2str(per(p)) ') вложен в зелёный (Пл: ',...
num2str(polyarea(ps(1,:),ps(2,:))),',Пер.: ',num2str(per(ps)) ')'];
set(findobj(ar1,'type','uicontrol'),'string',nntext);
end
if ~verd
nntext=['красный контур (Пл: ',num2str(polyarea(p(1,:),p(2,:))),...
',Пер.: ' num2str(per(p)) ') не вложен в зелёный (Пл: ',...
num2str(polyarea(ps(1,:),ps(2,:))),',Пер.: ',num2str(per(ps)) ')'];
set(findobj(ar1,'type','uicontrol'),'string',nntext);
end
set(handles.mainaxes,'buttonDownFcn',[]);
set(handles.figure1,'WindowKeyPressFcn',[]);
end
end
function poly=discrip(ps)
i=1;
while i<size(ps,2)
if all(ps(:,i)==ps(:,i+1))
ps=[ps(:,1:i) ps(:,i+2:end)];
continue
end
i=i+1;
end
result=concave2convex(ps);
fun=[];
for i=1:length(result)
rs=['result{' num2str(i) '}'];
fun=[fun '(all(' rs '.A*x<=' rs '.C))|'];
end
fullexp=['poly=@(x)' fun(1:end-1) ';'];
eval(fullexp);
end
[1] В сущности, перемещение точек (пятен) спеклограмы можно интерпретировать как перестановку элементов множества точек, то есть изоморфизм множества точек, отображающий модель на себя или, иными словами, его автоморфизм. Аналогичное существенно для соответствующих ему групп. Автоморфизмом групп в данном случае является изоморфизм группы на себя – совокупность автоморфизмов некоторой модели спеклов с операцией композиции и тождественным отображением. Композиция в данном случае следует в биективной форме, так как композиция инъекции и сюръекции на выходе дает биекцию, а тождественность отображения вытекает из условий эксперимента.
[2] Авторами тестировались варианты с использованием шаговых двигателей с числовым программным управлением и с использованием робота-манипулятора, управляемого по универсальной серийной шине USB. Использование последнего представляется более оправданным в силу большего количества степеней свободы перемещения лазерного источника.
[3] Метод ER-диаграмм (ERD, от англ. entity-relationship diagram – диаграммы сущность-связь) – графический способ нотации моделей данных с помощью блоков и векторов связи, описывающих объекты и отношения между ними. Приближенно по смыслу к российскому понятию блок-схема.
[4] Так называемая топологическая интерференция: см., напр., "Topological interference: singular optics, optical vortices and polarization singularities" (www.dops.dk/downloads/mrdabstract.doc).
[5] Изображения окна программы даны для Windows XP Professional и Windows 7 соответственно для показа возможностей совместимости графического интерфейса. Совместимость проверялась на одном компьютере с установленной виртуальной машиной VMware® Workstation.
[6] Упрощенно подобный массово-символьный подход без экспериментальной реализации показан в брошюре A.Г. Угoдчикoвa "Основы теоретической биологии (клеточный уровень)", М., 2002, 56 с.
[7] В действительности не рекомендуется, но возможна конструктивная минимизация установки путем отказа от манипулятора, пятиосного ротационного столика, измерительной системы контроля и протоколирования перемещения лазерного источника, зеркальной цифровой камеры (замены её на более простую), комплекта лазерных диодов и модулей (сведение к одному наиболее дешевому и популярному красному источнику).