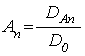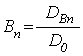УДК 537.874; 537.624

ДВА ПРОСТЫХ АЛГОРИТМА ОПРЕДЕЛЕНИЯ АМПЛИТУД ВНЕШНИХ И ВНУТРЕННИХ КОЛЕБАНИЙ ПРИ РАСПРОСТРАНЕНИИ ВСТРЕЧНЫХ ВОЛН В МНОГОСЛОЙНОЙ НЕОДНОРОДНОЙ СТРУКТУРЕ

 

И. В.Антонец ¹, Л. Н.Котов ¹, В. Г.Шавров ², В. И.Щеглов ²

¹ Сыктывкарский государственный университет, Сыктывкар, Россия

² Институт радиотехники и электроники РАН, Москва, Россия

Получена 15 января 2013 г.

 

Аннотация. Предложены два простых алгоритма получения аналитических выражений для амплитуд выходящих и внутренних волн в многослойной ступенчато-неоднородной структуре при падении двух встречных волн. Работа алгоритмов продемонстрирована на примерах аналитических выражений для амплитуд волн в структуре из трех-пяти слоев, а также численного решения задачи о распространении волн в структуре из 16 слоев с линейным изменением волнового числа по длине. Показана возможность обобщения полученных результатов на случай электромагнитных волн для нормального и наклонного падения.

Ключевые слова: распространение волн, многослойные неоднородные структуры.

Abstract. Two simple algorithms are proposed for deriving analytical expressions for the amplitudes of outgoing and inner waves in multilayer stepwise inhomogeneous structure by the incidence of two counterpropagating waves. The work of these algorithms is demonstrated on the analytical solution for three, four and five layer structure and numerical solve of waves propagation in structure with linear changing of  along its length. It is shown that these algorithms can applied to problems on propagation of electromagnetic waves in the cases of the normal and oblique incidence.

Keywords: wave propagation, multilayer nonuniform structure.

 

Введение

    Задачи о волнах различной природы в слоистых и неоднородных средах издавна привлекают внимание исследователей [1-9]. Для таких задач наиболее последовательным является прямой метод, заключающийся в решении волновых уравнений в каждом слое по отдельности с последующим сшиванием полученных решений на границах [2-5]. При постоянных параметрах слоев метод приводит к системе линейных уравнений, количество которых равно удвоенному числу границ раздела. При большом числе слоев решение такой системы требует раскрытия громоздких определителей высоких порядков [10-15]. Объем вычислений заметно сокращается при применении методов последовательных вычислений – характеристической матрицы [3] и поверхностного импеданса [1]. Однако при любом из упомянутых методов для общего количества слоев более трех вычисления становятся весьма громоздкими.

    В случае неоднородных сред положение усложняется отсутствием универсальных способов решения волновых уравнений с зависящими от координат коэффициентами. Некоторые решения частных видов рассмотрены в работах [2,8,16]. Стандартным приемом здесь является приближение плавной неоднородности среды ступенчатой функцией [2]. В этом случае требование достаточной точности вынуждает разбивать структуру на весьма большое число ступенек, в результате чего аналитический расчет становится невозможным, а численный – довольно громоздким.

    Важнейшим вопросом для многослойных структур является изучение распространения встречных волн, при котором формируется интерференционный поток, обеспечивающий перенос энергии в обоих направлениях [17-22]. Однако вследствие громоздкости вычислений в перечисленных работах рассмотрение ограничено лишь однослойными однородными структурами.

    Заметное облегчение как аналитических, так и численных расчетов дает предложенный в работе [23] алгоритм определения амплитуд отраженной и проходящей волн, состоящий в последовательных вычислениях на основе симметрии прямого метода. В работах [24, 25] предложен более совершенный алгоритм, позволяющий определять амплитуды волн во всех внутренних слоях структуры по отдельности. Работа обоих алгоритмов продемонстрирована на некоторых примерах, однако вопрос о распространении встречных волн рассмотрен неполно.

    Настоящая работа посвящена дальнейшему развитию упомянутых алгоритмов расчета амплитуд колебаний в отдельных слоях структуры, в первую очередь, применительно к задаче о распространении встречных волн. Основное рассмотрение проведено для одномерной волны, после чего показано, как полученные результаты могут быть обобщены на электромагнитные волны.

 

1. Геометрия задачи и решение прямым методом

    Геометрия задачи аналогична принятой в работах [23-25]. Рассматривается падение двух встречных одномерных волн на многослойную неоднородную структуру, показанную на рис.1.

 

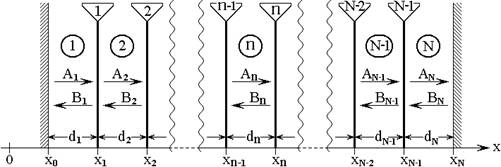
Рис.1. Геометрия задачи.

 

    Структура состоит из  слоев, разделенных  границами. Амплитуды волн, распространяющихся в положительном направлении оси , обозначены буквами , в отрицательном – , волновые числа – , где  - номер слоя. Амплитуды падающих на структуру встречных волн  и  заданы: , , где  - фаза волны  относительно волны . При  и  отражение отсутствует.

    Применение прямого метода к данной задаче дает совокупность решений в слоях 1, … , N вида: 

,                                           (1)

подстановка которых в граничные условия равенства волновых функций и их производных приводит к системе  линейных алгебраических уравнений для амплитуд , … , , , … , , выраженных через амплитуды  и . Решение этой системы методом расширенной матрицы дает детерминанты: , , , … , , , определяющие амплитуды волн:

;  .                                                                                 (2)

 

Для удобства записи далее введены обозначения:

  и .                                                       (3)

    Решение полной задачи нахождения амплитуд волн  и  через  и  при заданных волновых числах , сводится к нахождению детерминантов , , , … , , .

    Рассмотрим сначала алгоритм получения детерминантов, соответствующих амплитудам волн, выходящих из структуры в обоих направлениях. Будем называть это алгоритм «укороченным» и приведем его аналитическую структуру и вариант численной реализации, следуя работе [23].

 

2. Реализация укороченного алгоритма

Введем обозначения:

;                                                                                                      (4)

;                                                                                                     (5)

;                                                                                                     (6)

;                                                                                                     (7)

.                                                                                                       (8)

С использованием (4)-(8) формируем выражения:

;                                                                    (9)

;                                                                    (10)

;                                                                    (11)

;                                                                    (12)

.                                                                                                     (13)

Увеличивая номера индексов на единицу, получаем следующую группу подобных выражений и так далее. Формулы для получения последующих выражений из предыдущих при произвольном номере  имеют вид:

;                                                             (14)

;                                                            (15)

;                                                            (16)

;                                                            (17)

.                                                                                           (18)

Процесс заканчивается при достижении  значения . При этом искомые детерминанты равны:

;                                                                                                        (19)

;                                                                            (20)

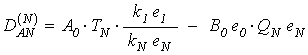.                                                           (21)

 

Из этих выражений получаем амплитуды внешних волн:

;     .                                                   (22)

Численная реализация укороченного алгоритма осуществляется аналогично [23] с помощью программы, блок схема которой показана на рис.2. Как видим, программа содержит всего один цикл, повторяемый  раз. 

 

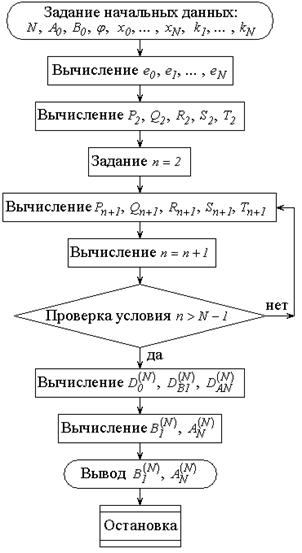
Рис.2. Блок схема укороченного алгоритма вычисления амплитуд внешних волн.

 

3. Применение укороченного алгоритма для вычисления амплитуд внешних волн

    Применим теперь описанный алгоритм к решению задачи о падении двух встречных волн на многослойную ступенчато-неоднородную структуру.

    Пусть структура имеет полную длину  и содержит 16 слоев одинаковой толщины . Каждый слой является однородным, границы между слоями – резкие, то есть волновое число в структуре меняется ступенчатым образом: в пределах каждого слоя остается постоянным, а на границах между слоями скачкообразно меняется.  

    Рассмотрим два случая.

1) волновое число по координате линейно возрастает: 

;                                                                                      (23)

2) волновое число по координате линейно убывает:

;                                                                                   (24)

где  – номер слоя, координата  измерена в , волновое число  –  в .

    Зависимость волнового числа от координаты для этих двух случаев показана на рис.3. Кривая 1 отражает возрастание волнового числа в соответствии с формулой (23), кривая 2 – убывание в соответствии с формулой (24).

 

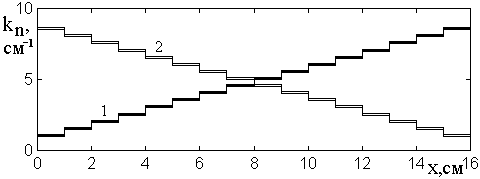
Рис.3. Зависимость волнового числа от координаты.

 

    На структуру падают две встречных волны. Со стороны среды 1 падает волна прямого направления с амплитудой . Со стороны среды 16 падает волна обратного направления с амплитудой  . В среде 1 распространяется волна обратного направления с амплитудой . В среде 16 распространяется волна прямого направления с амплитудой . Все амплитуды нормируются на , поэтому для простоты будем считать .

    Положим амплитуду   постоянной и будем менять амплитуду падающей волны обратного направления . Что происходит при этом с амплитудами волн  и , выходящих из структуры в обоих направлениях, показано на рис.4, где приведены зависимости этих амплитуд от амплитуды . Кривые 1 и 2 (сплошные линии) соответствуют возрастанию волнового числа (23), кривые 3 и 4 (пунктирные линии) – его убыванию (24). Кривые 1 и 3 соответствуют амплитуде , кривые 2 и 4 – амплитуде . Амплитуда падающей волны  меняется от  до , причем знак плюс соответствует синфазности волн  и , знак минус – их противофазности.

 

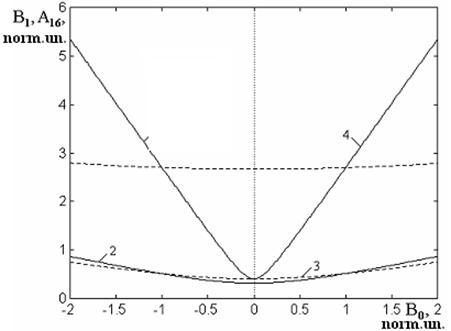
Рис.4. Зависимости амплитуд выходящих из структуры волн обоих направлений от амплитуды падающей волны обратного направления.

 

    Из рисунка видно, что в обоих случаях изменения волнового числа зависимости амплитуд выходящих волн от амплитуды волны обратного направления имеют V-образный характер с минимумом вблизи  , а при увеличении  с тем или иным знаком возрастают по закону, близкому к линейному. Минимум кривой 1 приходится на , минимум кривой 2 – на . Минимумы кривых 3 и 4 приходятся на  и  соответственно.

    Таким образом, приведенные на рис.4 кривые не являются относительно вертикальной оси полностью симметричными. Для выявления степени их несимметричности в следующей таблице приведены численные значения амплитуд выходящих из структуры волн в обратном  и прямом   направлениях, при различных значениях амплитуды падающей волны встречного направления . Верхний индекс «» соответствует нарастанию плотности среды по мере увеличения координаты , индекс «–» – соответствует убыванию плотности среды по мере увеличения . Законы нарастания и убывания плотности среды определяются формулами (23) и (24). Нижний индекс соответствует номеру слоя. Как и ранее, все амплитуды нормированы на , где .

 

 

    Из таблицы видно, что изменение фазы падающей волны встречного направления на противоположную (то есть переход от  к ) меняет амплитуды выходящих волн на величину порядка  , что количественно отражает хотя и невысокую, но ненулевую степень несимметричности кривых, приведенных на рис.4.     

    Можно полагать, что наличие минимумов и близкий к линейному рост амплитуд  и  при достаточном увеличении абсолютной величины  обусловлены стремлением к пропорциональности амплитуд обеих выходящих волн амплитуде той падающей волны, амплитуда которой значительно превышает амплитуду другой. Некоторые сдвиги минимумов кривых по горизонтальной оси  относительно друг друга, по-видимому, обусловлены фазовыми соотношениями между потоками энергии волн прямого и обратного направлений.

 

4. Реализация полного алгоритма

    Рассмотрим теперь алгоритм получения детерминантов, соответствующих амплитудам всех, как внешних, так и внутренних волн, распространяющихся в структуре в обоих направлениях. Будем называть это алгоритм «полным», его краткая реализация приведена в работах [24, 25]. Дадим здесь наиболее удобный вариант, не содержащий громоздких многократных произведений.

            ЭТАП №1.

Введем обозначение:

,                                                                                                                (25)

и положим начальную тройку основных обозначений:

;                                                                                                                (26)

;                                                                                                                (27)

.                                                                                                    (28)

С использованием (26)-(28) формируем новую тройку выражений:

;                                                                      (29)

;                                                                    (30)

.                                                                                                   (31)

Увеличивая порядковые номера индексов на единицу, получаем следующую тройку подобных выражений и так далее, вплоть до , , . Общие формулы при произвольном  имеют вид:

;                                                            (32)

;                                                        (33)

.                                                                                           (34)

Процесс заканчивается при достижении  значения . При этом получаем:

;                                         (35)

;                                         (36)

.                                                                                           (37)

 

            ЭТАП №2.

Введем обозначение:

,                                                                                                           (38)

и положим другую начальную тройку обозначений: 

;                                                                                                               (39)

;                                                                                                               (40)

.                                                                                         (41)

С использованием (39)-(41) формируем тройку выражений:

,                                                      (42)

,                                                 (43)

.                                                                                  (44)

Далее, уменьшая порядковые номера индексов на единицу, получаем следующую тройку подобных выражений и так далее, вплоть до , , . Общие формулы для получения последующих выражений из предыдущих при произвольном номере    имеют вид:

,                                                           (45)

,                                                        (46)

.                                                                                      (47)

Процесс заканчивается при достижении   значения :

,                                                                     (48)

,                                                                   (49)

.                                                                                                 (50)

 

После прохождения обоих этапов, находим детерминанты:

;                                                                                                     (51)

;                                                                (52)

;                                                              (53)

;                                                               (54)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

;                                                        (55)

;                                                         (56)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

;                                                  (57)

.                                                                                                     (58)

 

Здесь индексы детерминантов соответствуют номерам слоев, а выражения (51) и (58) равны друг другу.

    Найденные детерминанты (51)-(58) позволяют определить амплитуды всех внутренних волн структуры через   и  с помощью формул вида (2), задающих амплитуды волн в точках их исхода. При этом амплитуды внешних волн равны:

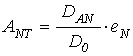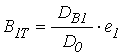,         .                                                             (59)

 

    Непосредственной проверкой можно убедиться, что эти амплитуды совпадают с выражениями (22), полученными с помощью укороченного алгоритма.

    В рамках приведенного здесь алгоритма прибавление одного дополнительного слоя увеличивает объем записи всего в два раза, причем происходит простое автоматическое дублирование предыдущей записи с увеличением номеров индексов на единицу, что технически весьма просто.    

    Полный алгоритм, также как и укороченный, легко реализуется в численном виде. Возможная блок-схема программы приведена на рис.5.

 

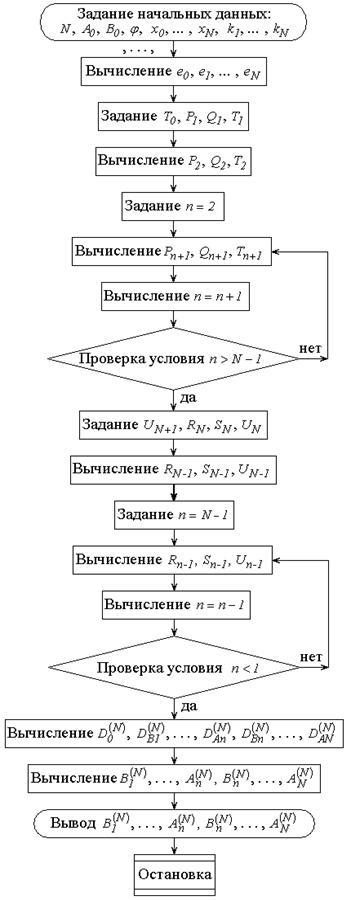
Рис.5. Блок схема полного алгоритма вычисления амплитуд волн.

 

    Можно видеть, что программа содержит всего два цикла, повторяемые   раз. Таким образом, предложенный полный алгоритм позволяет получать как аналитические выражения, так и численные значения для детерминантов весьма высоких порядков при минимальных вычислительных затратах.

 

5. Детерминанты для трех, четырех и пяти слоев

    Приведем теперь полученные с помощью обоих алгоритмов аналитические выражения детерминантов для трех, четырех и пяти слоев.

    Так, для случая трехслойной структуры  , где решение прямым методом требует раскрытия пяти определителей четвертого порядка, получаемые здесь детерминанты имеют вид: 

;                                                   (60)

;                 (61)

;                                                  (62)

;                                                 (63)

.                (64)

Амплитуды волн , , ,  имеют вид:

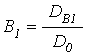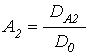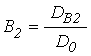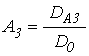;   ;   ;   .                                     (65)

 

    Легко убедиться, что эти выражения совпадают с полученными прямым методом [10,11], однако объем вычислений здесь резко уменьшается.

    Для структуры из четырех слоев  , требующей раскрытия семи определителей шестого порядка, детерминанты имеют вид: 

   ;                                (66)

 

                            ;                                                  (67)

 

 

                          ;                                            (68) 

 

 

                           ;                                               (69) 

 

 

  ;                       (70)

 

 

  ;                           (71)

 

 

       .                     (72)

 

   ;                                 (73)

 

Амплитуды волн , , , , ,  имеют вид:

;          ;          ;

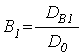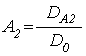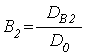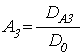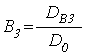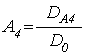        ;          ;          .                                       (74)

 

    Наконец, для случая пяти слоев  , где при прямом методе требуется раскрытие девяти определителей восьмого порядка, получаемые с помощью алгоритма детерминанты имеют вид: 

;                              (75)

 

                         ;                                            (76)

 

                         ;                                      (77)

 

                         ;                                        (78)

 

 

;                  (79)

 

 ;                    (80)

 

  ;                  (81)

 

  ;                      (82)

 

;       (83)

 

;             (84)

 

Амплитуды волн , , , , , , ,  имеют вид:

;     ;      ;      ;         

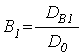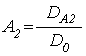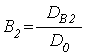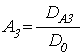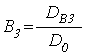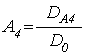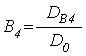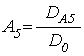;      ;      ;      .                               (85)

 

    Для числа слоев большего пяти решение прямым методом становится крайне громоздким, а для   слоев требует раскрытия   определителей порядка

  , причем объем вычислений растет как факториал от . То есть применение описанных алгоритмов при числе слоев более пяти становится весьма целесообразным.

 

6. Применение полного алгоритма для вычисления амплитуд внутренних и внешних волн

    Применим теперь описанный алгоритм к решению задачи о падении двух встречных волн на многослойную ступенчато-неоднородную структуру. Для удобства сравнения рассмотрим ту же структуру, что и для укороченного алгоритма.

    Будем рассматривать те же два случая:

1) волновое число линейно возрастает в соответствии с формулой (23);

2) волновое число линейно убывает в соответствии с формулой (24).

    Как и ранее, зависимость волнового числа от координаты для этих двух случаев показана на рис.1.

    На структуру падают две встречных волны: со стороны среды 1 с амплитудой  и со стороны среды 16 с амплитудой . Внутри слоев структуры распространяются внутренние волны обоих направлений с амплитудами   и   в соответствии с рис.1, а также внешние: в среде 1 – волна обратного направления с амплитудой , в среде 16 – волна прямого направления с амплитудой . Все амплитуды нормируются на , где .

    На рис.6 показано распределение амплитуд волн в различных слоях структуры в случае возрастания волнового числа по координате (23) для волн прямого (а) и обратного (б) направлений. Кривые 1 – 4 соответствуют различным значениям амплитуды встречной волны  от   до  с шагом .

 

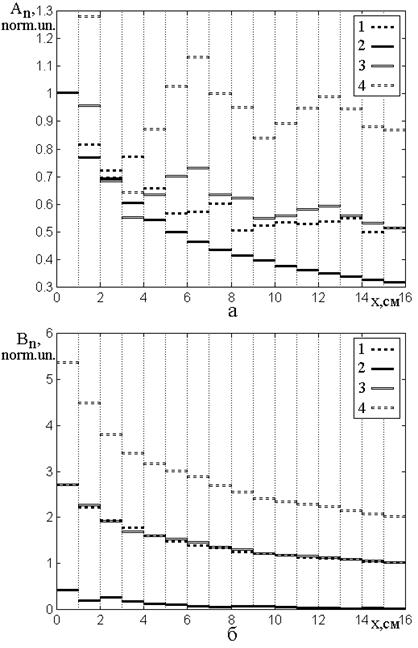
Рис.6. Распределение амплитуд волн в различных слоях структуры для случая возрастания волнового числа по координате. а – амплитуды волн прямого направления, б – амплитуды волн обратного направления.

1 – ; 2 –; 3 – ; 4 – ;

 

    Из рисунка видно, что амплитуды внешних волн  и  при заданных значениях  соответствуют амплитудам тех же волн, приведенным на рис.4.

    Из рис.6а видно, что амплитуды волн прямого направления монотонно спадают с координатой только в случае  (кривая 2), то есть в отсутствие встречной волны, а во всех остальных случаях носят осциллирующий характер, что говорит о наличии интерференционных явлений. Амплитуды волн прямого направления при  и  (кривые 1 и 3), совпадая в крайних слоях структуры, во внутренних ее слоях сильно различаются между собой. Такое обстоятельство говорит о высокой критичности амплитуд внутренних волн к соотношению фаз волн, падающих с прямого и обратного направлений.

    Из рис.6б видно, что амплитуды волн обратного направления с увеличением значения координаты всегда плавно спадают подобно друг другу, причем кривые для  и  (1 и 3) практически совпадают между собой, что говорит о незначительности роли интерференции в распространении этих волн. Увеличение амплитуд кривых при увеличении абсолютной величины  отражают рост амплитуды падающей волны встречного направления. 

 

    На рис.7 показано распределение амплитуд волн в различных слоях структуры в случае убывания волнового числа по координате (24) для волн прямого (а) и обратного (б) направлений. Кривые 1 – 4 соответствуют различным значениям амплитуды встречной волны  от  до  с шагом .

    Из этого рисунка также видно, что амплитуды внешних волн  и  при заданных значениях  соответствуют амплитудам тех же волн, приведенным на рис.4.

    Из рис.7а видно, что все амплитуды волн прямого направления (1-4) монотонно нарастают приблизительно одинаково (различие не превышает ) при всех значениях амплитуды падающей волны обратного направления . Нарастание связано с распространением волны из более плотной среды в менее плотную и обусловлено сохранением энергии. Близость кривых 1-4 друг к другу свидетельствует в пользу отсутствия интерференционных явлений и коррелирует с подобным спадом аналогичных кривых для волн противоположного направления, приведенных на рис.6б (в обоих случаях волна распространяется в сторону уменьшения плотности среды). Совпадение приведенных здесь кривых 1-4 друг с другом по сравнению с разбросом кривых 1-4 на рис.6б обусловлено неизменностью амплитуды падающей волны: здесь для всех кривых , там для кривых 1-4 амплитуда  меняется от  до .

 

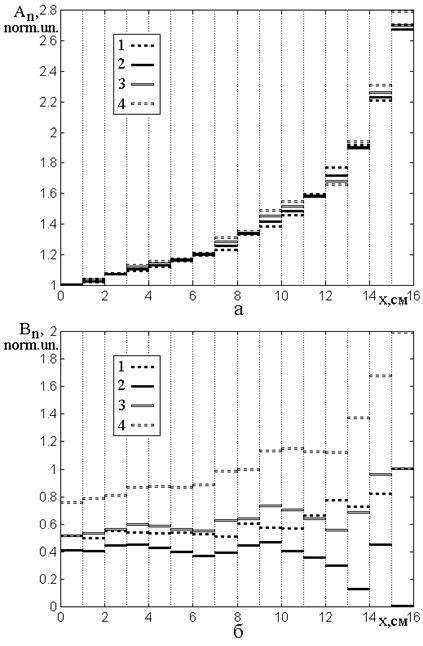
Рис.7. Распределение амплитуд волн в различных слоях структуры для случая убывания волнового числа по координате. а – амплитуды волн прямого направления, б – амплитуды волн обратного направления.

1 – ; 2 –; 3 – ; 4 – ;

    Из рис.7б видно, что амплитуды волн обратного направления при изменении координаты во всех случаях заметно осциллируют, что говорит о высокой роли интерференции в их формировании. Амплитуды волн обратного направления при  и  (кривые 1 и 3), совпадая в крайних слоях структуры, во внутренних ее слоях заметно (до ) различаются между собой, что свидетельствует в пользу высокой критичности амплитуд внутренних волн к соотношению фаз волн, падающих с прямого и обратного направлений. Размах осцилляций амплитуд волн обратного направления при убывании волнового числа (рис.7б) также коррелирует с размахом амплитуд волн прямого направления при нарастании волнового числа (рис.6а). Таким образом, можно видеть, что степени размаха кривых для волн прямого и обратного направлений при изменении знака изменения волнового числа как бы меняются местами. То есть, кривые, соответствующие волнам, направление распространения  которых совпадает с направлением увеличения плотности среды, испытывают значительно более сильный размах, чем волны противоположного направления, что говорит о значительно более сильной роли интерференционных явлений в этом случае.

 

7. Обобщение на случай электромагнитных волн

    Предложенные алгоритмы и получаемые с их помощью детерминанты легко обобщить на случай электромагнитных волн, например как это сделано в работах [10,11,15]. Так, для случая нормального падения достаточно во всех выражениях, кроме показателей экспонент, заменить волновые числа величинами, обратными соответствующим импедансам:

,                                                                                                       (86)

где: ,   - импеданс пустого пространства, а  и   – магнитная и диэлектрическая проницаемости -го слоя.

    В случае наклонного падения сначала надо найти углы падения волн обоих направлений во всех слоях структуры. Эти углы в крайних слоях структуры считаются заданными:  и . Остальные углы  между направлением распространения волны в слое  и осью  определяются законом Снеллиуса. Для волн, распространяющихся в положительном направлении оси , начиная с  и , увеличивая индекс на единицу,  последовательно получаем:

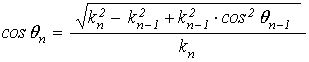.                                                          (87)

 

Для волн, распространяющихся в отрицательном направлении оси , начиная с  и , уменьшая индекс на единицу, последовательно получаем:

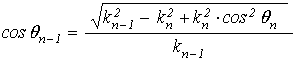.                                                             (88)

 

После того, как все углы  найдены, в случае волн с продольной поляризацией для волновых чисел надо произвести замену:

,                                                                                              (89)

при этом экспоненты преобразуются как:

,                                       (90)

а амплитуды определяются выражениями:

;     .                                                                  (91)

Для волн с поперечной поляризацией замена волновых чисел имеет вид:

,                                                                                               (92)

экспоненты преобразуются в соответствии с формулой (90), а амплитуды  и  остаются без изменений.

 

Выводы

    Предложены два варианта (укороченный и полный) простого алгоритма получения аналитических выражений для амплитуд выходящих (отраженной и проходящей), а также всех внутренних волн в отдельных слоях многослойной структуры со ступенчатой неоднородностью. Рассмотрен случай падения двух встречных одномерных волн при произвольном числе слоев. Получены аналитические выражения амплитуд волн для структур, состоящих из трех, четырех и пяти слоев.

    Показана возможность численного решения задачи для произвольного числа  слоев, представлены блок-схемы программ для ЭВМ, реализующих оба варианта предложенных алгоритмов на основе одного или двух вычислительных циклов, повторяемых  раз.

    Работа обоих алгоритмов продемонстрирована на примере численного решения задачи о распространении волн в ступенчато-неоднородной структуре с линейным увеличением или уменьшением волнового числа по ее длине.

    С помощью укороченного алгоритма показано, что при постоянной амплитуде падающей волны прямого направления  зависимости амплитуд выходящих из структуры волн обоих направлений  и от амплитуды падающей волны обратного направления , в обоих случаях изменения волнового числа, имеют V-образный характер с минимумом вблизи , а при увеличении  с тем или иным знаком возрастают по закону, близкому к линейному. Отмечена небольшая асимметричность таких зависимостей, обусловленная интерференцией распространяющихся волн.

    Показана возможность численного определения амплитуд внутренних волн в отдельных слоях той же структуры с помощью использования полного алгоритма. При неизменной амплитуде падающей волны прямого направления  исследованы зависимости амплитуд внутренних волн  и  при произвольном значении  от амплитуды падающей волны обратного направления . Показано, что при увеличении волнового числа по координате амплитуды волн прямого направления в отсутствие встречной волны (при ) монотонно спадают по координате, а при  носят осциллирующий характер. Амплитуды волн обратного направления при этом монотонно спадают. При уменьшении волнового числа по координате амплитуды волн прямого направления монотонно нарастают, а амплитуды волн обратного направления имеют осциллирующий характер.

    Показано, что координатные зависимости амплитуд, соответствующих волнам, направление распространения  которых совпадает с направлением увеличения плотности среды (увеличения волнового числа), испытывают значительно более сильные осцилляции, чем волны противоположного направления. Наблюдаемый ход кривых интерпретирован на основе интерференционных явлений в сочетании с сохранением энергии распространяющейся волны.

    Показана возможность обобщения полученных результатов на случай электромагнитных волн при нормальном и наклонном падении с продольной и поперечной поляризациями.  

 

    Работа поддержана РФФИ (гранты №10-02-01327-а, №12-02-01035-а).

 

Литература

    1. Бреховских Л.М. Волны в слоистых средах. М.: Наука. 1973.

    2. Бреховских Л.М., Годин О.А. Акустика слоистых сред. М.: Наука. 1989.

    3. Борн М., Вольф Э. Основы оптики. М.: Наука. 1970.

    4. Розенберг Г.В. Оптика тонкослойных покрытий. М.: Гос.изд.физ-мат.лит. 1958.

    5. Кизель В.А. Отражение света. М.: Наука. 1973.

    6. Oksanen M.I., Hanninen J., Tretyakov S.A. // IEEE Proc. H. 1991. V.138. №7. P.513.

    7. Sarychev A.K., Bergman D.J., Yagil Y. // PR(B). 1995. V.51. №8. P.5366.

    8. Шварцбург А.Б. // УФН. 2000. Т.170. №12. С.1297.

    9. Шалин А.С., Моисеев С.Г. // Оптика и спектроскопия. 2009. Т.106. №6. С.1004.

    10. Антонец И.В., Щеглов В.И. Распространение волн через тонкие слои и пленки. Сыктывкар: ИПО СыктГУ. 2010.

    11. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры. Часть первая. Прямой метод. Сыктывкар: ИПО СыктГУ. 2011. 

    12. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2007. Т.52. №4. С.403.

    13. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2008. Т.53. №4. С.389.

    14. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ.  2009. Т.54. №10. С.1171.

    15. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2010. Т.55. №2. С.133.

    16. Рэлей Дж.У. Теория звука. Т.1,2. М.: ИЛ. 1955.

    17. Колоколов А.А., Скроцкий Г.В. // УФН. 1992. Т.162. №12. С.165.

    18. Сидоренков В.В., Толмачев В.В. // Письма в ЖТФ. 1990. Т.16, №3. С.20.  

    19. Кузнецов Ю.Н., Семенцов Д.И. // ЖТФ. 2005. Т.75. №11. С.81.

    20. Ефимов В.В., Семенцов Д.И. // ЖТФ. 1997. Т.67. №2. С.118.

    21. Афанасьев С.А., Семенцов Д.И. // ЖТФ. 1997. Т.67. №10. С.77.

    22. Санников Д.Г., Семенцов Д.И. // ПЖТФ. 2007. Т.33. №23. С.19.

    23. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2011. Т.57. №1. С.67.

    24. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Сборник трудов XIX Международной конференции «Электромагнитное поле и материалы». Москва-Фирсановка: «НИУ МЭИ». 2011. С.154.

    25. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. //  РЭ. 2013. Т.58. №1. С.16.