УДК 535.36, 537.874

ОПТИМИЗАЦИЯ РЕЗОНАНСНЫХ СВОЙСТВ МЕТАЛЛИЧЕСКИХ ФОТОННЫХ КРИСТАЛЛОВ

 

А. Ю. Ветлужский, Г. Ю. Лизунов

Институт физического материаловедения СО РАН

 

Получена 11 декабря 2012 г.

 

Аннотация: Рассматриваются способы оптимизации параметров металлических фотонных кристаллов, позволяющие достичь максимального проявления ими резонансных свойств, заключающихся в локализации электромагнитного излучения внутри кристалла на определенных частотах.

Ключевые слова: фотонные кристаллы, локализация излучения, резонанс, многократное рассеяние.

Abstract: The methods of optimizing the parameters of metallic photonic crystals, allowing to achieve the maximum development of the resonance properties, consisting in the localization of electromagnetic radiation within the crystal at specific frequencies are considered in the article.

Key words: photonic crystals, the localization of the radiation, resonance, multiple scattering.

 

1. Введение

Фотонные кристаллы (ФК) – это структуры или композитные материалы, диэлектрическая проницаемость которых меняется периодически в некоторых направлениях с периодом, сопоставимым с длиной волны излучения [1, 2]. Основным свойством ФК является наличие запрещенных зон, т.е. диапазонов частот, в которых полностью подавляется распространение электромагнитных волн через такие структуры.

         Несмотря на уникальные свойства трехмерных структур, наиболее перспективными для практического применения в ближайшие годы принято считать двумерные ФК, обладающие пространственной периодичностью в двух ортогональных направлениях. Такие структуры просты в реализации, но при этом позволяют создавать весьма эффективные устройства преобразования, каналирования и локализации электромагнитного излучения различных диапазонов [3].

         Примером могут служить ФК с дефектами структуры. Введение дефекта в ФК приводит к появлению дефектных мод в запрещенной зоне, в результате чего возникают новые эффекты во взаимодействии излучения с ФК [4, 5]. Одним из них является локализация поля в области дефекта, в результате чего одиночные дефекты могут выступать, например, в качестве объемных резонаторов, а цепочки дефектов – в качестве волноведущих систем, способных функционировать и в СВЧ, и в оптическом диапазонах.

Говоря о практической реализации структур с локальными, одиночными нарушениями регулярности, следует, однако, отметить, что локализация излучения внутри таких ФК возможна только при условии эффективного возбуждения области дефекта. Поскольку на частотах, соответствующих запрещенной зоне, уровень излучения экспоненциально убывает при прохождении внутрь кристалла, указанный способ создания резонаторных структур с высокой добротностью не применим к ФК больших размеров, либо состоящим из элементов с сильно выраженными рассеивающими свойствами.

Подобных недостатков лишены бездефектные ФК [6]. В этих структурах резонансные эффекты проявляются в виде локализации поля в одной или нескольких областях внутри кристалла на частотах, соответствующих разрешенным зонам в спектре их собственных электромагнитных состояний. Это снимает вышеуказанные ограничения, т.к. на этих частотах излучение свободно проходит через сколь угодно протяженные структуры.

Поскольку причина возникновения резонансных эффектов заключается в переизлучении поля внутри пространственно ограниченных систем рассеивателей, целью настоящей работы является изучение влияния линейных размеров двумерных ФК на степень локализации излучения на резонансных частотах и определение оптимальных параметров таких структур для проявления ими резонансных свойств.  

 

2. Результаты численного моделирования и их обсуждение

Рассмотрим сказанное выше на примере ФК, представляющего собой двумерно-периодическую решетку параллельно расположенных металлических цилиндров. Подобные структуры характеризуются наличием полной запрещенной зоны в области низких частот, а также, в отличие от диэлектрических ФК, обладают монотонной зависимостью поперечника рассеяния цилиндрических элементов от частоты, что позволяет рассматривать резонансные свойства структуры в целом без учета собственных резонансных свойств отдельных элементов [7,8].

Численное моделирование взаимодействия электромагнитного излучения с ФК производилось на основе теории многократного рассеяния. Методика расчета применительно к задачам дифракции волн на системах цилиндрических элементов подробно обсуждалась в [9]. Предполагалось, что структура возбуждается полем линейного источника, находящегося на значительном удалении от ФК, при этом вектор напряженности электрического поля ориентирован параллельно цилиндрам (Е - поляризация). Для анализа зонной структуры рассматриваемого кристалла выполнялся расчет частотной зависимости относительной интенсивности поля – , где I и I₀  – интенсивности поля, прошедшего через структуру и в ее отсутствие соответственно. При этом изучение характеристик поля, прошедшего через ФК, проводилось на основе определения величины , имеющей в данном случае смысл коэффициента прохождения, хотя и определяемого вблизи рассматриваемой структуры.

         На рис. 1 представлены результаты моделирования спектра пропускания регулярного двумерного ФК, представляющего собой квадратную решетку, образованную 81 круговым металлическим цилиндром (9 рядов по 9 элементов в каждом) радиусом a = 0,05 см и периодом расположения  d = 1,25 см.

 

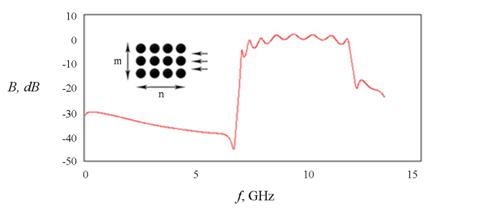
Рис. 1.  Частотная зависимость коэффициента прохождения излучения

 через ФК, состоящий из 81 (n на m) элемента

 

Из рисунка видно, что в определенных диапазонах частот рассматриваемый кристалл не пропускает через себя электромагнитное излучение, практически полностью отражая его в направлении источника, что и позволяет говорить об этих диапазонах как о запрещенных зонах данного ФК.

Рассмотрим подробнее частотный спектр излучения, взаимодействовавшего с описанным выше кристаллом, на примере анализа относительной интенсивности излучения внутри структуры (точка наблюдения поля располагалась вблизи центрального элемента) - рис. 2.

 

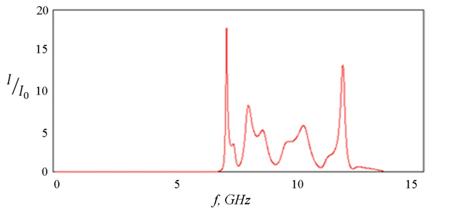
Рис. 2. Частотная зависимость относительной интенсивности поля

в центральной области ФК

 

Из рис. 2 видно, что границы запрещенных зон не поменяли своего положения относительно спектра пропускания, а в пределах разрешенной зоны, расположенной в диапазоне 7,1 – 12,25 ГГц, появились несколько ярко выраженных максимумов, свидетельствующих о локализации поля в центральной области структуры на определенных частотах. Такая локализация, по-видимому, является следствием формирования стоячих волн внутри многоэлементной решетки за счет переотражения излучения ее границами и внутренними рядами элементов, и именно эти эффекты и позволяют говорить о проявлении ФК резонансных свойств.

Наибольшей амплитудой характеризуется первый резонансный максимум, возникающий на частоте перехода от первой запрещенной к разрешенной зоне ФК, причем, как показали дополнительные исследования, это является типичным для любых двумерных регулярных ФК. Поскольку при этом следует ожидать максимальной локализации поля в структуре, все последующие выводы будут касаться оптимизации параметров ФК с целью наилучшего проявления ими резонансных свойств именно на таких частотах. Отметим, что изменение линейных размеров рассматриваемых в работе структур при сохранении периода размещения элементов практически не влияет на частоту первого резонанса ФК.

 

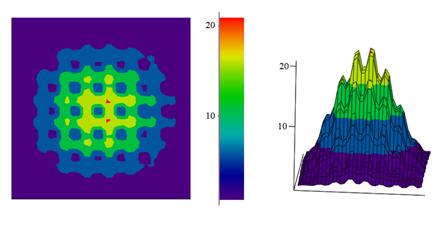
Рис. 3. Пространственное распределение поля в ФК

 на частоте первого резонанса, вид сверху – (а); 3D – (б).

На рис. 3 изображено пространственное распределение поля в ФК на указанной частоте. Действительно, как следует из представленных данных, излучение оказывается локализовано в пределах всего ФК с максимумом в центральной его области. При этом значение относительной интенсивности достигает 20, что, с одной стороны, свидетельствует о существенном перераспределении энергии в ФК, а с другой стороны может оказаться недостаточным для практического применения подобных структур в качестве эффективных резонаторов.     

Представляется достаточно очевидным, что, поскольку локализация излучения возникает из-за внутренних переотражений в структуре, любые изменения рассеивающих свойств систем элементов ФК, либо изменения его геометрии должны приводить к соответствующим изменениям интенсивности поля в области первого резонанса.

Исследуем эту взаимосвязь,  для чего рассмотрим влияние на степень локализации коэффициента заполнения (filling factor) фотонного кристалла, определяемого как отношение площади занимаемой всеми элементами к площади структуры в целом и равного в данном случае . На рис. 4 показана зависимость относительной интенсивности поля в центральной области ФК от его коэффициента заполнения для трех структур, состоящих из различного числа элементов.

 

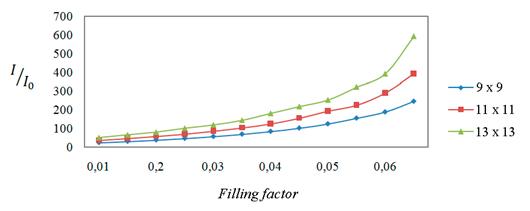
Рис. 4. Зависимость относительной интенсивности поля от коэффициента

 заполнения структуры для разного числа элементов в ФК

 

         Как следует из представленных данных, с увеличением коэффициента заполнения интенсивность поля существенно возрастает. Действительно, с точки зрения оценки межэлементных волновых взаимодействий увеличение поперечных размеров элементов либо уменьшение периода структуры должны проявляться аналогично – через возрастание интенсивности многократного рассеяния волн на ФК, что, в свою очередь, приводит к росту локализации поля в структуре. При этом, однако, влияние геометрических параметров отдельных цилиндров сказывается на величине интенсивности в момент резонанса более существенно, поскольку их изменение приводит как к изменениям межэлементных расстояний, так и к изменению рассеивающих свойств одиночных элементов.  

Анализируя влияние линейных размеров ФК на степень локализации излучения, рассмотрим, как на ней скажется общее увеличение числа элементов в структуре, а также изменение ее протяженности в продольном и поперечном направлениях по отношению к направлению распространения падающей на кристалл волны.

Представленные на рис. 5 результаты расчета иллюстрируют монотонный рост интенсивности излучения в структуре при увеличении количества элементов, ее образующих. При этом оказывается, что уровень интенсивности может достигать достаточно больших значений даже в весьма малоэлементных структурах. 

 

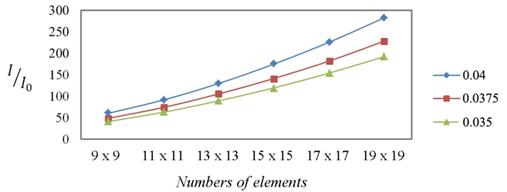
Рис. 5. Зависимость относительной интенсивности поля

от числа элементов в ФК для разных коэффициентов заполнения

 

При увеличении числа элементов в поперечном для падающей на ФК волны направлении интенсивность поля на частоте первого резонанса возрастает (рис. 6). При изменении продольных габаритов ФК аналогичная зависимость имеет немонотонный характер (рис. 7). 

 

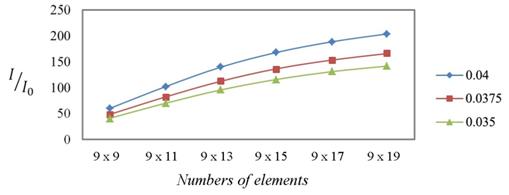
Рис. 6. Зависимость относительной интенсивности поля

от числа элементов в ФК поперек направления облучения

 

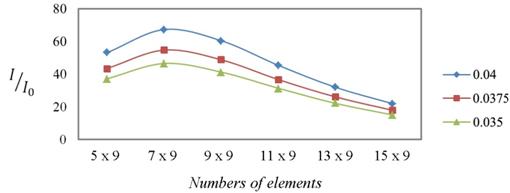
Рис. 7. Зависимость относительной интенсивности поля

от числа элементов в ФК вдоль направления облучения

 

         Последние результаты могут быть интерпретированы следующим образом. Увеличение размеров структуры в поперечном относительно прихода волны направлении приводит к увеличению области «перехвата» падающего на нее излучения, в результате чего растет количество энергии, распределенной по объему структуры, а, следовательно, и интенсивность локализованного излучения в момент резонанса. Однако, основным параметром, определяющим степень проявления структурой резонансных свойств, являются ее продольные размеры. Как следует из рис. 7, для каждого соотношения период ФК – длина волны существует оптимальная линейная протяженность структуры, при которой наблюдается максимальная локализация излучения в центральной области ФК. Если рассматривать ФК как некоторый композитный материал с эффективными значениями диэлектрической проницаемости, то данная длина структуры будет соответствовать половине длины волны излучения в таком материале. При меньших размерах уровень переотражений во внутренних областях структуры оказывается недостаточным для существенной концентрации энергии в центральной области, и она в значительной степени распределяется за пределами ФК, «вытекая» как в прямом, так и в обратном направлениях по отношению к падающему на структуру излучению. Увеличение линейной продольной протяженности ФК сверх некоторой величины для проявления ею резонансных свойств также нежелательно, поскольку при этом нарушаются условия формирования стоячей волны в ФК с единственной пучностью в центральной его области. Так, например, при удвоении длины структуры относительно оптимальной, наблюдаются два максимума в пространственной картине поля в ФК, при этом, поскольку та же энергия распределяется по большей площади, уровень интенсивности в этих областях оказывается значительно ниже, чем в структуре с оптимальной геометрией (рис. 8).

 

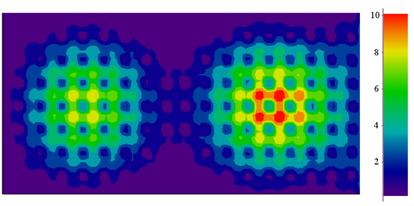
Рис. 8. Пространственное распределение поля в ФК удвоенной,

по сравнению с оптимальной, длины на частоте первого резонанса

 

3. Постановка и результаты экспериментальных исследований

В рамках настоящей работы было выполнено экспериментальное изучение резонансных свойств металлических ФК, ориентированное на верификацию теоретически полученных данных. Эксперименты проводились в СВЧ диапазоне с использованием панорамного измерителя ослаблений и КСВН в волноводных трактах Р2-60, модифицированного для проведения измерений в открытых структурах. Анализировавшийся в экспериментах диапазон частот 5,6 – 8,3 ГГц определялся характеристиками прибора. В качестве излучателя использовался пирамидальный рупор, роль приемной антенны выполнял несимметричный полуволновый вибратор. Система цилиндров, образующих исследуемый резонансный ФК, размещалась перпендикулярно металлической плоскости, при этом высота элементов составляла несколько длин волн, за счет чего исключалось влияние конечности длины цилиндров на результаты измерений.     

Методика измерений заключалась в следующем: при одном и том же пространственном разносе антенн измерялись величины (в дБ) интенсивностей поля в отсутствие структуры В₀ (рис. 9) и при размещении ФК между антеннами В₁. В итоге определялась величина относительной интенсивности поля В = В₁ – В₀ .

 

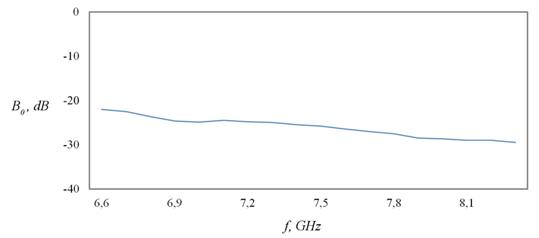
Рис. 9. Калибровочная кривая, описывающая частотную зависимость

поля над гладкой металлической плоскостью
 

При проведении экспериментов в присутствии ФК приемная антенна размещалась, по аналогии с теоретической моделью, во внутренней области ФК на удалении от центрального элемента равном половине периода решетки. При этом диаметр элементов и период их расположения в структуре также соответствовали значениям, выбранным при численных расчетах.

На рис. 10 представлены результаты измерений поля в ФК, представляющем собой решетку 9 на 9 цилиндров. Из рисунка следует, что на частоте 7 ГГц расположен переход от запрещенной к разрешенной зонам в спектре состояний ФК, а на частоте 7,1 ГГц располагается первый резонансный максимум.

 

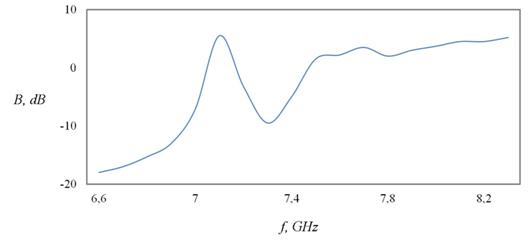
Рис.10. Измеренная относительная интенсивность поля в структуре,

состоящей из 81 (9 на 9) металлического цилиндра

         На рис. 11 изображены результаты численного моделирования спектрального распределения интенсивности поля внутри аналогичного ФК в том же диапазоне частот.

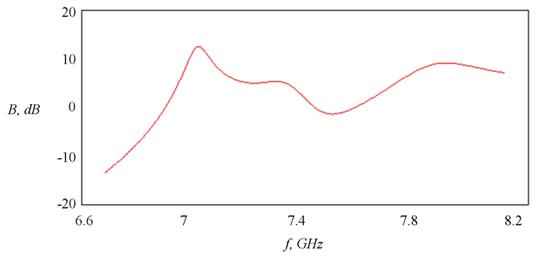
Рис. 11. Рассчитанный относительный уровень интенсивности поля в ФК

 

         Сравнение зависимостей демонстрирует хорошее согласие эксперимента с расчетом. При этом наиболее важным представляются совпадение значений резонансной частоты кристалла в обоих случаях и экспериментальное подтверждение возможности локализации излучения в структуре на данной частоте.

В соответствии с теоретической частью работы было исследовано влияние линейных размеров ФК на эффективность проявления резонансных свойств. При этом все выше сформулированные выводы получили подтверждение. Так, с увеличением количества элементов, образующих ФК, или, иными словами, при одновременном увеличении его протяженности в двух ортогональных направлениях уровень локализованного в структуре излучения на частоте первого резонанса возрастал (рис. 12, 13).

 

        

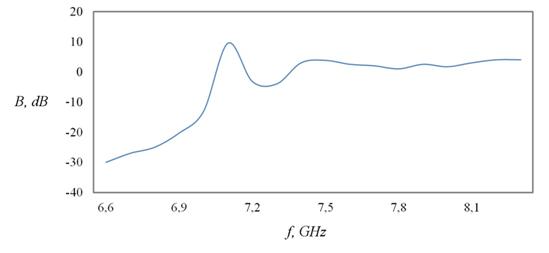
Рис.12. Относительная интенсивность поля в структуре,

состоящей из 81 (11 на 11) металлических цилиндров

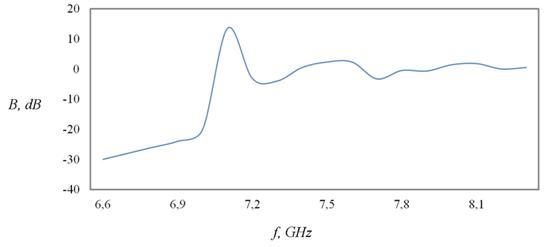
Рис.13. Аналогично рис. 12 для структуры из 169 (13 на 13) элементов

 

         Увеличение протяженности структуры в продольном направлении приводило к понижению величины резонансного максимума (рис. 14, 15), а рост поперечных габаритов ФК – к нарастанию интенсивности поля в момент наступления резонанса (рис. 16, 17). 

 

        

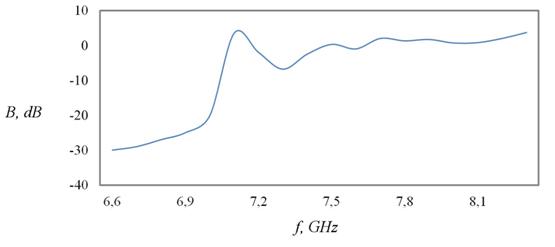
Рис. 14. Аналогично рис. 12 для структуры из 99 (11 на 9) элементов

 

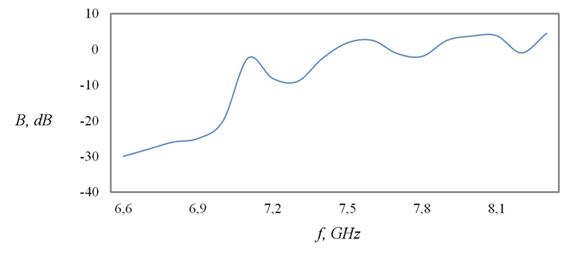
Рис. 15. Аналогично рис. 12 для структуры из 117 (13 на 9) элементов

 

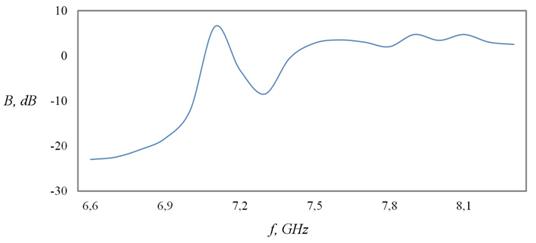
Рис. 16. Аналогично рис. 12 для структуры из 99 (9 на 11) элементов

 

       

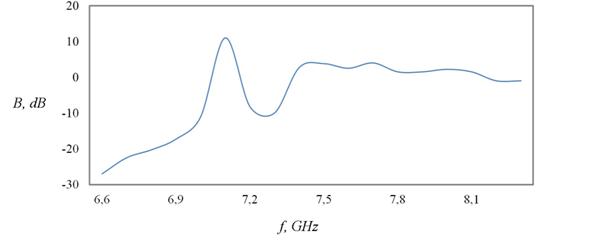
Рис. 17. Аналогично рис. 12 для структуры из 117 (9 на 13) элементов

 

4. Заключение

Таким образом, в работе теоретически и экспериментально исследованы резонансные свойства двумерных металлических ФК. Установлены основные пути усиления локализации излучения внутри ФК кристалла в резонансном режиме за счет изменения плотности компоновки элементов в структуре и оптимизации ее размеров. Показано, что в диапазоне частот, соответствующих разрешенной зоне в спектре собственных состояний кристалла, такая структура может рассматриваться как композитный материал, характеризующийся определенными значениями эффективной диэлектрической проницаемости.  

 

Литература

1. Joannopoulos J., Meade R., Winn J. Photonic Crystals: Molding the Flow of Light. Princeton: Princeton University Press, 1995.

2. Yablonovitch E. // Phys. Rev. Lett. V. 58, № 20. P. 2059-2062.

3. Sakoda K. Optical Properties of Photonic Crystals. Berlin: Springer, 2001.

4. Желтиков А.М., Магницкий С.А., Тарасишин А.В. ЖЭТФ. 2000. Т. 117. № 3. С. 691-701.

5. Zhao Y.-C., Yuan L.-B. // J. Phys. D: Appl. Phys. 2009. V. 42. 015403.

6. Ветлужский А.Ю. // Письма в ЖТФ. 2010. Т. 36. № 13. С 78-85.

7. Sigalas M.M. et al. // Phys. Rev. B. 1995. V. 52. № 16. P. 11744-11751.

8. Лозовик Ю.Е., Эйдерман С.Л. // ФТФ. 2008. Т. 50. № 11. С. 1944-1947.

9. Ветлужский А.Ю. // ЖЭТФ. 2009. Т. 136. № 2. С. 356-361.