Методы сегментации частиц для обработки картин визуализации потоков

А. А. Савин

Национальный исследовательский университет «Московский энергетический институт»

Получена 14 декабря 2012 г., после доработки – 20 декабря 2012 г.

Аннотация. Предложен новый алгоритм сегментации частиц для обработки картин визуализации потоков, основанный на морфологическом анализе изображений. Он заключается в нахождении так называемых линий водораздела, что позволяет различить частицы, изображения которых перекрываются. Методом численного моделирования произведено сравнение предложенного метода с наиболее часто используемым методом, основанном на поиске локальных максимумов на изображении. Показано, что в определенном диапазоне значений отношения сигнал/шум новый метод «находит» большее количество частиц.

Ключевые слова: сегментация частиц, отслеживание частиц, визуализация потоков.

Abstarct.  The new algorithm of particle segmentation for using in flow visualization images, based on morphological analyses of images, is proposed. It based on finding so-called watershed dividing line that allows difference particle,whose images overlap. By numbering modeling two methods, new and typical, based on finding local maximum on image, are compared. It is shown, that at defined range of signal-to-noise ratio values the new method find more particle.

Keywords: particle segmentation, particle tracking, flow visualization.

 

Введение

Одним из распространенных методов измерения полей скоростей потоков жидкости и газа, в том числе, жидкостей в организме человека, в настоящее время является трассерный метод, основанный на цифровой видеозаписи траекторий частиц (трассеров), визуализирующих исследуемый поток, с последующим компьютерным анализом получившихся изображений [1]. Структурная схема метода приведена на Рис. 1 [2].

 

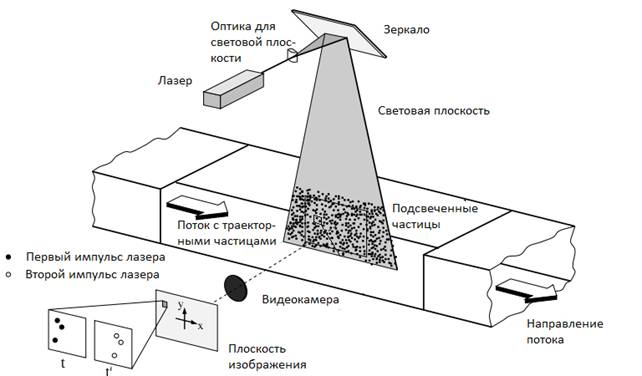
Рис.1. Структурная схема метода трассерной визуализации потоков.

При выборе метода анализа определяющую роль играет параметр, называемый оптической плотностью (ImageDensity) [2]. Он определяется средним числом частиц в области анализа.

Различают три основных значения оптической плотности. При малых значениях отдельные частицы хорошо различимы и можно легко сопоставить пары частиц на двух последовательных кадрах (Рис. 2а). В данном случае применяются так называемые траекторные методы анализа (ParticleTrackingVelocimetry – PTV). При средних значениях оптической плотности отдельные частицы еще можно различить, но сопоставить пары частиц на двух последовательных кадрах уже намного сложнее (Рис. 2б). В данном случае обычно применяется корреляционная обработка фрагментов изображения (ParticleImageVelocimetry – PIV). При больших значениях оптической плотности отдельные частицы на изображениях различить уже не удается (Рис. 2в). В данном случае анализируются картины лазерных спеклов (LaserSpeckleVelocimetry – LSV).
 

Рис. 2.  Три типа оптической плотности

Основным недостатком метода PTV является слишком малая плотность частиц, которая не позволяет отследить небольшие формирования в потоке. В методе LSV, напротив, плотность частиц слишком велика, что часто нежелательно с точки зрения динамики потока. Поэтому самое большое распространение на сегодняшний день получил метод PIV.

Основным достоинством метода PIVявляется его высокая надежность и повторяемость, особенно при низких отношениях сигнал/шум. Это достигается  благодаря статистической обработке изображений посредством корреляционного анализа. К тому же в результате получается регулярная сетка векторов, что облегчает последующую обработку векторного поля. Однако у данного метода есть свои недостатки. Во-первых, для получения одного вектора скорости необходимо 6-10 частиц, что снижает пространственное разрешение метода [3]. Во-вторых, корреляционный анализ очень чувствителен к различным оптическим искажениям.

Современное развитие техники и методов обработки позволяет с высокой точностью определять положение отдельных частиц на изображении, а так же их центр. И, хотя плотность частиц в методах траекторного анализа выбирается меньше, чтобы избежать перекрытия частиц, итоговое разрешение может оказаться даже выше, чем у метода PIV, так как в данном случае для определения одного вектора скорости нужна только одна частица.

Поэтому развитие методов выделения частиц для картин визуализации потоков, особенно в случае перекрытия изображения частиц, сегодня является очень актуальной задачей.Одному из таких методов посвящена данная статья.

Модель картины визуализации потоков

Для исследования алгоритмов обработки картин визуализации потоков необходима модель цифрового изображения. Хорошее описание подобной модели можно найти в [4]. Основная идея заключается в том, что сначала исходное непрерывное изображение сглаживается из-за усреднения по элементам матрицы фотоприемника, затем происходит дискретизация и квантование.

Исходное изображение в случае картин визуализации потоков представляет собой сумму частиц гауссовой формы с равновероятным положением частиц, равновероятной яркостью частиц и с небольшим разбросом размеров по нормальному закону [5].

Поэтому можно использовать следующую модель изображения:

- формат кадра N_x´N_y пикселов;

- каждая частица представляет собой двухмерную гауссову кривую; размер частиц был одинаковым по всему кадру и варьировался; яркость частиц была одинаковой; число частиц N_p; координаты частиц на первом кадре выбирали также по равномерному закону от 1 до N_x и до N_y по координатам x и у;

- к изображению добавлялся аддитивный нормальный шум с нулевым средним и различной дисперсией s².

Одинаковые размер и яркость частиц использовались для того, чтобы можно было использовать статистическую обработку результатов измерения.

 

Выделение частиц на основе поиска локальных максимумов

Данный метод заключается в сравнивание каждого пикселя изображения, который выше некоторого порога, с его ближайшими соседями и в случае максимума вычисляется его координата с подпиксельной точностью по следующей формуле [2]:

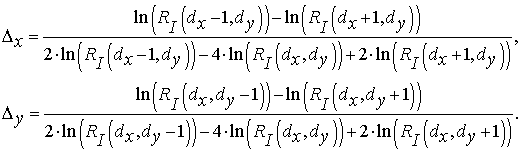
В данной формуле d_x и d_y–координаты максимума с точностью до пикселя, R_I–яркость изображения. Итоговые координаты максимума есть (d_x+Δ_x, d_y+Δ_y).

На Рис. 3 показан пример работы данного алгоритма.

 

Рис. 3.  Фрагмент бинаризированного изображения без шума (слева) и с шумом (справа) с нанесенными координатами, полученными с помощью метода локальных максимумов

Как видно из Рис. 3, при наличии шумов на изображении появляются ложные шумовые частицы. Так как шум на изображениях нестационарный, на последовательных кадрах координаты и количество данных шумовых частиц будет случайным, что полностью нарушит работу алгоритмов отслеживания частиц. Поэтому для того, чтобы избавиться от шумов, используют пороговую обработку изображения. У данного подхода есть один недостаток: из-за пороговой обработки пропадают не только шумы, но также и частицы, яркость которых меньше порога. Это приводит к снижению пространственного разрешения PTV-метода.

Маркерная градиентная сегментация по водоразделам

Конечной целью задачи сегментации является разбиение изображения на области. Понятие водораздела основано на представлении изображения как трехмерной поверхности, заданной двумя пространственными координатами и уровнем яркости в качестве высоты поверхности (рельефа). В такой интерпретации рассматриваются точки трех видов: (а) точки локального минимума; (б) точки, находящиеся на склоне, т.е. с которых вода скатывается в один и тот же локальный минимум; и (в) точки, находящиеся на гребни, т.е. с которых вода с равной вероятностью скатывается в более чем один локальный минимум. Множество точек, удовлетворяющих условию (б) называют водосборным бассейном локального минимума. Множество точек, удовлетворяющих условию (в) называют линиями водораздела [6].

Основная идея метода выглядит просто. Предположим, что в каждом локальном минимум проколото отверстие, после чего весь рельеф заполняется водой, равномерно поступающей снизу через эти отверстия, так что уровень воды всюду одинаков. Когда поднимающаяся вода в двух соседних бассейнах близка к тому, чтобы слиться вместе, в этом месте ставится перегородка, препятствующая слиянию. В конце концов, достигается фаза, когда над водой остаются видны только верхушки перегородок. Эти перегородки, соответствующие линиям водораздела, и образуют непрерывные границы, выделенные с помощью алгоритма сегментации по водоразделам [6].

Перед математическим описанием алгоритма сегментации сначала введем несколько определений. Пусть S – некоторое подмножество элементов изображения. Два его элемента, p и q называются связными в S, если между ними существует путь, целиком состоящий из элементов подмножества S. Для любого элемента p из S множество всех пикселей, связных с ним в S, называется компонентой связности (связной компонентой).

Переходим к описанию алгоритма. Пусть M₁, M₂,…,M_R – множества точек координатной плоскости, соответствующие локальным минимумам поверхности g(x, y). Обозначим через C(M_i) множество точек бассейна, отвечающего локальному минимуму  M_i. Обозначения min и max будем использовать для указания наименьшего и наибольшего значения изображения g(x, y). Наконец, запись T[n] означает множество точек (s, t), для которых g(s, t) < n. С геометрической точки зрения, T[n] есть множество точек, в которых поверхность g(x, y) лежит ниже плоскости g(x, y) = n.

При заполнении рельефа водой уровень поднимается в виде целочисленных приращений от n = min+1 до n = max + 1. В процессе подъема воды на любом шаге n алгоритму необходимо знать число точек, лежащих ниже уровня воды. Будем считать, что все точки множества T[n] отмечены черным цветом, а остальные – белым. Тогда при произвольном шаге подъема уровня воды, рассматриваемая трехмерная поверхность в проекции на плоскость xy может быть представлена двоичным изображением.

Пусть C_n(M_i) обозначает множество точек бассейна с локальным минимум M_i, которые оказались залиты на шаге n. Тогда C_n(M_i) можно рассматривать как двоичное изображение, задаваемое соотношением:

                                                                            

 Пусть теперь C[n] – объединение залитых водой частей всех бассейнов на шаге n:

                                                                                   

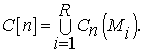
Тогда C[max+1] есть объединение всех имеющихся бассейнов. Можно показать [6], что при работе алгоритма никогда не происходит удаления элементов из множеств C_n(M_i) и T[n]. Таким образом, при увеличении n число элементов этих множеств либо возрастает, либо остается неизменным. Следовательно, C[n–1] является подмножеством C[n]. Согласно равенствам и , C[n] является подмножеством T[n], а значит и C[n–1] также есть подмножество T[n].

Алгоритм нахождения линий водораздела начинается с инициализации C[min+1] = T[min+1]. После этого алгоритм выполняется рекуррентно, предполагая на n-ом шаге множество C[n–1] уже построенным. Для получения множества C[n] из множества C[n–1] применяется следующая процедура. Пусть Q[n] – множество компонент связности множества T[n]. Тогда для каждой связной компоненты  есть три возможности:

а)  – пустое множество;

б)  содержит единственную компоненту связности множества C[n–1];

в)  содержит более одной компоненты связности множества C[n – 1].

Способ построения C[n] по C[n–1] зависит от того, какое этих из трех условий имеет место. Условие (а) означает, что встретился новый локальный минимум (начинается наполнение нового бассейна); в этом случае для построения множества C[n] компонента q добавляется к C[n–1]. Условие (б) имеет место, когда q лежит внутри бассейна некоторого локального минимума; в этом случае для построения множества C[n] компонента q также добавляется к C[n–1]. Условие (в) возникает, когда встретились точки гребня, разделяющего два или более бассейна. В этом случае дальнейший подъем воды привел бы к слиянию этих бассейнов, поэтому внутри связной компоненты q должна быть построена перегородка (или перегородки, если объединяются более двух бассейнов), не позволяющая бассейнам слиться вместе. После завершения работы алгоритма данные перегородки образуют лини водораздела.

Модуль градиента часто используется при предварительной обработке полутоновых изображений перед сегментацией по водоразделам. Пикселы изображения градиента с большими значениями располагаются вблизи границ объектов, а остальным участкам соответствуют нулевые значения пикселов. В идеале, выполняя преобразование водораздела, можно получить линии водоразделов вдоль границ объектов [6].

Однако непосредственное применение алгоритма сегментации по водоразделам градиента изображения обычно приводит к избыточной сегментации, вызванной шумом или другими локальными неоднородностями на градиентном изображении. Избыточная сегментация может быть настолько значительной, что сделает результат обработки практически бесполезным. Пример избыточной сегментации приведен на Рис. 4.

Рис. 4 Фрагмент картины визуализации потоков с нанесенными границами областей при избыточной сегментации (слева) и при нормальной сегментации (справа)

Практическое решение данной проблемы состоит в том, чтобы ограничить допустимое число областей путем включения в состав процедуры шага предварительной обработки, служащего для привнесения добавочной информации в процедуру сегментации. Подход, применяемый для устранения избыточной сегментации, основан на идее маркеров. Маркер представляет собой связную компоненту, принадлежащую изображению. Различают внутренние маркеры, относящиеся к интересующим нас объектам, и внешние маркеры, соответствующие фону изображения. Затем эти маркеры используются для подправления градиентного изображения [6].

В случае PIV-изображения можно использовать следующую процедуру определения маркеров. Градиент изображения имеет большое число локальных минимумов, что является причиной очень маленьких водосборных бассейнов. Большинство этих локальных минимумов очень мелкие и отображают маленькие детали, связанные с тепловым шумом видеокамеры и не играют роли в задаче сегментации. Чтобы их исключить, необходимо найти все низкие пятна на изображении, лежащие глубже некоторого заданного порогового уровня по сравнению с их ближайшим окружением. Это даст нам внутренние маркеры. После этого необходимо построить внешние маркеры, относящиеся к фону. Будем следовать подходу, при котором фон отмечается пикселями, которые расположены точно посередине между внутренними маркерами. Теперь, имея внутренние и внешние маркеры, используем их для модифицирования градиентного изображения с помощью так называемого минимального подъема [6]. Техника минимального подъема модифицирует полутоновое изображение так, что локальные минимумы достигаются только в отмеченных некой маской положениях. Другие величины пикселов повышаются для удаления всех прочих точек локального минимума. В качестве маски необходимо использовать логическое сложение внутренних и внешних маркеров.

Результаты моделирования

Во время моделирования использовались следующие параметры описанной выше модели:

N_x = N_y = 1024;

N_p = 10 000.

Дисперсия шума и размер частиц менялись. Для каждого значения на графике для статистической обработки использовалось по 20 смоделированных изображений.

На Рис. 5-7 приведены итоговые зависимости.

 

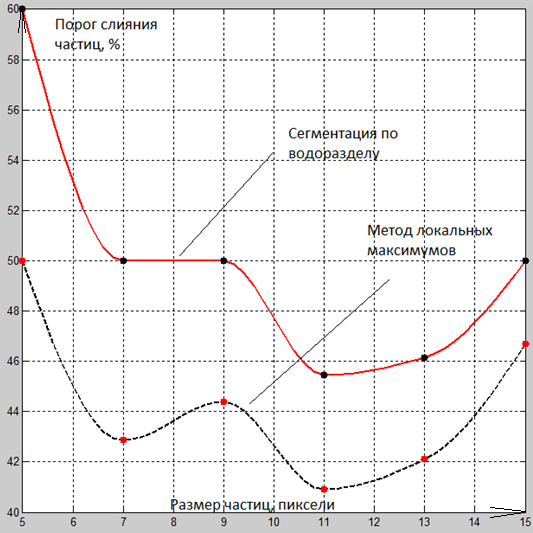
Рис. 5. Порог слияния частиц в зависимости от размера частиц

На Рис. 5 показаны пороги слияния частиц впроцентном соотношении от размера самих частиц. Шумов нет. Видно, что метод локальных максимумов проявляет себя лучше. К примеру, при размере частиц в 9 пикселей сегментация по водоразделам считает две частицы за одну, когда расстояние между ними 50% от их размера, а локальные максимумы разделяют частицы и при меньшем расстоянии между ними вплоть до 44.5 % от их размера.

 

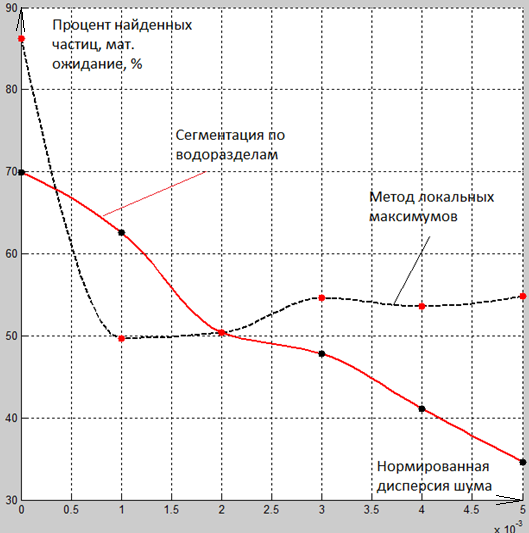
Рис. 6. Математическое ожидание процента найденных частиц в зависимости от дисперсии шума

 

На Рис. 6. показан процент определенных частиц в зависимости от дисперсии шума. Видно, что при отсутствии шума из-за того, что порог слияния у локальных максимумов ниже, процент определенных частиц у данного метода выше. Далее из-за противошумовой обработки происходит потеря информации, график резко падает и выходит на более-менее постоянный уровень. График определенных частиц для сегментации по водоразделам монотонно убывает, но не так резко, в результате чего образуется область, в которой процент определенных частиц у метода сегментации по водоразделам выше, чем у метода локальных максимумов.

 

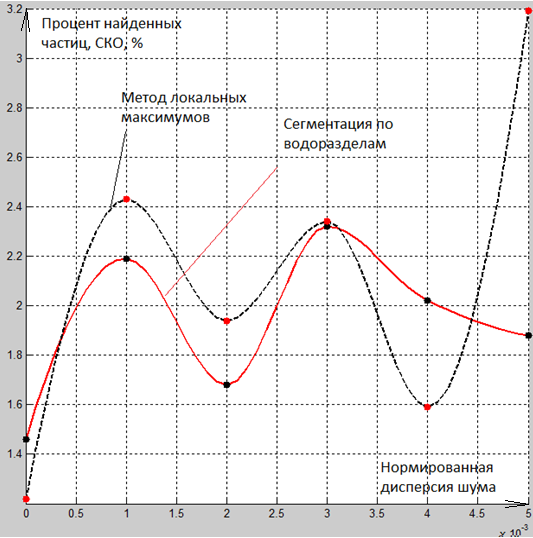
Рис. 7. Среднеквадратическое отклонение процента найденных частиц в зависимости от дисперсии шума

На Рис. 7 показаны аналогичные графики для СКО процента определенных частиц. В целом, оба метода ведут себя сходным образом, однако при больших шумах СКО в методе локальных максимумов начинает расти. Это связано с появлением ложных шумов частиц.

Выводы

Применение метода сегментации частиц по водоразделам позволяет при определенных значениях отношения сигнал/шум выделять на картинах визуализации потоков большее количество частиц, что повышает пространственное разрешение метода PTV. Кроме того, сегментация по водоразделам позволяет получить помимо координат частиц еще и некоторое представление о размерах самих частиц на изображении, что часто является важным параметром при оценке применимости того или иного алгоритма отслеживания частиц. Сегментацию частиц по водоразделам можно использовать совместно с другими методами сегментации, что позволит повысить надежность и точность определения координат частиц.

Дальнейшая задача при исследовании данного метода состоит в изучении оптимального размера частиц, на наличие которого указывает минимум в графике порога слияния частиц.

 

Литература

1. Ринкевичюс Б. С. Лазерная диагностика потоков /Под ред. В. А. Фабриканта. М.: Изд-во МЭИ, 1990.

2. Raffe M е. а. Particle image velocimetry. A Practical Guide, second edition. Berlin, Heidelberg, N.Y.: Springer, 2007.

3. Christian C., Kahler C. J. Cross-correlation or tracking – comparison and discussion. 16th IntSymp on Applications of Laser Techniques to Fluid Mechanics Lisbon, Portugal, 09-12 July, 2012

4. Б. Яне. Цифровая обработка изображений. М.: Изд-во Техносфера, 2007.

5. MarxenM., SullivanP. E., LoewenM. R. Jahne. Comparison of Gaussian particle center estimators and the achievable measurement density for particle tracking velocimetry // Experiments in Fluids – Vol. 29 – pp. 145-153, 2000.

6. Гонсалес Р., Вудс Р. Цифровая обработка изображений. М.: Изд-во Техносфера, 2005.