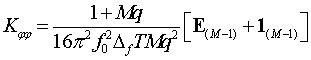УДК: 621.396.96
ТОЧНОСТЬ Оценки Пеленга ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ при нерегулярной структуре спектра в полосе анализа пассивной системы местоопределения
Т. Я. Шевгунов 1, А. В. Дубровин 2
1 – Московский авиационный институт («МАИ» НИУ)
2 – ЗАО «РАДИЙ ТН»
Статья получена 14 января 2014 г.
Аннотация. В настоящей работе рассматривается пассивная система определения местоположения источника радиоизлучения, состоящая из узкобазовых подсистем, реализуемых взаимно когерентными кольцевыми антенными решётками; оценивание проводится с использованием оптимального одноэтапного алгоритма. В работе исследуется следующий вопрос: насколько уменьшается точность оценки пеленга по сравнению с нижней границей Крамера-Рао при условии произвольного расположения гармонических составляющих сигнала в полосе анализа пеленгационной системы для случая гауссовского случайного процесса. Проведенное имитационное статистическое моделирование позволило определить величину расхождения СКО, полученного по результатам моделирования, с СКО для случая равномерного спектра, для которого имеются описанные в литературе аналитические выражения потенциальной точности в явном виде. Также посредством моделирования в работе проводится исследование влияние предварительной оконной фильтрации сигнала со случайной структурой спектра на точность оценки пеленга: рассмотрены часто применяемые в спектральном анализе оконные функции и проведен сравнительный анализ характеристик точности определения местоположения в зависимости от отношения сигнал/шум на входе приёмника для каждой из них. Основные результаты доложены на 7-й Всероссийской конференции «Радиолокация и радиосвязь», Москва, ИРЭ им. В.А.Котельникова РАН, 2013 г.
Ключевые слова: пассивная радиолокационная система, угломерный метод, кольцевые антенные решетки, одноэтапные процедуры оценивания.
Abstract. This paper deals with the angle-of-arrival passive location system consisting of mutually coherent circular antenna arrays implementing one-step maximum likelihood based estimation procedure. The question raised in the present paper is accuracy degradation due to the arbitrary positions of spectral components in the locator receiver bandwidth in comparison with Cramer-Rao Lower Bound for the case of Gaussian random radio emission. The well-known expression of angle estimator accuracy in the case of band-uniform spectrum is compared to the results obtained by the numerical statistical modeling; this allows one to evaluate the deterioration of the accuracy due to arbitrary positioned spectral components. The numerical modeling also provides the discussion for preliminary time-window filtration of the received signals in order to increase the accuracy of angle estimator. Thus it was shown that the common used windows such as Hann, Bartlett and Keiser-Bessel can be useful in the case of sparse arbitrary spectrum.
Keywords: passive locator, angle-of-arrival, circular antenna arrays, one-step maximum likelihood estimation.
Постановка задачи
В настоящее время остаётся актуальной научно-техническая проблема создания специализированного класса систем, решающих задачу определения местоположения технических объектов в интересах частных компаний и государственных служб. Одно из типичных требований, предъявляемых к таким системам, заключается в том, что оценивание местоположения должно проводиться по электромагнитным излучениям, создаваемым объектами в процессе их функционирования в штатном режиме или с использованием уже размещенного на них радиопередающего оборудования. Причиной этого требования часто оказывается то, что такие объекты не могут быть оборудованы специальными передатчиками дополнительных сигналов вследствие удорожания их разработки и эксплуатации, требований электромагнитной совместимости, стандартов технической или служебной безопасности или в силу каких-либо других ограничений.
Современные пассивные системы определения местоположения объекта представляют собой распределенные программно-аппаратные комплексы, осуществляющие приём электромагнитного излучения объектов-источников и его последующую обработку. Ключевым элементом программно-аппаратного комплекса, составляющим математическое обеспечение системы определения местоположения, является алгоритм оценивания. Одним из возможных признаков для классификации алгоритмов оценки местоположения является количество этапов – число последовательно осуществляемых шагов оценивания, при которых оценки, полученные на некотором этапе, служат в качестве исходных данных для проведения последующего этапа. Отличительная особенность одноэтапного алгоритма состоит в том, что его решающая функция подлежит максимизации в пространстве величин, непосредственно оцениваемых в задаче в то время, как в многоэтапных методах решающая функция составляется относительно промежуточных физически значимых величин, а окончательное решение ищется, как правило, приближением по методу наименьших квадратов. При общих допущениях [1] считается, что при больших отношениях сигнал/шум потенциальная точность одноэтапного и многоэтапного алгоритмов одинакова. При малых отношениях сигнал/шум (типично, 0 дБ и меньше) оценки одноэтапных и многоэтапных алгоритмов различаются.
В настоящей работе рассматривается задача оценки пеленга, угла направления на объект, формируемого одноэтапным оптимальным алгоритмом единственной узкобазовой системой, рассмотренной в работе [2], на основе измерений электромагнитного излучения, выполняемых взаимно-когерентной кольцевой антенной решеткой. В работе принята двумерная модель размещения объекта и станции, что соответствует практическому случаю, когда источник радиоизлучения (ИРИ) и приёмная станция находятся на поверхности земли. Реализация такой системы описывается типичной радиотехнической схемой организации программно-аппаратного комплекса, в которой сигнал, принимаемый каждым элементом антенной системы базовой станции, подвергается квадратурной демодуляции. Комплексная огибающая принятого сигнала, снятая с центральной частоты переводится посредством аналого-цифрового преобразователя в цифровую форму, и дальнейшая обработка, конечной целью которого является вычисление искомого угла, проводится в цифровом микропроцессоре с использованием алгоритмов цифровой обработки сигналов.
При выводе оптимальных алгоритмов в исследованиях делается предположение о том, что излучаемый сигнал представляет собой стационарный гауссовский случайный процесс со спектральной плотностью мощности, спектральные составляющие которой одинаковы и расположены в полосе анализа с равномерным шагом, равным 1/T (где T – длительность интервала наблюдения) [3]. Сигнал, измеряемый в точках приёма, представляет собой аддитивную смесь излучаемого сигнала (с учётом линейного ослабления в процессе распространения) и гауссовского шума, равномерного в полосе анализа. Делаются предположения о некоррелированности излучаемого сигнала и шума в каждой точке приёма и об отсутствии взаимной корреляции между шумами измерения в различных точках приёма. Принимаемый сигнал обладает узким спектром, сосредоточенным в окрестности центральной частоты, таким, что различием фаз его спектральных составляющих, обусловленных временем распространения можно пренебречь по сравнению с прочими факторами. Также фронт электромагнитный волны, сформовавшийся у приемной антенной системы, полагают плоским.
Совокупность перечисленных допущений позволяют, во-первых, построить наиболее простой с вычислительной точки зрения алгоритм оценивания, во-вторых, при выборе параметров системы на этапе её проектирования опираться на аналитические выражения потенциальной точности, записанные в компактной форме.
В настоящем исследовании проводится анализ влияния фактической структуры спектра излучаемого сигнала в полосе анализа. Такое исследование, проведенное на основе имитационного моделирования, позволит принять решение о целесообразности модификации алгоритма в случае, если спектр имеет нерегулярную структуру.
Потенциальная точность пеленгатора
Потенциальная точность определяется неравенством Крамера-Рао, которое для оценки пеленга может быть записана посредством выражения [4]:
![]() (1)
(1)
в котором матрица Kjj выражается через параметры: центральную частоту спектра f0, ширину его спектра 2Δf, длительность интервала наблюдения T, отношение сигнал шум q – следующим образом:
где E(M−1) и 1(M−1) – соответственно единичная матрица и квадратная матрица, составленная из единиц, размера (M–1)×(M–1). Элементы вектора B, определяющего трансформацию параметров матрицы Фишера, вычисляются через разности координат приёмных элементов антенной системы (xm, ym):
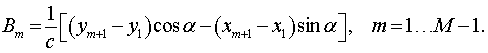 (3)
(3)
При построении фазовых пеленгаторов высокой технологичностью обладает решение, при котором приемная система организуется на основе кольцевых антенных решеток, представляющих собой набор антенных элементов, расположенных регулярно на одной окружности или нескольких концентрических окружностях различного радиуса.
Для случая антенны, состоящей из единственного кольца с числом элементов M с дополнительным центральным элементом, выражение потенциальной точности примет вид [5]:
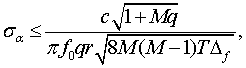 (4)
(4)
где число элементов M выбирается простым числом [6]: в настоящем исследовании M = 7.
Имитационное моделирование
На рис. 1 представлено относительное расположение источника излучения и приемной станции, в которой используется приемная система из семиточечной кольцевой антенной решетки радиуса r = 0,6 м и центрального элемента.
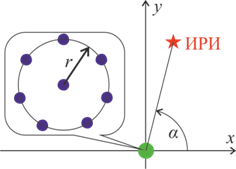
Рис. 1. Взаимное расположение источника радиоизлучения
(ИРИ) и приёмной базовой станции.
Для проведения моделирования были выбраны следующие параметры: центральная частота f0 = 50 МГц, ширина спектра 2Δf = 32 кГц, длительность интервала наблюдения T = 1 мс. Таким образом, число спектральных составляющих, по которым будет производиться оценивание, равно N = 2TΔf = 32. Среднеквадратическая ошибка может быть вычислена по формуле:
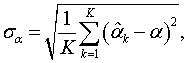 (5)
(5)
где α – истинное
значение пеленга, а ![]() – оценка пеленга, полученная в k-том эксперименте; число экспериментов в проведенном
исследовании K = 10 000.
– оценка пеленга, полученная в k-том эксперименте; число экспериментов в проведенном
исследовании K = 10 000.
На рис. 2 представлен график зависимости точности оценки пеленга от отношения сигнал/шум, полученный в результате имитационного моделирования; график дополнен кривой теоретической границы Крамера-Рао. Из анализа графика можно сделать заключение, что для отношений сигнал/шум больших –5 дБ результаты моделирования оптимального алгоритма практически точно ложатся на границу точности, для меньших отношений сигнал шум результаты расходятся.
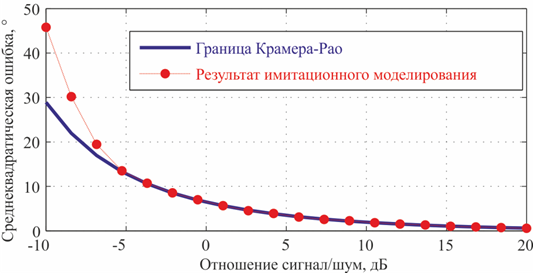
Рис. 2. Точность оценивания (СКО) пеленга оптимальным одноэтапным
алгоритмом
граница Крамера-Рао и результат имитационного моделирования.
Рассмотрим ситуацию, когда случайный процесс, создаваемый источником радиоизлучения, в полосе анализа будет состоять из такого же числа, а именно: 32, гармонических составляющих, но расположенных случайно в полосе анализа.
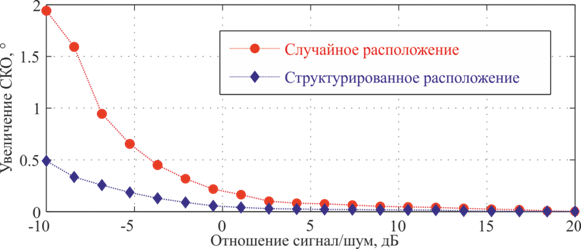
Значение частоты для каждой гармонической составляющей выбиралось путём генерации случайного числа, имеющего равновероятное распределение по всей полосе анализа, независимо от других составляющих спектра. Рис. 3 качественно иллюстрирует регулярное расположение гармонических составляющих в полосе анализа (рис.3, а) и случайное расположение (рис. 3, б). Во втором случае вид графика зависимости точности оценки будет в целом аналогичен графику на рис. 2, поэтому больший практический интерес представляет ухудшение точности при таком хаотическом расположении гармоник по сравнению с регулярным. Разность значений среднеквадратических ошибок для излучаемых сигналов с хаотическими и регулярными спектрами представлена на рис. 4. Из данного графика, следует, что увеличение ошибки, обусловленное хаотическим расположением гармонических составляющих, составляет небольшую долю от среднеквадратической ошибки, обусловленной присутствием аддитивного шума.
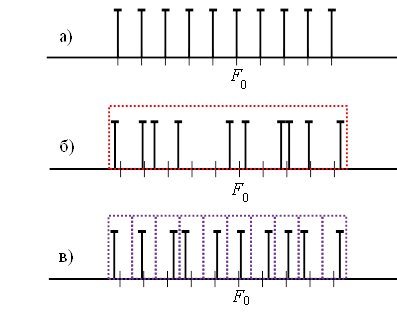
Рис. 3. Структура спектра излучаемого сигнала: а) –
регулярная, б) – случайная с равновероятным распределением
каждой составляющей
в полосе анализа, в) – структурированная случайная, при которой каждая
составляющая
случайно размещена в пределах частотного интервала.
Рассмотрим ещё один вид структуры спектра, промежуточный между регулярным и случайным, когда спектру принимаемого сигнала присуща некоторая структурированность. Будем считать, что диапазон частот анализа можно разбить на равномерные отрезки протяженностью 1/T, центром каждого из которых будет частота, в которой производится оценивание спектра ДПФ. Положим, что в каждом из таких интервалов расположена только одна спектральная составляющая, при этом её позиция в пределах своего отрезка подчиняется равномерному распределению, а позиции величин в пределах различных отрезках – взаимно независимые случайные величины. Этот случай иллюстрируется рис. 3, в. Увеличение среднеквадратической ошибки оценки пеленга при использовании спектра подобной структуры также представлено на рис. 4. Необходимо отметить, что модель, структурирующая спектр подобным образом, приводит к дополнительной ошибке примерно в четыре раза меньшей, чем при равномерном размещении составляющих во всей полосе анализа.
|
|
Теперь рассмотрим случай, когда число гармонических составляющих сигнала ИРИ, фактически попадающих в полосу анализа 2Δf , окажется существенно меньше, чем число точек спектра ДПФ, по которым будет производиться оценивание. В случае, когда известные позиции этих составляющих расположены на частотах, кратных шагу анализа по частоте 1/T, уменьшение точности можно рассмотреть как эквивалентное сокращение полосы анализа; для этого будет достаточно заменить в формуле (2) произведение 2TΔf на фактическое число составляющих по которым производится оценка. Однако в случае, когда структура спектра не обладает описанной регулярностью, выбор частотных позиций, в которых необходимо проводить оценивание оказывается нетривиальной задачей.
Для иллюстрации этого рассмотрим пример единственной гармонической составляющей, расположенной на частоте –0,5 кГц , т.е. ровно посередине между 16 и 17 отсчётами спектра, определяемого посредством ДПФ. Такое расположение отвечает наименее благоприятному случаю распределения спектра по частотам анализа. На рис. 5 представлена зависимость точности оценки пеленга от отношения сигнал/шум при проведении обработки с использованием всех отсчётов полосы анализа.
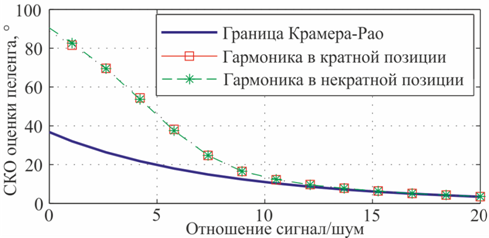
Рис. 5. Результаты моделирования точности оценки гармонической составляющей,
расположенной в кратной и некратной позиции.
Для сравнения приведена граница
Крамера-Рао для гармоники в кратной позиции.
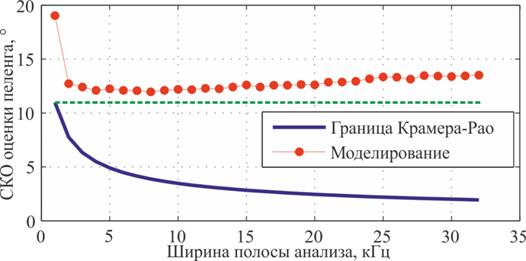
Рис. 6. Точность оценивания (СКО) пеленга оптимальным алгоритмом в зависимости от ширины
используемой полосы для фактически единственной гармоники. Зелёная пунктирная
линия – граница Крамера-Рао для оценки по единственной гармоники в кратной
позиции.
Теперь проанализируем для отношения сигнал/шум равного 10 дБ зависимость точности от числа спектральных отсчётов, используемых для оценивания. График этой зависимости представлен на рис. 6, из представленного графика следует, полосу анализа необходимо сокращать, несмотря на явление утечки спектральных компонент ДПФ.
В качестве ad hoc решения способного улучшить ситуацию рассмотрим предварительную оконную фильтрацию. Результаты для некоторых окон представлены в таблице 1, результаты получены усреднением 10 000 экспериментов при отношении сигнал/шум 10 дБ. При этом оценивание пеленга проводилось по единственному отсчёту спектра, соответствующему гармонической составляющей на центральной частоте.
Таблица 1. Точность оценки пеленга (СКО) при использовании некоторых типов оконных функций.
|
|
Тип окна |
СКО
оценки пеленга, ° |
|
|
Некратное положение |
Кратное положение |
||
|
1 |
Прямоугольное |
19,4 |
11,1 |
|
2 |
Ханна (косинусное) |
16,2 |
13,1 |
|
3 |
Бартлетта (треугольное) |
17,1 |
14,6 |
|
4 |
Кайзера-Бесселя (β = 3) |
16,8 |
12,1 |
|
5 |
Кайзера-Бесселя (β = 1) |
18,9 |
11,2 |
Заключение
Проведенное в настоящей работе исследование частного вопроса влияния структуры спектра на точность оценки пеленга на источник радиоизлучения позволяет выработать следующие рекомендации по модификации алгоритма оценивания. Доклад по результатам данного исследования был представлен на профильной секции всероссийской конференции «Радиолокация и радиосвязь» [7].
В том случае, если число спектральных составляющих велико – их количество сопоставимо с числом отсчётов спектра ДПФ – потери в точности, обусловленные их случайным расположением, невелики: для малых отношений сигнал/шум они составляют менее 10% и их доля падает с увеличением самого отношения сигнал/шум. Малая доля вклада этих потерь объясняется тем, что при большом числе спектральных составляющих на каждой частоте анализа формируется сумма отдельных компонент. Таким образом, имеет место эффект нормализации, и полученный спектр может быть рассмотрен как многомерный комплексный вектор с гауссовским распределением; и для него будут, в общем, справедливы исходные предпосылки модели. Как следствие, в большинстве практических задач алгоритм оценивания не потребует корректив или введения дополнительных шагов.
Если число излучаемых спектральных составляющих в полосе анализа мало, а их расположение не является регулярным, то потери по отношению к регулярному расположению будут составлять заметную долю. Так в наихудшем случае единственной гармоники, расположенной в позиции некратной шагу ДПФ, среднеквадратическая ошибка может увеличиться в 1,6 раз. В таком случае целесообразным оказывается применение предварительной обработки на основе взвешивающих окон, из которых наибольший выигрыш дают окна Ханна, Бартлетта и Кайзера-Бесселя.
Литература
1. Черняк В. С. Многопозиционная радиолокация. – М.: Радио и связь, 1993.
2. Дубровин А. В., Сосулин Ю. Г. Одноэтапное оценивание местоположения источника радиоизлучения пассивной системой, состоящей из узкобазовых подсистем // Радиотехника и электроника, 2004, т. 49, № 2, с. 156–170.
3. C. H.Knapp, G.C. Carter, The Generalized Correlation Method for Estimation of Time Delay, IEEE Transaction on Acoustic, Speech and Signal Processing, 1976, vol. 24, No. 4, p. 320–327.
4. Дубровин А.В. Одноэтапные процедуры и пассивные системы определения координат источников радиоизлучений: автореферат диссертация на соискание учёной степени доктора технических наук: 05.12.14. – Москва, 2007.
5. Дубровин А.В. Потенциальная точность пеленгования комплексами с антенными решетками, имеющими конфигурацию в виде набора произвольного числа колец // Радиотехника и электроника, 2006, т. 51, № 13, с. 268-270.
6. Дубровин А.В. Выбор оптимальной конфигурации антенной решетки, размещаемой на мачте, в мобильном комплексе пеленгования ОВЧ-УВЧ-диапазонов (20-3000 МГц) // Антенны, 2005, № 7-8, с. 49–52 .
7. Шевгунов Т.Я. Влияние структуры спектра излучаемого сигнала на точность оценки направления на источник радиоизлучения // VII Всероссийская конференция «Радиолокация и радиосвязь», ИРЭ РАН, 2013, с. 35–39.