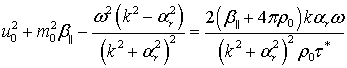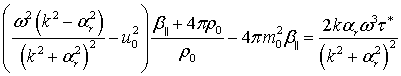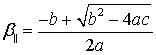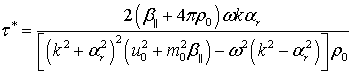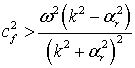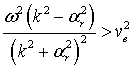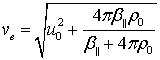УДК 53.098, 538.955
влияние релаксации магнитного поля на всплеск коэффициента поглощения ультразвука в магнитной наножидкости emg – 605
И. Э. Овчинников
Московский государственный университет приборостроения и информатики
Статья получена 16 января 2014 г.
Аннотация. Проведен теоретический анализ экспериментальных данных для скорости и коэффициента поглощения ультразвука в магнитной жидкости на основе воды при воздействии однородного постоянного магнитного поля с величиной от нескольких до 120 кА/м. Показано, что всплеск коэффициента поглощения ультразвука можно объяснить при помощи процесса релаксации магнитного поля к своему равновесному значению в магнитной жидкости. Для магнитных полей от 30 кА/м до 120 кА/м подтверждена теоретическая зависимость: параметр магнитоупругости обратно пропорционален дифференциальной магнитной восприимчивости.
Ключевые слова: магнитная наножидкость, магнитные наночастицы, магнетит, магнитное поле, ультразвук.
Abstract: The theoretical analysis was made on the experimental data for the ultrasonic velocity and absorption coefficient in water-based magnetic nanofluid EMG – 605 when exposed to a homogeneous static magnetic field with a magnitude from a few and up to 120 kA/m. It was shown, that the ultrasonic absorption coefficient splash can be explained by a process of relaxation of the magnetic field to its equilibrium value in a magnetic fluid. For magnetic fields from 30 kA/m and up to 120 kA/m the theoretical dependence is confirmed: the magnetoelasticity parameter is inversely proportional to the differential magnetic susceptibility.
Keywords: magnetic nanofluid, magnetic nanoparticles, magnetite, magnetic field, ultrasonics.
1. Введение
Магнитные жидкости находят практическое применение в машиностроении для создания уплотнительных устройств, уменьшения трения, гибкой передачи усилий. В радиотехнике они могут представлять интерес для управляемых магнитным полем поглотителей и регуляторов. Приложение постоянного магнитного поля существенным образом влияет на распространение ультразвука в магнитной жидкости. Исследованию данного явления и посвящена настоящая статья. В работе [1] приведена система уравнений, которая описывает магнитную жидкость при учете процесса релаксации магнитного поля к своему равновесному термодинамическому значению. Магнитная жидкость состоит из жидкости-носителя (вода, додекан, керосин и др.), магнитных частиц и небольшой добавки поверхностно-активного вещества. В настоящее время принято, что магнитная наножидкость – это магнитная жидкость, в которой все магнитные частицы являются магнитными наночастицами [2]. В основном, используют магнитные наночастицы из магнетита. На поверхностях данных частиц образуется оболочка из молекул поверхностно-активного вещества, что препятствует слипанию магнитных наночастиц. Благодаря этому, магнитные наножидкости являются устойчивыми и не коагулируют. Толщина оболочки из молекул поверхностно-активного вещества может зависеть и от жидкости-носителя: в основном, магнитные наночастицы покрыты одним слоем ПАВ. Но, в частности, в магнитных наножидкостях на основе воды магнитные наночастицы покрыты двумя слоями ПАВ [2]. Воздействие магнитного поля сильно влияет на движение магнитных наночастиц, но магнитная наножидкость устойчива и является сплошной средой для процесса распространения ультразвука малой амплитуды. Значит, магнитное поле может влиять на упругость магнитной наножидкости, что подтвеждено изменением скорости ультразвука в экспериментах [2]. В работе [3] были одновременно измерены скорость и коэффициент поглощения ультразвука в магнитной наножидкости EMG – 605 при воздействии различных величин магнитного поля. Значения коэффициента поглощения ультразвука при малых величинах магнитного поля и при напряженности магнитного поля около 120 кА/м равны в пределах точности эксперимента. На интервале от 30 до 50 кА/м проявляется всплеск коэффициента поглощения ультразвука: увеличение на 21% (рис. 3 [3]), что довольно много. Целью настоящей работы является объяснение данного всплеска при помощи процесса релаксации магнитного поля к своему равновесному значению.
2. Теоретический анализ экспериментальных данных по распространению ультразвука в магнитной наножидкости EMG – 605
В работе [4] было рассмотрено
распространение звука в магнитных жидкостях параллельно внешнему однородному
стационарному магнитному полю согласно теоретическим положениям о релаксации
магнитного поля к своему равновесному значению [1,2]. В [3] получены экспериментальные
данные по скорости и коэффициенту поглощения для распространения ультразвука
тоже параллельно внешнему однородному стационарному магнитному полю. В [4]
распространение ультразвука описывается дисперсионным уравнением для быстрой магнитогидродинамической
волны, из которого следует система двух действительных уравнений для двух
неизвестных параметра магнитоупругости 
и
времени релаксации магнитного поля 
:
|
|
|
(1) |
где 
– равновесное
значение плотности магнитной жидкости, 
–
равновесное значение удельной намагниченности магнитной жидкости, 
– круговая частота ультразвука, 
– волновое число, 
, 
– коэффициент поглощения ультразвука в магнитной
жидкости при воздействии однородного постоянного магнитного поля, 
– коэффициент поглощения ультразвука в магнитной жидкости без воздействия
внешнего магнитного поля, 
– скорость ультразвука в магнитной
жидкости при воздействии однородного постоянного магнитного поля, 
– скорость ультразвука в магнитной жидкости без воздействия внешнего магнитного
поля.
Из системы (1) получаются
выражения для и :
|
|
(2) |
|
|
(3) |
где
,
,
.
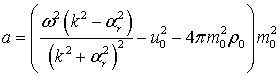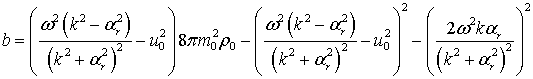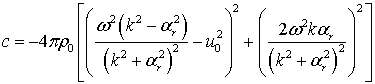Для применения формул (2-3) необходимо выполнение двух строгих неравенств:
|
|
(4) |
|
|
|
(5) |
где скорость быстрой магнитозвуковой волны в идеальной магнитной жидкости с вмороженной намагниченностью равна [2]:
|
|
(6) |
скорость магнитогидродинамической волны в идеальной магнитной жидкости с равновесной намагниченностью равна [5]:
|
|
|
(7) |
В работе [3] использовалась магнитная
жидкость на основе воды EMG – 605,
которая является магнитной наножидкостью, т.к. средний диаметр частиц магнетита
равен 
нм, а плотность равна 
г/см3. Образец магнитной
жидкости находился в измерительной ячейке при температуре 
C. Результаты в [3] были получены при частоте ультразвука 
МГц. На рис. 3 [3] находятся 13
экспериментальных точек для скорости и 13 экспериментальных точек для
коэффициента поглощения ультразвука в зависимости от 13 значений напряженности
магнитного поля, которое изменялось от нескольких до 120 кА/м.
Значение удельной намагниченности вычислялось по формуле [2]
,
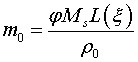где 
–
объемная доля магнитных наночастиц [3], 
Гс –
намагниченность насыщения магнетита, 
– функция Ланжевена, 
, 
– средний объем магнитной наночастицы, 
– константа Больцмана, 
– температура магнитной наножидкости [3].
Значения напряженности магнитного поля 
, скорости
и коэффициента поглощения ультразвука определялись
из рис. 3 [3] для каждой экспериментальной точки.
При проведении расчетов было
установлено: если напряженность магнитного поля менее 30 кА/м, то вычисленные
значения и чувствительно зависят от численных
значений скорости звука и коэффициента поглощения в магнитной жидкости без воздействия внешнего магнитного поля. Поэтому
на рис. 1-4 изображены по два графика: 1) треугольниками и 2) кругами, т.к. в первом
случае были применены значения 
см/с и 
см-1, которые были вычислены из экспериментальных данных рис. 3 [3] при помощи экстраполяции, а во втором – были равны значениям 
см/с и 
см-1 при самом малом значении
напряженности магнитного поля. Поэтому в другом случае получилось 12 значений,
т. е. на одну точку меньше на каждом рисунке.
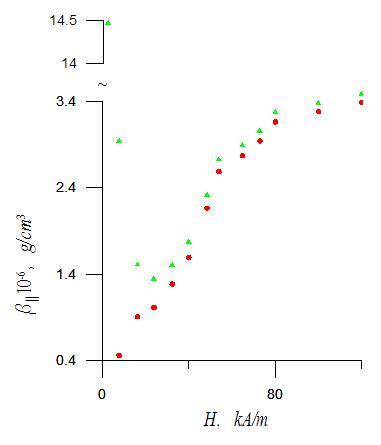
Рис. 1. Зависимость
параметра магнитоупругости от напряженности
магнитного поля по формуле (2) и экспериментальным данным [3].
Во втором случае (круги) на рис. 1 зависимость от напряженности магнитного поля может
быть приближенно объяснена при помощи производной функции Ланжевена по напряженности
магнитного поля . При напряженностях магнитного
поля более 50 кА/м вычисленные значения и для двух случаев практически совпадают. Численные расчеты показали, что
строгие неравенства (4-7) верны для каждой экспериментальной точки.
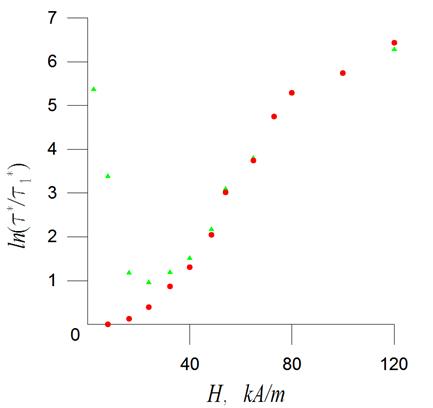
Рис. 2. Зависимость натурального логарифма относительного времени релаксации от напряженности магнитного поля по формуле (3) и экспериментальным данным [3].
На рис. 2 показана
зависимость 
от напряженности магнитного поля, где – время релаксации для каждого значения напряженности магнитного поля в
экспериментах, а 
секунды – время релаксации для
первой точки (круги), которая является второй экспериментальной точкой. Магнитная
наножидкость является сложной системой, поэтому время релаксации магнитного
поля к своему равновесному значению может зависеть от многих параметров, и от
условий проведения эксперимента. Время релаксации при напряженности магнитного
поля 120 кА/м достигает около двух с половиной минут рис. 2, что приблизительно
равно времени установления стабильного сигнала ультразвука при данных значениях
магнитного поля. В одной из пионерских работ [6] было показано, что время
установления стабильного сигнала ультразвука в магнитной жидкости зависит от
величины магнитного поля и может составлять почти минуту. В экспериментах [7]
ждали несколько минут установления стабильного сигнала ультразвука. Вполне
логично, что если поле намагниченности вморожено в вещество, тогда данные
времена могут быть одного порядка.
На рис. 3 показано, что
скорость быстрой магнитозвуковой волны в идеальной магнитной жидкости с
вмороженной намагниченностью (4) превышает экспериментальные значения скорости ультразвука
для каждой точки. Является интересным, что максимум этого превышения
находится около 38-42 кА/м, что близко к максимуму всплеска коэффициента
поглощения ультразвука в экспериментальных данных на рис. 3 [3].
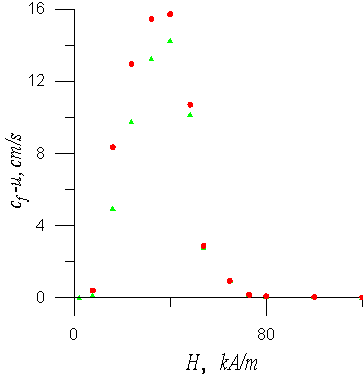
Рис. 3. Зависимость разности между скоростью по формуле (6) и скоростью ультразвука в магнитной жидкости по экспериментальным данным [3] от напряженности магнитного поля.
В работах [2,4,5,8] являлся подгоночным параметром при
сравнении теоретических расчетов с экспериментальными данными. В работе [8] было показано, что для данного параметра
верна теоретическая зависимость 
.
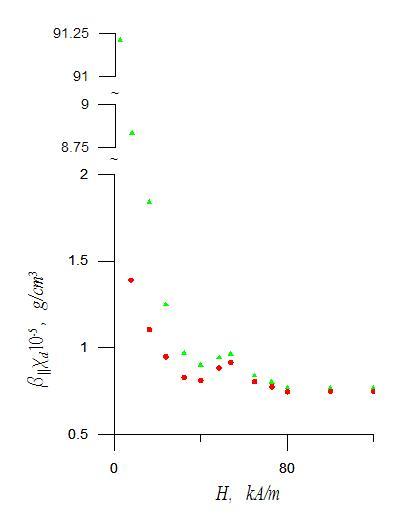
Рис. 4. Зависимость произведения параметра
магнитоупругости на дифференциальную магнитную
восприимчивость 
от напряженности магнитного
поля по формуле (2) и экспериментальным данным [3,9].
На рис. 4 показана зависимость
произведения параметра магнитоупругости на дифференциальную магнитную восприимчивость
от напряженности магнитного поля.
Значения взяты из рис. 1. Экспериментальные
значения дифференциальной магнитной восприимчивости 
были
взяты из рис. 1 [9]. Эта величина изменяется в диапазоне: для первой точки на
рис. 3 [3] при самом малом значении магнитного поля 
, а при
напряженности магнитного поля 120 кА/м 
.
Результаты в [9] были получены
для этой же магнитной наножидкости EMG – 605
при другой частоте ультразвука 3.6 МГц, но зависимость от величины магнитного поля
может быть одинаковая для разных частот. На рис. 4 очевидно, что произведение становится практически постоянным при значениях
напряженности магнитного поля от 30 кА/м до 120 кА/м. Данный результат
подтверждает теоретическую зависимость .
3. Выводы
Итак, в настоящей статье
показано, что теоретические положения работ [1,2] позволяют объяснить всплеск
коэффициента поглощения ультразвука в магнитной наножидкости EMG – 605 при помощи процесса релаксации
магнитного поля к своему равновесному значению. На интервале для напряженности
магнитного поля от 30 кА/м до 120 кА/м с хорошей точностью вычисляется
теоретический параметр магнитоупругости . При
значениях напряженности магнитного поля менее 30 кА/м наблюдается некоторая
двойственность при определении данного параметра. Данные вопросы могут быть
исследованы в новых экспериментах по воздействию магнитного поля на магнитные наножидкости.
Литература
[1] V.V. Sokolov, V.V. Tolmachev, “Propagation of Shear Waves in a Magnetic Liquid with Frozen-in Magnetization”, // Tech. Phys. Lett. 1997. Vol. 23, No. 1 p. 5-6. DOI: 10.1134/1.1261628
[2] V.V. Sokolov, “Wave Propagation in Magnetic Nanofluids (A Reiew)”, // Acoustical Physics. 2010. Vol. 56. No. 6. p. 972-988. DOI : 10.1134/S1063771010060229
[3] T. Hornowski, “Ultrasonic Properties of EMG-605 Magnetic Liquid”, // Proc. of SPIE. 2005. Vol. 5828. p. 205-212. http://dx.doi.org/10.1117/12.612810
[4] И.Э. Овчинников. Влияние постоянного магнитного поля на распространение ультразвука в магнитных жидкостях. // Журнал радиоэлектроники: электронный журнал. 2013. N1. URL: http://jre.cplire.ru/jre/jan13/12/text.pdf
[5] I.E. Ovchinnikov, V.V. Sokolov, “Waves in Magnetic Fluids with Equilibrium and Frozen-In Magnetizations”, // Acoustical Physics, 2013. Vol. 59, No. 1, p. 51-55. DOI: 10.1134/S1063771012060115
[6] A.V. Narasimham, “Direct Observation of Ultrasonic Relaxation Times in Ferrofluids under the Action of a Magnetic Field”, // Indian J. Pure & Appl. Phys. 1981. Vol. 19. No. 11. p. 1094-1097.
[7] M. Motozawa, Y. Matsumoto and T. Sawada, “Properties of Ultrasonic Propagation in Functional Fluids under Magnetic Fields”, // Int. J. Modern Phys. B 2007. Vol. 21. Nos. 28-29. p. 4914-4921.
[8] V.V. Sokolov, V.V. Tolmachev, Anisotropy of Sound Propagation in a Magnetic Fluid // Acoustical Physics. 1997. Vol.43. No. 1. p.92-95.
[9] A. Skumiel, A. Jozefczak, T. Hornowski, M. Kaczmarek, “The Effect of the Concentration of Ferroparticles in a Magnetic Fluid on its Acoustic and Magnetic Properties”, // Molecular and Quantum Acoustics. 2002. Vol. 23. p. 389-396.