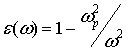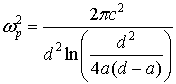УДК 535.63, 537.874
ЭФФЕКТИВНЫЕ ЭЛЕКТРОФИЗИЧЕСКИЕ СВОЙСТВА МЕТАЛЛИЧЕСКИХ ЭЛЕКТРОМАГНИТНЫХ КРИСТАЛЛОВ
А. Ю. Ветлужский
Институт физического материаловедения СО РАН
Статья получена 13 ноября 2014 г.
Аннотация: Рассмотрены различные методы определения эффективной диэлектрической проницаемости двумерных электромагнитных кристаллов, состоящих из тонких проводящих цилиндров. Проанализированы причины расхождения результатов, полученных по разным методикам. Указаны общие трудности применения данных подходов к описанию свойств пространственно ограниченных структур.
Ключевые слова: электромагнитные кристаллы, запрещенная зона, эффективный показатель преломления, плазменная частота.
Abstract: Different methods to determining the effective permittivity of two-dimensional electromagnetic crystals consisting of thin conducting cylinders is considered. The causes of discrepancies between the results obtained by different methods is analyzed. Common problems of these approaches to the description of the properties of spatially confined structures is discussed.
Keywords: electromagnetic crystals, effective refractive index, stop-band, the plasma frequency.
Электромагнитными или фотонными кристаллами принято называть периодические структуры, обладающие способностью подавлять распространение через них электромагнитных излучений в определенных частотных диапазонах, называемых запрещенными зонами. Такие структуры вызывают в настоящее время значительный интерес в силу их возможных разнообразных практических приложений.
Примером двумерного электромагнитного кристалла (ЭК) может служить система параллельно ориентированных тонких металлических цилиндров, обладающая полной запрещенной зоной в низкочастотной области спектра. Однако помимо наличия запрещенной зоны такие структуры интересны также тем, что обладают эффективными электрофизическими характеристиками, практически не встречающихся у обычных материалов и сред. Это позволяет отнести подобные искусственные кристаллы к категории метаматериалов.
Уже в 50-х годах прошлого века системы параллельных проводников при распространении излучения в направлении, перпендикулярном их осям, рассматривались в качестве искусственного магнитодиэлектрика, по своим свойствам аналогичного плазме, эффективная диэлектрическая проницаемость которого описывалась выражением
где ключевой параметр ωр – плазменная частота, определяющая границу запрещенной зоны. Отметим, что в металлических ЭК именно отрицательным значением диэлектрической проницаемости структуры может быть объяснено появление запрещенной зоны на низких частотах, что позволяет говорить о таких структурах, как о своеобразных ENG (ε-негативных) средах.
На частотах выше резонансной (разрешенная частотная зона) эффективная диэлектрическая проницаемость рассматриваемых структур меньше единицы, что приводит к необычному характеру отражений и преломлений волн на их границах с воздухом.
Говоря о возможности практического применения таких ЭК, очевидно, что принципиальным моментом является определение их диэлектрической проницаемости (либо показателя преломления), что в силу выражения (1) предполагает знание величины плазменной частоты. Впервые это было сделано в работе [1] на основе методов теории цепей:
Здесь d – период размещения элементов в структуре, образующих квадратную решетку, а – радиус цилиндров, с – скорость света.
В последнее десятилетие рядом исследователей были получены выражения, уточняющие диэлектрические свойства металлических ЭК. Так, в работе [2] через введение понятий эффективной плотности электронного потока и эффективной массы электронов в структуре получено следующее выражение:
В [3] в квазистатическом приближении дается оценка плазменной частоты, не имеющая ограничений на поперечные размеры элементов и выражающаяся формулой:
Все указанные выражения являются, разумеется, приближенными и позволяют определить значения эффективной диэлектрической проницаемости лишь с некоторой степенью точности, в частности, в них не учитывается конечность размеров кристалла.
Более строгими можно полагать методы, описанные в [4]. Там предлагается оценивать диэлектрические свойства ЭК на основе анализа амплитудных характеристик отраженной от него волны при ее нормальном падении на одну из его граней, а также рассматривая выполнение условий полного внутреннего отражения волн на границе кристалл – воздух. Оба этих подхода опираются на строгий численный анализ процессов в структурах методом конечных элементов.
В данной работе мы рассмотрим еще одну возможность определения эффективных диэлектрических свойств таких структур, в основе которой лежат особенности распределения поля в ЭК на частотах, соответствующих разрешенной зоне.
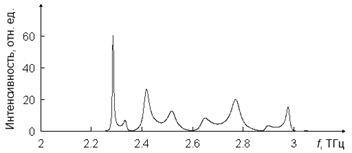
Рис. 1. Спектральное представление поля в центральной области ЭК
На рис. 1 изображено типичное спектральное распределение поля в центральной области металлического ЭК, представляющего собой квадратную решетку из 81 цилиндра, облучаемую плоской волной. Шаг решетки d = 0,5 мм, радиус элементов а = 0,05 мм, k – волновое число. Расчеты выполнялись методом самосогласованных уравнений [5] в пренебрежении потерями.
Из рисунка видно, что в разрешенной зоне полученная картина представляет собой систему резонансных пиков, число которых отличается на единицу от количества рядов в структуре в направлении прихода волны. Данная ситуация хорошо известна в теории одномерных ЭК и трактуется, как выполнение условий минимального отражения волн от структуры. В нашем случае каждому резонансу соответствует целое число полуволн, укладывающихся на длине кристалла, в чем, собственно, и проявляются дисперсионные свойства подобных структур. Первый, наиболее выраженный резонансный максимум отвечает ситуации, когда длина структуры равна половине длины волны излучения, с локализацией его в центральной области. Причем легко видеть, что длина волны в ЭК значительно превышает длину волны в окружающем пространстве, указывая на то, что эффективный показатель преломления такой структуры действительно оказывается меньше единицы.
Анализ расположения резонансных пиков на частотной оси, как и анализ их смещения при изменении геометрии ЭК дает возможность непосредственного определения эффективных диэлектрических свойств таких материалов. При этом учет конечных размеров кристалла является принципиальной составляющей метода, что, на наш взгляд, делает его максимально корректным. Здесь же отметим, что предлагаемые в [4] подходы, связанные с анализом отраженных от ЭК волн, также могут привести к погрешностям без учета резонансного характера отражений, обусловленных конечностью структуры.
На рис. 2 и 3 представлены результаты определения эффективных диэлектрических проницаемостей металлического ЭК, выполненные по предложенной методике и в соответствии с формулами (3) и (4). Выражение (2) для заданных параметров структуры приводит к значительно отличающимся результатам, которые здесь не рассматриваются.
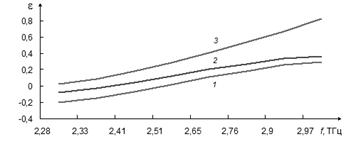
Рис. 2. Частотная зависимость эффективной диэлектрической проницаемости. Кривая 1 – формулы (1), (3), кривая 2 – формулы (1), (4), кривая 3 – описанная методика.
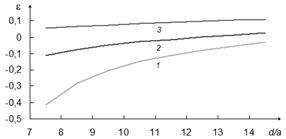
Рис. 3. Зависимость диэлектрической проницаемости ЭК от плотности заполнения структуры. Обозначения кривых – аналогично рис. 2.
Сравнение полученных зависимостей демонстрирует их существенные расхождения. Если в низкочастотной части рассматриваемого диапазона (рис. 2) это сводится к приблизительно десятипроцентным отличиям в определении плазменных частот по каждой из методик, а общий ход кривых оказывается аналогичным, то на высоких частотах поведение зависимостей существенно разнятся. Это связано с принципиальной невозможностью учета появления второй запрещенной зоны в спектре пропускания ЭК при построении аналитических выражений, а значит и диэлектрическая проницаемость, определяемая ими, будет стремиться к единице лишь на бесконечно больших частотах. Аналогичная картина наблюдается и при увеличении плотности заполнения структуры (рис. 3). С ростом отношения радиусов элементов к периоду кристалла зависимости ведут себя по-разному, в особенности первая, построенная в предположении весьма малых поперечных размеров элементов.
Предложенная методика, на наш взгляд, интересна также тем, что позволяет определять диэлектрическую проницаемость ЭК не только путем численного моделирования, но и экспериментальным образом, анализируя частотные характеристики прошедшего через такие структуры поля.
В заключение отметим, что предлагаемый метод также не лишен недостатков, поскольку не позволяет определять величину диэлектрической проницаемости в области отрицательных значений. В данном случае возможна лишь косвенная оценка этого параметра из анализа степени затухания поля в ЭК на частотах запрещенной зоны.
1. Brown J. Artificial dielectrics having refractive indices less than unity // Proc. Inst. Elect. Eng. (London). 1953. Part IV. V. 100. Monograph № 62R. P. 51-62.
2. Pendry J.B. et al. Low frequency plasmons in thin-wire structures // J. Phys. Condens. Matter. 1998. № 10. P. 4785-4799.
3. Tretyakov S.A. Analytical Modeling in Applied Electromagnetics. Artech House: Norwood, MA, 2003.
4. Schwartz B.T., Piestun R. Total external reflection from metamaterials with ultralow refractive index // J. Opt. Soc. Am. B. 2003. V. 20. № 12. P. 2448-2457.
5. Ветлужский А.Ю. Локализация излучения в двумерных случайных средах конечной протяженности // ЖЭТФ. 2009.Т. 136. № 2. С. 356 – 361.