УДК 621.396.67
ОЦЕНКА ПАРАМЕТРОВ СВЕРХШИРОКОПОЛОСНОЙ МНОГОЛУЧЕВОЙ ГИБРИДНОЙ ЛИНЗОВОЙ АНТЕННЫ
С. Е. Банков
1,
А. Г. Давыдов 2, А. А. Курушин
2
1 ИРЭ им. В.А. Котельникова РАН
2 Московское конструкторское бюро «Компас»
Статья поступила в редакцию 30 ноября 2015 г.
Аннотация. Представлены результаты исследования сверхширокополосной (СШП) многолучевой гибридной антенны (МГА) на основе линзы Люнеберга и облучателя в виде решетки, состоящей из подрешеток - кластеров. Элементарные облучатели, формирующие кластер возбуждаются многоканальным делителем мощности. На основе приближенных моделей дана оценка основных показателей качества СШП линзовой МГА: рабочего диапазона частот, коэффициента усиления (КУ), ширины главного луча диаграммы направленности (ДН), уровня пересечения лучей. Обсуждается вопрос технической реализации кластерного облучателя в виде решетки антенн Вивальди.
Ключевые слова: сверхширокополосные антенны, многолучевая антенна, гибридная антенна, линза Люнеберга, антенна Вивальди, решетка антенн Вивальди.
Abstract. Results of investigation of super wideband multi-beam hybrid antenna on the base of Luneburg lens and a clustered array are presented. Forming cluster elementary radiators are excited by a multi-channel power divider. Applying approximate models the main parameters of the antenna: gain, main beam beam-width, radiation pattern, level of beam crossing are evaluated. Application of antenna Vivaldi array as a clustered array is discussed.
Keywords: super wideband antenna, multi-beam antenna, hybrid antenna, Luneburg lens, Vivaldi antenna, Vivaldi antenna array.
Введение
Известно, что антенные системы с цифровым диаграммообразованием имеют большие перспективы в активных и пассивных РЛС [1]. Однако, их применение в пассивных РЛС наталкивается на трудности, связанные с необходимостью обеспечения достаточно широкой полосы рабочих частот. Альтернативным вариантом построения цифровой антенной решетки (ЦАР) является МГА, в которой КУ обеспечивается оптической системой, а решетка используется в качестве облучателя. Такая схема построения антенны имеет ряд преимуществ перед традиционной ЦАР при работе в СШП диапазоне.
В работе [2] рассмотрена зеркальная МГА, функционирующая по принципу постоянного коэффициента использования поверхности (КИП) зеркала в СШП диапазоне. Исследование этой системы показало, что создание облучающей решетки с постоянным в широкой полосе частот фазовым центром и постоянной шириной ДН является весьма сложной задачей. Поэтому представляет интерес исследование варианта построения МГА, работающей по принципу постоянной ширины главного луча ДН. В этом случае требование постоянства ширины ДН облучателя снимается, а выполнение условия неподвижности фазового центра относительно просто достигается при использовании в качестве облучателей апертурных антенн.
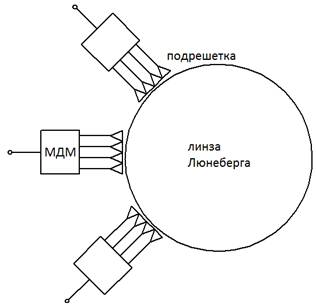
Рис. 1. Структурная схема МГА
В данной работе анализируется МГА на основе линзы Люнеберга с облучателем в виде СШП решетки антенн Вивальди. Элементарные излучатели решетки объединены в подрешетки - кластеры, которые возбуждаются при помощи многоканальных делителей мощности (МДМ) (см. рис. 1).
В работе дана оценка основных показателей качества отдельных блоков линзовой МГА и всей системы в целом. В приближении геометрической оптики и элементарной теории антенных решеток находится распределение поля в выходной апертуре линзы Люнеберга, при помощи которого в приближении физической оптики находится ДН линзы и ее вторичные параметры: коэффициент направленного действия (КНД), ширина главного луча, уровень пересечения лучей и т.д. Исследуется поведение указанных параметров в широкой полосе частот. Путем численного моделирования анализируются бесконечные решетки антенн Вивальди двух типов в режиме осевого излучения. Построена приближенная модель МДМ на основе двухпроводных полосковых линий. В приближении теории линий передачи СВЧ найден коэффициент отражения МДМ. В приближении заданных токов найдены его радиационные потери. Сравниваются разные варианты построения МДМ.
1. Характеристики излучения линзовой МГА
Анализ линзовой МГА проводился в рамках следующих приближений. Облучатель моделировался эквидистантной решеткой элементарных излучателей с прямоугольной сеткой. Его ДН находилась как произведение множителя направленности решетки на ДН излучателя, которая задавалась разными способами: ДН элемента Гюйгенса, cosq и т.д. Распределение поля в выходной апертуре линзы Люнеберга определялось по ДН облучателя в приближении геометрической оптики. При этом использовался известный закон отображения линзы Люнеберга [3]. По найденному амплитудно - фазовому распределению в приближении заданных источников (приближение Кирхгофа) находилось поле излучения линзы Люнеберга. При этом определялась ДН, КНД, ширина главного луча ДН, уровень пересечения соседних лучей. Поле излучения находилось в скалярном приближении без учета поляризационных эффектов.
Исходными параметрами для анализа характеристик излучения в модели описанной выше служат угловое расстояние между соседними лучами МГА dq и радиус линзы Люнеберга R, размерность кластера N. Исходя из них находится линейный размер облучающего кластера d=Rdq. Отметим, что параметр d определяется из условия отсутствия зазоров между соседними кластерами. Период P задается размером кластера P=d/N. Таким образом, определяются все параметры структуры.
Рассмотрим некоторые результаты расчетов. На первом этапе исследовался кластер с равномерным амплитудным распределением в апертуре.
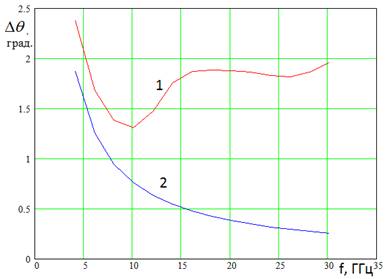
Рис. 2. Частотная зависимость ширины ДН линзовой МГА
На рис. 2 показана частотная зависимость ширины ДН Dq по уровню - 3 дБ. Кривые 1,2 получены для dq=20, N=4, R=1000 мм, Р=8.7 мм. Кривая 1 соответствует МГА, а кривая 2 идеальной круглой апертурной антенне радиуса R. Видно, что ширина ДН в диапазоне частот 1:6 меняется в пределах 1.5-20. При этом на высоких частотах она существенно больше ширины ДН идеальной антенны, что является следствием принципа работы МГА с постоянной шириной луча. Для его реализации на высоких частотах линза облучается частично, что находит отражение в расширении ДН МГА по отношению к идеальной антенне.
На рис. 3 представлена частотная зависимость КНД линзовой МГА. Видно, что КНД достаточно слабо меняется в рассматриваемом диапазоне. На низких частотах наблюдается тенденция к снижению КНД. Рабочий диапазон антенны определяется следующими факторами. Нижняя частота диапазона задается условием: NP=l/2, где l - длина волны в свободном пространстве. Ниже этой частоты ДН кластера перестает меняться при изменении частоты и КНД антенны падает. Верхняя частота рабочего диапазона определяется появлением в ДН облучающей решетки побочных дифракционных максимумов.

Рис. 3. Частотная зависимость КНД
Они возникают, когда период решетки равен длине волны l. В этом случае диапазон рабочих частот (отношение верхней частоты к нижней) равен 2N. Однако, на практике нормальная работа решетки оказывается нарушенной на существенно более низких частотах вследствие резонансных эффектов, обусловленных возбуждением в ней высших типов волн. Чаще всего они возникают, когда P>l/2. Исключение данного диапазона уменьшает полосу рабочих частот в два раза. Таким образом, окончательный ответ о верхней границе диапазона МГА может дать только электродинамическое исследование решетки.
На рис. 4 показана частотная зависимость уровня пересечения лучей (УПЛ), создаваемых соседними кластерами. Видно, что лучи пересекаются на довольно низком уровне (в среднем - 6 дБ) за исключением области низких частот, в которой УПЛ повышается.
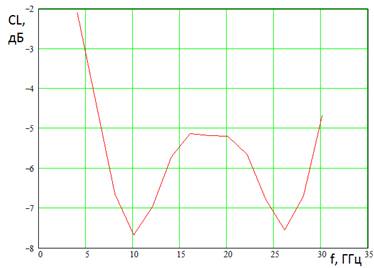
Рис. 4. УПЛ линзовой МГА
На относительно низких частотах (см. рис. 5) главный луч ДН имеет обычную форму. На высоких частотах происходит ее изменение. Она приближается к прямоугольной (см. рис. 6). Данное явление является следствием неполного облучения поверхности линзы.
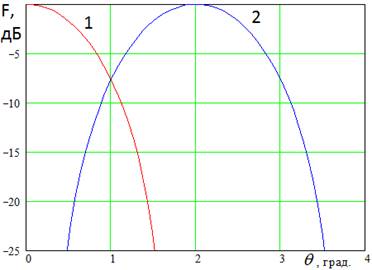
Рис. 5. ДН на частоте 8 ГГц
Если учесть, что ДН связана с распределением создающих ее источников через преобразование Фурье, то нетрудно показать, что ДН линзы на высоких частотах должна повторять распределение поля в кластере, которое описывается прямоугольной функцией.

Рис. 6. ДН на частоте 21 ГГц
На следующем этапе исследовалось влияние амплитудного распределения поля в кластере на параметры МГА. Результаты исследования показаны на рис. 7 – 9. Расчеты проводились для распределения типа «косинус на пьедестале» с уменьшением на краю на 6 дБ. Видно, что изменение распределение в кластере привело к существенному уменьшению ширины ДН (см. рис. 7), которое увеличило КНД (рис. 8) и уменьшило УПЛ (рис. 9). Теперь лучи пересекаются на уровне – 13 дБ. Форма их улучшилась по сравнению с рис. 6, однако мы можем говорить о появлении «слепых» зон между лучами, что во многих случаях неприемлемо.
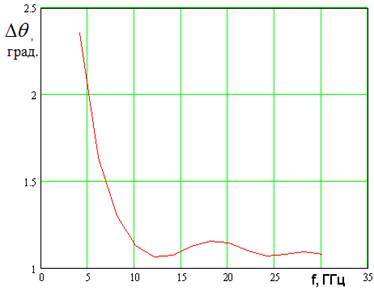
Рис. 7. Ширина ДН МГА
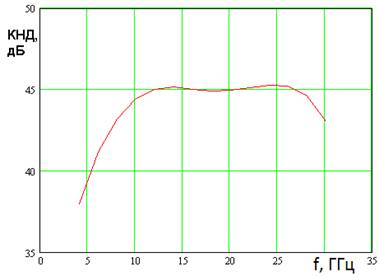
Рис. 8. КНД МГА
Противоречие между формой лучей линзовой МГА, УПЛ и КНД невозможно устранить при использовании изолированных кластерных облучателей, поскольку высокий уровень пересечения лучей требует применения пересекающихся кластеров [4]. Однако их создание для работы в СШП весьма затруднительно.
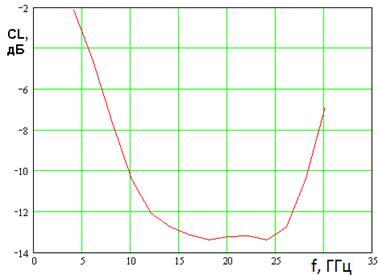
Рис. 9. УПЛ линзовой МГА
2. Исследование решеток антенн Вивальди
Решетки антенн Вивальди исследовались в приближении бесконечной решетки при помощи стандартных программ электродинамического моделирования. При этом использовалась модель в виде канала Флоке, который представляет собой СВЧ четырехполюсник. Один его вход – это физический вход антенны Вивальди, а второй вход – порт Флоке является виртуальным портом, который моделирует плоскую волну свободного пространства. Расчеты матрицы рассеяния канала Флоке проводились в режиме излучения по нормали. Также использовались данные из литературы. Рассматривались два типа двухполяризационных антенн Вивальди: с выходом на двухпроводной линии и с переходом на полосковую линию (см. рис. 10 а,б).
Проведенные расчеты, а также анализ известных литературных данных позволяет сделать ряд выводов. В диапазоне длин волн меньших 2Р (частота больше 2с/Р, с – скорость света в вакууме) использование решеток антенн Вивальди всех типов затруднительно из-за возбуждения высших типов волн и сопутствующих им резонансов. В этом можно убедиться, рассматривая график на рис. 11. На рис. 11 показана частотная зависимость коэффициента передачи канала Флоке для идеализированной решетки антенн Вивальди, имеющих выходы в виде щелевых линий передачи. Такая структура позволяет исключить влияние на параметры решетки узла возбуждения щелевой линии. Кривая на рис. 11 получена для периода Р=15 мм и длины антенны Вивальди L=90 мм.

Рис. 10. Антенны Вивальди
Видно, что при частотах ![]() ГГц, то есть при длинах волн короче 2Р
в частотной зависимости коэффициента передачи наблюдаются резкие провалы,
связанные с возбуждением в решетке антенн Вивальди паразитных типов волн.
Отсюда можно сделать важный вывод о том, что верхняя граница рабочего диапазона
решетки определяется условием
ГГц, то есть при длинах волн короче 2Р
в частотной зависимости коэффициента передачи наблюдаются резкие провалы,
связанные с возбуждением в решетке антенн Вивальди паразитных типов волн.
Отсюда можно сделать важный вывод о том, что верхняя граница рабочего диапазона
решетки определяется условием ![]() , а не условием
, а не условием ![]() , следующим из элементарной теории
антенных решеток.
, следующим из элементарной теории
антенных решеток.

Рис. 11. Частотная зависимость коэффициента передачи
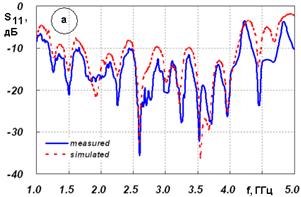
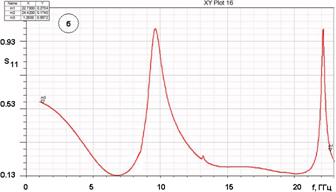
Рис. 12. АЧХ антенн на рис. 10 а,б
Нижняя граничная частот решетки антенн Вивальди с выходом на полосковой линии передачи определяется длиной антенны и характеристиками перехода щелевая линия – полосковая линия. Поскольку длина антенны может быть легко увеличена, то основным фактором становится переход. В структурах аналогичных изображенной на рис. 10 а максимальное отношение верхней частоты к нижней можно оценить как 4:1. Типичный пример частотной зависимости коэффициента отражения приведен на рис. 12 а. Длина антенны 120, а период решетки 60 мм. Рисунок взят из работы [5]. Видно, что модуль S11 ниже – 10 дБ на частотах от 1.2 до 4.2 ГГц.
Лучшие перспективы с точки зрения расширения полосы частот должна иметь решетка антенн Вивальди с выходом на двухпроводной линии (рис. 10 б), которая не содержит резких нерегулярностей. В первом приближении ее функционирование можно рассматривать как работу плавного трансформатора сопротивления. Однако электродинамические расчеты показали недостаточность простой модели, поскольку были обнаружены резонансные явления на частотах существенно меньших 2с/Р. Пример частотной зависимости коэффициента отражения для структуры на рис. 10 б показан на рис. 12 б. Кривая получена для антенны длиной 60 и периодом 10 мм.
Видно, что на частоте около 8 ГГц наблюдается выброс модуля коэффициента отражения. Появление резонансов на сравнительно низких частотах объясняется тем, что в отличие от структуры на рис. 10 а период решетки на рис. 10 б является многопроводной, а, следовательно, многомодовой структурой, в которой распространяются две Т – волны, не имеющие частот отсечки. Одна из этих волн плавно трансформируется в волну щелевой линии (область 2 на рис. 10 б) и затем излучается в свободное пространство. Другая волна остается запертой в области 1 и формирует достаточно добротное колебание.
Для борьбы с указанными резонансами была предложена модифицированная структура изображенная на рис. 13. Она также имеет выход на двухпроводной линии, но форма проводников отличается от показанной на рис. 10 б.
На рис. 14 показана частотная характеристика коэффициента отражения решетки с периодом и длиной, приведенными выше. Видно, что в решетке из модифицированных элементов можно получить отношение верхней частоты к нижней близкое к 8:1.

Рис. 13. Модифицированная антенна Вивальди
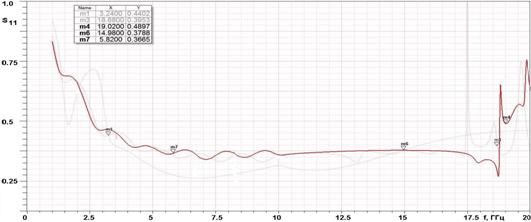
Рис. 14. Частотная зависимость коэффициента отражения решетки модифицированных антенн Вивальди
В целом следует отметить, что детальная оценка параметров облучателей на основе решеток антенн Вивальди требует более глубокого исследования, в частности, ее поведения при углах отличных от нормального. Особенно это актуально для оценки характеристик в нижней части диапазона, в которой облучатель имеет широкую ДН.
3. Многоканальные делители мощности
Рассматривалась элементная база МДМ (см. рис. 15 а-г). В нее входят элементарные делители мощности (ЭДМ) на два канала (рис. 15 а-г), переход с несимметричной полосковой линии на симметричную двухпроводную линию (рис. 15 д) и скрутка двухпроводной линии (рис. 15 е). Среди ЭДМ можно выделить Т - образные делители в Е и Н плоскостях (см. рис. 15 а,б) и плавные делители в указанных областях. Анализ ЭДМ и скрутки проводился приближенным методом без учета диэлектрической подложки. Матрица рассеяния ЭДМ определялась в рамках теории линий передачи.
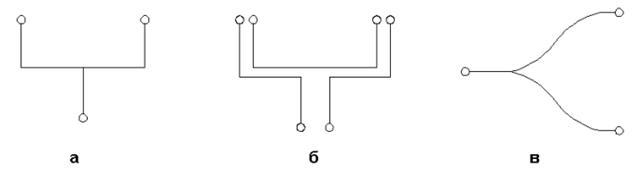
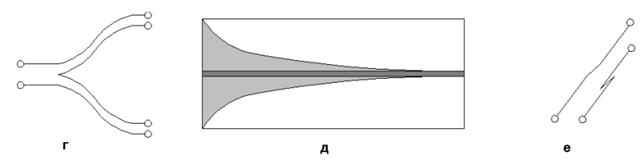
Рис. 15. Элементная база МДМ
Потери на излучение оценивались в приближении заданных токов. Проводники линий передачи, образующих ЭДМ заменялись нитями токов, расположенными в свободном пространстве. При этом предполагали, что ЭДМ идеально согласован. При записи токов учитывалось условие их непрерывности. По заданным токам определялось поле их излучения в дальней зоне и вычислялась мощность потерь излучения. Суммарные потери вычислялись как сумма потерь на отражение и излучение. Тепловые потери в линиях передачи рассчитывались при помощи системы Microwave Office.
В работе рассматривались разные схемы
построения МДМ. МДМ, возбуждающий решетку имеет двумерную структуру, поскольку
его выходы распределены на плоскости. Поскольку облучающая линзу решетка должна
работать с волнами двух ортогональных поляризаций, то для возбуждения кластера
размерностью ![]() необходимо использовать два двумерных МДМ
такой же размерности. Совмещение двух МДМ в ограниченном пространстве представляет
довольно сложную задачу. Один из вариантов ее решения состоит в применении МДМ,
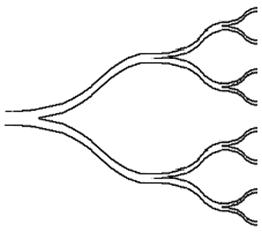
состоящих из линейных, то есть одномерных МДМ, показанных на рис. 16 а,б.
необходимо использовать два двумерных МДМ
такой же размерности. Совмещение двух МДМ в ограниченном пространстве представляет
довольно сложную задачу. Один из вариантов ее решения состоит в применении МДМ,
состоящих из линейных, то есть одномерных МДМ, показанных на рис. 16 а,б.
а б
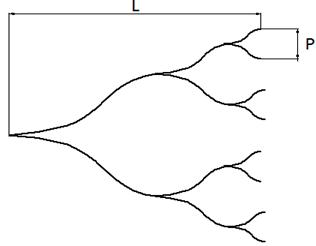
Рис. 16. Линейные МДМ на плавных ЭДМ
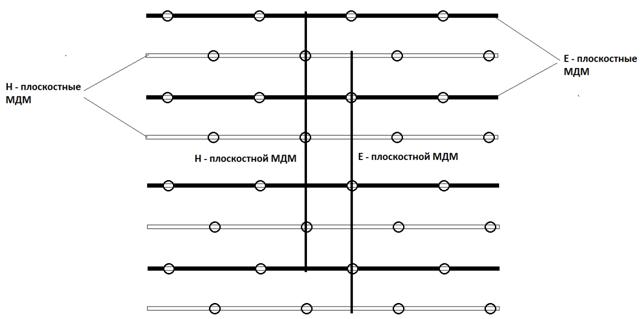
Рис. 17. Два совмещенных двумерных МДМ
Линейные делители могут осуществлять деление в Е и Н - плоскостях. МДМ изображенный на рис. 16 а делит мощность в Е - плоскости, а делитель на рис. 16 б в Н - плоскости.
При помощи Е и Н - плоскостных одномерных МДМ может быть решена задача создания двумерного двухполяризационного МДМ. Пример такого решения показан на рис. 17. За счет комбинации делителей разного типа удается разместить два делителя в одном пространстве.
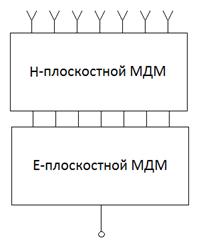
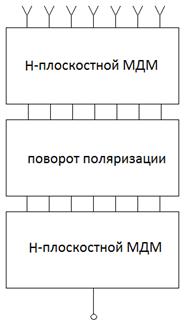
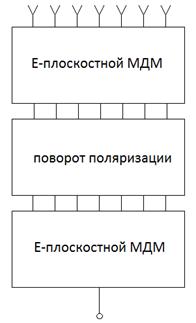
Схема изображенная на рис. 17 является одной из возможных схем построения двумерных МДМ. В работе также анализировались другие варианты построения делителей. Их схемы показаны на рис. 18 а-г. Среди них выделим вариант 1: Н-плоскостной МДМ, Е-плоскостной МДМ (см. рис. 18 а), вариант 2: Н-плоскостной МДМ, поворот плоскости поляризации (скрутка, см. рис. 18 б), Н-плоскостной МДМ, вариант 3: Е-плоскостной МДМ, скрутка, Е-плоскостной МДМ (см. рис. 18 в).
а б в
г
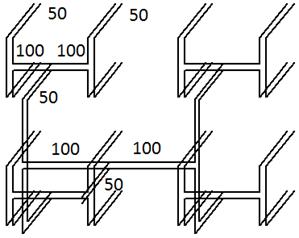
Рис. 18. Схемы построения двумерных МДМ
Большой интерес представляет схема, изображенная на рис. 18 г. В отличие от схем на рис. 18 а-в в ней нет каскадного соединения линейных МДМ. Кроме того она построена на Т - образных ЭДМ в разных плоскостях и поворотах линий передачи. С конструктивной точки зрения такая схема весьма привлекательна, так как комбинация Н и Е-плоскостных ЭДМ позволяет создавать делители без трансформаторов сопротивления. Они содержат только линии передачи с сопротивлениями двух номиналов: 50 и 100 Ом. Такие МДМ не имеют ограничений на низких частотах.
Для оценки параметров МДМ
важным фактором является расчет тепловых потерь, которые определяются
затуханием волны в образующих их линиях передачи. Как отмечалось выше для
оценки этого параметры мы использовали систему Microwave Office. В качестве линии передачи рассматривалась
двухпроводная полосковая линия на подложке с проницаемостью ![]() ,
, ![]() и
толщиной 1 мм. На рис. 19 показана зависимость ее постоянной затухания от
частоты.
и
толщиной 1 мм. На рис. 19 показана зависимость ее постоянной затухания от
частоты.
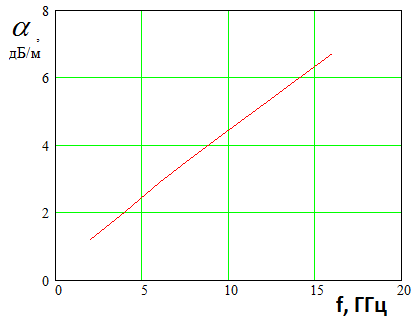
Рис. 19. Частотная зависимость затухания в микрополосковой линии
К сожалению, применение МДМ на Т - образных ЭДМ на относительно высоких частотах ограничено потерями на излучение. На рис. 20 показана зависимость суммарных потерь в МДМ размерностью 8х8 каналов. Кривая 1 соответствует МДМ на Т - образных ЭДМ, а кривая 2 МДМ по схеме линейный делитель в Е - плоскости и линейный делитель в Н - плоскости. Видно, что верхняя граница частотного диапазона МДМ лежит в пределах 6-7 ГГц. На более высоких частотах делитель на элементарных плавных Y - делителях имеет существенное преимущество.
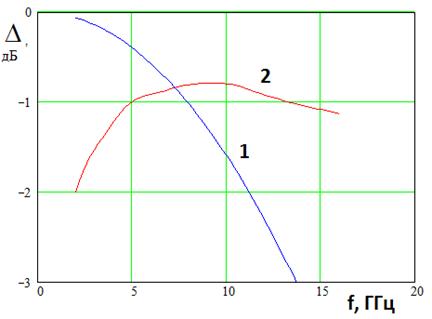
Рис. 20. Частотная зависимость потерь в МДМ
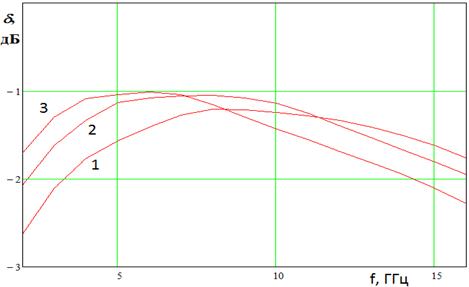
Рис. 21. Частотная зависимость суммарных потерь в МДМ на 64 канала
Частотная зависимость потерь в плавных МДМ имеет экстремум.
На низких частотах основным источником потерь в МДМ служат потери на отражение.
На высоких частотах доминируют тепловые и радиационные потери. На рис. 21
приведена частотная зависимость потерь МДМ на 64 (8х8) канала по варианту
линейный делитель в Е - плоскости и линейный делитель в Н - плоскости. Кривые
1-3 получены для Р=9.4, L=96, 149.6, 209.7 мм, где ![]() - полная длина МДМ.
Тепловое затухание рассчитывалось для двухпроводной полосковой линии на
подложке с проницаемостью равной 2 и толщиной 1 мм. Видно, что существует оптимальное значение
- полная длина МДМ.
Тепловое затухание рассчитывалось для двухпроводной полосковой линии на
подложке с проницаемостью равной 2 и толщиной 1 мм. Видно, что существует оптимальное значение ![]() , обеспечивающее
близкие потери на верхней и нижней границах частотного диапазона.
, обеспечивающее
близкие потери на верхней и нижней границах частотного диапазона.
Отметим, что суммарные потери во всех вариантах МДМ на основе плавных ЭДМ имеют близкие значения. Поэтому численные данные для других схем МДМ мы не приводим.
Заключение
Представленные в работе результаты соответствуют этапу эскизного проектирования СШП МГА на основе линзы Люнеберга. Они позволяют приближенно оценить ее показатели качества и выбрать наиболее перспективные варианты построения отдельных блоков. Более точная оценка технических характеристик МГА будет получена на этапе технического проектирования путем электродинамического моделирования и экспериментальных исследований.
Литература
1. Ратынский М.В. Адаптация и сверхразрешение в антенных решетках. - М.: Радио и связь, 2003.
2. Мануилов Б.Д., Башлы П.Н., Мануилов М.Б., Безуглов Ю.Д., Климухин Д.В. Многофункциональные антенные решетки с комплексным управлением. Ростов на Дону: Изд-во РВИ РВ. 2010.
3. Корнблит С. СВЧ оптика. Оптические принципы в приложении к конструированию СВЧ антенн. М.: Связь. 1980.
4. Скобелев С.П.Фазированные антенные решетки с секторными диаграммами направленности. М.: Физматлит. 2010.
5. Yang Y., Wang Y., and Fathy A.E. Design of a compact Vivaldi antenna arrays for UWB SEE through wall applications // PIERS 82, p.p. 401–418, 2008.