 |
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 7, 2002 |
 |
МЕТОД ФОРМИРОВАНИЯ РЕАЛИЗУЕМОЙ ЗАДАННОЙ ДИАГРАММЫ НАПРАВЛЕННОСТИ В ЗАДАЧАХ СИНТЕЗА АНТЕННЫХ РЕШЕТОК
Мищенко С. Е. , e-mail: mihome@jeo.ru
Ростовский военный институт ракетных войск.
Получена 15 июля 2002 г.
В работе предложен итерационный метод формирования реализуемой диаграммы направленности антенной решетки точечных изотропных излучателей. Данный метод позволяет снизить произвол при выборе заданной диаграммы направленности в задачах синтеза антенных решеток. В работе приведен алгоритм, реализующий предлагаемый метод и приводящий при определенных начальных параметрах итерационного процесса к чебышевской диаграмме направленности. Приведены примеры синтеза линейной антенной решетки по сформированной заданной диаграмме направленности.
Задачи синтеза антенных
решеток (АР) очень часто рассматривают как задачу о приближении двух функций 
и 
[1,2]. В таких задачах функция описывает желаемую
характеристику направленности антенны, а функция — реализуемую диаграмму направленности
(ДН). Функция должна
удовлетворять целому ряду прагматических требований: к положению максимума ДН,
ширине луча по уровню половинной мощности 
, максимальному уровню боковых лепестков 
. Кроме того, могут
предъявляться требования к положению «нулей» ДН антенны. Такому набору
требований может удовлетворять бесконечное количество функций. Поэтому при
выборе заданной функции существует определенный произвол, который может
сказаться на решении задачи синтеза. В монографии [1] сформулированы условия
существования точного решения задачи аппроксимационного синтеза линейной АР,
однако, эти условия не позволяют на этапе постановки задачи обоснованным
образом выбирать функцию , описывающую желаемую ДН.
В работе предлагается
итерационный метод выбора заданной ДН, описываемой четной функцией , которая принадлежит
множеству реализуемых диаграмм линейной эквидистантной АР точечных излучателей.
И приведены примеры численного решения задачи синтеза, полученные с
использованием аналитических методов.
В соответствии с
[1] ДН
линейной эквидистантной АР с симметричными амплитудным и фазовым
распределениями, состоящая из четного числа 
точечных изотропных излучателей, может
быть представлена в виде
, (1)где
;
— комплексная амплитуда возбуждения 
-го излучателя; 
— шаг между
излучателями; 
—
волновое число; 
—
некоторый параметр.
В случае нечетного 
числа излучателей ДН
антенны может определяется выражением
. (2)Формируемые на основе
выражений (1) и (2) функции , по-видимому, обладают свойством симметрии
относительно направления 
и могут быть как комплексными, так и
действительными.
С использованием
выражений (1) и (2) задача синтеза АР по заданной ДН в рассматриваемом случае
может быть сформулирована как задача о поиске комплексных коэффициентов полинома , обеспечивающего
наилучшее приближение к функции в смысле диаграммного функционала 
. Очевидно, что
наилучшее решение будет в том случае, когда функции и полностью совпадут. При этом 
. Следует заметить, что
если такое решение существует, то выбор диаграммного функционала не оказывает
влияния на коэффициенты 
.
Сначала рассмотрим задачу синтеза АР, ДН которой описывается выражением (1), т.е. антенна содержит четное количество излучателей.
С использованием известных итерационных формул для многочленов Чебышева [2]
;
,
выражение (1) может быть представлено в виде
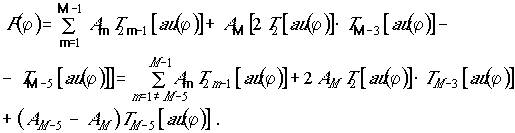
Продолжая подобные преобразования, для АР с ДН вида (1) получим следующее выражение
(3)Здесь символ «~» над
коэффициентами обозначает,
что в выражении (3) выполнена операция приведения подобных слагаемых.
Выражение (3) может быть также представлено в виде итерационного алгоритма
, 
, (4)где 
— постоянный коэффициент; 
— шаг итерационного
процесса.
Аналогичный итерационный процесс может быть предложен и для полинома (2). В этом случае итерационный процесс для формирования реализуемой ДН описывается выражением вида
, (5)где 
и 
— постоянные коэффициенты.
Выражения (4) и (5)
являются общими и позволяют получить реализуемую функцию 
для любого произвольного набора
коэффициентов и
. Однако
количество коэффициентов и будет соизмеримо с количеством слагаемых в
полиномах (1) и (2), что делает задачу формирования функции соизмеримой по сложности с
задачей о приближении функций. Поэтому необходимо разработать такой алгоритм
выбора коэффициентов и
, который в
определенных случаях будет приводить к типичным заданным функциям, часто
используемым при решении подобных аппроксимационных задач. При этом количество
начальных параметров в выражениях (4) и (5) может быть снижено.
Данная идея была
использована при построении итерационного алгоритма, который приводит при
некоторых начальных условиях к формированию функций вида 
и 
для четного и нечетного числа излучателей
АР соответственно.
Сначала выразим в виде (4) и (5) несколько многочленов Чебышева с младшими порядковыми номерами:
;
;
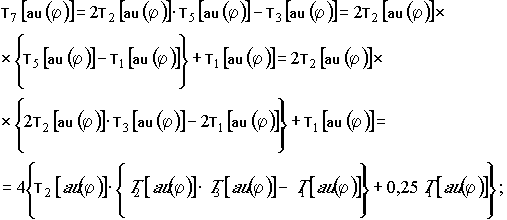Таблица 1. Коэффициенты итерационного процесса
2M |
Номер шага итерационного процесса n+1, n=0,1,2,… |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
6 |
-1/2 |
¾ |
¾ |
¾ |
¾ |
¾ |
¾ |
¾ |
¾ |
¾ |
|
8 |
-2/2 |
1/4 |
¾ |
¾ |
¾ |
¾ |
¾ |
¾ |
¾ |
¾ |
|
10 |
-3/2 |
2/4 |
1/8 |
¾ |
¾ |
¾ |
¾ |
¾ |
¾ |
¾ |
|
12 |
-4/2 |
3/4 |
3/8 |
-1/16 |
¾ |
¾ |
¾ |
¾ |
¾ |
¾ |
|
14 |
-5/2 |
4/4 |
6/8 |
-3/16 |
-1/32 |
¾ |
¾ |
¾ |
¾ |
¾ |
|
16 |
-6/2 |
5/4 |
10/8 |
-6/16 |
-4/32 |
1/64 |
¾ |
¾ |
¾ |
¾ |
|
18 |
-7/2 |
6/4 |
15/8 |
-10/16 |
-10/32 |
4/64 |
1/128 |
¾ |
¾ |
¾ |
|
20 |
-8/2 |
7/4 |
21/8 |
-15/16 |
-20/32 |
10/64 |
8/128 |
-1/256 |
¾ |
¾ |
|
22 |
-9/2 |
8/4 |
28/8 |
-21/16 |
-35/32 |
20/64 |
15/128 |
-5/256 |
-6/512 |
¾ |
|
24 |
-10/2 |
9/4 |
36/8 |
-28/16 |
-56/32 |
35/64 |
35/128 |
-15/256 |
-6/512 |
1/1024 |
Продолжая данный ряд для
полинома (1), запишем получаемые коэффициенты в
таблицу 1, в которой
представлены коэффициенты , соответствующие нечетным многочленам Чебышева.
При этом в качестве начальной функции 
выбирается 
. Каждая строка таблицы соответствует
определенному номеру 
формируемого
многочлена Чебышева, а также числу 
элементов АР, которая реализует ДН, описываемую
соответствующим многочленом Чебышева. Каждый ряд значений коэффициентов соответствует номеру
шага итерационного процесса (4). Прочерки в ячейках таблицы обозначают, что
многочлен Чебышева был сформирован на предыдущих шагах итерационного процесса.
Проведенные исследования
показали, что коэффициенты таблицы 1 могут быть использованы и в случае
формирования полинома (2). При этом на нечетных шагах процесса коэффициенты 
, а коэффициенты выбираются из
таблицы
1. На четных шагах, наоборот, 
, а коэффициенты 
выбираются из соответствующих
ячеек таблицы 1.
Из анализа коэффициентов таблицы 1 видно, что можно представить в
виде произведения 
.
Как видно из таблицы 1, 
.
Для вычисления функции 
на основании
таблицы 1
может быть предложен следующий численный алгоритм.
Пусть необходимо
вычислить нечетный многочлен Чебышева 
, для чего потребуется 
коэффициентов из таблицы 1.
Тогда необходимо определить значения функции , соответствующие 
-ой строке данных в
таблице 1.
Для этого введем вспомогательную квадратную матрицу 
. При этом набор значений функции
составляют
элементы -ой
строки матрицы 
.
Для заполнения матрицы может
быть использован следующий алгоритм.
1. Заполняются два первых столбца
матрицы . При
этом 
, 
.
2. Заполняются диагональные элементы
матрицы . При
этом 
.
3. Заполняется сверху вниз первый
незаполненный нечетный столбец матрицы по формуле 
(
).
4. Заполняется первый незаполненный
четный столбец матрицы 
по правилу
; 
.
5. Шаги 3 и 4 алгоритма повторяются до
тех пор пока не заполнятся все свободные столбцы матрицы .
6. Вычисляется знак элементов в столбцах
матрицы с
помощью формулы
.
Здесь 
обозначает операцию округления
до ближайшего целого.
Для найденных значений
функций 
и набор коэффициентов в
выражении (3), определяется выражением 
. При 
рекуррентная формула (4) приводит к
формированию нечетного многочлена Чебышева на шаге. Легко убедиться, что при
действительных 
получаемая
с помощью (4) функция представляет собой суперпозицию нечетных многочленов
Чебышева с номерами, не превышающими 
.
В случае, когда
формируется комплексная функция, между реальной и мнимой частями реализуемой ДН
АР должна существовать определенная взаимосвязь. Поэтому нельзя применить
предлагаемый подход для независимого формирования реальной и мнимой части
функции .
Однако в случае, если для реальной и мнимой части выбирается одна и та же
функция 
, то
необходимая взаимосвязь между реальной и мнимой частями реализуемой ДН АР
сохраняется. Это обусловлено тем, что приведение подобных в выражении (3) в
случае комплексных коэффициентов 
может осуществляться для реальной и мнимой
части независимо. Таким образом, для формирования реализуемой комплексной ДН необходимо
выбрать два коэффициента 
и одну общую функцию , например, определенную с
использованием предложенного выше алгоритма.
Данный алгоритм может
быть использован и для формирования коэффициентов и (5) четных многочленов Чебышева. При этом
в таблице 1 количество излучателей АР в каждой ячейке необходимо будет
увеличить на единицу, а в качестве функции выбирать 
.
Таким образом,
предлагаемый алгоритм позволяет формировать реализуемые линейной АР точечных
изотропных излучателей комплексные функции вида и , представимые выражениями (1) и (2).
Аналогичные рассуждения позволяют получить и другие алгоритмы формирования ДН. В частности, был разработан алгоритм, приводящий при определенных начальных условиях к формированию ДН АР с равномерным синфазным возбуждением [3]. Данный алгоритм не приводится для сокращения объема статьи. Между тем для его получения можно воспользоваться рассуждениями, приведенными при получении первого алгоритма.
При проведении численных
исследований была рассмотрена задача формирования заданной четной функции , принадлежащей к
множеству реализуемых ДН антенной решетки, состоящей из 
точечных изотропных излучателей.
В качестве требований к функции были заданы: ширина луча по уровню
половинной мощности 
и
максимальный уровень боковых лепестков в децибелах 
.
Для анализа возможных
множеств начальных условий итерационного процесса были построены функции с использованием
начальных условий: ,
, 
.
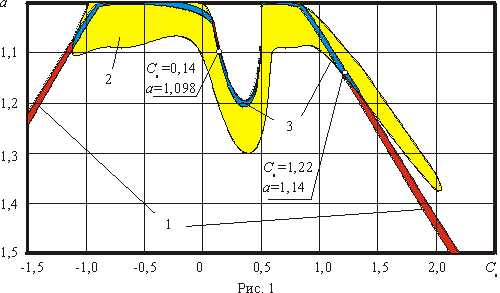
На
рис. 1 приведены
результаты анализа множества начальных условий, приводящих к функциям,
обладающими заданными свойствами. Штрихованные области 1 и 2 на данном рисунке
соответствуют начальным параметрам 
и обеспечивающим заданную ширину луча и
уровень боковых лепестков соответственно. Область 3, закрашенная черным цветом
соответствует значениям начальных параметров, которые обеспечивают
одновременное выполнение требований к и .
Выбор любых начальных условий из области 3 на рис.1 позволяет получить диаграмму направленности линейной эквидистантной АР, которая будет удовлетворять сформулированным требованиям. Однако каждая из получаемых функций будет приводить и к уникальному амплитудно-фазовому распределению в раскрыве антенны.
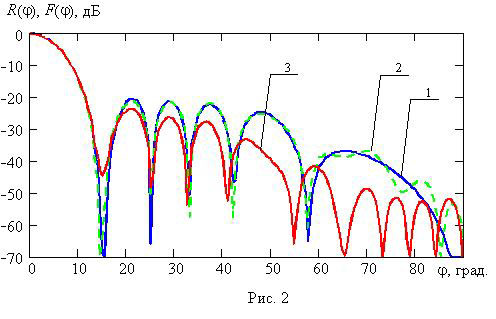
На
рис. 2 приведены
результаты формирования ДН при начальных параметрах 
и 
(кривая 1).
Известно, что в случае
рассматриваемой в работе линейной системы точечных излучателей, распределение
поля вдоль решетки может быть вычислено с помощью ряда Фурье, количество
комплексных коэффициентов которого будет совпадать с числом излучателей
[1].
Поэтому, если количество излучателей 
фиксировано и в качестве требуемой ДН
задана реализуемая функция, то для вычисления комплексных амплитуд возбуждения
излучателей решетки потребуется вычислить 
младших коэффициентов Фурье.
Для представленной на
рис. 2 функции были
найдены 32 первых комплексных коэффициента Фурье. Выполнение обратного
преобразования позволяет получить функцию , которая обозначена на рис. 2 кривой 1.
Как видно, функции и
совпадают
между собой с графической точностью в области главного лепестка. Заметные (но
несущественные) отличия появляются только для последних боковых лепестков.
Наличие расхождений между двумя функциями в области боковых лепестков
обусловлено ошибками округления, которые имели место при формировании функции .
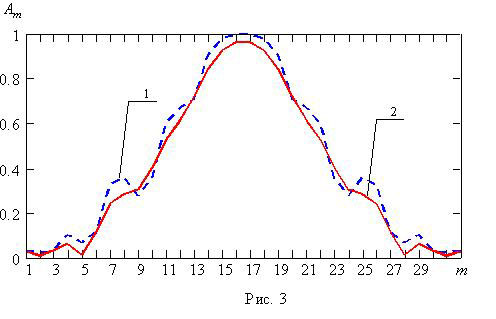
На
рис. 3 представлено
амплитудное распределение (кривая 1), необходимое для формирования заданной ДН,
найденное с использованием разложения функции 
в ряд Фурье. Как видно, получаемое
распределение является сильно изрезанным, поэтому непосредственное его
использование на практике не является целесообразным. В связи с этим для
получения более плавного распределения была проведена операция сглаживания. Для
этого использовались методы скользящего среднего (усреднение происходило по
двум соседним значениям) и метод экспоненциального сглаживания (фактор
затухания был выбран равным 0,4). Полученное сглаженное амплитудное
распределение представлено на рис. 3 кривой 2. С использованием сглаженного
амплитудного распределения была сформирована ДН АР точечных излучателей,
которая приведена на рис. 2 (кривая 3).
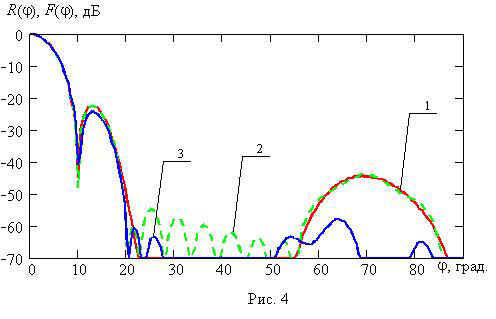
Аналогичные результаты
для начальных параметров итерационного процесса 
и 
представлены на рис. 4 и
рис. 5.
Обозначения на данных рисунках аналогичны тем, которые были введены на
рис. 2 и
рис. 3 соответственно.
Представленные результаты показывают, что предложенный итерационный метод выбора заданной ДН может быть использован для аналитического решения задачи амплитудно-фазового синтеза АР точечных излучателей. В случае АР с более реальными излучателями можно ожидать, что использование разработанного метода позволит выбирать в достаточной степени близкую к классу реализуемых заданную ДН. Это позволит избежать некорректной постановки задачи синтеза и сократить объем вычислительных затрат для ее решения.
В данной работе на форму
функции накладывались
только ограничения, связанные с уровнем боковых лепестков и шириной главного
луча по уровню половинной мощности. Однако предложенный метод позволяет
произвольным образом формулировать подобные требования. К примеру, можно
построить рисунок, аналогичный рис. 1, накладывая требования на положения нулей ДН. Отсутствие общих областей начальных параметров, приводящих к формированию
заданной ДН, будет говорить о нереализуемости сформулированных требований.
Поэтому предложенный метод может быть использован для оценки потенциальных
возможностей АР.
Таким образом,
итерационный метод и предлагаемый алгоритм формирования функций позволяет уменьшить
произвол выбора заданных функций в задачах приближения функций полиномами вида (1) и
(2). Применение предлагаемого метода в задачах аппроксимационного синтеза
антенн позволяет оценивать реализуемость предъявляемых требований на этапе
постановки задачи, а также использовать наиболее простые в вычислительном
отношении методы в ходе решения задач синтеза АР.
Работа выполнена при финансовой поддержке РФФИ (коды проектов № 01-01-00030 и № 02-01-06362).
СПИСОК ЛИТЕРАТУРЫ
1. Зелкин Е.Г., Соколов В.Г. Методы синтеза антенн: Фазированные антенные решетки и антенны с непрерывным раскрывом. — М.: Сов. радио, 1980.
2. Справочник по специальным функциям с формулами, графиками и математическими таблицами // Под ред. М. Абрамовица и И. Стигана. — М.: Наука, 1979.
3. Мищенко С.Е. Итерационный метод формирования реализуемых функций в задачах аппроксимации // Электронный журнал «Исследовано в России», 2002, № 30, С.317-326.
 |
 |