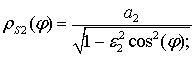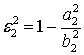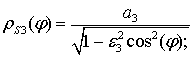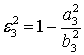О рассеянии поля цилиндрической волны идеально проводящим эллиптическим цилиндром, окруженным слоем метаматериала.

"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" №7, 2007

УДК 538.566.2;621.371

О рассеянии поля цилиндрической волны идеально проводящим

эллиптическим цилиндром, окруженным слоем метаматериала

А.П. Анютин
Российский Новый Университет, Москва

Получена 30 июля 2007 г.

   Приводятся результаты строгих расчетов диаграммы рассеяния идеально проводящего эллиптического цилиндра, покрытого слоем метаматериала конечной толщины. Исследовано влияние геометрических размеров, показателя преломления и потерь среды, а так же положения источника цилиндрической волны на диаграмму рассеяния. Показано уменьшение уровня обратного рассеяния .

ВВЕДЕНИЕ

        В последнее время наблюдается значительный рост числа публикаций, в которых рассматриваются эффекты, возникающие при взаимодействии электромагнитных волн со средой, относительная диэлектрическая и магнитная проницаемости которой одновременно являются отрицательными величинами () . Такую среду принято называть средой с отрицательной рефракцией (метаматериалом, средой Веселаго), поскольку впервые задача распространения электромагнитных волн в среде с была теоретически рассмотрена В.Веселаго еще в 1968 г. [1]. В этой работе он исследовал прохождение плоских и цилиндрических гармонических волн через плоский слой среды с конечной толщины   и показал, что такой слой позволяет осуществить идеальную (с позиций ГО) фокусировку преломленных и прошедших ГО лучей. Другими словами, плоский слой такой среды преобразует расходящийся фронт падающей цилиндрической волны в сходящийся цилиндрический фронт прошедшей волны. В современной научной литературе такой плоский слой получил название идеальной линзы Веселаго.

       В работе [2] подобный эффект был описан Р. Силиным для среды с . Первая экспериментальная работа, в которой изучалось влияние среды с отрицательной рефракцией, была осуществлена в 2000 г [3].

      Число публикаций, посвященных теоретическому и экспериментальному исследованию этой проблемы к настоящему времени весьма велико (см. [2-9] и цитируемую там литературу). Отметим, что теоретические работы основаны , как правило, на применении различных асимптотических методов – методе геометрической оптики (ГО) и различных ее модификаций или приближения Кирхгофа. Строгое решение ограничивается решением задачи для плоского бесконечного слоя или круглого бесконечного цилиндра из метаматериала.

      В данной работе мы впервые приводим результаты строгого численного решения двухмерной задачи рассеяния поля цилиндрической волны эллиптическим цилиндром из метаматериала и идеального проводящего эллиптического цилиндра, окруженного с зазором или без него слоем метаматериала конечной толщины. При этом учитывались потери среды .

ПОСТАНОВКА ЗАДАЧИ И ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

      Рассмотрим сначала задачу двухмерную задачу рассеяния цилиндрической Е поляризованной волны :

                                        (1)

конфокальной цилиндрической системой, состоящей из внешней диэлектрической оболочки внутри которой находится идеально проводящий цилиндр. Будем считать, что два контура , поперечного сечения диэлектрической оболочки (внешний и внутренний) описываются соответственно уравнениями:

             ,                                            (2)

               ,        ,                                    (3)

а контур поперечного сечения идеально проводящего металлического цилиндра задается уравнением:

                       ,                                           (4)

Отметим, что в случае совпадения контуров и мы имеем ситуацию, когда между диэлектрической оболочкой и металлическим цилиндром нет зазора. В противном случае между ними существует зазор свободного пространства с относительной диэлектрической проницаемостью и относительную магнитную проницаемость . Считается, что диэлектрическая оболочки имеет относительную диэлектрическую проницаемость и относительную магнитную проницаемость , т.е. представляет собой среду метаматериала с отрицательным показателем преломления (где величина - характеризует потери среды). Наконец ситуация, при которой рассеивает только оболочка из метаматериала , моделируется отсутствием металлического цилиндра с контуром (4).

     Входящие в выражения (1)- (4) величины представляют собой: {} – пространственные координаты точки наблюдения в цилиндрической системе координат; {} - пространственные координаты точки расположения источника волны (нить магнитного тока) в цилиндрической системе координат; величины , , (,) - характеризуют геометрию контуров (см. Рис. 1); - волновое число вакуума (свободного пространства), соответственно.

         Представим полное поле вне цилиндрических структур (2) - (4) в виде суперпозиции поля падающей волны (1) и рассеянного поля :

          = + ,           (5)



поле внутри оболочки из метаматериала обозначим , поле в области между оболочкой и металлическим цилиндром - соответственно.

          Как известно, поля , и должны удовлетворять соответствующим уравнениям Гельмгольца вне и внутри цилиндрической структуры (2) - (4), а также граничным условиям на контурах , и структуры (2) - (4), заключающимся в непрерывности полей ,, непрерывности их нормальных производных на соответствующих контурах и условию излучения на бесконечности (условию Зоммерфельда), т.е. являться решением граничной задачи. Для численного решение такой граничной задачи мы воспользуемся модифицированным методом дискретных источников (ММДИ) [10-12], который позволяет получить численное решение граничной задачи с контролируемой точностью. Используемое в этом методе представление для полей , и в виде суперпозиции полей вспомогательных цилиндрических источников, расположенных на вспомогательных контурах внутри и вне соответствующих контуров заведомо удовлетворяет уравнениям Гельмгольца и условию Зоммерфельда [10-12]. Пример, иллюстрирующий геометрию цилиндрической структуры металл-воздуз-метаматериал (3) и вспомогательных контуров , [10-12] представлен на Рис. 1 соответственно.

     Амплитудные коэффициенты для полей вспомогательных цилиндрических источников в методе ММДИ находятся из условия выполнения граничных условий в точках каждого контура.

       Точность решения задачи контролируется путем вычисления невязки граничных условий в точках, расположенных в середине между точками, где граничные условия выполняются точно (в таких точках граничные условия выполняются наихудшим образом [10-12]).

Рис. 1 Геометрия контуров для структуры металл-воздух-метаматериал (2)-(4) .



        Поскольку метод ММДИ и техника его применение к ряду задач с аналогичной конфигурацией контура рассеивающего тела описан достаточно подробно в работах [10-12], то мы не будем обсуждать особенности его применения в рассматриваемом случае, а лишь укажем, что приведенные ниже результаты расчетов диаграмм рассеяния имеют максимальную невязку граничных условий не превышающую величины для любой точки соответствующих контуров.

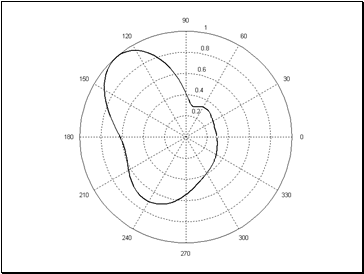
   Прежде, чем рассматривать задачу рассеяния цилиндрической структурой металл-воздух-метаматериал (2)-(4) приведем на Рис. 2 рассчитанную методом ММДИ нормированную диаграмму рассеяния одиночного идеально проводящего металлическим цилиндра (4).При расчетах полагалось, что параметры, характеризующие металлический цилиндр были равны: ; , а источник цилиндрической волны имел координаты: ; (что соответствует расположению источника волны в дальней зоне рассеивателя, т.к. >>). Из рисунка видно, что нормированная диаграмма рассеяния имеет два максимума. С позиции геометрической оптики (ГО) первый максимум соответствует направлению падения ГО луча на такой цилиндр, а второй – зеркально отраженному лучу ГО. Кроме того, минимальный уровень рассеянного поля имеет порядок и у диаграммы рассеяния отсутствуют интерференционные лепестки.

Рис. 2 Нормированная диаграмма рассеяния одиночного металлического

цилилндра с эллиптической формой поперечного сечения (; ).

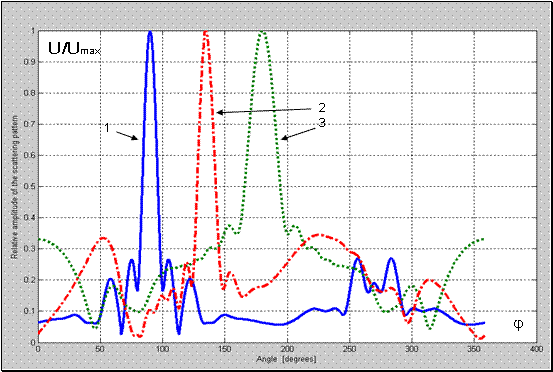
         На рис. 3 приведены результаты расчетов нормированной диаграммы рассеяния   структурой металл-воздух-метаматериал (2)-(4) с параматрами: ; ; ; ; ; (геометрия контуров такой системы изображена на Рис. 1); ; источник цилиндрической волны имел радиальную координату : ( т.е. фактически источник располагался в дальней зоне рассеивающей структуры) и три значения угловой координаты: ; и . 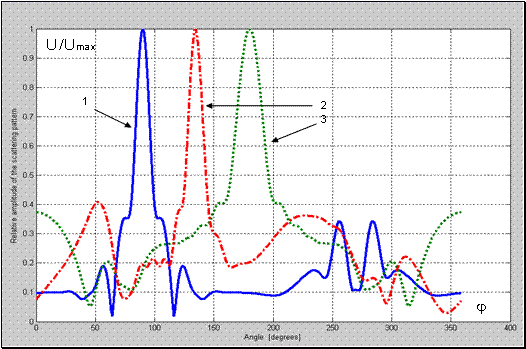Результаты расчетов для аналогичных значений параметров структуры металл-воздух-метаматериал и радиальной координате источника цилиндрической волны (), при которой он располагался на границе ближней и промежуточной зон структуры, представлены на Рис. 4.

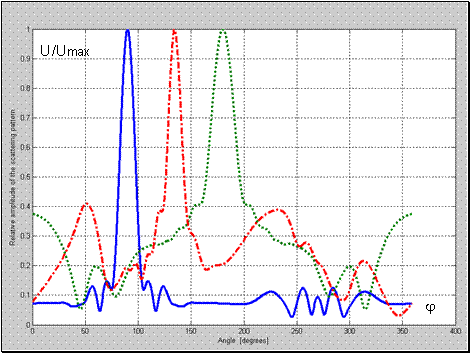
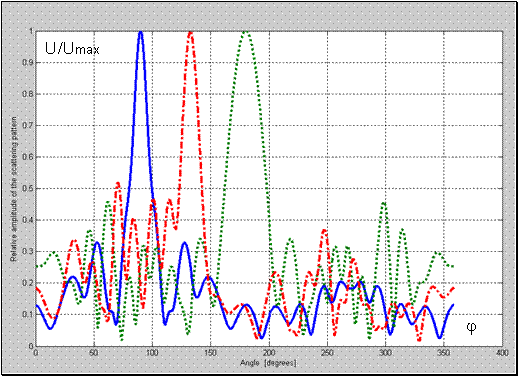
Рис. 3 Нормированная диаграмма рассеяния для структуры металл-воздух-метаматериал с ; ;    1-; 2-; 3- .



Из Рис.3, Рис. 4 следует, что наличие оболочки из метаматериала с зазором приводит к существенному изменению в структуре нормированной диаграммы рассеяния. Так при угле источника волны у нормированной диаграммы рассеяния появились колебания в области углов и . При этом уровень рассеянного назад поля (т.е. для углов ) стал на порядок меньше уровня рассеянного вперед поля (т.е. для углов ) при . При угле источника значительно вырос уровень поля в направлении угла 50 [град.] и так же появились колебания рассеянного поля.

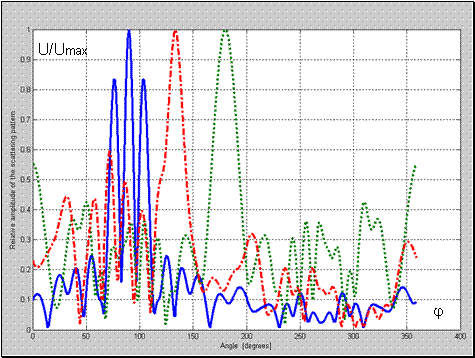
Рис. 4 Нормированная диаграмма рассеяния для структуры металл-воздух-метаматериал с ; ; 1- ; 2-; 3-.

        Отметим также на незначительные различия в структуре нормированной диаграммы рассеяния для случаев координат источника и , что оказалось характерным для всех случаев рассмотренных ниже. Поэтому ниже приводятся результаты расчетов только для случая радиальной координаты источника .

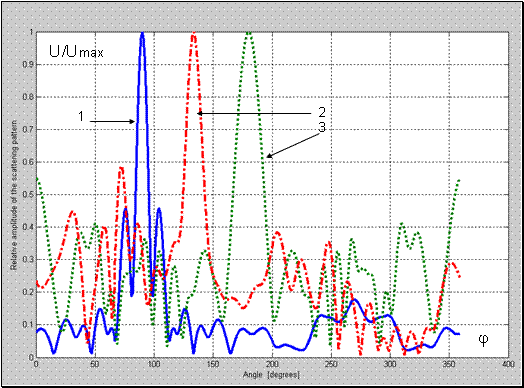
      Результаты расчетов нормированной диаграммы рассеяния для случая, когда метаматериал оболочки имеет показатель преломления , а все остальные параметры рассевающей системы остаются прежними представлен на Рис. 5

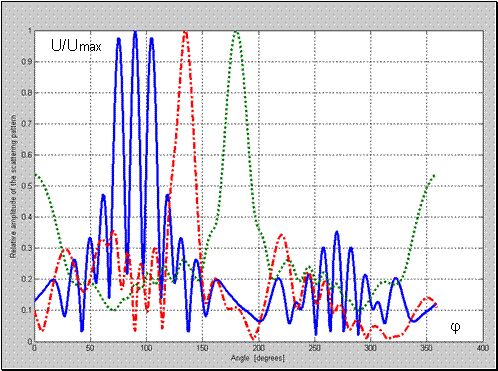
Рис. 5 Нормированная диаграмма рассеяния для структуры металл-воздух-метаматериал с ; ; 1- ; 2-; 3-.

     Здесь также характерным является различие на порядок уровня поля рассеянного вперед и назад при угле источника . По сравнению с рассмотренным выше случаем показателя преломления метаматериала здесь характерным является увеличение числа колебаний и разномасштабность уровня колебаний рассеянного поля.

         Увеличение числа и уровня колебаний присуще и случаю метаматериала с показателем преломления , представленным на Рис. 6.

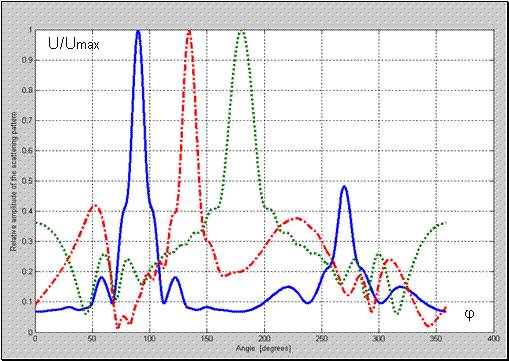
Рис. 6 Нормированная диаграмма рассеяния для структуры металл-воздух-метаматериал с ; ; 1- ; 2-; 3-.

Таким образом из приведенных выше результатов следует, что наличие оболочки из метаматериала с зазором сказывается на соотношении уровней рассеянного вперед и назад поля, и сопровождается развитием колебании диаграммы рассеяния.

        Для того чтобы лучше понять влияние оболочки из метаматериала на структуру диаграммы рассеяния рассмотрим ситуацию, когда в качестве рассеивающей системы выступает только сама оболочка из метаматериала, т.е. металлическое тело отсутствует внутри оболочки. При этом остальные параметры рассеивающей системы для , остаются прежними. На Рис. 7 – Рис. 9 представлены результаты расчетов нормированной диаграммы рассеяния для случаев показателя преломления ; и соответственно. Здесь характерным является развитие крупномасштабных осцилляций для рассеянного поля во всех трех случаях. Кроме того, при , и угловой координате источника уровень рассеянного назад поля на прядок ниже чем вперед.

Рис. 7 Нормированная диаграмма рассеяния для структуры воздух-метаматериал (оболочка из метаматериала) с ; ; 1- ; 2-; 3-.

Рис. 8 Нормированная диаграмма рассеяния для структуры воздух-метаматериал (оболочка из метаматериала) с ; ; 1- ; 2-; 3-.

Рис. 9 Нормированная диаграмма рассеяния для структуры воздух-метаматериал (оболочка из метаматериала) с ; ; 1- ; 2-; 3-.

       Теперь рассмотрим ситуацию, при которой оболочка из метаматериала вплотную (без зазора) покрывает металлический цилиндр (4), т.е. контура и совпадают. Рассчитанные нормированные диаграммы рассеяния для случаев показателя преломления ;   соответственно иллюстрируют Рис. 10, Рис. 11. Из рисунков следует, что в оболочки с зазором может существенно отличаться от случая оболочки без зазора. Так из данных Рис. 10 следует, что при угловой координате источника амплитуда поля рассеянное назад отличается в два раза, а не на порядок, как это было в случае оболочки с зазором.

Рис. 10 Нормированная диаграмма рассеяния для структуры металл-метаматериал с ; ; 1- ; 2-; 3-.

Рис. 11 Нормированная диаграмма рассеяния для структуры металл-метаматериал с;    ; 1- ; 2-; 3-.

   Из приведенных выше результатов численного решения задачи рассеяния цилиндрической волны структурами, содержащими оболочку конечной толщины, среда которой представляет собой метаматериал можно сделать следующие выводы:

   - наличие оболочки из метаматериала приводит к уменьшению на порядок отношения амплитуды поля рассеянного вперед и назад;

   - диаграмма рассеяния при этом характеризуется наличием локальных экстремумов, количество и величина которых зависит от толщины , значений показателя преломления и потерь оболочки

Работа выполнена при поддержке Российского Фонда Фундаментальных исследований (грант № 06-02-16804, № 06-02-16483).

Литература

1. V.G. Veselago, "Тhe Electrodynamics of Substances with Simultaneously Negative Values of and ", Sov. Phys. Usp., vol. 10, рр. 509, 1968.

2. Р. Силин, “Possibility of creating plane-parallel lenses ”, Opt. Spectrosc., 44,109,1978

3. D.R. Smith et а/., "Composite Medium with Simultaneously Negative Permeability and Permittivity", Phys. Rev. Lett., vol. 84, р. 4184, 2000.

4. J.B. Pendry and D.R. Smith, "Reversing Light with Negative Refraction", Physics Today, June 2004, рр. 37, 2004.

5. J.B. Pendry, ''Negative Refraction Makes а Perfect Lens", Phys. Rev. Lett., vol. 85, рр. 3966, 2000.

6. GW. 't Hooft, "Comment оп ''Negative Refraction Makes а Perfect Lens"", Phys. Rev. Lett., vol. 87, рр. 249701.1, 2001.

7. George V. Eleftheriades, Ashwin К. Iyer and Peter С. Кremer, Planar Negative Refractive Index Media Using Periodically L-C Loaded Transmission Lines, IEEE Tr.MTT,vol.50,N 12, pp. 2702, December 2002

8.Шевченко В.В., Об обратных плоских волнах в однородных изотропных средах, РЭ, т.48, N 10, с. 1202, 2003.

9. Dorofeenko A.V., Lisyansky A.A., Merzlikin A.M.,Vinogradov A.P., Full-wave analysis of imaging by the Pendry-Ramakrishna stackable lens, Physical Review,2006, B 73, 235126-1 - 235126-1-6.

10. A.P. Anioutine, A.G. Kyurkchan, S.A. Minaev, About universal modification to the method of discrete sources and its application, JQSRT, Vol. 79-80, pp.509, 2003

11. А.П. Анютин, А.Г. Кюркчан, С.А. Минаев, О новой модификации метода дискретных источников, Радиотехника и Электроника, т.47, N 6, c.688, 2002

12. A.P. Anioutine, A.G. Kyurkchan, S. A. Manenkov, S.A. Minaev, About 3D solution of diffraction problems by MMDS, JQSRT, v.100, N1-3, pp.26, 2006 (July/Augest).