УДК  621.3.049.7.029

Модель накопления повреждений интегральными микросхемами в электромагнитных полях  импульсного радиоизлучения

 

А. В. Ключник¹, Ю. А. Пирогов², А. В. Солодов¹

¹¹Федеральное государственное унитарное предприятие “Московский радиотехнический институт Российской Академии наук”,

²Московский государственный университет им. М.В.Ломоносова, Центр магнитной томографии и спектроскопии

 

Получена 29 июня 2010 г.

Аннотация. Представлены  результаты анализа влияния накопления тепла в кристалле ИМС, при воздействии последовательности импульсов радиоизлучения, на формирование дефектов в структуре ИМС и вероятность её повреждения.

Ключевые слова: модель, накопление, повреждение, интегральные микросхемы, радиоимпульс.

Введение

Интенсивные электромагнитные помехи могут приводить к отказам чувствительных радиоэлементов, в первую очередь, интегральных микросхем (ИМС). Чувствительность радиоэлементов к воздействию интенсивных импульсов радиоизлучения определяется интенсивностью излучения, длительностью импульсов t и частотой их повторения F. В режиме моноимпульсного облучения механизмы повреждения достаточно хорошо изучены [1-5]. Однако в полиимпульсном режиме облучения механизмы повреждения исследованы значительно меньше. Экспериментально установлено [6-8], что под действием мощных повторяющихся радиоимпульсов в значительном числе случаев наблюдается ухудшение характеристик микросхем «от импульса к импульсу». При высокой частоте повторения этот эффект можно было бы объяснить накоплением тепла от импульса к импульсу. Однако для накопления тепла необходима высокая частота повторения импульсов, а эффект наблюдается и в том случае, когда за время паузы между импульсами температура на чувствительном элементе микросхемы возвращается к исходному значению, например, на частотах повторения в десятки и сотни герц и скважности Q~10⁵.

Повреждение элемента ИМС в режиме одиночного импульса происходит при энергии и мощности импульса больших, чем в полиимпульсном режиме, а вероятность повреждения значительно возрастает. Причем мощность радиоимпульса, приводящего к повреждению, уменьшается с увеличением частоты повторения импульсов. Полученные экспериментальные результаты могут в значительной степени быть объяснены в рамках представленной в работе модели накопления повреждений [7].

В работе [8] был рассмотрен один изолированный p-n переход на кристалле. Если ИМС находится во внешнем поле, то интенсивная высокочастотная наводка формируется одновременно на всех выводах микросхемы и рассеивается на большом числе элементов, в том числе на p-n переходах, токоведущих линиях, контактных площадках. Из-за этого радикально меняются тепловые режимы, а также статистические особенности эффектов повреждения. В настоящей работе выполнено решение тепловой задачи для кристалла микросхемы, содержащей большое число элементов тепловыделения, проведен учет влияния перекрытия тепловых потоков от разных элементов на нагрев кристалла ИМС. Проведена оценка частот повторения, при которых происходит накопление тепла. В рамках модели накопления повреждений выполнена оценка вероятности формирования дефектов в структуре ИМС и ее повреждения при разных частотах повторения импульсов.

  

Модель накопления повреждений

Существующие теории статистических отказов полупроводниковых элементов разработаны для случаев достаточно медленных, деградационных процессов (диффузия, электромиграция и т.д.). В представленной в работе [7] модели накопления повреждений  рассмотрены, «катастрофические» отказы под действием перегрузок, которые многократно превосходят рабочие параметры номинальных сигналов ИМС. Наиболее распространенными механизмами повреждения ИМС являются вторичный пробой, плавление металлизации, пробой диэлектрика.

Вторичный (тепловой) пробой в режиме коротких высокочастотных импульсов связан с попаданием рабочей точки в область электрического пробоя (на обратной ветви ВАХ), резким увеличением тока через прибор значительным тепловыделением в области p-n перехода и последующим тепловым повреждением структуры. Чаще всего наблюдается проплавление локальных областей эмиттера входных транзисторов и p-n переходов защитных диодов.

Плавление токоведущих линий обычно наблюдается на углах.

Пробой диэлектрика наблюдается в затворах КМОП ИМС, когда напряжение на затворе достигает величины, определяемой электрической прочностью материала окисла.

Все механизмы имеют низкие пороги возникновения из-за малых геометрических размеров характерных областей в ИМС и наличия дефектов.

В модели накопления повреждений  [7] предполагается, что под действием одного импульса происходит незначительное локальное изменение структуры ИМС, например, образование дефекта структуры выпрямляющего контакта диода, которое приводит к изменению его характеристик. Такой характеристикой может быть, например, дифференциальная проводимость p(t) выпрямляющего контакта. Дефектами могут быть области локального плавления полупроводниковой структуры (или токоведущей линии). Выход прибора из строя будет происходить при достижении некоторого критического числа дефектов и при достижении некоторого критического значения p(t)=p_c. С использованием активационной теории Аррениуса, в работе [8] получено кинетическое уравнение для параметра p(t), описывающее процесс повреждения p-n перехода в ИМС:

.                               (1)

Здесь Е_а – энергия активации, r - постоянная, зависящая от типа дефектов, k - постоянная Больцмана, T=T(t)  – температура выпрямляющего контакта. Член n×p(t), описывает процесс восстановления полупроводниковой структуры.

При импульсно-периодическом режиме тепловыделения с длительностью прямоугольных импульсов t и частотой повторения F, изменение параметра p(t) под действием пачки из N импульсов принимает вид:

            (2)

здесь T_j(t)  – температура выпрямляющего контакта, в процессе воздействия j-го импульса.

Повреждение и образование дефектов в структуре p-n перехода обусловлено его интенсивным разогревом под действием радиоимпульсов. Температура выпрямляющего контакта T_j(t) в уравнении (2) может быть определена из решения уравнения теплопроводности. Источниками тепловыделения на кристалле ИМС является большое число элементов, расположенных на его внешней поверхности. Тепловыделение обусловлено рассеянием высокочастотной наводки, сформированной на выводах ИМС, источниками тепловыделения являются р-n переходы, резисторы, токоведущие линии и т.д. Полную мощность всех источников можно оценить из соотношения P~S_ЭФФ×ППЭ, где S_ЭФФ - эффективная площадь микросхемы, примерно равная геометрической площади, определенной по внешнему периметру контактов ИМС. Для цифровых ИМС среднее расстояние между элементами на поверхности кристалла составляет w» 10...20 мкм. Для микросхем с высокой степенью интеграции это расстояние составляет несколько микрометров. Из решения уравнения теплопроводности следует, что на малых временах t<t_w=w²/4k (k - температуропроводность полупроводника) каждый из источников тепловыделения может рассматриваться независимо от других, а на временах t>t_w=w²/4k (k - температуропроводность полупроводника) тепловые потоки от источников перекрываются и формируют почти плоский тепловой фронт, распространяющийся к нижней поверхности кристалла. Тепловая постоянная t_w составляет единицы микросекунд. Таким образом, при решении тепловой задачи на временах больших t_w можно считать, что источник тепловыделения имеет равномерную плотность и расположен в слое толщиной w на внешней поверхности кристалла. Плотность мощности можно оценить из соотношения q=P/(Sw), где P - суммарная мощность источников тепловыделения (постоянна в течение действия импульса), S – площадь верхней поверхности ИМС, где расположены источники тепловыделения.

Верхняя и боковые поверхности кристалла теплоизолированы, а на нижней поверхности имеется идеальный тепловой контакт с корпусом микросхемы и поддерживается постоянная температура Т₀. Так как толщина кристалла ИМС D = 0,2…0,4 см значительно меньше его продольных размеров

Для решения тепловой задачи в этом случае может быть использована простая модель, в которой все источники тепловыделения равномерно распределены в слое толщиной w и имеют мощность тепловыделения равную суммарной мощности всех источников. Таким образом, мы может оценить температуру к моменту начала следующего импульса (величину T_j) тепловыделения при условии, что пауза между импульсами значительно превосходит t_w.

Распределение температуры T(x,t) определялось из уравнения теплопроводности для кристалла кремния толщиной D, с теплоизолированной верхней границей (¶T(0,t)/¶x=0), с фиксированной температурой на нижней границе T(D,t)=T₀ (нижняя часть кристалла находится в контакте с теплоотводящей поверхностью) и с начальным условием T(x,0)=T₀. Источники тепловыделения располагались в слое толщиной w с равномерной плотностью q(x,t)=(q(x)-q(x-w))×q(t)/2, q(x)- функция (q(x)=1, если x>0, q(x)=0, если x£0) около теплоизолированной грани кристалла. В продольном направлении структура считалась неограниченной.

Уравнение теплопроводности

,

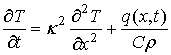k²=l/(Cr).

Представленная краевая задача решалась в симметричной области –D<x<D (это обеспечило граничное условие на теплоизолированной поверхности) методом разделения переменных [9], результат имеет вид

T(x,t)=T₀+åc_n×cos(k_nx)×c_n(t), c_n(t)=òexp[-a_n(t-t’)] q(x,t’)dt’/(Cr),

c_n=2sin(k_nw)/(k_nD), k_n=p(n+1/2)/D, a_n=k²×k_n²

Для полиимпульсного источника тепловыделения с длительностью импульса t и длительностью паузы t_п на верхней границе кристалла после прохождения N импульсов

c_n(t)=q/(Cr)×[1-exp(-a_nt)]/a_n×[1-exp(-a_nNT)]/[1-exp(-a_nT)]×exp(-a_nDt)

Здесь T=1/F=t+t_П – период повторения импульсов, Dt=t-t_N - время после окончания N-го импульса.

Под действием теплового импульса длительностью t температура на верхней границе кристалла (x=0) будет возрастать и к моменту его окончания увеличится на . После окончания теплового импульса температура на поверхности кристалла падает и к моменту прихода следующего импульса она будет отличаться от своего исходного значения T₀ на dТ. Величина dТ определяется соотношениями между длительностью импульса t, длительностью паузы t_П и двумя тепловыми постоянными t_w и 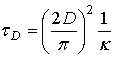. В зависимости от частоты повторения импульсов, реализуется два разных тепловых режима – режим с накоплением тепла от импульса к импульсу и режим, в котором накопления тепла не происходит.

Рассмотрим два этих режима более детально. Нас будет интересовать случай коротких импульсов t _w<t <t_D.

Для частот повторения импульсов F<1/t_D,  к моменту прихода второго импульса величина тепловой добавки убывает экспоненциально,
dТ~exp(-1/Ft_D). Таким образом, при такой частоте повторения импульсов тепловой добавкой можно пренебречь  и накопления тепла не происходит.

Для частот повторения импульсов F³1/t_D  характер изменения добавки температуры dТ в зависимости от частоты повторения импульсов совершенно иной. В пределе F>>1/t_D температура в паузе между импульсами убывает степенным образом и к моменту прихода второго импульса dТ~∆T_1н(Ft)^1/2. Таким образом, к моменту прихода каждого следующего импульса температура не успевает снизиться до температуры Т₀, происходит накопление тепла от импульса к импульсу и температура будет увеличиваться.  И через время t»t_D после начала воздействия установятся колебания температуры: к окончанию действия тепловых импульсов температура увеличится на »∆T_1н, а в паузе между импульсами снизиться почти до постоянного значения ». 

Подставим в (2) полученную зависимость температуры от времени. В результате для частот повторения импульсов F<1/t_D,, для параметра p_N, получаем следующую оценку:

,            (3)

,                                 

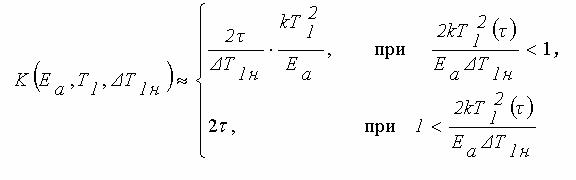где

   ,

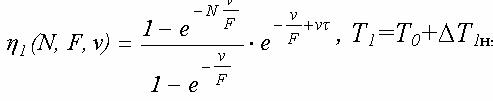В этом случае, когда частот повторения импульсов F³1/t_D, изменение параметра p(t) под действием пачки из N импульсов принимает вид:

    (4)

,

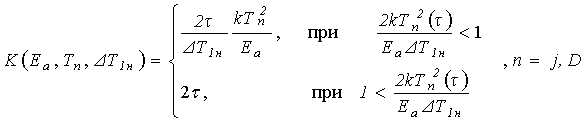где ,, ,

.

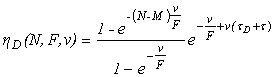Повреждение прибора происходит при достижении параметром p_N некоторого критического значения p_c.

Считаем, что статистические флуктуации параметра p связаны со случайной величиной активационной энергии Е_а, и именно ее флуктуации определяют статистику повреждений (так как дефекты, образующиеся под действием серии импульсов перегрузки, могут возникать на различных центрах, кроме того, меняться условия образования дефектов).

Если для случайной непрерывной величины Е_а, известна плотность вероятности f(Е_а), то вероятность повреждения ИМС W можно оценить как вероятность превышения параметром p (после воздействия N импульсами перегрузки) критического значения ∆p_c:

.

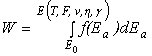E(T,F,n,h,g) определяется из решения уравнений (3), (4) при p_N=p_c, где вводится обозначение g=ln(rt/p_c).

Для оценки вероятности повреждения ИМС предположим, что энергия активации Е_a имеет равномерное распределение в области E_o£Е_a£E_o+D. Тогда вероятность повреждения (превышения р_с) будет иметь вид:

W=0,                                          если E(T,F,n, h,g) <E_o

(5)

,         если E_o £ E(T,F,n, h,g) £E_o +D,

W=1,                                           если E(T,F,n, h,g) >E_o+D.

Представленная модель дает возможность рассчитать зависимость вероятности повреждения W, например, от числа тепловых импульсов N, от частоты повторения импульсов F, от мощности P (или энергии) одного импульса и т.д.

Величину E_o можно оценить как kT_c, где T_c»(T₀+DT_с) - критическое значение температуры, используемое  в модели Вонша-Белла, при достижении которого происходит повреждение p-n перехода. Величину DT_с для разных p-n переходов, например,  кремниевых ИМС можно определить по эмпирическому выражению, приведенным в работе [3]. Так для переходов эмиттер-база с напряжением лавинного пробоя -7…-9 В, DT_с »350…500⁰.

Величина E_o+D  может определяться процессами, например, нагревом до температуры плавления и расплавлением p-n перехода (полностью или частично). Поэтому параметр D/E_o, который характеризует разброс активационной энергии на разных дефектах p-n перехода, может быть достаточно большим.

На рис. 1 представлена полученная зависимость вероятности повреждения p-n перехода микросхем W от числа воздействующих радиоимпульсов N. Графики на рис. 1 построены при E_o=kT_c=k(T₀+DT_c), T₀»300⁰С, DT_c=500⁰С, D/E_o=7,  g=5,  t=1мкс, n=0,01 Гц, F=100 Гц. Для графика  1– DT_1н=150⁰,  2 – DT_1н=350⁰.

Из выражений (3) - (5) следует, что при n/F,Nn/F<<1 вероятность повреждения W пропорциональна log(N) и нарастает с увеличением количества воздействующих импульсов, а при Nn/F>>1 вероятность W стремится к постоянной величине.

Из анализа рис. 1 видно, что для реально возможных температур перегрева ИМС и при сравнительно небольших вариациях параметров распределения активационной энергии теоретические кривые хорошо согласуются с результатами работы [8] и аппроксимируют результаты статистической обработки экспериментальных исследований представленные на рис. 1 работы [7].

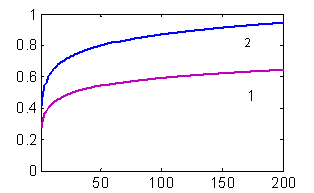
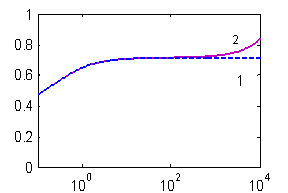
На рис. 2 представлена зависимость вероятности повреждения микросхем W от относительной частоты повторения импульсов F. Графики на рис. 2 построены при E_o=kT_c, T_с=800⁰С, DT_1н=200⁰С, t=1 мкс, N=200, D/E_o=7, g=5, t=1мкс, n=0,01 Гц. Графики построены без учета накопления тепла (1) и  с учетом накопления тепла (2).

Рис. 1	Рис. 2

Из графика 2 рис.2 видно, что для частот повторения импульсов F³1/t_D (t_D»1 мс) происходит накопление тепла от импульса к импульсу, но из-за большой скважности 1/Ft увеличение вероятности повреждения  становится заметным только на частотах F³3×10³Гц.

Если зафиксировать вероятность повреждения на уровне 0,5  в выражении (5),  то можно определить зависимость относительной мощности Р/Р_с импульса от частоты повторения импульсов F. Полагая E_o=kT_c , для наиболее интересного случая Nn/F<<1 получим

.               (7)

Из формулы (7) следует, что с увеличением частоты F мощность Р_0,5 (энергия Е_0,5=P_0,5t) импульса, необходимая для повреждения прибора, уменьшается. Если при этом Ft_D <1, то энергия может уменьшаться даже в области тех частот F, где нет еще  накопления тепла от импульса к импульсу.

Выводы

Представленные результаты показывают, что при вероятностном характере повреждения микросхем под воздействием пачки радиоимпульсов, возможны повреждения одновременно нескольких ее элементов. Выход из строя каждого из поврежденных элементов микросхемы может рассматриваться на основе модели накопления повреждений и происходит при достижении некоторого критического числа дефектов, формирующихся под действием каждого импульса в пачке.

Построенная кумулятивная модель накопления повреждений, позволяет описывать зависимость мощности повреждения микросхем от числа воздействующих радиоимпульсов N, их мощности P (или энергии) и частоты повторения F (с учетом возможного накопления тепла от импульса к импульсу).

 

Литература

1.                   Риккетс Л.У., Дж. Э. Бриджес, Дж. Майлетта. Электромагнитный импульс и методы защиты. М., Атомиздат, 1979.

2.                   G.C.Messenger, M.S.Ash. «The Effects of Radiation on electronic systems», N.Y., 1986.

3.                   Антипин В.В., Годовицын В.А., Громов Д.В., Кожевников А.О., Раваев А.А. Влияние мощных импульсных микроволновых помех на полупроводниковые приборы и интегральные микросхемы. // Зарубежная радиоэлектроника.-1995. №1.-С. 37-52.

4.                   Waunch D.C., Bell R.R. Determination of threshold failure levels semiconductor diodes and transistors due to pulse voltage. // IEEE Trans. Nucl. Sciens.-1968.-Vol. NS - 15, N6.-P. 244-259.

5.                    Tasca D.M. Pulse power failure modes in semiconductors. // IEEE Trans. Nucl. Sciens. – 1970. – Vol. NS-17, N2. – P. 364-372.

6.                   Васильев К.Б., Ключник А.В., Солодов А.В. Повреждение цифровых интегральных под действием импульсного радиоизлучения. // Тезисы докладов на 11-й Междунар. Крымская конфер. «СВЧ-техника и телекоммуникационные технологии», Севастополь, 2001, - С.300

7.                   Васильев К.Б., Ключник А.В., Солодов А.В. Статистика отказов цифровых ИМС, вызванных импульсным радиоизлучением. // Тезисы докладов на 9-й Междунар. Крымская конфер. «СВЧ-техника и телекоммуникационные технологии», Севастополь, 1999, - С.329-330.

8.                   Ключник А.В., Солодов А.В. Статистическая модель повреждения цифровых интегральных микросхем импульсным радиоизлучением. // Радиотехника. – 2010. №2. – С.37-41.

9.                   Тихонов А.Н., Самарский А.А. Уравнения математической физики.- М.: Наука, 1972.
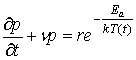
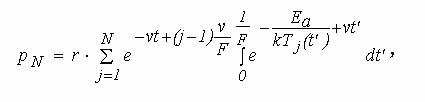
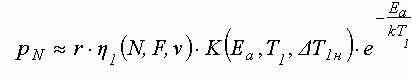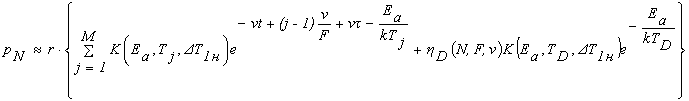
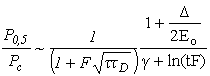