УДК 537.874
ДЕТЕКТОР МОДУЛИРОВАННОГО ТЕРАГЕРЦЕВОГО ИЗЛУЧЕНИЯ НА ОСНОВЕ ГРАФЕНОВЫХ НАНОЛЕНТ
Ю. В. Стебунов1, В. Г. Лейман1, А. В. Арсенин1, В. Л. Семененко1, В. И. Рыжий2
1 Московский физико-технический институт (государственный университет), Лаборатория нанооптики и фемтосекундной электроники
2 Университет Тохоку, Сендай, Япония
Получена 12 июня 2012 г.
Аннотация. Предложена новая схема детектора модулированного терагерцевого излучения с рекордно высокой частотой модуляции (вплоть до нескольких ГГц). Детектор базируется на наномеханическом резонаторе, в котором в качестве подвижного элемента используется достаточно узкая графеновая нанолента. Движение графеновой наноленты обусловлено действием пондеромоторной силы, возникающей вследствие возбуждения в системе плазмонного резонанса. Предлагаемый детектор обладает рядом преимуществ по сравнению с ранее предложенными устройствами такого типа, например, более высокой чувствительностью и возможностью перестройки частоты модуляции в широком диапазоне.
Ключевые слова: графеновая нанолента, углеродная нанотрубка, терагерцевое излучение, плазмонный резонатор, демодулятор, детектор.
Abstract. We proposed a novel scheme of the detector of terahertz radiation modulated by megahertz or gigahertz signals. Detector model is based on the nanomechanical resonator with the sufficiently narrow graphene nanoribbon as a mechanically moving part. Motion of a nanoribbon is supported by the electromagnetic ponderomotive force appearing due to the plasmon resonance exited in the system. Using developed model we obtained that the proposed demodulator has a number of advantages such as higher output signal and higher modulation frequency of incoming radiation in comparison with the previously proposed demodulators of terahertz radiation.
Keywords: graphene nanoribbon, carbon nanotube, terahertz radiation, plasmon resonator, demodulator, detector.
Введение
В последние годы технологии, связанные с терагерцевым излучением, привлекают все больше внимания. Потенциальное применение терагерцевого излучения продемонстрировано в различных областях [1]. Однако, использование терагерцевого излучения затруднено из-за отсутствия удобных, компактных и надежных источников и детекторов, а также других устройств, необходимых для работы с таким излучением [2]. Тем не менее, одним из наиболее перспективных применений модулированного терагерцевого излучения является его использование для передачи информации [3]. Ключевыми устройствами, использующимися для процесса передачи информации, являются детекторы и демодуляторы излучения. Недавно были предложены высокоэффективные детекторы модулированного терагерцевого излучения, основанные на идее транзистора с механически подвижным затвором [4-9], впервые сформулированной в работе [10] для приборов радиодиапазона. Работа таких устройств основана на том факте, что геометрическое положение затвора влияет на ток, протекающий в канале транзистора. В ранее представленных работах роль канала в детекторах терагерцевого излучения выполнял двумерный электронный газ в полевом транзисторе с высокой подвижностью электронорв и рассматривалось влияние затвора на плазменные волны в канале [4-8]. В работе [9] была рассмотрена модель детектора терагерцевого модулированного излучения, в которой подвижный затвор и канал для плазменных колебаний объединены в одной углеродной нанотрубке (УНТ). В этой работе было показано, что детекторы на УНТ обладают лучшими параметрами по сравнению с детекторами на основе двумерного электронного газа.
В представленной работе предлагается детектор модулированного терагерцевого излучения на основе узких графеновых нанолент (ГНЛ), в которых возбуждаются плазменные волны ‑ плазмоны (рис. 1). Возможность возбуждения плазмонов в ГНЛ была подтверждена экспериментально [11]. Также было показано, что достаточно узкие (ГНЛ) представимы в виде квантовых нитей [12]. Одним из возможных подходов к описанию плазмонов в квантовых нитях является использование модели жидкости Томонаги-Латтинжера (ЖТЛ) [13]. В рамках этой модели распространение сигнала а ГНЛ описывается уравнениями передающей линии, в которую включены дополнительные элементы, учитывающие квантовые свойства электронов в рассматриваемых системах [14-15] (рис. 2). Стоит отметить также тот факт, что рекордные параметры рассматриваемого детектора обусловлены уникальными механическими свойствами графеновых нанолент [16]. Были экспериментально получены наноэлектромеханические резонаторы на ГНЛ с резонансными частотами в мегагерцевом и даже гигагерцевом диапазонах [17-25].
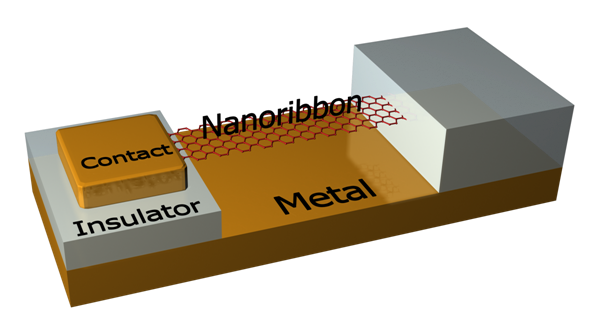
Рис. 1. Общий вид рассматриваемого
устройства.

Рис. 2. Эквивалентная схема передающей линии в модели ГНЛ
как жидкости Томонаги-Латтинжера.
.
Принципы работы демодулятора на основе графеновых нанолент
Предлагаемый детектор амплитудно-модулированного терагерцевого излучения представляет собой закрепленную на концах ГНЛ, подвешенную над проводящей плоскостью (рис. 1). ГНЛ и проводящая плоскость под ней формируют конденсатор, в котором возникает пондеромоторная сила, действующая на ГНЛ. Эта сила возбуждает механические колебания ГНЛ на частоте модуляции терагерцевого излучения. Таким образом, механический резонатор (упругая графеновая лента) и электромагнитный резонатор (плазменный осциллятор в отрезке графеновой ленты, или плазмон) оказываются связанными. Между ГНЛ и металлической поверхностью прикладывается базовое напряжение. Следовательно, колебания наноленты наводят во внешней цепи переменный ток (наведенный ток), являющийся выходным сигналом детектора. Амплитуда этого тока пропорциональна квадрату амплитуды напряжения установившегося плазмона, глубине модуляции падающего излучения и базовому напряжению.
Модель жидкости Томонаги-Латтинжера для описания динамики элекронов в ГНЛ
Как уже говорилось
выше, модель жидкости Томонаги-Латтинжера позволяет представить распространение
плазмонов в ГНЛ как процесс распространения волн в обычной передающей линии
(ПЛ), но в которую необходимо добавить несколько дополнительных элементов [14-15]
(рис. 2). В случае ГНЛ в эквивалентную схему передающей линии вводятся такие
величины, как погонная квантовая емкость ![]() , погонная кинетическая
индуктивность
, погонная кинетическая
индуктивность ![]() и квантовое сопротивление
и квантовое сопротивление ![]() (h
– постоянная планка, e –
заряд электрона,
(h
– постоянная планка, e –
заряд электрона, ![]() ‑ скорость Ферми) в
дополнение к погонным электрической емкости
‑ скорость Ферми) в
дополнение к погонным электрической емкости ![]() и
магнитной индуктивности
и
магнитной индуктивности ![]() .
Уравнения, описывающие получаемую передающую линию, могут быть представлены в
следующей форме:
.
Уравнения, описывающие получаемую передающую линию, могут быть представлены в
следующей форме:
![]() (1)
(1)
где ![]() и
и ![]() –
распределения напряжения и тока вдоль цепи по оси x. В системе
уравнений (1) введены следующие обозначения:
–
распределения напряжения и тока вдоль цепи по оси x. В системе
уравнений (1) введены следующие обозначения:
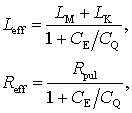
где ![]() ,
,
![]() – длина свободного пробега электрона. Длина ГНЛ предполагается равной
нечетному числу четвертей длины волны плазмона. Известно, что подобная
разомкнутая передающая линия эквивалентна последовательному колебательному LCR -
контуру [26]. Для определенности, в дальнейшем рассматривается проводящая линия
с длиной, равной одной четверти длины волны плазмона. Амплитуду
– длина свободного пробега электрона. Длина ГНЛ предполагается равной
нечетному числу четвертей длины волны плазмона. Известно, что подобная
разомкнутая передающая линия эквивалентна последовательному колебательному LCR -
контуру [26]. Для определенности, в дальнейшем рассматривается проводящая линия
с длиной, равной одной четверти длины волны плазмона. Амплитуду ![]() напряжения стоячей плазменной волны в
передающей линии можно представить в виде:
напряжения стоячей плазменной волны в
передающей линии можно представить в виде: ![]() , где
, где ![]() –
амплитуда падающего терагерцевого излучения,
–
амплитуда падающего терагерцевого излучения,
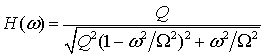 (2)
(2)
‑ амплитудно-частотная характеристика контура. Здесь ![]() –
добротность плазменного резонатора,
–
добротность плазменного резонатора, ![]() – его резонансная
частота. Для типичных параметров рассматриваемой системы (расстояние между ГНЛ
и проводящей плоскостью
– его резонансная
частота. Для типичных параметров рассматриваемой системы (расстояние между ГНЛ
и проводящей плоскостью ![]() длина ГНЛ –
длина ГНЛ –
![]() ширина ГНЛ
ширина ГНЛ ![]()
![]() ,
, ![]()
![]()
![]()
![]() ), с учётом
квантового сопротивления, получаем:
), с учётом
квантового сопротивления, получаем: ![]() и
и ![]() .
.
Механические колебания ГНЛ с закрепленными концами
Графен и различные
структуры на его основе – уникальные материалы для наноэлектромеханических
систем (НЭМС) из-за их рекордных механических параметров [16]. Различные
механические резонаторы, основанные на графене, хорошо изучены как
теоретически, так и экспериментально [17-25]. Одна из самых распространённых теоретических
моделей, описывающая механические свойства графена, основывается на теории
упругости сплошных сред, в рамках которой вводятся такие параметры монослоя
графена, как модуль Юнга E, коэффициент Пуассона ![]() , плотность массы
, плотность массы ![]() и толщина монослоя t [22]. В дальнейших
оценках приняты следующие значения этих параметров:
и толщина монослоя t [22]. В дальнейших
оценках приняты следующие значения этих параметров: ![]() ,
, ![]() ,
, ![]() и
и ![]() [27].
Одним из преимуществ ГНЛ по сравнению с УНТ является возможность возбуждения в
механических резонаторах на ГНЛ не только поперечных (изгибных) [17-20,
22-25],
но и крутильных колебаний [21]. Теория упругости дает решения для различных
колебательных мод ГНЛ [28]. Так, например, получены частоты для поперечных
колебательных мод –
[27].
Одним из преимуществ ГНЛ по сравнению с УНТ является возможность возбуждения в
механических резонаторах на ГНЛ не только поперечных (изгибных) [17-20,
22-25],
но и крутильных колебаний [21]. Теория упругости дает решения для различных
колебательных мод ГНЛ [28]. Так, например, получены частоты для поперечных
колебательных мод – ![]() (
(![]() – решения
уравнения
– решения
уравнения ![]() ) и для крутильных колебательных мод –
) и для крутильных колебательных мод – ![]() (
(![]() –
целое). Стоит также отметить, что для рассматриваемых размеров ГНЛ частоты низших
резонансных мод для крутильных колебаний на два порядка больше, чем для поперечных
колебаний. Так, для поперечных колебаний
–
целое). Стоит также отметить, что для рассматриваемых размеров ГНЛ частоты низших
резонансных мод для крутильных колебаний на два порядка больше, чем для поперечных
колебаний. Так, для поперечных колебаний ![]() для крутильных колебаний
для крутильных колебаний ![]() .
.
Уравнение движения ГНЛ
Вследствие того, что кинетическая индуктивность в рассматриваемой системе значительно больше магнитной индуктивности, здесь и везде далее магнитная составляющая электромагнитной энергии не учитывается.
В случае поперечных колебаний ГНЛ сила, действующая на единицу её длины, равна [9]:
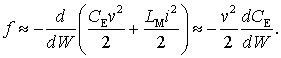 (3)
(3)
Здесь ![]() ,
где
,
где ![]() частота модуляции падающего излучения.
частота модуляции падающего излучения.
В случае крутильных колебаний погонный момент сил, приложенных к ГНЛ, равен
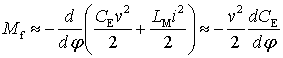 (4)
(4)
Таким образом, как сила, так и момент пондеромоторной силы зависят от изменения емкости системы при изгибе или кручении ГНЛ. Для рассматриваемой системы электрическую емкость можно рассчитать численными методами (например, методом конечных разностей). В данном случае коммерческой программой COMSOL Multiphysics рассчитана двумерная система, состоящая из эквипотенциальной пластины, расположенной над заземленной проводящей поверхностью.
Емкость системы была вычислена как функция положения пластины, определяемая в случае поперечных колебаний расстоянием между пластиной и заземленной поверхностью (рис. 3), а в случае крутильных колебаний ‑ углом поворота пластины относительно ее оси симметрии (рис. 4). Стоит отметить, что в случае крутильных колебаний производная емкости по углу поворота максимальна в случае, когда пластина уже имеет определённый угол наклона при отсутствии сигнала. Таким образом, для достижения максимальной чувствительности при проектировании устройства нужно задать этот начальный угол наклона.
В рамках рассматриваемой модели уравнение движения ГНЛ в случае поперечных колебаний имеет вид:
![]() (5)
(5)
где ![]() –
изменение расстояния между ГНЛ и металлической поверхностью (так что
–
изменение расстояния между ГНЛ и металлической поверхностью (так что ![]() ,
, ![]() –
расстояние в равновесном положении),
–
расстояние в равновесном положении), ![]() –
коэффициент затухания поперечных колебаний.
–
коэффициент затухания поперечных колебаний.
Уравнение движения ГНЛ в случае крутильных колебаний
![]() (6)
(6)
где ![]() изменение
угла поворота колеблющейся ГНЛ,
изменение
угла поворота колеблющейся ГНЛ, ![]() коэффициент
затухания крутильных колебаний,
коэффициент
затухания крутильных колебаний, ![]() момент
инерции ГНЛ относительно ее оси симметрии.
момент
инерции ГНЛ относительно ее оси симметрии.
Решения уравнений (5) и (6) соответственно:
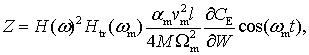 (7)
(7)
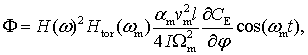 (8)
(8)
где
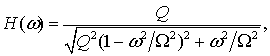 (9)
(9)
амплитудно-частотная характеристика гармонического осциллятора.
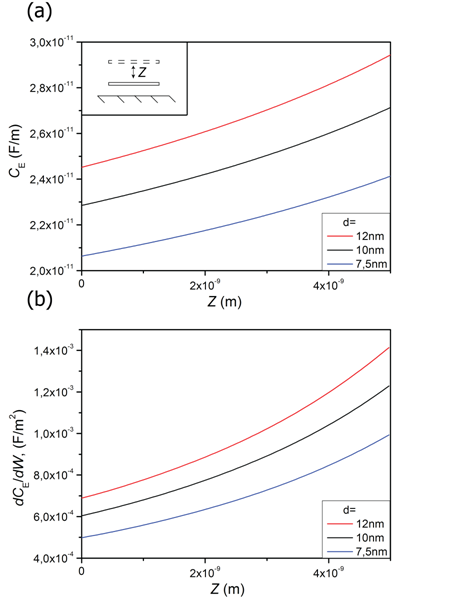
Рис. 3. Емкость системы (a) и производная емкости системы (b), как функции поперечного смещения графеновой наноленты.
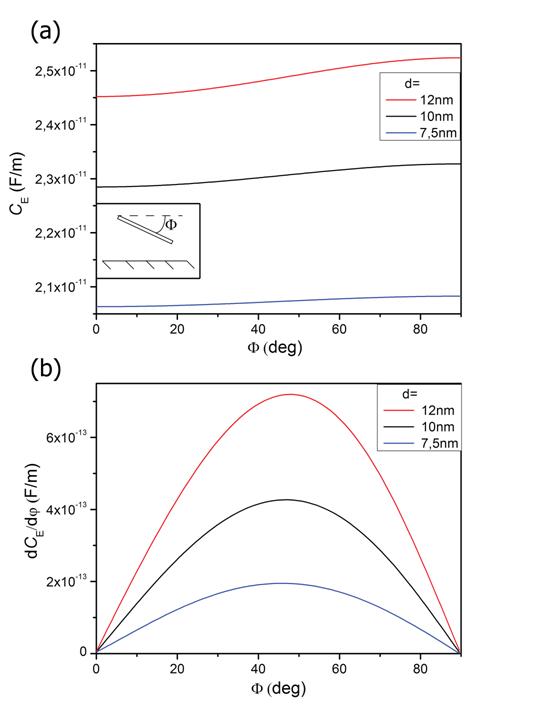
Рис. 4. Емкость системы (a) и производная емкости системы (b), как функции угла поворота графеновой наноленты.
Чувствительность устройства
Одним из основных параметров, определяющих качество детектирования рассматриваемым устройством, является чувствительность этого устройства. В данном случае чувствительность определяется как отношение амплитуды переменного тока выходного сигнала к мощности терагерцевого излучения, поглощаемого системой:
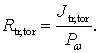 (10)
(10)
Здесь
![]() – амплитуда тока выходного сигнала на выходе
устройства в случае, соответственно, поперечных и крутильных колебаний.
Амплитуда наведенного тока зависит от амплитуды механических колебаний:
– амплитуда тока выходного сигнала на выходе
устройства в случае, соответственно, поперечных и крутильных колебаний.
Амплитуда наведенного тока зависит от амплитуды механических колебаний:
![]() и
и 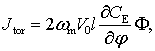 (11)
(11)
где ![]() –
базовое напряжение.
–
базовое напряжение.
Мощность излучения, поглощаемая системой, равна:
![]() (12)
(12)
где ![]() –
коэффициент усиления антенны,
–
коэффициент усиления антенны, ![]() –
скорость света в вакууме и
–
скорость света в вакууме и ![]() –
диэлектрическая постоянная.
–
диэлектрическая постоянная.
Таким образом, можно записать чувствительность детектора как
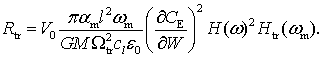 (13)
(13)
Аналогичное выражение может быть получено и для чувствительности детектора, основанного на крутильных колебаниях ГНЛ.
Для типичных размеров
системы и параметров ![]() ,
, ![]() ,
, ![]() оценки по полученным формулам дают
следующие величины:
оценки по полученным формулам дают
следующие величины:
![]() (14)
(14)
Полученные значения чувствительности детектора значительно превышают аналогичные значения этих параметров для детекторов такого типа на основе двумерного электронного газа [1-8], и приблизительно соответствуют значениям чувствительности детектора на основе углеродных нанотрубок [9].
Кроме рассмотренной схемы детектора на одной ГНЛ можно предложить также схему детектора на двух нанолентах (рис. 5а) и на массиве ГНЛ, расположенных над проводящей поверхностью (рис. 5b). В случае детектора на массиве ГНЛ следует ожидать, что его чувствительность будет пропорциональна количеству нанолент.

Рис. 5. Схематичное изображение терагерцевого детектора, основанного на двух ГНЛ (a) и массиве ГНЛ (b).
Заключение
В заключение перечислим основные результаты, полученные в настоящей работе. Предложен и теоретически обоснован новый вид наноразмерного резонансного детектора модулированного излучения терагерцевого диапазона на основе ГНЛ. Физическую основу предложенного детектора составляет возбуждение двойного резонанса: резонанса в механическом резонаторе на частоте модуляции и резонанса в плазменном резонаторе на несущей частоте. Принципиально, что, как было показано в настоящем исследовании, достаточно короткая ГНЛ представляет собой одновременно не только механический, но и, при определённых условиях, плазменный резонатор.
В основу описания электродинамики ГНЛ положена модель жидкости Томонаги-Латтинжера. Согласно этой модели, распространение электромагнитных волн (плазмонов) в ГНЛ описывается известной системой уравнений для передающей линии (телеграфными уравнениями), в которую дополнительно к классическим погонным емкости, индуктивности и сопротивлению следует ввести погонные квантовую емкость и кинетическую индуктивность. Последние величины зависят от квантовых параметров – скорости Ферми и квантового сопротивления. Кроме того, эти величины существенно зависят от числа каналов, или числа подзон размерного квантования, которое для рассматриваемых ГНЛ считается равным 4 (с учётом спина электронов). Скорость распространения плазменных волн в таких квантовых системах может быть почти на два порядка меньше, чем скорость света, что и обуславливает существование плазменных резонансов в терагерцевом диапазоне при таких малых по сравнению с длиной волны в вакууме (порядка 300 мкм) продольных размерах плазменного резонатора (порядка 1 мкм).
В рамках модели Томонаги – Латтинжера для электродинамического осциллятора и точечной модели для механического осциллятора проведен расчёт основных параметров и определена эффективность системы из одной ГНЛ, расположенной параллельно проводящей плоскости, как детектора модулированного терагерцевого излучения. Одним из важных теоретических результатов нам представляется выведенная в рамках принятых моделей универсальная формула для определения чувствительности любых детекторов, использующих описанный выше двойной резонанс, и любые виды механических и плазменных резонаторов.
Основная трудность в реализации предложенной схемы детектора заключается в оптимизации плазменного резонатора. Из-за рассеяния плазмонов в ГНЛ и больших значений контактных сопротивлений добротность плазмонных резонаторов не может быть достаточно большой. Однако потери в ГНЛ могут быть сведены к достаточно малой величине за счёт обеспечения баллистического режима движения носителей, что достигается при уменьшении длины ГНЛ до значений, существенно меньших длины свободного пробега носителей. Контактные сопротивления складываются из принципиально неустранимого квантового сопротивления и сопротивления макроскопических контактов, которое, согласно последним литературным данным, может быть уменьшено до значений, меньших квантовых. Влияние квантовых сопротивлений на добротность может быть уменьшено за счёт увеличения числа квантовых каналов и перехода к многослойным ГНЛ. По-видимому, наиболее радикальным методом повышения добротности является переход к индукционному способу активации таких резонаторов, при котором контактные и квантовые сопротивления не входят в эквивалентную электрическую схему резонатора.
Работа выполнена при частичной финансовой поддержке Министерства образования и науки Российской Федерации в рамках ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы» (контракт № 16.513.11.3129).
Литература
1. P.H. Siegel, Terahertz Technology, IEEE Trans. on Microwave Theory and Techniques, vol. 50, pp. 910-927, March 2002.
2. M. Tonouchi, Cutting-edge terahertz technology, Nat. Photonics, vol. 1, pp. 97-105, February 2007.
3. J. Federici and L. Moeller, Review of terahertz and subterahertz wireless communications, J. Appl. Phys., vol. 107, 111101, 2010.
4. V. Ryzhii, M. Ryzhii, Y. Hu, I. Hagiwara, and M.S. Shur, Resonant detection of modulated terahertz radiation in micromachined high-electron-mobility transistor, Appl. Phys. Lett., vol. 90, 203503, May 2007.
5. Y. Hu, M. Ryzhii, I. Hagiwara, M.S. Shur and V. Ryzhii, Combined resonance and resonant detection of modulated terahertz radiation in a micromachined high-electron mobility transistor, Phys. Stat. Sol. C., vol. 5, pp. 277-281, 2008.
6. V.G. Leiman, M. Ryzhii, A. Satou, N. Ryabova, V. Ryzhii, T. Otsuji, and M.S. Shur, Analysis of resonant detection of terahertz radiation in high-electron mobility transistor with a nanostring/carbon nanotube as the mechanically floating gate, J. Appl. Phys., vol. 104, 024514, 2008.
7. A.V. Arsenin, A.D. Gladun, V.G. Leiman, V.L. Semenenko and V.I. Ryzhii, Parametric instability in a nanoelectromechanical detector of modulated terahertz radiation on the basis of a high electron mobility transistor with a mobile elastic gate, J. Commun. Technol. Electron., vol. 54, pp. 1322-1330, 2009.
8. A.V. Arsenin, A.D. Gladun, V.G. Leiman, V.L. Semenenko and V.I. Ryzhii, Plasma oscillations of the two-dimensional electron gas in the field-effect transistor with a cylindrical gate electrode, J. Commun. Technol. Electron., vol. 55, pp. 1285-1294, 2010.
9. Yu. Stebunov, V. Leiman, A. Arsenin, A. Gladun, V. Semenenko, V. Ryzhii, Detection of Modulated Terahertz Radiation Using Combined Plasma and Mechanical Resonances in Double-Carbon-Nanotube Device, Appl. Phys. Express, vol. 4, 075101, 2011.
10. H.C. Nathanson, W.E. Newell, R.A. Wickstrom, J.R. Davis, The resonant gate transistor, IEEE trans. on Electron Devices, vol. 14, pp. 117-133, March 1967.
11. L. Ju, B. Geng, J. Horng, C. Girit, M. Martin, Z. Hao, H.A. Bechtel, X. Liang, A. Zettl, Y.R. Shen, F. Wang, Graphene plasmonics for tunable terahertz metamaterials, Nat. Nanotechnology, vol. 6, pp. 630-634, 2011.
12. X. Wang, Y. Ouyang, L. Jiao, H. Wang, L. Xie, J Wu, J. Guo, H Dai, Graphene nanoribbons with smooth edges behave as quantum wires, Nat. Nanotechnology, vol. 6, pp. 563-567, 2011.
13. T. Giamarchi, Quantum Physics in One Dimension. Oxford: Oxford University Press, 2003.
14. P.J. Burke, Luttinger Liquid Theory as a Model of the GHz Electrical Properties of Carbon Nanotubes, IEEE Transactions on Nanotechnology, vol. 1, pp. 129-144, 2002.
15. C. Rutherglen, P.J. Burke, Nano-Electromagnetics: Circuit and Electromagnetic Properties of Carbon Nanotubes, Small, vol. 5, pp. 884-906, 2009.
16. K. Eom, H.S. Park, D.S. Yoon, T. Kwon, Nanomechanical resonators and their applications in biological/chemical detection: Nanomechanics principles, Phys. Rep., vol. 503, pp. 115-163, 2011.
17. J.S. Bunch, A.M. van der Zande, S.S. Verbridge, I.W. Frank, D.M. Tanenbaum, J.M. Parpia, H.G. Craighead and P.L. McEuen, Electromechanical Resonators from Graphene Sheets, Science, vol. 26, pp. 490-493, January 2007.
18. D. Garcia-Sanchez, A.M. van der Zande, A. San Paulo, B. Lassagne, P.L. McEuen, and A. Bachtold, Imaging Mechanical Vibrations in Suspended Graphene Sheets, Nano Lett., vol. 8, pp. 1399-1403, 2008.
19. J.T. Robinson, M. Zalalutdinov, J.W. Baldwin, E.S. Snow, Z. Wei, P. Sheehan, and B.H. Houston, Wafer-scale Reduced Graphene Oxide Films for Nanomechanical Devices, Nano Lett., vol. 8, pp. 3441-3445, 2008
20. Y. Xu, C. Chen, V.V. Deshpande, F.A. DiRenno, A. Gondarenko, D.B. Heinz, S. Liu, P. Kim, and J. Hone, Radio frequency electrical transduction of graphene mechanical resonators, Appl. Phys. Lett., vol. 97, 243111, 2010.
21. B.D. Urso, M.V. Gurudev Dutt, S. Dhingra, and N.M. Nusran, Quantum measurements between a single spin and a torsional nanomechanical resonator, New J. of Phys., vol. 13, 045002, 2011.
22. S. Kitipornchai, X.Q. He, and K.M. Liew, Continuum model for the vibration of multilayered graphene sheets, Phys. Rev. B, vol. 72, 075443, 2005.
23. A. Sakhaee-Pour, M.T. Ahmadian, and R Naghdabadi, Vibrational analysis of single-layered graphene sheets, Nanotech., vol. 19, 085702, 2008.
24. S.Y. Kim and H.S. Park, The Importance of Edge Effects on the Intrinsic Loss Mechanisms of Graphene Nanoresonators, Nano Lett., vol. 9, pp. 969-974, 2009.
25. R. Chowdhury, S. Adhikari, F. Scarpa, and M.I. Friswell, Transverse vibration of single-layer graphene sheets, J. Phys. D: Appl. Phys., vol. 44, 205401, 2011.
26. R. E. Collin: Foundations for Microwave Engineering, Wiley, New York, 2nd ed, 2000.
27. C. Lee, X. Wei, J.W. Kysar, J. Hone, Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene, Science, vol. 321, pp. 385-388, 2008.
28. L.D. Landau and E.M. Lifshitz, Theory of Elasticity, Pergamon, New York, 1986.