Система компьютерной реконструкции 3D-распределений нейронов на основе априорной морфологической информации и серий изображений 2D-срезов головного мозга.

УДК 57.012.3; 57.081.23; 616.8

Система компьютерной реконструкции 3D-распределений нейронов на основе априорной морфологической информации и серий изображений 2D-срезов головного мозга

Ю. В. Обухов, В. Е. Анциперов, О. В. Евсеев

Институт радиотехники и электроники им. В. А. Котельникова РАН

Получена 23 июля 2012 г.

Аннотация. Изложены результаты разработки алгоритмов реконструкции пространственных трехмерных распределений нейронов, предварительно распознанных по микроскопическим изображениям срезов головного мозга экспериментальных животных. Рассмотрена адаптация с учетом сложившихся сегодня нейробиологических представлений известного EM-алгоритма кластеризации для выделения в срезах групп нейронов. Предложена полиномиальная межслойная аппроксимация параметров двумерных контуров групп, с помощью которой удается, как минимум, вдвое уменьшить количество срезов для трехмерной реконструкции плотности нейронов. Данные алгоритмы реализованы в разрабатываемом авторами программном комплексе построения 3D-распределений нейронов по серии изображений 2D-срезов головного мозга, который, как предполагается, станет удобным инструментом исследований в современной нейронауке, в частности, при моделировании болезни Паркинсона и позволит существенно снизить расходы на их проведения.

Ключевые слова: 3D реконструкция распределений, 2D кластеризация, EM-алгоритм, B-сплайны.

Abstract. The paper presents results of the development of reconstruction algorithms of three-dimensional distributions of neurons, previously recognized by microscopic images of brain slices of experimental animals. The adaptation of the well-known EM-clustering algorithm to highlight groups of neurons in slices is considered, taking into account the prevailing today neurobiological concepts. Authors propose a polynomial interlayer approximation of the parameters of two-dimensional contours of groups. It provides reduce at least halve the number of slices for the three-dimensional reconstruction of neuronal distributions. Described algorithms are implemented in a software package developed by the authors for constructing neuronal 3D-distributions on a series of 2D-slice images of the brain. It is supposed to be a useful tool for research in present neuroscience, in particular, for problems of the modeling of Parkinson's disease, and will significantly reduce the costs of such researches.

Keywords: 3D distributions reconstruction, 2D clustering, EM-algorithm, B-splines.

По данным доклада Всемирной организации здравоохранения (ВОЗ), неврологическими нарушениями страдает около одного миллиарда человек во всем мире [1]. При этом большой интерес вызывают нейродегенеративные заболевания, связанные с гибелью нейронов. К ним относятся болезни Паркинсона и Альцгеймера, рассеянный склероз и др., которые десятилетиями развиваются в скрытой форме и нередко проявляются на пике профессиональной и социальной активности человека. Несмотря на то, что лечить больных начинают сразу после появления симптомов, заболевания быстро прогрессируют, приводя к инвалидизации и летальному исходу.

Поэтому одной из важнейших задач нейронаук является разработка экспериментальных моделей социально-значимых заболеваний, в частности, связанных с гибелью нейронов, в том числе, в определенной части головного мозга – черной субстанции (ЧС), что приводит к развитию болезни Паркинсона (БП) [2]. Такие модели предназначены для разработки новых методов и технологий диагностики и лечения подобных заболеваний. Характерной особенностью БП является то, что она развивается в течение длительного времени (нескольких лет) в скрытой форме – без проявления симптомов, т.е. в «доклинической» стадии. Только после потери «порогового» числа нейронов черной субстанции (≈ 70%) начинают проявляться характерные симптомы – нарушение моторики, и заболевание переходит в клиническую стадию.

Предполагается, что по мере гибели нейронов в ЧС включаются механизмы пластичности мозга, способствующие компенсации функциональной недостаточности погибших нейронов. Детальное изучение данных компенсаторных процессов с целью управления ими направлено на разработку новых способов лечения БП.

Испытаниям методов диагностики и лечения должны предшествовать разработка и апробация этих технологий на адекватных экспериментальных моделях заболеваний, созданных на животных с использованием широкого спектра современных подходов. Разрабатываемые в Институте биологии развития им. Н.К.Кольцова РАН модели различных стадий БП, предполагают определение количества выживших нейронов и анализ их функционального состояния при различных схемах применения нейротоксина, с помощью которого моделируется БП. Отсутствие автоматизации данного процесса делает экспериментальное моделирование БП чрезмерно трудоемким и дорогостоящим. Один высококвалифицированный специалист в состоянии осуществить обработку материала от одного животного по следующим этапам:

1. приготовление замороженных срезов;

2. иммуноцитохимическое выявление дофаминергических нейронов и их аксонов по содержащемуся в них ключевому ферменту синтеза дофамина – тирозингидроксилазе и приготовление микроскопических препаратов;

3. перенос изображений тел нейронов и их аксонов в память компьютера, обведение вручную границ аксонов и тел нейронов, а также подсчет их количества, исчисляемого тысячами.

Для получения достоверных с биологической точки зрения результатов вышеописанные действия необходимо провести на большом количестве животных. Помимо высокой трудоемкости, работа требует больших материальных затрат на оборудование и реактивы. За счет автоматизации и оптимизации процедуры обработки и анализа экспериментальных данных отработка моделей БП могла бы продвигаться гораздо быстрее и была бы экономически эффективнее при снижении временных и материальных затрат на исследования.

В качестве источника экспериментальных данных для построения модели БП используются цифровые микроскопические изображения нейронов (МИН) и волокон срезов головного мозга экспериментальных животных (разрешение 0.0117 мкм²/пиксел²). Выжившие нейроны на фотографиях представляют собой темные округлые клетки со светлым ядром и выявляются на фронтальных серийных срезах компактной части чёрной субстанции (KЧС) толщиной 20 мкм (см. рис. 1). Они являются ключевым звеном регуляции моторного поведения. Прогрессирующая дегенерация нейронов приводит к развитию БП.

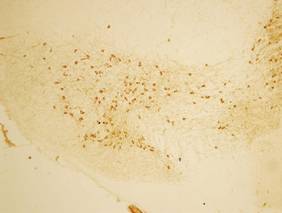
Описание: Описание: initial_image

Рис. 1. Изображение среза КЧС с химически выделенными нейронами

Автоматизация анализа МИН и отростков нейронов позволяет снизить материальные затраты на порядок, а временные затраты на два порядка [3]. Однако помимо задач распознавания нейронов на каждом изображении срезов ЧС встает задача упрощения анализа характера распределения нейронов по всему объему черной субстанции.

Наша работа посвящена созданию программно-алгоритмического обеспечения визуализации трехмерных распределений нейронов по двумерным данным [4], извлекаемым из цифровых изображений срезов ЧС с помощью систем автоматического распознавания [5].

В процессе проектирования системы реконструкции 3D-распределений нейронов на основе модели БП и серий изображений 2D-срезов мозга было выяснено, что ее функционирование должно осуществляться в виде цикла (конвейера) последовательных шагов. Такими шагами должны являться следующие:

1. выравнивание слоев – выделение на изображениях срезов согласованных между собой областей анализа и введение локальных (2D) координатных систем срезов, удобным образом связанных с выделенными областями, определение глобальной трехмерной (3D) системы координат и соотнесение с ней локальных координат всех срезов;

2. выделение нейронов – редактирование и согласование по срезам данных автоматического распознавания нейронов, определение их локальных координат, пересчет локальных 2D координат к 3D глобальным с целью последующей 3D визуализации самих нейронов;

3. кластеризация нейронов – построение двумерных непрерывных распределений плотности нейронов в срезах на основе нейробиологической модели БП и аппроксимации распределений моделями гауссовых смесей, известной как задача кластеризации;

4. выравнивание кластеров – определение типов кластеров и выравнивание их в соседних слоях по типу и затем по положению с целью получения плавных и соответствующих модели БП трехмерных объектов – 3D поверхностей постоянного уровня распределений плотности нейронов;

5. 3D-реконструкция распределений плотности нейронов по объему ЧС на основе аппроксимации поверхностей постоянного уровня сплайнами для межслойной интерполяции данных.

Основным этапом, требующим детальной теоретической и практической проработки, является создание алгоритмов кластеризации и 3D-реконструкции.

Черная субстанция расположена в среднем и промежуточном мозгу и образована серым веществом, имеет форму полосы, более широкой в средней части и суживающейся по концам, она изогнута с вогнутостью, направленной назад. Поскольку обе части ЧС в поперечном сечении – в плоскости срезов – представляют собой часть овала, предлагается разумным выделять их областью интересов (анализа) с эллиптической границей, нижняя часть которой проходит по нижней границе коры. В описанной области анализа располагаются интересующие нас нейроны, которые имеют тенденцию к группированию.

Модельно распределения нейронов принято представлять в виде некоторых скоплений – кластеров, причем основными интересующими специалистов характеристиками кластеров являются количество содержащихся в них нейронов и пространственное расположение самих кластеров.

Выделяемые на срезах специалистами «вручную» кластеры имеют, как правило, достаточно простую форму – это выпуклые области приблизительно овальной формы, могут быть достаточно вытянутыми в некотором направлении, как правило, не пересекают друг друга. Аппроксимация границ областей кластеров регулярными эллиптическими кривыми, вопросов у специалистов не вызывает. К примеру, на рис. 2 приведена разметка кластеров на некотором срезе сделанная нейробиологом и рядом приведена аппроксимация этих же областей эллиптическими кривыми. Видно, что не происходит потери информации при переходе на формализованную разметку, что подтверждают и специалисты.

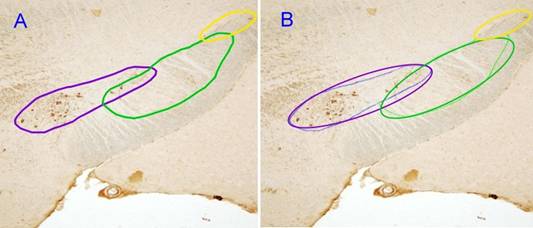
Рис. 2. Разметка кластеров (ИБР РАН, ИРЭ РАН) нейронов на срезе ЧС:

A) разметка кластеров на срезе сделанная нейробиологом вручную;

B) аппроксимация этих же кластеров регулярными (эллиптическими) кривыми.

Возможность задавать кластеры эллиптическими областями имеет огромные преимущества:

1. Общая эллиптическая кривая задается достаточно простым математическим выражением (a и b – полуоси, φ – угол наклона):

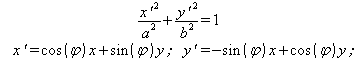
поэтому ее легко задавать и производить с ней вычисления.

2. В полярных координатах эллиптическая кривая задается формулой:

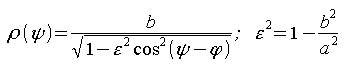
что позволяет почти равномерно распределить точки по кривой (для ψ=2π/k) и отобразить их на цифровом экране.

3. Квадратичная форма в экспоненте Гауссова распределения:

где

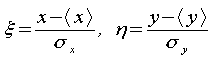
при фиксированном ее значении задает эллипс, что позволяет рассматривать последний как линию постоянного значения (уровня) распределения.

Последнее замечание позволяет трактовать эллиптические кластеры как уровни распределений известных в статистике как гауссовы смеси, а задачу кластеризации – как задачу нахождения параметрического распределения вероятностей, наилучшим образом описывающего дискретные экспериментальные данные (координаты нейронов).

К счастью, на сегодняшний день известны хорошие алгоритмы решения приведенной выше формализованной задачи. Одним из таких широко известных алгоритмов, позволяющих эффективно работать с большими объемами данных, является EM-алгоритм [6]. Его название происходит от слов «expectation-maximization», что переводится как «ожидание-максимизация». Это связано с тем, что каждая итерация содержит два шага – вычисление математических ожиданий (expectation) и максимизацию (maximisation). Перейдем к изложению адаптированной к данному проекту версии EM-алгоритма.

В основе идеи EM-алгоритма лежит предположение, что исследуемое множество данных может быть смоделировано с помощью линейной комбинации двумерных нормальных распределений (гауссовых смесей), а целью является оценка параметров, которые максимизируют логарифмическую функцию правдоподобия, используемую в качестве меры качества модели. Иными словами, предполагается, что данные в каждом кластере подчиняются определенному закону распределения, а именно, нормальному распределению (рис. 3). С учетом этого предположения можно определить параметры – математическое ожидание и дисперсию, которые соответствуют закону распределения элементов в кластере, наилучшим образом «подходящему» к наблюдаемым данным.

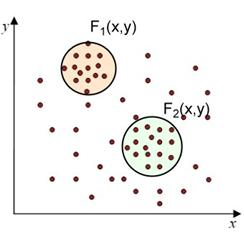
Рис. 3. Распределение элементов в кластерах

Таким образом, мы предполагаем, что любое наблюдение принадлежит ко всем кластерам, но с разной вероятностью. Тогда задача будет заключаться в «подгонке» распределений смеси к данным, а затем в определении вероятностей принадлежности наблюдения к каждому кластеру. Очевидно, что наблюдение должно быть отнесено к тому кластеру, для которого данная вероятность выше.

Среди преимуществ EM-алгоритма можно выделить следующие:

- Надежная статистическая основа.

- Линейное увеличение сложности при росте объема данных.

- Устойчивость к шумам и пропускам в данных.

- Возможность построения желаемого числа кластеров.

- Быстрая сходимость при удачной инициализации.

Однако алгоритм имеет и ряд недостатков. В частности, при неудачной инициализации сходимость алгоритма может оказаться медленной. Кроме этого, алгоритм может остановиться в локальном минимуме и дать квазиоптимальное решение.

Как отмечалось выше, EM-алгоритм предполагает, что кластеризуемые данные подчиняются линейной комбинации (смеси) нормальных (гауссовых) распределений, плотность вероятности которых имеет вид:

где – математическое ожидания, – дисперсия, – коэффициент корреляции.

Введем в рассмотрение функцию , которую будем рассматривать как обобщенное расстояние от до .

Алгоритм предполагает, что данные подчиняются смеси двумерных нормальных распределений. Модель, представляющая собой смесь гауссовых распределений задается в виде:

где – нормальное распределение для i-го кластера, доля (вес) i-го кластера в гауссовой смеси.

Существуют два подхода к решению задач кластеризации: основанный на расстоянии и основанный на плотности. Первый подход заключается в определении областей пространства признаков, внутри которых точки данных расположены ближе друг к другу, чем к точкам других областей, относительно некоторой функции расстояния (например, обобщенной). Второй – обнаруживает области, которые являются более «заселенными», чем другие. Алгоритмы кластеризации могут работать сверху вниз (дивизимные) и снизу вверх (агломеративные). Агломеративные алгоритмы, как правило, являются более точными, хотя и работают медленнее.

Используемый нами EM-алгоритм основан на вычислении расстояний. Он может рассматриваться как обобщение кластеризации на основе анализа смеси вероятностных распределений. В процессе работы алгоритма происходит итеративное улучшение решения, а остановка осуществляется в момент, когда достигается требуемый уровень точности модели. Мерой в данном случае является монотонно увеличивающаяся статистическая величина, называемая логарифмическим правдоподобием L:

Целью алгоритма является оценка средних значений , параметров и и весов смеси для функции распределения вероятности описанной выше таких, что они доставляют максимум функции правдоподобием L (принцип максимума правдоподобия – МП) при заданном наборе координат нейронов i=1,2, …, n).

Помимо введенных выше параметров введем еще так называемые «скрытые» параметры – апостериорные вероятности принадлежности i‑му кластеру. Рекуррентная максимизация функции правдоподобия L на основе EM алгоритма осуществляется по следующей принципиальной схеме:

шаг E: по формуле Байеса уточняются (оцениваются) «скрытые» параметры :

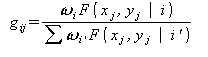
шаг M: с использованием уточняются параметры , , , (на самом деле приведенные ниже оценки максимизируют L при заданных ):

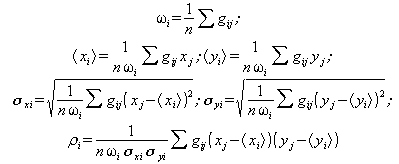
При рассчитанных параметрах принадлежность i-му кластеру определяется в соответствии с: . Итерации E-M продолжаются до тех пор, пока принадлежность кластерам не перестанет изменяться.

Решение задачи в данной общей постановке сложно даже для ее численной реализации. Поэтому часто прибегают к некоторым ограничениям упрощающим решение [7]. Так, в алгоритме кластеризации k-means все всегда полагаются равными , также равными и , а и оптимизация осуществляется только по положениям кластеров . При этом алгоритм кластеризации k-means осуществляется по следующей принципиальной схеме:

шаг E: «скрытые» параметры уточняются (оцениваются) по формуле:

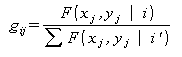
шаг M: уточняются параметры :

Отметим, что принадлежность i-му кластеру определяется в k-means по минимуму – евклидова расстояния до – центра i-го кластера.

В случае, когда кластеры пересекаются слабо, также можно упростить EM алгоритм даже в общем его виде, если учесть, что при этом все распределения очень малы в сравнении с тем , к центру которого ближе всего . При этом адаптированный алгоритм кластеризации осуществляется по следующей схеме:

шаг E: «скрытые» параметры уточняются (оцениваются) по формуле:

шаг M: уточняются параметры , , при , – число нейронов, для которых (число нейронов, для которых центр i-го кластера – ближайший):

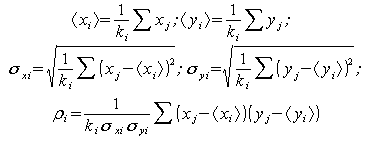
причем суммирование в приведенных формулах идет только по нейронам кластера ().

Алгоритм начинает работу с инициализации, т.е. некоторого начального числа кластеров и некоторого приближенного решения, которое может быть выбрано случайно или задано пользователем исходя из некоторых априорных сведений об исходных данных (например, на основе обобщенной модели Паркинсона). Наиболее общим способом инициализации является присвоение элементам математических ожиданий некоторых априорных значений, а начальные , и задаются как в алгоритме k-means: , .

Для проверки работы адаптированного алгоритма EM нами было разработано небольшое приложение на MatLab, внешний вид интерфейсной формы которого приведен на рис. 4.

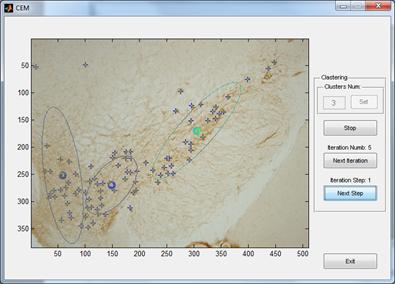
Рис. 4. Интерфейс экспериментального ПО CEM (MatLab) для проверки адаптированного алгоритма EM на реальных срезах ЧС.

Результаты тестирования CEM (MatLab) для проверки адаптированного алгоритма EM на реальных срезах ЧС показали замечательные его характеристики: при заданном количестве кластеров и при достаточно грубых априорных расположениях их центров распределение нейронов по кластерам устанавливается за 4-5 итераций и параметры кластеров и хорошо соответствуют ожидаемым значениям.

После кластеризации нейронов на каждом срезе необходимо провести очевидные шаги, связанные с выравниванием изображений друг относительно друга по некоторым абсолютным признакам (например, по границе коры), для последующего верного построения их трехмерных распределений в полном объеме черной субстанции.

Общая задача реконструкции 3D поверхностей постоянного уровня распределений нейронов на основе двумерных контуров – границ кластеров и содержащей их области анализа может решаться различными методами реконструкции, однако, ввиду сложности задачи в общей постановке, целесообразно использовать выявленную специфику проблемы для ее возможного упрощения. Спецификой задачи является тот факт, что все слои являются параллельными, а контуры могут быть формализованы до регулярных (эллиптических) кривых. Для таких слоев достаточно легко строится межслойная интерполяция также контурами эллиптической формы, например, при помощи сплайнов (интерполируются только шесть параметров: пять параметров задающих эллипс и шестой – макс. плотность).

В компьютерном моделировании сплайны – это степенные функции одного или двух переменных, графическими образами которых являются кривые линии или криволинейные поверхности [8]. Они служат, в частности, для решения задачи интерполяции, то есть нахождения промежуточных точек кривой линии или поверхности, заданной опорными точками. Уравнения сплайнов имеют, обычно, степень не выше третьей, так как именно такая степень является минимально необходимой для гладкой стыковки криволинейных участков. Покажем это на примере сплайн-функции одной переменной.

Пусть две точки Р₁ и Р₂, показанные на рис. 5, нужно соединить кривой S таким образом, чтобы она проходила через эти точки и гладко сопрягалась с соседними участками кривой. Соседние участки на рисунке показаны толстыми сплошными линиями, а желаемый вид кривой S – штриховой линией.

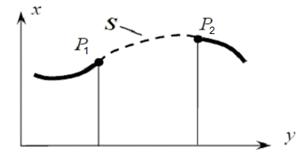
Рис. 5. Сплайн-интерполяция по двум точкам

Очевидно, для решения задачи нужно наложить на кривую S четыре ограничения:

1) и 2) – кривая проходит через точки Р₁ и Р₂, тогда составная кривая не будет иметь разрывов первого рода;

3) и 4) – сопряжение кривой S с соседними участками в точках Р₁ и Р₂ является плавным (гладким), тогда составная кривая не будет иметь разрывов второго рода.

Для этого требуется иметь математическое описание кривой S в виде многочлена, имеющего не менее четырех коэффициентов. Самым простым из таких многочленов является многочлен третьей степени, который, в общем случае, имеет вид:

y = ax³ + bx² + cx + d,

включающий как раз четыре коэффициента формы a, b, c и d. Тогда наложение четырех упомянутых ограничений дает систему четырех уравнений с четырьмя неизвестными:

1) прохождение через Р₁:

y₁ = ax₁³ + bx₁²+ cx₁ + d,

2) прохождение через Р₂:

y₂ = ax₂³ + bx₂²+ cx₂ + d,

3) равенство первых производных соседних сплайнов в точке Р₁:

y₁ = 3ax₁² + 2bx₁+ c,

4) равенство первых производных соседних сплайнов в точке Р₂:

y₂ = 3ax₂² + 2bx₂+ c.

Сплайновая поверхность, в отличие от кривой, должна проходить через четыре точки, являющиеся для нее угловыми. Поверхность можно представить как результат движения кубической кривой параллельно самой себе. При этом конечные точки этой кривой в процессе движения скользят по двум другим (боковым) кубическим кривым. В результате получается поверхность, которая описывается бикубическим степенным многочленом. Каждое слагаемое многочлена включает два аргумента, имеющих в различных сочетаниях степени от 0 до 3. Существует много разновидностей сплайновых поверхностей, обладающих различными свойствами и формируемых с использованием различных условий и геометрических параметров.

Для описания сплайнов можно использовать явную, неявную и параметрическую формы. В компьютерной графике обычно используют параметрическое описание сплайнов. Явная форма описания в декартовой системе координат по ряду причин используется редко. Во-первых, вид описания поверхности в явной форме зависит от выбранного положения системы координат. Во-вторых, некоторые участки поверхности могут иметь вертикальные касательные векторы, то есть стремящиеся к бесконечности производные. В этом случае невозможно задать условия стыковки сегментов поверхности. Наконец, в-третьих, параметрическое представление, в отличие от явной формы, описывает естественный последовательный обход участков поверхности в процессе ее развертывания во времени. В общем случае, сегмент сплайновой поверхности описывается бикубическими выражениями вида

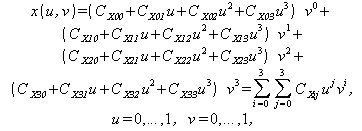(1)

где u и v – параметры описания (аргументы сплайн-функции), C_X₀₀, ... ,C_X₃₃– коэффициенты формы, определяющие геометрические характеристики поверхности.

Аналогичный вид имеют выражения y(u,v) и z(u,v), включающие наборы коэффициентов C_Y₀₀, ... , C_Y₃₃ и C_Z₀₀, ... , C_Z₃₃, соответственно.

Смысл выражения (1) следующий. Аргументы u и v представляют собой координаты криволинейной координатной системы, расположенной на поверхности сплайна. В ней каждая точка поверхности задается парой числовых значений. Для отображения поверхности координаты ее точек с помощью (1) переводятся в декартову систему координат, в которой расположена экранная плоскость. Соответствие координат текущей точки СР сплайновой поверхности в двух упомянутых координатных системах показано на рис. 6.

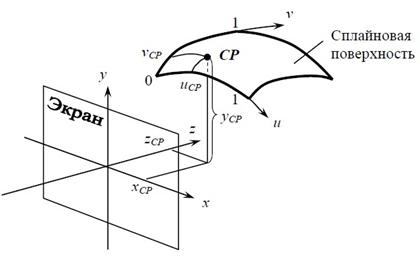
Рис. 6. Соответствие между параметрическими и декартовыми координатами

Коэффициенты многочленов отыскиваются при наложении ограничений на форму сегмента поверхности. В зависимости от выбора ограничений поверхность получает ту или иную форму описания. Например, ограничениями для поверхности Кунса (частный случай – поверхность Эрмита, поверхность Фергюсона) являются условия ее прохождения через заданные угловые точки, а также соответствие заданным значениям частных производных (то есть наклонов) в угловых точках поверхности и смешанных частных производных (то есть кручений) в этих точках. Использование таких ограничений является геометрически понятным, но сложно реализуемым. В компьютерных системах геометрического моделирования в качестве ограничений обычно используется повторение сплайном формы некоторой многогранной опорной поверхности (характеристического многогранника), заданной шестнадцатью опорными точками. Поверхность должна проходить вблизи опорных точек или через некоторые из них, и изменение их координат должно приводить к изменению формы поверхности. Поэтому описание сегмента поверхности представляют не в форме (1), а в другом виде, выражая коэффициенты многочленов через координаты опорных точек. Описание в координатной форме имеет вид

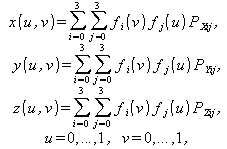
(2)

где P_X, P_Y, P_Z – массивы x, y и z – координат опорных точек, f_i(u), f_j(v) – функциональные коэффициенты, имеющие свой вид для каждой разновидности сплайн-функций.

Значения функций f_i(u), f_j(v) выступают как весовые коэффициенты координат опорных точек, поэтому эти функции называют весовыми или смешивающими.

В компьютерной графике обычно применяется описание сплайна в матричной форме, которое выглядит следующим образом:

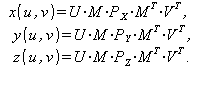(3)

где U и V – векторы степеней параметров u и v: U = | u³ u² u 1| и V = | v³ v² v 1|;

P_X, P_Y, P_Z геометрические матрицы, содержащие координаты x, y и z опорных точек,

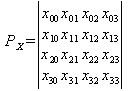M – базисная матрица поверхности, которая содержит числовые коэффициенты, определяющие своеобразие поверхности.

Сплайны характеризуются рядом полезных свойств. Было уже упомянуто, что форма сплайнового сегмента следует за формой характеристического многогранника. Если все его опорные точки лежат в одной плоскости, то все текущие точки сплайна тоже лежат в этой плоскости. Характеристический многогранник является описанным вокруг сплайновой поверхности, следовательно, попадание этой поверхности в некоторый объем (например, объем видимости наблюдателя) легко проверяется по шестнадцати точкам. Кроме того, сплайны инвариантны по отношению к аффинным преобразованиям. Это означает, что при необходимости сдвига, поворота, масштабирования и отражения сплайна не нужно подвергать этим преобразованиям все текущие точки сегмента. Достаточно выполнить преобразования только над опорными точками, а потом просто применить алгоритм развертывания сплайна по выражениям (3) на этих преобразованных опорных точках.

В компьютерной графике широко применяются базовые сплайны, или В-сплайны («би-сплайны») [9]. Их математическая модель в матричной форме также описывается выражениями (3). Форма В-сплайна однозначно задается координатами опорных точек, однако, сегмент, в общем случае, только приближается к опорным точкам и может не проходить ни через одну из них. Для В-сплайновой поверхности третьей степени функциональные коэффициенты в выражениях (2) определяются формулами:

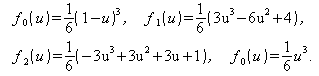(формулы для многочленов f_j(v) отличаются от приведенных только тем, что в них всюду вместо параметра u стоит параметр v), а базисная матрица M имеет вид:

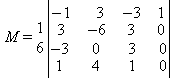Подставив матрицу М в выражения (3) и проделав необходимые матричные операции, можно убедиться, что В-сплайн не проходит через опорные точки. Например, текущая точка с параметрическими координатами u=v=0 получает следующее значение координаты х:

x(u,v) = (x₀₀+4x₁₀+x₂₀+4x₀₁+16x₁₁+4x₂₁+x₀₂+4x₁₂+x₂₂)/36

Оно показывает, что координата текущей точки не совпадает с координатой ни одной опорной точки, а является суммой вкладов, которые вносят несколько опорных точек. Наибольший вклад вносит опорная точка Р₁₁, следовательно, именно к ней и будет ближе текущая точка при нулевых значениях аргументов u и v.

Применение B-сплайнов упрощает процесс моделирования сложных поверхностей. Любые 16 характерных точек поверхности, образующие четырехугольник 4-4 точки, могут быть приняты за опорные точки В-сплайного примитива. При этом сформированный сегмент займет не весь характеристический многогранник, а расположится вблизи четырех средних точек Р₁₁, Р₁₂, Р₂₁, Р₂₂.

Необходимо отметить, что при моделировании участков поверхности с помощью В-сплайновых примитивов требуется обычно больше вычислений, чем для других сплайнов. Например, по сравнению со сплайнами Безье [10] требуется в девять раз больше вычислений. Однако, этот недостаток В-сплайнов компенсируется их повышенной гладкостью, достигаемой без введения дополнительных опорных точек.

Простая методика моделирования пространственных поверхностей сложной формы включает следующие шаги:

1) поверхность представляется набором принадлежащих ей характерных точек. Выбирается расположение координатных осей u и v. Характерные точки принимаются за опорные точки В-сплайновых примитивов;

2) образуется «окно» включающее 16 опорных точек (по 4 вдоль каждой координатной оси). По выражениям (3) происходит вычисление координат текущих точек примитива;

3) по окончании развертывания очередного примитива окно перемещается на один ряд опорных точек по оси u или v. В результате перемещения в окно входят 12 прежних опорных точек и 4 новые точки. Для этого набора опорных точек по выражениям (3) вычисляются координаты текущих точек;

4) пункт 3) выполняется до тех пор, пока не будут использованы все опорные точки. После этого выполняется визуальный контроль смоделированной поверхности. Для коррекции рельефа по результатам контроля изменяется положение опорных точек.

Привязка В-сплайнового сегмента к центральной части характеристического многогранника приводит к тому, что смоделированная поверхность не проходит через крайние (граничные) характерные точки исходной поверхности. Чтобы получить сегменты, примыкающие к границам поверхности нужно иметь дополнительные ряды опорных точек. Для решения задачи прибегают к так называемым кратным граничным опорным точкам. Кратными называются опорные точки, имеющие различные обозначения, но одинаковые координаты. Кратные опорные точки образуются повторением координат граничных опорных точек и присвоением новым точкам уникальных обозначений. Каждая граничная опорная точка получает одну дополнительную, кратную себе, а четыре угловые точки получают по три дополнительные опорные точки каждая.

При анализе проблемы реконструкции трехмерного распределения нейронов были исследованы методы построения поверхностей сплайнами или кривыми других полиномиальных типов в ситуации, близкой к нашей и было выявлено, что наиболее подходящим для реконструкции является так называемый лофтинг-метод [11].

Лофтинг-метод восстанавливает поверхность 3D-объекта неравномерными рациональными би-сплайнами, которые, в частности, хорошо аппроксимируют регулярные контуры объекта. Loft-объекты строятся путем формирования оболочки по опорным сечениям, расставляемым вдоль некоторой заданной траектории. Оболочка как бы натягивается на сечения вдоль указанного пути, а в результате получается трехмерная модель. Данный метод моделирования прекрасно подходит для тех моделей, форма которых может быть охарактеризована некоторым набором поперечных сечений, как в нашем случае. В основе любого подобного объекта всегда лежат траектория (путь) и одно или более сечений. Путь задает основную линию лофт-объекта и может иметь форму прямой, окружности, произвольной кривой и т.п., а сечения определяют его форму и тоже могут быть самыми разнообразными (в разумных пределах). При использовании нескольких сечений они размещаются вдоль пути по указанному пользователем принципу, а в случае одного сечения данная форма размещается на обоих концах пути. Оба типа структурных элементов – путь и сечения – в общем случае представлены обычными сплайнами, т.е. наборами опорных вершин. Число опорных вершин поперечных сечений может быть произвольным, но это число должно быть во всех задействованных в loft-объекте сечениях одинаково. Кроме того, если сечение представлено составными формами, то данные формы должны иметь одинаковый порядок вложения. Это означает, что если первое сечение содержит внутри одного контура два других контура, то и все последующие сечения должны быть сформированы по тому же принципу. А если в копии данной составной формы переместить два внутренних сплайна вне исходного, то ее уже нельзя будет указать в качестве второго сечения. Правда, при желании в ряде случаев данное ограничение можно обойти, превратив обычные замкнутые сплайны в разомкнутые. Форма лофт-объекта определяется не только за счет пути и определенного набора сечений – не менее важны положение внутренних сечений вдоль пути и согласование первых вершин каждой формы поперечного сечения. От размещения сечений вдоль пути зависит то, как и в какой момент будет смоделирован переход от одного сечения к другому, а согласование вершин позволяет избежать перекручивания моделей при переходе от сечения к сечению или, наоборот, при необходимости искусственно скручивать объекты. Качество лофтинг-метода сильно зависит от качества контуров, особенно в случае ручной обводки.

Другие технические проблемы создания лофт-объектов касаются плотности каркаса поверхности (или оболочки). Когда принимается решение о сложности loft-объекта необходимо сделать выбор из ряда компромиссов:

1. Плотные каркасы показывают большее число деталей, чем разреженные.

2. Плотные каркасы деформируются более однородно, чем разреженные.

3. Плотные каркасы визуализируются в более гладкий профиль, чем разреженные.

4. Разреженные каркасы используют меньше памяти и отображаются быстрее.

5. С разреженными каркасами, как правило, проще и быстрее работать, нежели с плотными.

Лучшее решение достигается путем создания как можно более разреженных каркасов, удовлетворяющих требованиям проекта по визуализации распределений. Впрочем, в программное обеспечение, предназначенное для визуализации распределений нейронов, при разработке закладывается возможность ручного выбора «гладкости» 3D объектов – плотности каркаса поверхности.

При формировании реконструкции 3D поверхностей постоянного уровня распределений нейронов при помощи лофт-объектов особое внимание должно быть уделено концам лофт-объектов и их конструкции (проблема создания наконечников). Каркасы границ кластеров должны представлять собой замкнутые поверхности и создавать визуальную иллюзию цельности.

Описанные выше алгоритмы используются в системе реконструкции трехмерного распределения нейронов по цифровым изображениям срезов ЧС. Заложенный в системе конвейер операций отражен в интерфейсе пользовательской программы – на форме представлен следующий набор вкладок: выравнивание слоев, выделение нейронов, кластеризация, выравнивание кластеров, 3D-представление (рис. 7). На каждой вкладке обеспечиваются средства ручного и автоматического редактирования для соответствующего шага процесса.

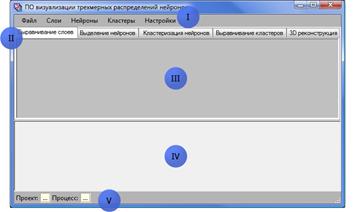
Рис. 7. Интерфейс разрабатываемого программного комплекса: главное меню (I); вкладки 5 шагов процесса реконструкции (II); панель вывода соответствующей графической информации (III); панель выбора среза (IV); строка состояния (V).

Со стороны программной реализации системы за каждым из шагов процесса реконструкции закреплен свой отдельный программный модуль, содержащий набор соответствующих данному шагу алгоритмов. Каждый из этих модулей имеет свои входные/выходные данные, хранящиеся в отдельных файлах БД проекта, и связан с соответствующей страницей интерфейса системы для редактирования входных и анализа выходных данных.

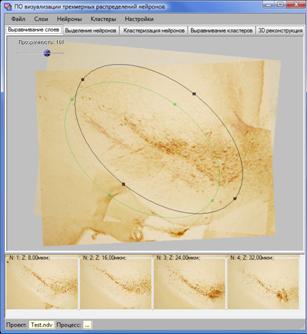
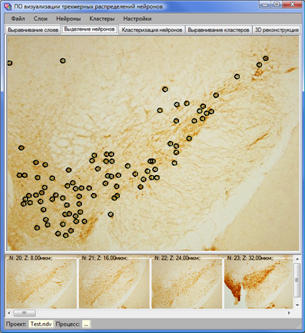
а) б)

Рис. 8. Интерфейс модулей а) «выравнивание слоев» и б) «выделение нейронов».

Модуль «выравнивание слоев» предназначен для выравнивания изображений соседних срезов (текущего относительно предыдущего) и выделения эллиптической области анализа (для текущего среза), с которой связывается система локальных координат данного среза (рис. 8а). Модуль «выделение нейронов» (рис. 8б) предназначен для редактирования координат нейронов, помеченных вручную или автоматически распознанных с помощью алгоритмов распознавания, разработанных соисполнителями по проекту ВЦ им. А.А.Дородницына РАН [5].

Вкладка «кластеризация» предназначена для автоматического выделения групп нейронов на срезах, используя адаптированный EM-алгоритм (рис. 9). С помощью модуля «выравнивание кластеров» согласовываются кластеры на соседних срезах по типам. Однако, перед согласованием необходимо каждому из кластеров приписать его уникальный на срезе тип. Эта процедура может быть осуществлена как вручную, так и автоматически по критерию ближнего по евклидову расстоянию кластера предыдущего слоя (если кластеры предыдущего слоя уже типизированы).

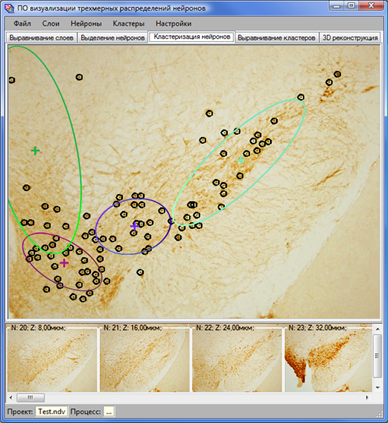
Рис. 9. Интерфейс модуля «кластеризация».

Последний шаг процесса непосредственно «3D-реконструкция» (рис. 10), на котором на основе плоских, параллельных контуров, как на формах lofting-объектов, строятся 3D-поверхности пространственных распределений. На этой вкладке пользователь осуществляет визуальный анализ рассчитанных распределений, представленных 3D-объектами. Средства DirectX-3D управления камерой предоставляют возможность быстро и просто реализовать такие функции анализа и визуализации 3D-модели, как изменение точки обзора, повороты, приближение к объекту или удаление от него и т.д.

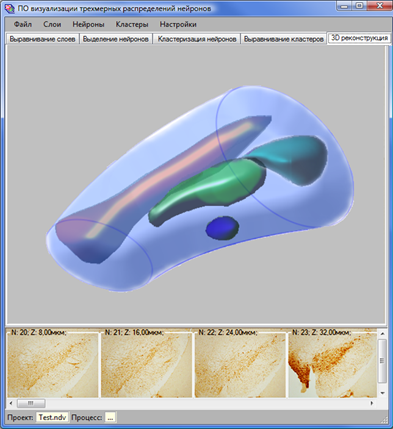
Рис. 10. Интерфейс модуля «3D-реконструкция».

Использования достижений современной математической теории в прикладных нейробиологических задачах позволяет осуществлять надежную и эффективную автоматизацию извлечения информации о нейронах из изображений срезов головного мозга и реконструкцию их трехмерного распределения, обеспечивая существенную экономию времени и материальных затрат на построение моделей нейродегенеративных заболеваний. И это в первую очередь связано с разработкой новых алгоритмических методов анализа данных и синтеза обобщенных способов их графического представления, с учетом сложившихся на сегодняшний день нейробиологических представлений.

По результатам работы над проектом к настоящему моменту:

- разработана методология реконструкции трехмерного распределения нейронов по данным их распознавания в изображениях серийных срезов головного мозга;

- адаптирован к задаче выделения контуров распределения нейронов в срезах алгоритм кластеризации, основанный на известном ЕМ-методе (оценивание-максимизация);

- разработана полиномиальная межслойная аппроксимация параметров двумерных контуров кластеров, с целью уменьшения количества срезов для трехмерной реконструкции плотности нейронов;

- разработано экспериментальное программное обеспечение ВТРН;

- в ПО включена возможность использования выходных данных программных комплексов автоматического распознавания нейронов по изображениям срезов мозга.

Работа финансово поддержана проектом «Разработка и исследование программно-алгоритмических методов автоматизации распознавания изображений нейронов и реконструкции их трехмерного распределения» федеральной целевой программы «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы», государственный контракт № 07.514.12.4029 [12].

Литература

1. По данным нового доклада ВОЗ, неврологическими нарушениями страдают миллионы людей во всем мире. Брюссель/Женева, 2007. [Электронный ресурс]. Режим доступа: http://www.who.int/mediacentre/news/releases/2007/pr04/ru/

2. R.L.Albin, А.В.Young, J.В.Penney. The functional anatomy of basal ganglia disorders. Trends Neurosci, 12. 1989. – pp. 366-75

3. I.Gurevich, V.Beloozerov, A.Myagkov, Yu.Sidorov, Yu.Trusova. Systems of Neuron Image Recognition for Solving Problems of Automated Diagnoses of Neurodegenerative Diseases. Pattern Recognition and Image Analysis: Advances in Mathematical Theory and Applications, 21(3). 2011. – pp. 392-397.

4. Обухов Ю.В., Анциперов В.Е. и др. Система распознавания нейронов и реконструкции их трехмерного распределения по цифровым изображения срезов черной субстанции и стриатума мозга экспериментальных животных. Сборник тезисов всероссийской конференции «Проведение научных исследований в области обработки, хранения и защиты информации». Москва, 2011. – С. 97-99.

5. I.B.Gurevich, E.A.Kozina, A.A.Myagkov, M.V.Ugryumov, V.V.Yashina. Automating Extraction and Analysis of Dopaminergic Axon Terminals in Images of Frontal Slices of the Striatum. Pattern Recognition and Image Analysis: Advances in Mathematical Theory and Applications, 20(3). 2010. – pp. 349-359.

6. Neal, Radford; Hinton, Geoffrey (1999). Michael I. Jordan. A view of the EM algorithm that justifies incremental, sparse, and other variants. Learning in Graphical Models (Cambridge, MA: MIT Press). 1999. – pp. 355–368.

7. Мандель И. Д. Кластерный анализ. М.: Финансы и Статистика, 1988. С. 98‑117.

8. Fan, Jianqing & Yao, Qiwei (2005). Spline Methods. Nonlinear time series: nonparametric and parametric methods. Springer. p. 246, 2005.

9. Эдвард Эйнджел. Интерактивная компьютерная графика. Вводный курс на базе OpenGL, 2-е изд. – С. 438‑445.

10. Роджерс Д., Адамс Дж. Математические основы машинной графики. М.: Мир, 2001. – С. 296-310.

11. H. Park. An Approximate Lofting Approach for B-Spline Surface Fitting to Functional Surfaces. The International Journal of Advanced Manufacturing Technology. Volume 18, Number 7 (2001), pp. 474-482.

12. Открытые конкурсы Минобрнауки России на размещение заказов, информация о лоте, 2011. [Электронный ресурс]. Режим доступа: http://contests-mon.informika.ru/lot/8509/