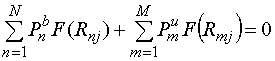УДК 621.396.67
О ФОРМИРОВАНИИ ОБЛАСТЕЙ С МАЛЫМ ЗНАЧЕНИЕМ ЭЛЕКТРИЧЕСКОГО ПОЛЯ НА КОНЕЧНОМ РАССТОЯНИИ ОТ СИСТЕМЫ ИЗЛУЧАТЕЛЕЙ
В. А. Пермяков, А. Н. Корюкин, М. С. Михайлов, Д. В. Сороковик
Национальный исследовательский университет «МЭИ»
Получена 1 июля 2013 г.
Аннотация. Поставлена задача формирования неподвижных нулей электрического поля на конечном расстоянии от системы излучателей. Рассмотрена система параллельных электрических вибраторов. Параметры части вибраторов используются для формирования диаграммы направленности, параметры остальных вибраторов – для формирования нулей электрического поля. Подход представляет практический интерес при создании антенных систем, обеспечивающих минимальное значение электрического (магнитного) поля на конечном расстоянии от излучателей.
Ключевые слова: Система параллельных линейных вибраторов, нули электрического (магнитного) поля, ближняя, промежуточная зоны.
Abstract. The problem of formation of stationary zeros of the electric field at a finite distance from a system of radiators is posed. A system of parallel electric dipoles is considered. Parameters of some dipoles are used for formation of the radiation pattern and parameters of remaining dipoles, for formation of zeros of the electric field. This approach is of practical interest for the development of antenna systems ensuring the minimum value of the electric (magnetic) field at a finite distance from radiators.
Key words. System of parallel linear dipoles, zeros of the electric (magnetic) field, near and transition zones.
Введение
В инженерной практике широко используются методы управления положением нулей диаграммы направленности (ДН) антенн, основанные на решении задачи синтеза нулей ДН. Мы предлагаем рассмотреть более общую задачу синтеза нулей электрического (магнитного) поля антенны, расположенных на конечном расстоянии от антенны в любой (ближней, промежуточной, дальней) зоне антенны. С физической точки зрения в переменном электромагнитном поле излучающих систем следует различать движущиеся нули электрического и магнитного полей, и неподвижные нули, возникающие вследствие интерференции бегущих волн. С формальной точки зрения в трехмерном пространстве неподвижные нули электрического (магнитного) поля могут формироваться в точках, на линиях или на поверхностях.
В дальней зоне нет различий между положениями нулей электрического и магнитного полей вследствие того, что электромагнитное поле в дальней зоне всегда имеет локальную структуру Т волны и компоненты электрического и магнитного полей жестко связаны через импеданс свободного пространства. В промежуточной и ближней зонах излучателя нули электрического и магнитного полей разделяются в пространстве, причем тем сильнее, чем ближе к излучателю. Таким образом, могут быть поставлены задачи синтеза нулей отдельно электрического или магнитного поля, или нулей электрического и магнитного полей вместе.
Следует отметить, что сам факт формирования нулей поля вне дальней зоны хорошо известен. Нули электромагнитного поля в окрестности фокуса оптических устройств изучались во многих работах, достаточно указать на монографию [1]. Из работ, посвященных анализу антенн, укажем на [2], в которой проведено теоретическое и экспериментальное исследование электрического поля в ближней зоне зеркальной антенны в облучателем в виде полуволнового вибратора и найдены глубокие минимумы, которые можно отождествить с нулями поля. Существование нулей в электромагнитных полях сложной структуры следует из асимптотических представлений полей специальными функциями Эйри, Пирси, и более общей теории спецфункций волновых катастроф [3,4].
Однако задача синтеза неподвижных нулей электрического (магнитного) поля в ближней зоне излучателя или системы излучателей возникла сравнительно недавно в связи с проблемой формирования области с минимальным значением поля вблизи антенн сотовых телефонов. Укажем на работу [5], в которой было показана возможность реализации нуля электрического поля на любом расстоянии от системы ортогональных электрического и магнитного диполей при определенном подборе амплитуд и фаз их дипольных моментов. Неподвижный нуль электрического поля в этом случае формируется на прямой, ортогональной плоскости расположения диполей и проходящей через центры диполей. В работах [6,7] был рассмотрен случай формирования одного неподвижного нуля электрического поля системой из двух параллельных вибраторов конечной длины. В цитированных работах результаты были получены на основе аналитических формул для полей указанных излучателей.
В работах [8,9] было показано, что системой ортогональных электрического и магнитного диполей может быть сформировано от одного до двух неподвижных нулей электрического поля. Также в [9] была рассмотрена возможность формирования М неподвижных нулей электрического поля системой N+M параллельных электрических диполей и конкретно изучен случай двух диполей. В данной статье рассматривается дальнейшее развитие результатов работы [9].
Ниже будем обсуждать только случай реализации неподвижных нулей электрического поля, так как условия реализации неподвижных нулей магнитного поля могут быть получены аналогичным образом. При этом ограничимся анализом гармонического режима возбуждения излучателей, хотя рассматриваемый нами подход может быть обобщен и на случай негармонического возбуждения. Так, возможность формирования неподвижного нуля электрического поля вблизи системы ортогональных электрического и магнитного диполей в импульсном режиме возбуждения была показана в [9].
Предположим, что задана система излучателей – электрических и магнитных диполей, взаимодействием между диполями пренебрегаем. В общем случае система N излучателей имеет 6N степеней свободы, половина которых определяется дипольными моментами (с учетом ориентации диполей в пространстве), половина – координатами точек расположения диполей. На эту систему следует наложить два вида требований: 1) требования к ДН системы и 2) задание координат точек пространства, в которых векторы электрического поля равны нулю. В такой постановке задача синтеза остается достаточно сложной, поэтому для выявления сути дела существенно упростим постановку задачи, отказавшись от требований к ДН и предполагая, что диполи параллельны друг другу. Дальнейшие упрощения постановки задачи будут обсуждаться по ходу дела. Используем метод комплексных амплитуд, временной множитель exp (iωt). Все линейные размеры нормированы умножением на волновое число свободного пространства.
Система параллельных электрических диполей
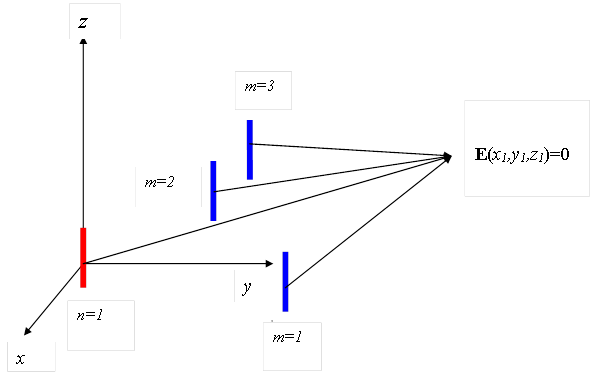
Пусть имеется N + M параллельных электрических диполей, расположенных в ограниченной области на различных расстояниях друг от друга. Первые N излучателей используются для формирования начальной ДН, остальные M излучателей - для формирования заданного числа нулей электрического поля в ближней и промежуточной зонах системы. Влияние полей М излучателей на результирующую ДН системы проверяется после определения дипольных моментов М излучателей, обеспечивающих формирование нулей электрического поля. Назовем N излучателей – базовыми, M излучателей – управляющими (рис.1).
Рис.1. Постановка задачи о формировании нуля электрического поля системой параллельных диполей. Показаны один базовый и три управляющих диполя
Далее положим, что центры всех диполей расположены в одной плоскости (х,у) и нули электрического поля формируются также в этой плоскости. Введем декартову и сферическую системы координат, привязанные к одному из базовых диполей. В любой точке плоскости, проходящей через центры диполей, базовые и управляющие диполи будут создавать только компоненты электрического поля Eθ. Для одного диполя в сферической системе координат, связанной с диполем, эта компонента электрического поля равна
где радиус R –расстояние от начала координат до точки наблюдения, параметр Р=Il - дипольный момент, константа А без ограничения общности полагается единице. Условия обращения в нуль электрического поля в М точках плоскости, с учетом того, что угол θ=90о, приводят к следующей системе линейных алгебраических уравнений относительно комплексных амплитуд дипольных моментов М диполей
В (2) дипольные моменты 
базовых диполей считаются
известными, дипольные моменты 
М управляющих
диполей неизвестны, заданы координаты точек расположения базовых и управляющих
диполей, а также координаты М нулей электрического поля. Таким образом,
все расстояния в (2) определены и (2) представляет собой систему линейных
алгебраических уравнений М-ого порядка относительно дипольных моментов
управляющих диполей.
Число неизвестных в (2) согласовано с порядком системы, поэтому система (2) имеет решение и притом единственное. На первый взгляд, из последнего утверждения следует, что число нулей электрического поля, определяемых решением системы (2) равно М - числу заданных при формулировке системы (2) положений нулей электрического поля. Однако это предположение ошибочно.
Рис.
2. Анализ вариантов формирования неподвижных нулей электрического поля
системой
из двух диполей при различных значениях амплитуд дипольных моментов:
а) Нули
отсутствуют, б) и в) реализуются два нуля поля, г), д) реализуется один нуль
поля, е) бесконечное число нулей.
Поясним ситуацию на примере двух диполей. На рис. 2 показаны положения двух диполей в плоскости (х,у) и линии уровня – окружности, на которых модули электрических полей двух диполей равны друг другу. Если окружности пересекаются, то подбором фаз дипольных моментов в этих точках можно скомпенсировать поля диполей и получить неподвижный нуль полного электрического поля. Из рис. 2 следует, что возможны 4 варианта формирования нулей, из которых два – являются общими, два – частными. Случай, когда нулей нет (окружности не пересекаются) показан на рис.2а, Общие случаи формирования нулей: окружности пересекаются в 2-х точках, причем эти точки либо находятся в полосе между диполями (рис.2б), либо вне этой полосы справа или слева от диполей (рис.2в). Частный случай: окружности касаются в одной точке, при этом точка касания находится либо между центрами диполей (рис.2г), либо на продолжении прямой, соединяющий центры диполей (рис.2д). Наконец, возможен исключительный случай, когда нули поля расположены точно на плоскости симметрии системы: на рис.2е - это прямая, проходящая перпендикулярно отрезку, соединяющему центры диполей, через его середину. Последний случай соответствует расположению диполя над идеально проводящей плоскостью, что эквивалентно ее замене зеркальным источником. Таким образом, с учетом симметрии системы и расположения точек нулевого поля число нулей электрического поля для данной системы диполей может принимать следующие значения: 0,1,2, ∞.
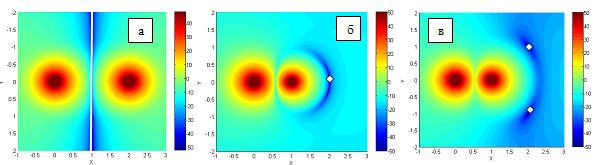
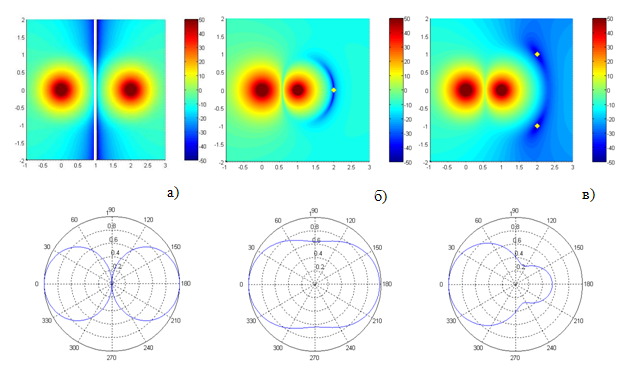
Рис. 3. Картины формирования нулей электрического
поля двумя диполями:
а) бесконечное число нулей (в плоскости), б) один нуль, в) два нуля
Нули показаны белой линией (а) и белыми ромбиками (б,в)
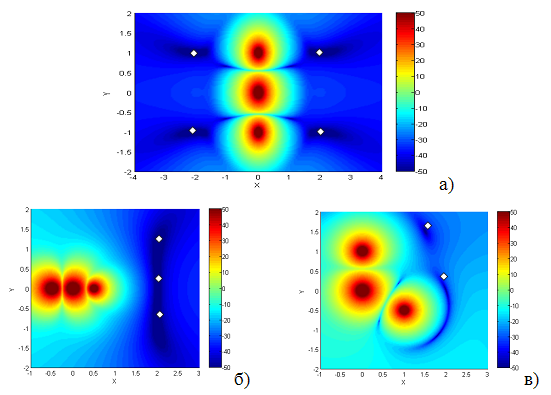
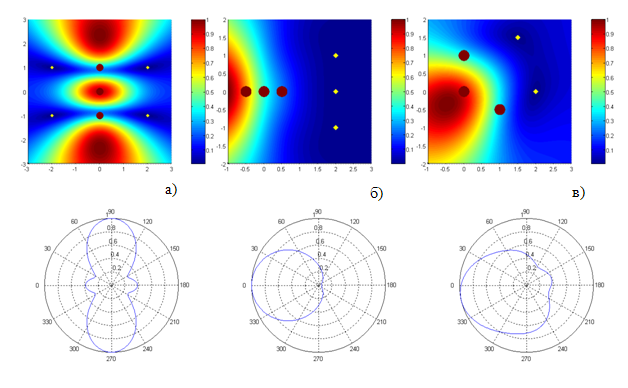
Рис. 4. Картины формирования нулей электрического поля тремя диполями:
а) 4 нуля, б) три нуля, в) два нуля.
Таблица 1. Координаты базового диполя (БД) ,
управляющих диполей (УД),
значения амплитуд и фаз их дипольных моментов и
координаты нулей электрического поля
|
рисунок |
базовый диполь |
управляющий диполь |
координаты нулей |
|||||||
|
координаты |
момент |
координаты |
момент |
|||||||
|
x |
y |
модуль |
фаза |
x |
y |
модуль |
фаза |
x |
y |
|
|
3а |
0 |
0 |
1 |
0 |
2 |
0 |
1 |
3.14 |
1 |
0 |
|
3б |
0 |
0 |
1 |
0 |
1 |
0 |
0.45 |
3.12 |
2 |
0 |
|
3в |
0 |
0 |
1 |
0 |
1 |
0 |
0.67 |
2.77 |
2 |
1 |
|
2 |
-1 |
|||||||||
|
4а |
0 |
0 |
1 |
0 |
0 |
1 |
0.55 |
-3.04 |
2 |
1 |
|
2 |
-1 |
|||||||||
|
0 |
-1 |
0.55 |
-3.04 |
-2 |
1 |
|||||
|
-2 |
-1 |
|||||||||
|
4б |
0 |
0 |
1 |
0 |
0.5 |
0 |
0.217 |
-2.78 |
2 |
0 |
|
-0.5 |
0 |
0.94 |
-2.98 |
2 |
1 |
|||||
|
2 |
-1 |
|||||||||
|
4в |
0 |
0 |
1 |
0 |
0 |
1 |
0.19 |
0.06 |
1.5 |
1.5 |
|
1 |
0.5 |
0.64 |
3.01 |
2 |
0 |
|||||
На рис. 3 в качестве примеров приведены распределения интенсивности электрического поля двух диполей в плоскости центров диполей (х.у), на рис. 4 – распределения интенсивности поля вблизи трех диполей. Координаты диполей и нулей поля, а также значения дипольных моментов приведены в табл. 1. Распределения интенсивности электрического поля на рисунках 3-5 даны в дБ. Показаны три случая, когда в системе двух диполей формируются нули электрического поля в плоскости (рис.3а), в одной (рис.3б) или двух (рис.3в) точках.
Обсудим теперь случай трех диполей, причем два диполя будем использовать, как управляющие для формирования нулей. В этом случае не удается реализовать наглядный графический анализ вариантов формирования нулей, аналогичный рассмотренному выше для двух диполей. Однако из соображений симметрии можно указать варианты расположения нулей поля, при которых число нулей вследствие симметрии больше числа управляющих диполей. Соответствующие примеры приведены на рис. 4, на котором показаны варианты реализации нулей электрического поля тремя диполями с числом нулей от 4-х до 2-х.
Были проведены также расчеты интенсивности поля в других сечениях пространства (x,z) и (y,z).
Аналогично были рассмотрены случаи реализации большего числа нулей электрического поля.
Таким образом, на основе разобранных примеров можно сделать вывод, что число S нулей поля, определяемых решением системы (2) с М управляющими диполями, подчиняется условию S≥M, причем число нулей, равное М, реализуется при несимметричном расположении излучателей. Случай двух диполей в этом отношении является исключительным, так как всегда имеет плоскость симметрии, проходящую через прямую, соединяющую центры диполей, параллельно осям диполей.
Из приведенных на рис. 3 расчетов следует, что изменением отношения амплитуд и разности фаз базового и управляющего диполей можно варьировать размеры области с минимальным значением поля, содержащей нули поля. При этом наибольший практический интерес представляет, по-видимому, формирование области с минимальным значением поля, содержащей два нуля, так как случай двух нулей – это случай общего положения, устойчивый относительно погрешности установки параметров и координат двух диполей. Случай формирования одного нуля также может быть интересен в практическом плане.
Показанные на рис. 4 варианты распределения интенсивности электрического поля для трех диполей также являются иллюстрацией приведенных выше утверждений.
Система параллельных электрических вибраторов
Проведенный выше наглядный анализ формирования нулей электрического поля системой из двух параллельных электрических диполей переносится на случай определения нулей электрического (магнитного) поля двух параллельных вибраторов конечной длины. Управляющими параметрами в случае вибраторов, помимо точек расположения вибраторов, являются амплитуды и фазы токов в точках питания вибраторов, а также длины вибраторов. Конкретные расчеты в случае системы вибраторов были проведены с использованием известных выражений для электрического поля тонких вибраторов конечной длины, приведенных в [10,11].
Результаты расчета интенсивности электрического поля в поперечной плоскости двух
параллельных вибраторов и диаграммы направленности приведены на рис. 5 для
вибраторов c длиной плеча 
, на рис. 6 для вибраторов с длиной плеча
/2.
Рис.5. Картины формирования нулей электрического поля двумя вибраторами с длинами плеч вибраторов L = 0,1. Положения базовых и управляющих вибраторов показаны темными кружками; нулей электрического поля – белыми ромбиками и линиями. Координаты вибраторов и нулей поля те же, что на рис. 3.
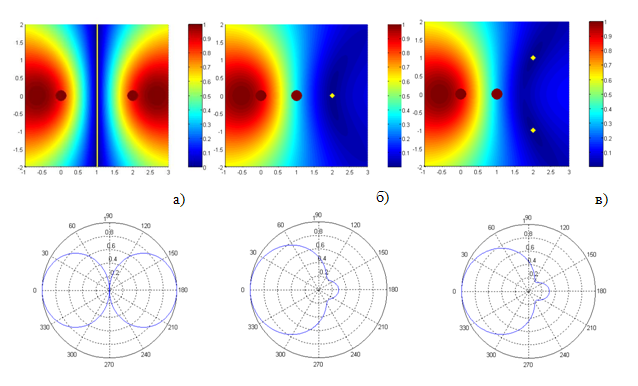
Рис.6. Картины формирования нулей электрического поля двумя вибраторами с длинами плеч вибраторов L = p/2. Координаты вибраторов и нулей поля те же, что на рис. 5.
Как следует из сравнения рис. 3 и 5, структура поля вблизи вибраторов конечной, но малой длины согласуется с расчетами поля вблизи диполей.
В случае полуволновых вибраторов модуль напряженности электрического поля спадает с увеличением расстояния заметно медленнее, чем для диполей. В связи с этим распределения интенсивности поля на рис. 6 и 7 приведены в линейной шкале в диапазоне значений от 1 до 0,1.
На рис. 7 приведены расчеты распределения интенсивности поля вблизи системы из трех полуволновых вибраторов и диаграммы направленности при тех же значениях положений нулей, что в случае трех диполей (сравните рис. 4 и 7).
Рис.7. Картины формирования нулей электрического поля тремя вибраторами с длинами плеч вибраторов L = p/2 и диаграммы направленности систем вибраторов. Координаты вибраторов и нулей поля те же, что на рис. 4.
Отметим, что увеличение длины вибраторов до половины длины волны (рис. 6,7) приводит к качественно новому эффекту по сравнению с элементарными вибраторами: появлению в ближней зоне максимумов напряженности электрического поля, смещенных относительно центров вибраторов.
Заключение
Проведенные расчеты иллюстрируют возможность создания областей с экстремальными значениями модуля электрического поля на конечном расстоянии от системы вибраторных антенн. Размеры области с минимальным значением поля, содержащей нули поля, варьируются при изменении управляющих параметров излучателей. Диаграммы направленности в поперечной плоскости системы близко расположенных вибраторов в зависимости от соотношений амплитуд и фаз токов в точках питания могут быть близки к изотропным, к однонаправленным или иметь несколько лепестков.
Предложенный подход обобщается на случаи формирования нулей электрического (магнитного) поля системой произвольно расположенных и произвольно ориентированных в пространстве элементарных излучателей или вибраторов конечной длины. При этом нули поля могут располагаться произвольным образом относительно излучателей.
В ближнем поле вибраторов конечной длины наряду с нулями электрического поля формируются области с максимальными значениями поля.
Методика формирования областей с малым значением электрического (магнитного) поля представляет интерес в различных приложениях: создание антенн сотовых телефонов и других средств мобильной связи, в минимальной степени влияющих на пользователя, решение вопросов электромагнитной совместимости антенн, использование принципов адаптации при отстройке от мешающих сигналов в системах ближней радиолокации.
1. Борн М., Вольф Э. Основы оптики. М.: Наука, 1979, 856 с.
2. Давыдов А.Г., Калошин В.А. Моделирование ближнего поля зеркальной антенны и его измерений датчиком в виде электрического вибратора./ Журнал радиоэлектроники, 2004, №3.
3. Кравцов Ю.А., Орлов Ю.И. Геометрическая оптика неоднородных сред. М.: Наука, 1980, 304 с.
4. Крюковский А.С., Лукин Д.С., Палкин Е.А. Специальные функции волновых катастроф. Препринт. /ИРЭ РАН СССР. –М.: 1984, №43 (415), 75 с.
5. Пермяков В.А., Голобородько А.С. Структура электромагнитного поля ортогональных электрического и магнитного диполей с произвольным соотношением токов. / Вестник МЭИ, 1999, № 5, с. 49-53
6. Каценеленбаум Б.З. , Левин Б.М. . Синтез антенн с областью малого поля в ближней зоне. /Антенны, №6(97), 2005, с. 38-46.
7. Левин Б.М. Поля линейных излучателей в ближней зоне. /Радиотехника и электроника, 2011, т.56 № 1, с. 34-42.
8. Пермяков В.А., Корюкин А.Н. Качественный анализ электромагнитных полей обобщенного элемента Гюйгенса. /Нелинейный мир, 2008, т.6, № 4, с.296-299.
9. Корюкин А.Н. Качественный анализ электромагнитных полей простых антенн. /Дисс. на соискание ученой степени к.т.н. -М.: МЭИ(ТУ), 2008.
10. Марков Г.Т. Антенны. -М.: ГЭИ, 1960, 535 с.
11. Стреттон Дж.А. Теория электромагнетизма. -М-Л.: Огиз-Гостехиздат, 1948, 540 с.