УДК 621.396.67

СОБСТВЕННЫЕ КОЛЕБАНИЯ РЕЗОНАТОРА НА ОСНОВЕ ЭЛЕКТРОМАГНИТНОГО КРИСТАЛЛА

 

С. Е. Банков, М. Д. Дупленкова, Е. В. Фролова

ИРЭ им. В.А. Котельникова РАН

Получена 16 июля 2013 г.

 

Аннотация. Рассматривается задача о собственных колебаниях резонатора на основе электромагнитного кристалла в виде решетки металлических цилиндров с сосредоточенными управляемыми емкостными элементами, расположенной внутри плоского волновода. Исследуется резонатор, образованный путем формирования дефектов в решетке электромагнитного кристалла. В качестве дефектов используются один или несколько рядов решетки с емкостями отличными от емкостей регулярного кристалла. Анализируется спектр собственных частот и свойства собственных колебаний. Проводится оптимизация параметров резонатора, обеспечивающая существование кратных резонансных частот, необходимых для эффективной реализации нелинейных эффектов в резонаторе.

Ключевые слова: электромагнитный кристалл, нелинейный электромагнитный кристалл, генерация второй гармоники, собственные колебания, резонансные частоты.

Abstract. An eigen value problem for resonator on the base of electromagnetic crystal is considered. The electromagnetic crystal is formed by an array of metal cylinders with lumped capacitive elements placed inside parallel plate waveguide. The resonator is formed by defects of array of electromagnetic crystal. One or several infinite rows of the array with capacitors differ from capacitors of regular crystal are used to form defects. Spectrum of resonance frequencies and properties of eigen modes are analyzed. Parameters of the resonator are optimized to obtain conditions for effective non-linear interactions in the resonator.

Keywords: electromagnetic crystal, non-linear electromagnetic crystal, second harmonic generation, eigen modes, resonance frequencies.

 

1.     Постановка задачи

Данная работа посвящена исследованию взаимодействия электромагнитных волн в нелинейных периодических структурах СВЧ диапазона, получивших название электромагнитных кристаллов (ЭМК). Она является развитием работ [1 – 5], в которых исследовались ЭМК, образованные решеткой металлических цилиндров, расположенных внутри плоского волновода (ПВ), под которым понимаются два идеально проводящих параллельных друг другу экрана. Цилиндры имеют зазоры, в которые включены нелинейные емкостные элементы.

В работе [1] построена модель нелинейного ЭМК конечной длины по одной координате в виде системы нелинейных уравнений, а в работе [2] получено приближенное решение системы для полубесконечного ЭМК. В работе [3] представлены результаты численного и аналитического исследования нелинейного ЭМК в режиме пространственного синхронизма двух прямых волн, распространяющихся внутри структуры на основной и удвоенной частотах. В работах [4]  и [5] исследуется режим пространственного синхронизма прямой и обратной волн, которые распространяются соответственно на основной и удвоенной частотах. Пространственный синхронизм прямой и обратной волн представляет особый интерес, так как он реализуется в ЭМК данного типа значительно проще, чем пространственный синхронизм двух прямых волн. Численное исследование этого режима представлено в [4], а аналитическое в [5].

В работах [6,7] рассматриваются нелинейные взаимодействия волн свободного пространства с волнами ЭМК, которые реализуются в, так называемых, излучающих ЭМК. Для этого элементы кристалла соединяются с излучателями, способными принимать волны из окружающей среды. В указанных работах показано, что для достижения сильных нелинейных эффектов, таких как генерация кратных гармоник, параметрическое усиление и преобразование частоты необходимо выполнить условия пространственного синхронизма волн свободного пространства и волн ЭМК.

Следует отметить, что режим пространственного синхронизма относится к числу режимов накопления, в которых малые нелинейные эффекты на отдельных элементах кристалла усиливаются за счет их когерентного сложения. Наряду с ним известен другой режим накопления – резонансный. Он возникает в высокодобротных объемных резонаторах, которые имеют собственные частоты, совпадающие с комбинационными частотами, сигналы на которых возникают благодаря нелинейным взаимодействиям. В простейшем случае эффекта генерации кратных гармоник комбинационные частоты кратны основной частоте, на которой возбуждается нелинейная система.

Следующим этапом исследования нелинейных ЭМК является изучение их поведения в резонансном режиме. Для этого внутри ЭМК должен быть сформирован достаточно высокодобротный резонатор, обладающий требуемым спектром частот. Наиболее естественным средством формирования высокодобротного резонатора в ЭМК является внесение в его структуру дефектов [8], то есть элементов, имеющих свойства отличные от свойств элементов регулярного кристалла. В структуре, которая изучалась в отмеченных выше работах, формирование дефектов проще всего достигается изменением значений емкостей, включенных в металлические цилиндры. Оно может быть получено вариацией постоянных управляющих напряжений на элементах ЭМК без изменения его структуры.

Для создания резонатора важна также форма дефекта. Мы будем рассматривать одну из простейших форм: плоско – слоистую. Для ее выполнения емкости меняются в бесконечном ряде элементов ЭМК. Резонатор может быть образован одним или несколькими такими рядами.

Целью данной работы является изучение свойств линейных резонаторов внутри ЭМК и поиск его параметров, обеспечивающих условия для реализации интенсивного эффекта генерации кратных гармоник.

 

2.     Модель резонатора в ЭМК

       Исследуемая структура показана на рис. 1. Она бесконечна вдоль оси 0у и может иметь конечные размеры по оси 0х. Металлические цилиндры расположены в узлах прямоугольной сетки с периодами . Всего в структуре имеется  бесконечных рядов цилиндров. Из них только  рядов образуют резонансную область, в которой накапливается электромагнитная энергия. Они расположены внутри структуры и отделены от ее границ несколькими слоями, которые обеспечивают связью резонатора с внешним пространством при  и . В общем случае число слоев связи слева и справа  и  может быть разным.

       Слои в центральной части резонатора отличаются от слоев связи значением емкостей. Конденсаторы в них могут иметь разные номиналы , . Номиналы конденсаторов в слоях связи  имеют одинаковые значения.

       Математическую модель резонатора на основе ЭМК описанного выше вида удобно построить, используя модель, описанную в работах [1 – 5]. Поскольку мы исследуем линейный резонатор, то нас интересуют уравнения, описывающие линейную задачу. Они имеют следующий вид:

       ,                                                                                (1)

где  - вектор, описывающий возбуждение структуры,  - вектор размерностью , включающий напряжения на емкостях, включенных в цилиндры,  - диагональная матрица, включающая проводимости емкостей,  - матрица, описывающая взаимодействие цилиндров в решетке.

 

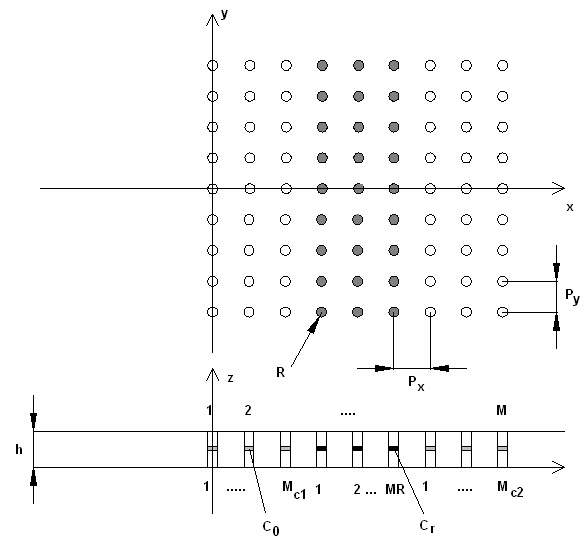
Рис. 1. Исследуемая структура

 

       Элементы матрицы  определяются через параметры структуры следующим образом:

       ,                                                                                           (2)

         ,

,

, ,

,

,

            ,

 

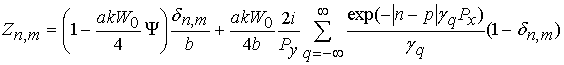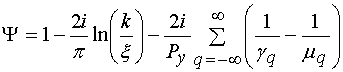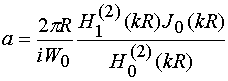где  - символ Кронекера,  - функции Ганкеля второго рода,  - функция Бесселя,  - волновое число среды внутри ПВ,  - радиус цилиндров,  - высота ПВ. Параметр  выбирается произвольно таким образом, чтобы выполнялось неравенство:

         .

         Модель (1),(2) построена для описания квазипериодического режима в структуре, в котором поля подчиняются следующим условиям:

         ,                                                      (3)

где  - параметр квазипериодического режима, задающий сдвиг фаз между полями в соседних по оси 0у периодах. Отметим, что квазипериодический режим соответствует возбуждению структуры плоской волной, падающей на нее под углом падения  относительно оси 0х:

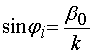         .                                                                                    (4)

         При исследовании собственных колебаний резонатора вектор  следует положить равным нулю. Тогда мы приходим к однородной системе линейных алгебраических уравнений (СЛАУ):

         .                                                                               (5)

         Собственные частоты находим из условия существования нетривиальных решений СЛАУ (5):

         .                                                                             (6)

         Уравнение (6) назовем характеристическим уравнением резонатора. Решение однородной СЛАУ (5) кроме собственных частот, позволяет также найти собственные вектора , элементы которых – это значения напряжений на емкостях.

         Собственные или резонансные частоты , полученные как корни уравнения (6), являются комплексными числами даже в отсутствие потерь в резонаторе, так как имеются потери на излучение в окружающее резонатор пространство. Эти потери говорят о том, что резонатор имеет конечную добротность, которая является добротностью связи :

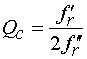         ,                                                                                     (7)

         .

 

3.     Однослойный резонатор

В этом разделе мы рассмотрим свойства однослойного резонатора с . Будем исследовать структуры, у которых слои связи образуются цилиндрами без конденсаторов, что соответствует  . На рис. 2 показана зависимость резонансной частоты  от емкости . Кривые 1 – 3 соответствуют . Они получены для , , , , , . Здесь и далее все размеры приводятся в миллиметрах, а емкости в пикофарадах.

 

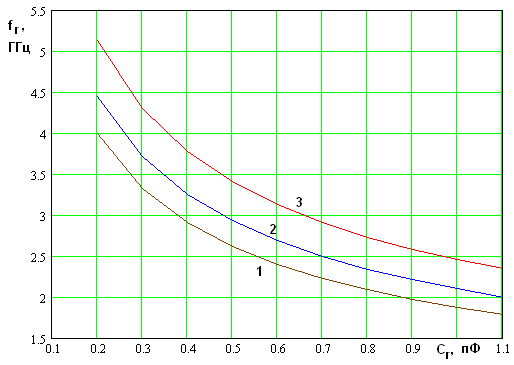
Рис. 2. Зависимость резонансной частоты от емкости при разных радиусах цилиндров

 

       Из рис. 2 видно, что с увеличением емкости конденсаторов, включенных в элементы слоя, образующего резонансную область частота  существенно уменьшается. При этом уменьшение радиуса цилиндров также приводит к уменьшению резонансной частоты.

       Отметим, что характерный размер резонансной области совпадает с периодом структуры . В рассматриваемом примере он равен 6 мм.  Таким образом, видно, что резонанс в структуре наблюдается на длинах волн, которые существенно больше размера резонансной области. Мы можем сделать вывод, что наблюдаемый резонанс имеет природу близкую к квазистатической. Резонатор можно рассматривать как некоторый контур. Роль емкости в нем играет емкость в цилиндре, а роль индуктивности собственная индуктивность цилиндра и вносимые индуктивности от соседних цилиндров.

       С этой точки зрения уменьшение резонансной частоты (см. рис. 2) аналогично уменьшению резонансной частоты контура, которое происходит при увеличении его емкости.

       Квазистатическую природу резонанса в ЭМК подтверждает также исследование частот высших типов колебаний, которые отсутствуют в полосе частот до 16 – 18 ГГц. Таким образом, отношение резонансных частот высшего и основного типов колебаний в рассматриваемом примере достигает восьми, что характерно для квазистатических резонаторов.

       Дополнительным фактором, который способствует разрежению спектра колебаний анализируемой структуры, является отражающая способность ЭМК. Колебания в резонаторе возникают благодаря тому, что ЭМК, составленный из металлических цилиндров находится в полосе запирания. Введение в него слоя цилиндров с конденсаторами с конечной емкостью создает условия для накопления энергии в окрестности этого слоя. Однако, за пределами указанной полосы запирания условия для возникновения резонанса отсутствуют. Поэтому появление высокодобротных колебаний на частотах выше верхней границы полосы запирания маловероятно. Возможно, что отсутствие высших типов колебаний обусловлено также и этим фактором.

       Модель квазистатического резонатора также позволяет качественно объяснить уменьшение частоты при уменьшении радиуса металлических цилиндров, которое приводит к росту их индуктивности. В свою очередь, увеличение индуктивности контура уменьшает его резонансную частоту.

       На рис. 3 показана зависимость добротности  от емкости . Кривые 1 – 3 соответствуют . Они получены для параметров, указанных выше. Видно, что с ростом емкости, а, следовательно, с уменьшением резонансной частоты  добротность растет. Увеличение добротности при уменьшении частоты  связано с изменением отражающих свойств слоев связи. Выше было отмечено, что они образуют периодическую структуру, функционирующую в полосе запирания [8]. При этом в ней отсутствуют распространяющиеся волны. Есть только волны с экспоненциальным затуханием. В работе [8] показано, что постоянная затухания такой волны растет при уменьшении частоты. Благодаря этому энергия на низких частотах проникает через слой связи в окружающее пространство слабее, чем на высоких частотах, что объясняет обсуждаемое поведение добротности резонатора.

 

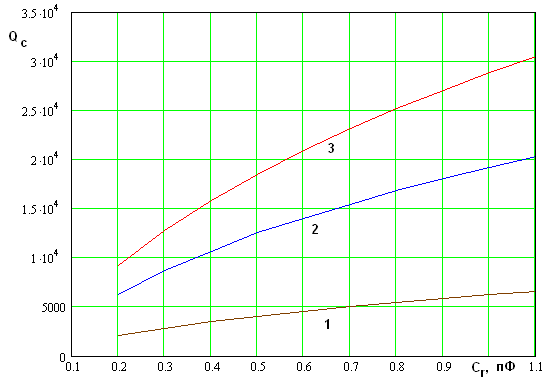
Рис. 3. Зависимость добротности связи от емкости при разных радиусах цилиндров

 

         На рис. 4 и 5 показаны зависимости резонансной частоты и добротности от емкости , полученные для разного числа слоев связи: . Им соответствуют кривые 1 – 3. Радиусы цилиндров . Остальные параметры приведены выше. Из рис. 4 видно, что резонансная частота слабо зависит от размеров области связи. На рис. 5 кривая 1  соответствует добротности , кривая 2 добротности  умноженной на параметр , а кривая 3 добротности умноженной на . Видно, что кривые 1 – 3 незначительно отличаются друг от друга. Из этого можно сделать вывод о том, что зависимость добротности от параметра  имеет экспоненциальный характер. Такое ее поведение легко объясняется зависимостью поля от координаты x в области связи. Поле в этой области имеет характер экспоненциально затухающей волны. Поэтому при увеличении числа слоев связи энергия, излучаемая из резонатора во внешнее пространство уменьшается экспоненциально, а добротность, соответственно, экспоненциально возрастает.

 

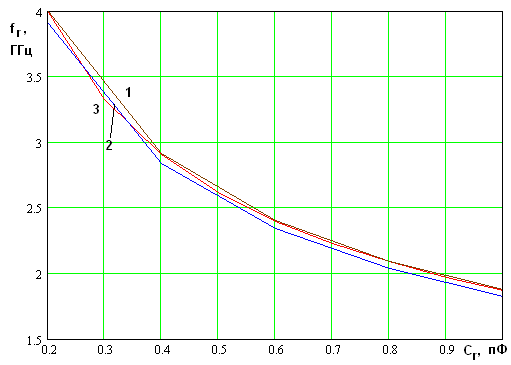
Рис. 4. Зависимость резонансной частоты от емкости при разном числе элементов связи   

 

  

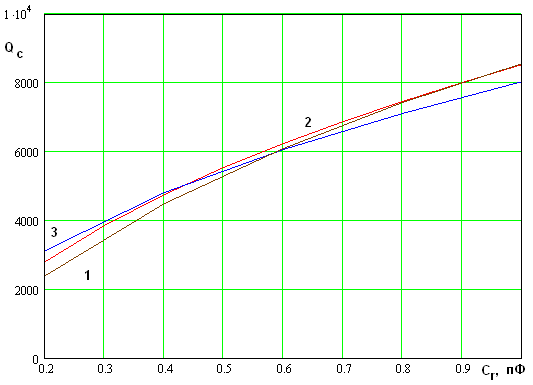
Рис. 5. Зависимость добротности связи от емкости при разном числе элементов связи

 

       Следующие два рисунка 6 и 7 показывают влияние на резонансную частоту периодов ЭМК. На рис. 6 представлена ее зависимость от периода , полученная при , , , . Можно отметить весьма слабое влияние данного параметра на резонансную частоту, которая меняется не более чем на 10% при увеличении периода в шесть раз.

       На рис. 7 показана зависимость резонансной частоты от периода , которая получена при . Резонансная частота уменьшается при увеличении периода ЭМК. Существенная зависимость параметра  от  и ее характер объясняются тем, что в отличие от периода  период  непосредственно определяет размер резонансной области, увеличение которой уменьшает резонансную частоту.

 

Рис. 6. Зависимость резонансной частоты от периода

 

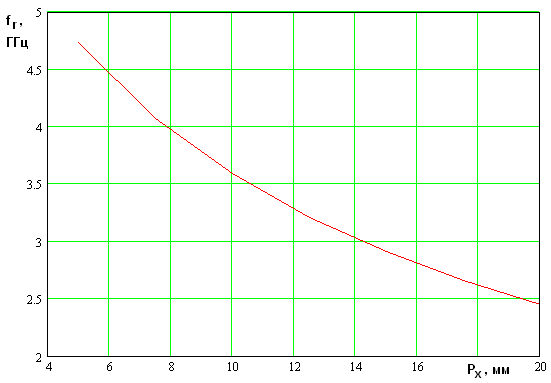
Рис. 7. Зависимость резонансной частоты от периода

 

      

Рис. 8. Зависимость резонансной частоты от угла падения

 

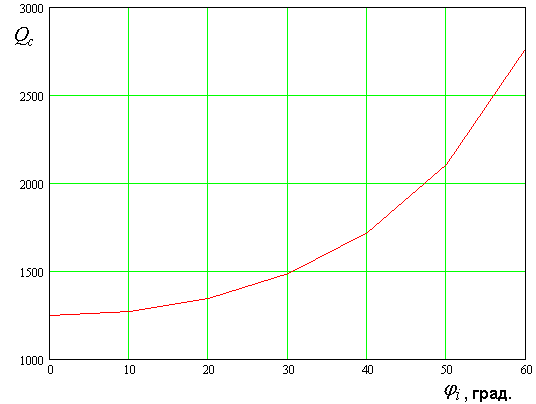
Рис. 9. Зависимость добротности от угла падения

 

       На рис. 8,9 показаны зависимости резонансной частоты и добротности от угла падения . Отметим, что в задаче на собственные частоты возбуждающая плоская волна, которая характеризуется углом падения, отсутствует. Поэтому возникает вопрос о смысле данного параметра. Особенностью бесконечной периодической по оси 0у структуры является то, что ее поле удовлетворяет условию периодичности (3), в которое входит параметр . Этот параметр задает сдвиг фаз между полями в соседних периодах. В общем случае  меняется в пределах, определяемых неравенством:

       .                                                                                              (8)

       Таким образом, уравнение (6) и его корни  непрерывно зависят от параметра . Отсюда следует, что спектр собственных частот резонатора не дискретный, а непрерывный. При возбуждении резонатора плоской волной параметр  фиксируется, так как он определяется ее углом падения. Таким образом, источник возбуждения выделяет из непрерывных спектров частот и собственных колебаний одно выделенное колебание со своей частотой.

       Таким образом, исследование зависимостей параметров  и  от угла падения , по – существу, является исследованием их зависимостей от параметра , поскольку они связаны соотношением (4). При этом предпочтение углу  отдано по причине большего удобства его применения.

       Кривые на рис. 8,9 получены при , , , , , , . Видно, что резонансная частота почти не меняется при изменении угла падения . При этом добротность существенно увеличивается при его росте от 0 до . В многих случаях независимость резонансной частоты от угла падения можно рассматривать как положительный фактор.

       На практике резонатор имеет конечные размеры и возбуждается не плоскими волнами, а широкими волновыми пучками. Такие пучки можно рассматривать как набор плоских волн со спектром, сосредоточенным в узкой области пространственных частот . Если парциальные плоские волны резонируют на сильно отличающихся частотах, то пучок после прохождения резонатора будет сильно отличаться от возбуждающего пучка. Наоборот, постоянство резонансной частоты позволяет ожидать незначительных искажений прошедшего через резонатор пучка.

       Важным фактором для резонансной системы являются тепловые потери. Их учет связан с расчетом электрических токов, текущих по поверхностям металлических цилиндров и экранам ПВ. Полное решение этой задачи связано с весьма трудоемкими расчетами. Однако, в рассматриваемой структуре имеется другой источник тепловых потерь, которые, как правило, превышают потери в металлических элементах конструкции. В тоже время, учет их осуществить значительно проще. Этот источник сосредоточен в емкостных элементах. Обычно такие элементы выполняются в виде полупроводниковых диодов. Их эквивалентная схема содержит последовательно соединенное с емкостью сопротивление базы .

       При наличии внутренних потерь в резонаторе его добротность  уже не является добротностью связи . Собственная добротность резонатора  имеет конечное значение. Она связана с параметрами  и  известным образом:

       .

       Рассмотрим как меняется собственная добротность однослойного резонатора от сопротивления базы . На рис. 10 показана зависимость параметра  от .

 

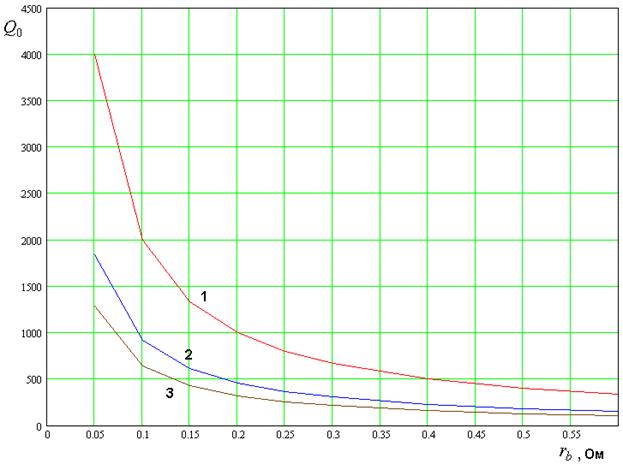
Рис. 10. Зависимость собственной добротности от сопротивления базы

 

       Кривые 1 – 3 на рис. 10 соответствуют . Они получены для , , , , . Видно, что большая добротность достигается при меньших значениях емкости. Такая зависимость объясняется тем, что меньшая емкость имеет большее реактивное сопротивление. Благодаря этому вклад активного сопротивления базы в общую проводимость емкости уменьшается, а добротность растет.

       Типичные для управляемых емкостей значения параметра  лежат в диапазоне 0.05 – 0.4 Ом. Отсюда следует, что достаточно высокие значения собственной добротности в несколько сотен и даже тысяч могут быть реализованы в СВЧ диапазоне.

 

4.     Двухслойный резонатор

       Однослойный резонатор очевидно бесполезен с точки зрения достижения основной цели нашей работы – создания резонатора с кратными частотами, так как в широком диапазоне он имеет единственное колебание. Увеличивая размер резонансной области путем увеличения параметра  мы сгущаем спектр собственных частот и создаем более благоприятные условия для решения поставленной задачи.

       Численные расчеты показали, что создание двухслойных резонаторов с кратными резонансными частотами возможно. Для описания их свойств введем параметр :

       ,                                                                                         (9)

где  - частоты первого и второго колебаний. Также полезно ввести параметр :

       ,                                                                                         (10)

который равен отношению емкостей конденсаторов.

 

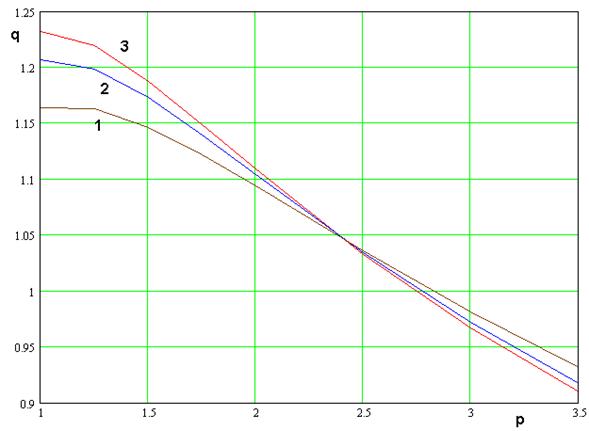
Рис. 11. Зависимость отношения резонансных частот  от параметра

 

Рис. 12. Зависимость резонансных частот от параметра

 

       Расчеты показали, что для достижения равенства параметра  единицы принципиально важно иметь разные значения емкостей. Об этом говорят кривые 1 – 3 на рис. 10. На рис. 11 показана зависимость параметра  от параметра . Кривые 1 – 3 соответствуют . Они получены при , , , , , .

       На рис. 12 показана зависимость резонансных частот от параметра . Кривые 1 и 2 соответствуют . Из рис. 10 видно, что равенство  достигается при . Это значение слабо зависит от абсолютной величины емкости.

       Интересно проследить зависимость параметров резонатора от угла падения .

 

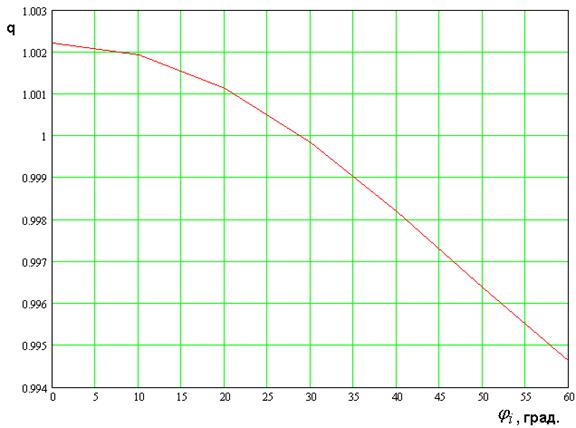
Рис. 13. Зависимость параметра  от угла падения

 

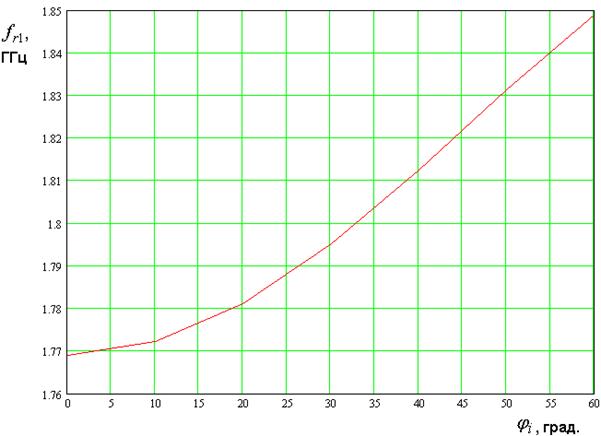
Рис. 14. Зависимость резонансных частот от угла падения

 

       На рис. 13 показана зависимость отношения резонансных частот  от угла падения. Она получена при тех же параметрах, что и раньше, а также  и . Видно, что угол падения практически не меняет величину . На рис. 14 показана зависимость резонансной частоты  от . Видно, что сама резонансная частота меняется сильнее отношения частот. Это означает, что при изменении угла падения частоты  двигаются синхронно, сохраняя их отношение практически неизменным.

 

5.     Трехслойный резонатор

 

       Рассмотрим далее свойства трехслойного резонатора с . Поскольку зависимости резонансных частот и добротностей от таких параметров как периоды решетки, число элементов связи и т.д. мало зависят от числа слоев, формирующих резонатор, то наибольший интерес представляют их зависимости от емкостей .

       Изучим поведение резонансных частот при изменении величины емкости, расположенной на краю резонатора . В силу симметрии структуры зависимости резонансных частот от емкости , находящейся на другом краю структуры будут иметь такой же вид.

       На рис. 15 показана зависимость резонансной частоты от величины емкости . Кривые 1 – 3 соответствуют . Они получены для , , , , , .

 

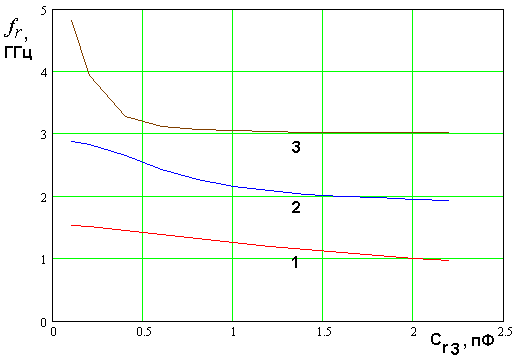
Рис. 15. Зависимость резонансной частоты от емкости

 

       Отметим, что изменении емкости  влияет на частоты всех трех колебаний резонатора. Такое их поведение обусловлено структурой собственных колебаний. Качественно она показана на рис. 15. Вертикальные линии отображают амплитуду напряжения на конденсаторе, а три разные их комбинации соответствуют разным колебаниям.

       Распределения, изображенные на рис. 16 получены для симметричного резонатора, у которого =.

Рис. 16. Распределение напряжений на конденсаторах в собственных колебаниях трехслойного резонатора

 

       Приведенные на рис. 16 распределения лишь качественно отображают картину поля в исследуемой структуре. Конкретное соотношение амплитуд напряжений зависит от значений емкостей. Из рис. 16 видно, что в спектре собственных колебаний имеются два симметричных колебания и одно антисимметричное (третье). При этом напряжение  у антисимметричного колебания равно нулю.

       Поскольку напряжение  у всех колебаний имеет ненулевую амплитуду, то все частоты  зависят от емкости .

 

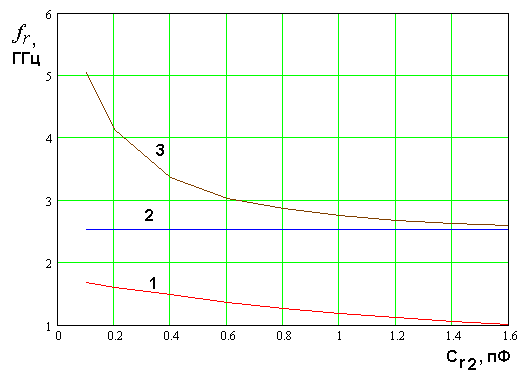
Рис. 17. Зависимость резонансной частоты от емкости

 

       Иная ситуация наблюдается в симметричном резонаторе при изменении емкости . Зависимость резонансных частот для этого случая показана на рис. 17. Кривые 1 – 3 как и на рис. 14 соответствуют . Они получены при тех же параметрах, что и раньше, но емкость  теперь постоянна и равна 0.5.

       Видно, что частота  не зависит от емкости . При увеличении емкости резонансные частоты уменьшаются. Крутизна их зависимости также уменьшается при больших емкостях. Это связано с тем, что сопротивление конденсатора при этом стремится к нулю и резонансная частота приближается к своему предельному значению, соответствующему короткозамкнутому цилиндру.

       Трехслойный резонатор также как и двухслойный может быть использован как колебательная система с кратными частотами. Введем следующие параметры:

       ,

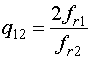       ,                                                                                       (11)

       .

 

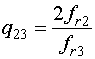       С их помощью можно количественно оценить достижение требуемого результата. Чем ближе каждый из введенных параметров к единице, тем ближе отношение резонансных частот к отношению натуральных чисел.

 

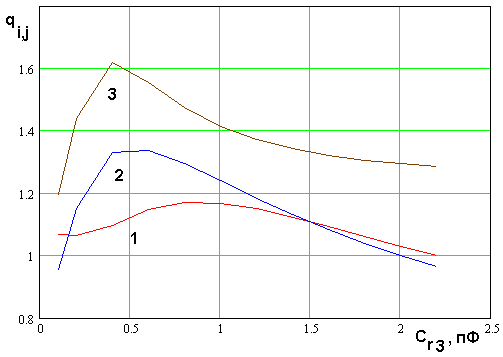
Рис. 18. Зависимость отношения резонансных частот от емкости

 

       На рис. 18 показаны зависимости параметров (11) от емкости . Кривые 1 – 3 соответствуют . Они получены для тех же параметров, что и кривые на рис. 14. Видно, что в трехслойном резонаторе при относительно малой емкости  можно получить резонансные частоты первого и третьего колебаний, находящиеся в отношении 1:3. Этот же результат достигается при больших емкостях. Интересно, что в том же диапазоне значений  можно получить отношение второй и первой резонансных частот равное двум. Параметр  обратить в единицу путем вариации емкости  не удается.

 

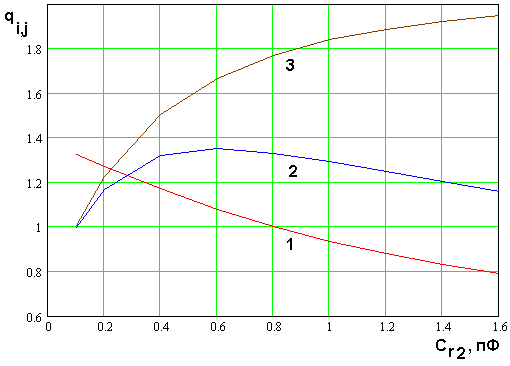
Рис. 19. Зависимость отношения резонансных частот от емкости

 

       На рис. 19 показана зависимость параметров  от емкости , которым соответствуют кривые 1 – 3. Они получены для тех же параметров, что и кривые на рис. 17. Интересно, что варьируя только емкость , можно получить два резонатора, у которых резонансные частоты  находятся в отношении 1:2. У одного резонатора с =0.8 такое отношение достигается для резонансных частот  и , а у другого для частот  и , но уже при =0.11. При этом частота  одинакова в первом и втором резонаторах.

       Отношение резонансных частот трехслойного резонатора весьма слабо зависит от угла падения  аналогично двухслойному резонатору (см. рис. 14). Этот вывод следует из рис. 20, на котором показана зависимость параметра  от угла . Она получена при  и =0.8.

 

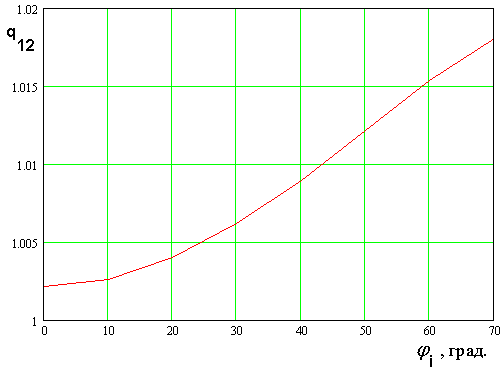
Рис. 20. Зависимость отношения резонансных частот от угла падения

 

Заключение

       Таким образом, проведенное исследование позволяет сделать два вывода. Первый из них состоит в том, что в ЭМК из металлических цилиндров с емкостными элементами можно создавать достаточно высокодобротные резонаторы. Второй вывод заключается в возможности создания резонаторов на основе ЭМК с кратными резонансными частотами, которые могут использоваться для реализации нелинейных эффектов умножения частоты.

 

        Работа выполнена при поддержке Российского фонда фундаментальных исследований. Проект № 11-08-00215-а.

 

Литература 

1. Банков С.Е. Модель нелинейного электромагнитного кристалла // РЭ. 2011. Т.56. №3. С. 261.

2. Банков С.Е. Полубесконечный нелинейный электромагнитный кристалл // РЭ. 2011. Т.56. №5. С. 1-11.

3. Банков С.Е. Взаимодействие прямых волн в нелинейном электромагнитном кристалле // Журнал радиоэлектроники. 2011. №3. http://jre.cplire.ru/jre/mar11/1/text.html.

4. Банков С.Е. Численное исследование взаимодействия прямой и обратной волн в нелинейном электромагнитном кристалле // Успехи современной радиоэлектроники. 2011. №5. С. 31-43.

5. Банков С.Е. Аналитическое исследование двухчастотного взаимодействия прямой и обратной волн в нелинейном электромагнитном кристалле // РЭ. 2011. Т.56. №8. С. 909-919.

6. Банков С.Е. Численное исследование взаимодействия волн в нелинейном излучающем электромагнитном кристалле // РЭ. 2011. Т.56. №9. С. 1044-1056.

7. Банков С.Е. Аналитическое исследование двухчастотного взаимодействия волн в нелинейном излучающем электромагнитном кристалле // РЭ. 2012. Т.57. № 5. С. 578-589.

8. Банков С.Е. Повороты волноводов на разреженных двумерных PBG кристаллах. // Радиотехника и электроника. 2005, Т. 50, №1. С. 41-47.