УДК 621.391, 621.396

СИСТЕМА ОРТОГОНАЛЬНЫХ СИГНАЛОВ ДЛЯ НЕКОГЕРЕНТНОГО ПРИЕМА СВЕРХШИРОКОПОЛОСНЫХ ХАОТИЧЕСКИХ РАДИОИМПУЛЬСОВ В МНОГОЛУЧЕВОМ КАНАЛЕ

 

Л. В. Кузьмин, Р. Ю. Емельянов

Институт радиотехники и электроники им. В.А. Котельникова РАН

Статья получена 26 июня 2014 г.

 

Аннотация.  Предложен и проанализирован новый метод приема сверхширокополосных хаотических радиоимпульсов в канале с многолучевым распространением. Метод основан на синтезе ортогонального базиса, на который проецируется принимаемый хаотический сигнал. Показано, что осуществление такого приема связано со свойствами хаотических колебаний, генерируемых детерминированной динамической системой. Установлено, что данный подход по вероятности ошибки на бит в канале с белым шумом и многолучевым распространением идентичен энергетическому приему.

Ключевые слова: хаотические радиоимпульсы, многолучевое распространение, метод приёма, сверхширокополосные системы связи.

Abstract: The new type of receiver of chaotic radiopulses is proposed and analyzed in multipath channel. It is based on projection of the received signal on specially synthesized orthogonal basis. The existence of this receiving method is related to chaotic oscillations properties, generated by deterministic dynamic system. Also, the identity of bit error rate in proposed and energetic receiving methods is established.

Key words: chaotic radiopulses, multipathing, ultrawideband communication systems.

 

Введение

Сверхширокополосные (СШП) хаотические радиоимпульсы сверхвысокочастотного (СВЧ) диапазона применяются для передачи информации в беспроводных системах связи [1] малого радиуса действия. Такой сигнал имеет малое время когерентности, что приводит к практически полному отсутствию замираний, вызываемых многолучевым распространением сигнала в беспроводных каналах связи, а это, в свою очередь увеличивает отношение сигнал/шум в точке приема в таких каналах по отношению к каналу с одним (прямым) лучом [2]. Применяемый на сегодняшний день энергетический прием СШП хаотических радиоимпульсов реализует это свойство, но он не обладает фильтрующими свойствами по отношению к посторонним сигналам, которые могут попасть в сверхширокую полосу частот хаотического сигнала. В связи с этим, интерес представляет разработка методов приема хаотического сигнала, которые бы позволили избирательно его принимать в условиях многолучевого распространения. С теоретической точки зрения для решения этой задачи наиболее привлекательными являются когерентные методы, однако их реализация связана с практической сложностью повторения формы хаотического сигнала в приемнике и в передатчике из-за экспоненциального разбегания хаотических траекторий, стартующих с незначительно различающихся начальных условий.

2. Метод приема

В рассматриваемой здесь схеме передачи информационные символы кодируются хаотическими радиоимпульсами – фрагментами хаотического сигнала длительности T_P, занимающими определенную временную позицию. Как было показано [3], хаотический радиоимпульс длительности T_P может быть представлен в виде взвешенной суммы взаимно ортогональных на длительности импульса сигналов, вид которых не зависит от реализации конкретного радиоимпульса, а зависит лишь от режима колебаний (периодического или хаотического), в котором находится источник (генератор) хаоса. Этот факт может быть использован для организации некогерентной схемы приема хаотических радиоимпульсов. А именно, принимаемый хаотический радиоимпульс, прошедший канал, проецируется на базис из системы ортогональных сигналов, который сформирован из хаотических колебаний. Такой способ позволяет осуществлять прием в канале с одним лучом, на фоне действия белого шума в приемнике [3].

Предпосылкой для успешного применения данного метода в многолучевом канале является некогерентное суммирование хаотических сигналов в точке приема, линейность рассматриваемого метода и вытекающая из этого возможность независимой обработки каждого пришедшего в приемник луча без знания точной формы хаотических колебаний, попадающих в приемник.

Способ создания такой системы сигналов основан на методе Карунена-Лоэва (методе главных компонент), который позволяет для аттракторов динамических систем синтезировать базис, хорошо отражающий структуру аттрактора [4]. В данном случае речь идет о представлении фрагмента хаотического сигнала x(t), 0 < t < T_P, через набор взаимно ортогональных на длительности импульса сигналов: , 0 < t < T_P, где каждая функция b_p может быть аппроксимирована собственным вектором ковариационной матрицы B'B

B'Bb_j = λ_jb_j,                                                (1)

где j = 1...M. Ковариационная матрица определяется как B'B = (X₁, X₂, …, X_N)×(X₁, X₂, …, X_N)'/N, где X_i – векторы пространства вложения, полученные путем взятия отсчетов хаотической траектории x(t) через временные интервалы Δt: X_i = (x(t_i), x(t_i + Δt), x(t_i + 2Δt),..., x(t_i + (M–1)Δt)). Первый вектор X₁ в M –мерном пространстве образован из M подряд идущих элементов хаотической последовательности (с 1 по M), второй образован элементами со 2 по M+1 и т.д. Длительность каждого вектора X_i, представляющего дискретизированный с шагом Δt участок хаотического сигнала, равна длительности хаотического радиоимпульса: T_P = MΔt. Ранг матрицы B'B равен размерности пространства вложения (M), она симметрична и обладает ортогональным базисом из собственных векторов b_j. Векторы b_j аппроксимируют систему ортогональных на длительности импульса сигналов b_j(t), j = 1...M с точностью до шага дискретизации. Данную систему сигналов предлагается использовать для некогерентного приема СШП хаотических радиоимпульсов. Собственные значения λ_j матрицы B'B дают оценку вклада в энергию хаотического радиоимпульса каждого из b_j(t), j = 1...M сигналов [3, 4]. Поэтому, опираясь на распределение собственных значений, можно представить i-й хаотический радиоимпульс X_i длительности T_P линейной комбинацией не всех M базисных векторов, а только тех (M₀), что дают наибольший вклад в энергию импульса, т.е. , где β_ip проекция X_i на b_p.

В канале с одним лучом принимаемый хаотический радиоимпульс последовательно проецируется на каждый элемент базиса b_j, j = 1...M₀: результаты этих проекций возводятся в квадрат, суммируются и в итоге получается взвешенная оценка энергии хаотического радиоимпульса

,              (2)

с учетом того, что , если j ≠ p.

 

3. Многолучевое распространение

В канале с многолучевым распространением на входе приемника формируется сигнал

,                                              (3)

где x(t) – сигнал, излучаемый передатчиком (поток хаотических радиоимпульсов), y(t) – сигнал в точке приема после прохождения входных цепей приемника, n(t) – тепловой шум приемника, h(t) – функция-отклик канала, характеризующая многолучевое распространение,  – операция свёртки. Импульсный отклик h(t) канала определяется как отклик на δ-импульс: , которая формируется как сумма случайных слагаемых-лучей с амплитудой a_l и запаздыванием t_l, приходящих в точку приема [5].

При суммировании в точке приема переотраженных лучей, приходящих с задержкой, большей времени когерентности хаотического сигнала, суммирование хаотических колебаний происходит некогерентно, поэтому сумма лучей , попадающая в приемник, может быть представлена как сумма независимых некоррелированных хаотических сигналов  на амплитуды которых наложено ограничение , физически соответствующее полной мощности импульса, приходящей в точку приёма. Таким образом, на входе приемника формируется сигнал .

Оценку энергии i-го импульса можно получить как , где  и . Энергия, поступившая в приемник по всем лучам, составит:  и, в силу некоррелированности между собой коэффициентов , l = 0...L, j = 0...M₀, имеем

.                           (4)

Величина  является оценкой энергии радиоимпульса, пришедшего по l-му лучу. Таким образом, прием с помощью проецирования на базис из M₀ ортогональных сигналов в многолучевом канале дает взвешенную оценку суммарной энергии хаотических радиоимпульсов, приходящих по L лучам при условии некогерентного суммирования лучей точке приема.

Некогерентное сложение хаотических колебаний, приходящих с различными запаздываниями вытекает из автокорреляционных свойств хаотических сигналов. Здесь в качестве модели хаотического сигнала, используются колебания, полученные с помощью модели транзисторного генератора хаотических колебаний СВЧ диапазона [6].

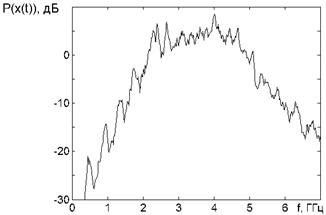
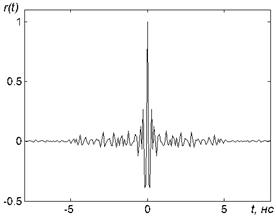
Спектр мощности хаотических колебаний, приведен на рис. 1a. На рис. 1b показана автокорреляционная функция потока хаотических радиоимпульсов, а на рис. 1c изображен фрагмент их реализации. Основная часть мощности колебаний генератора сосредоточена в полосе 2,2…5 ГГц. Из автокорреляционной функции следует, что время когерентности составляет ~0.35 нс и при суммировании в точке приема переотраженных лучей, приходящих с задержкой, которая больше времени когерентности, появляется реальная возможность осуществить в приемнике некогерентное суммирование хаотических колебаний и обработать каждый пришедший луч без потери энергии, вызываемой многолучевыми замираниями.

 

 

   

a)                                                        b)

 

c)

 

d)

 

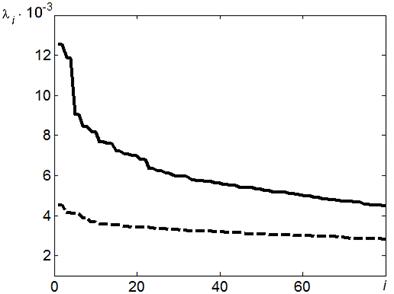
Рис 1. Система ортогональных сигналов для некогерентного приема сверхширокополосных
хаотических радиоимпульсов в многолучевом канале.

На рис. 1d показан результат вычислений спектра собственных значений ковариационной матрицы B'B, сформированной из хаотического сигнала. Сравнение этих распределений показывает, что для гауссовского шума нельзя выделить ограниченный набор базисных сигналов, которые вносят основной вклад в формирование колебаний [3].

 

4. Моделирование

         Апробация предложенного метода приема осуществлялась с помощью численного моделирования, согласно схеме на рис. 2.

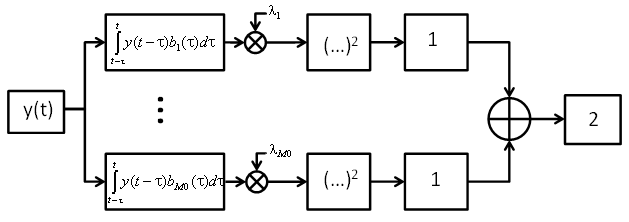
         Рис. 2. Система ортогональных сигналов для некогерентного приема сверхширокополосных
хаотических радиоимпульсов в многолучевом канале.

Согласно предлагаемому методу сигнал, поступающий из канала, в скользящем временном окне сворачивается с каждым из M₀ базисных сигналов. Далее результат свертки умножается на собственное значение, определяющее долю вклада данного базисного сигнала в энергию хаотического радиоимпульса, результат возводиться в квадрат, пропускается через фильтр нижних частот с полосой пропускания согласованной с длительностью хаотического радиоимпульса, и суммируется по всем ветвям. В итоге в каждый момент времени на выходе имеем взвешенную оценку энергии поступившего сигнала на длительности импульса. В моменты времени, когда на входе имеет место хаотический радиоимпульс, на выходе имеет место оценка энергии хаотического радиоимпульса. В отсутствии импульса на входе, на выходе формируется оценка энергии на пассивном интервале (между импульсами). Для принятия решения о приходе импульса или его отсутствии согласно рассматриваемому здесь методу передачи оценка энергии принятого импульса сравнивается с пороговым значением E_T: если она выше, то фиксируется приход радиоимпульса, если ниже, то фиксируется его отсутствие. Величина порогового значения E_T определялась по распределениям энергий сигнала на позиции импульса и позиций, на которых импульс отсутствовал, исходя из минимизации ошибок первого и второго рода.

 

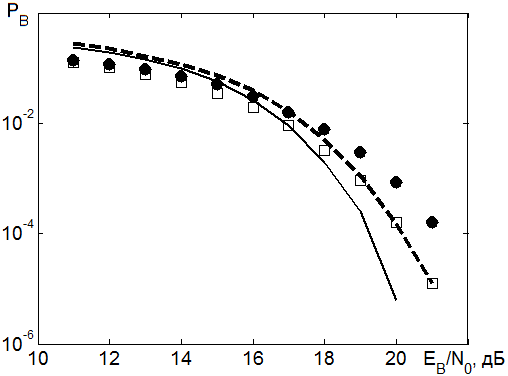
Рис. 3. Система ортогональных сигналов для некогерентного приема сверхширокополосных
хаотических радиоимпульсов в многолучевом канале.

В ходе моделирования была определена зависимость вероятности ошибки на бит P_B от отношения энергия на бит к спектральной плотности шума E_B/N₀ для энергетического и для предлагаемого метода приема (рис. 3). На рис. 3 изображена вероятность ошибки на бит P_B, для различных типов приема хаотических радиоимпульсов длительностью T_P = 40 нс. Размерность хаотического радиоимпульса (база сигнала) составляла M = 2ΔfT_P = 224, где Δf = 2,8 ГГц, T_P = 40 нс. Благодаря возможности выделить ограниченный набор базисных сигналов, размерность базиса, используемого для приема импульсов с помощью предложенного метода, составляла M₀ = 80.

5. Выводы

Полученные результаты показывают, что в канале с белым шумом и многолучевым распространением данный метод приема имеет практически те же вероятности ошибок на бит, что и энергетический прием. При этом некогерентный прием СШП хаотических радиоимпульсов осуществляется опираясь на совокупность признаков, которые остаются инвариантными относительно преобразования сигнала в канале.

Литература

1.     Дмитриев А.С., Ефремова Е.В., Лазарев В.А. et al // Успехи современной радиоэлектроники. 2013. №3. C.19.

2.     Андреев Ю.В., Дмитриев А.С., Лазарев В.А. // Успехи современной радиоэлектроники. 2013. №3. С.55.

3.     Кузьмин Л.В. // Успехи современной радиоэлектроники. 2013. №3. C. 90.

4.     Дмитриев А.С., Касьян Г.А., Кузьмин Л.В. // Изв. ВУЗов. Прикладная нелинейная динамика. 2003. № 3. C. 157.

5.     Channel Modeling Sub-committee Report Final. November 2002. IEEE P802.15 Working Group for Wireless Personal Area Networks (WPANs). // [Электронный ресурс]. URL:  http://grouper.ieee.org/groups/802/15/pub/2002/Nov02/02490r0P802-15_SG3a-Channel-Modeling-Subcommittee-Report-Final.zip

6.     Дмитриев А.С., Ефремова Е.В., Кузьмин Л.В. et al // Радиотехника и электроника. 2006. Т.51. В. 5. С. 593.