УДК 621.396.967
ИССЛЕДОВАНИЕ ВОЗМОЖНОСТЕЙ И ХАРАКТЕРИСТИК МЕТОДОВ СНИЖЕНИЯ УРОВНЯ ШУМА ПРИ ОБРАБОТКЕ СИГНАЛОВ, ОСНОВАННЫХ НА ПРИМЕНЕНИИ ВЕЙВЛЕТ-ТЕХНОЛОГИИ
В. О. Браун, В. П. Долгушин, В. Н. Лоза, И. В. Пампуха
Военный институт Киевского национального университета имени Тараса Шевченка
Статья получена 11 июля 2014 г.
Аннотация. В работе приведены результаты вычислительного эксперимента характеристик методов снижения уровня шумов (трешолдинга) при обработке сигналов на основе вейвлет-анализа. Приведены примеры применения трешолдинга для "очистки" от шума радиолокационных сигналов.
Ключевые слова: радиолокационные сигналы, шумоподавление, вейвлет-анализ, трешолдинг.
Abstract. The results of computing experiments of the methods for decreasing of radio interference level (tresholding) while processing of impulses based on wavelet analysis are represented in this paper. The examples of tresholding application for «clearance» from interference of radar impulses were given.
Key words: radar impulses, sound suppression, wavelet analysis, tresholding.
Формулировка задачи. Борьба с шумом считается поистине глобальной проблемой радиоэлектроники. При квазибелом шуме единственно реальным методом снижения уровня шума является высокочастотная фильтрация, но её возможности ограничены трудностью практической реализации требуемых частотных характеристик фильтров.
В настоящее время появился новый метод борьбы с шумом на основе алгоритмов развивающейся теории вейвлетов. Сущность метода снижения уровня шумов (по терминологии в литературе - "удаления" шума) при обработке сигналов по технологии вейвлет-анализа (ВА) заключается в программно-управляемой пороговой обработке детализирующих вейвлет-коэффициентов (ВК). Такой метод получил название трешолдинг (ТШ). По физической интерпретации, по мнению авторов, он также сводится к фильтрации высоких частот, но обладает принципиально новыми возможностями.
Главное преимущество метода ТШ заключается в широких возможностях вариации параметров обработки путём использования различных типов, способов пороговой обработки и их параметров.
Вейвлет-преобразование (ВВП) (декомпозиция) обладает свойством избыточности, при котором открывается возможность без потери информации "отсекать" частично или полностью ВК определённого уровня. Составляющие шума переносятся на высоких частотах и при ВА содержатся в детализирующих ВК нижних уровней декомпозиции сигнала. Самый интересный аспект метода ТШ заключается в том, что порог ограничения можно адаптивно изменять и устанавливать отдельно для каждого коэффициента.
Эффективность метода ТШ, кроме параметров обработки, зависит от вида сигнала и алгоритма ВВП. Наибольшая эффективность соответствует стационарным сигналам, для которых основная информация о сигнале содержится в аппроксимирующих и детализирующих ВК верхних уровней декомпозиции.
Имеющиеся в литературе по теории вейвлетов сведения по методу ТШ содержат информацию о принципах организации алгоритмов обработки, их прикладному программному обеспечению и некоторые примеры для тестовых сигналов, при этом читателю предлагается поэкспериментировать, меняя тип сигнала, уровень шума и параметры вычислительного алгоритма [1,2,3]. Без такого исследования нельзя ответить на целый ряд существенных для применения вопросов, возникающих при практическом использовании метода к решению конкретных задач радиоэлектроники. В частности, совершенно отсутствует информация о сравнении методов ТШ и выборе значений большинства параметров.
Это обстоятельство определило целевую направленность настоящей работы. Основной задачей является численное экспериментальное исследование влияния на эффективность шумоподавления многочисленных параметров метода ТШ и способов пороговой обработки, что способствует развитию теории ТШ и позволяет найти оптимальный набор параметров алгоритма ТШ.
В качестве основного критерия оценки принято относительное уменьшение стандартного отклонения (СО) шума (обозначение – std), кроме того приводятся оценки сравнения норм "очищенного" и исходного сигналов.
Вычислительные задачи решаются с помощью одного из лучших инструментальных средств по отработке вейвлет-технологии - пакета расширения Wavelet Toolbox компьютерной системы MATLAB – 2012B [3]. В работе приводятся только основные решающие функции алгоритма обработки. Предполагается, что читатель знаком с основами теории вейвлетов (изложенной, в частности в [1, 2, 4-8]).

Рис.1.
Перед анализом методов ТШ приводятся результаты вычисления порога (thr) при различных способах его определения в зависимости от уровня шума (рис. 1).
Решающая функция имеет вид:
thr = thselect (x, <способ>), (1)
где x - вектор сигнала (для примера – шума);
<способ> имеет следующие значения:
- rigrsure - адаптивный порог, использующий принцип Штейна [3] несмещённой оценки риска;
- heursure - эвристический вариант порога;
- sqtwolog - порог, равный sqrt(log (lengh(x));
- minimaxi - минимаксный порог (обозначены: sqrt - ![]() , length(x) – длина вектора x).
, length(x) – длина вектора x).
Исследование разновидностей метода ТШ производится в зависимости от алгоритма вейвлет-преобразования (ВВП) и способа установки порога при фиксированном сигнале. Для первых вариантов метода используется сигнал, относящийся к классу тестовых, который формируется встроенной функцией wnoise (.) или аналитическим выражением:
![]() + ksign(sin(x-b))),
(2)
+ ksign(sin(x-b))),
(2)
где a, b, k - числовые коэффициенты.
Исследование видов и параметров пороговой обработки вейвлет-коэффициентов.
Алгоритм ТШ-1. Дискретный алгоритм ВПП с порогом по стратегии Бирге-Массарта.
Алгоритм вейвлет-декомпозиции сигнала выполняется решающей функцией:
![]() ,
(3)
,
(3)
где c, l - коэффициенты разложения сигнала;
lev, W - уровень разложения и имя вейвлета.
Алгоритм пороговой обработки ВК использует стратегию Бирге-Массарт [6, 8], при которой выбирается значение thr, минимизирующее критерий штрафа, заданный формулой:
![]() (4)
(4)
где c(k) - вейвлет-коэффициенты в порядке убывания по абсолютному значению;
n - число коэффициентов пороговой обработки;
t* - точка минимума.
Операция вычисления порога имеет вид:
thr = wdcbm
(c, l,![]() ,
(5)
,
(5)
где ![]() -
параметр, определяемый числом в интервале [1, 10];
-
параметр, определяемый числом в интервале [1, 10];
m = 2* l(1).
Процедура удаления шума имеет три этапа: 1) разложение сигнала до заданного уровня в соответствии с (3); 2) определение порога, называемое детализацией, согласно (5); 3) реконструкция (восстановление) сигнала после пороговой обработки коэффициентов, выполняемое решающей функцией:
[sd, csd, lcd, p0,per] = wdencmp (‘lvd’, c, l, W, lev, thr, <вид порога>), (6)
где sd, csd, lsd - "очищенный" сигнал и коэффициенты восстановленного сигнала;
<вид порога> имеет одно из двух значений: "s" – мягкий и "h" – жёсткий (‘lvd‘ – необходимая опция);
p0, per - число ВК с пороговой обработкой в % и, так называемая, L2 -норма восстановления, равная отношению норм (иногда в квадрате) очищенного и исходного сигналов:
per = ![]() .
(7)
.
(7)
Иллюстрация видов порога приведена на рис. 2.

Рис. 2.
Алгоритм ТШ-2. Пакетная обработка. Глобальный порог.
Пакетный вейвлет-метод является обобщением ВВП и предлагает более широкий спектр функций анализа сигналов.
При пакетном ВА последовательная процедура разложения коэффициентов применяется не только к аппроксимирующим, но и детализирующим ВК. Для заданной ортогональной вейвлет-функции генерируется библиотека баз пакетных вейвлетов, которые используются для многочисленных разложений исходного сигнала.
Алгоритм пакетного ВА принято представлять "деревом" обработки, при этом результат обработки обозначается через T или чаще TREE. Иллюстрация "дерева" алгоритма для выбранного произвольно сигнала показана на рис. 3 (а – "дерево"; б – сигнал в узле (2,0)).

а. б.
Рис. 3.
Решающие процедуры – функции для пакетного ВВП (TREE), вычисления порога (thr) и реконструкции после пороговой обработки имеют следующий вид:
TREE = wpdec(s, lev, W), (8)
thr = wpbmpen(TREE, std, a), (9)
sd = wpdencmp(TREE, ‘s’, ‘nobest’, thr, 1), (10)
где ‘nobest’ - опция;
s - выбор мягкого порога (можно h).
Результаты вычислительного анализа алгоритмов ТШ-1 и 2 представлены ниже в виде графиков и таблиц.
На рис. 4 представлены зависимости стандартного отклонения результирующего шума (std(nd)): а) на верхнем - от уровня декомпозиции сигнала, б) на нижнем - от порядка вейвлета. Кривые 1 соответствуют пакетному алгоритму (алгоритм 2), кривые 2 - дискретному алгоритму ТШ-1. Исходными (до вариации параметров) выбраны значения: lev = 5, W = db4.
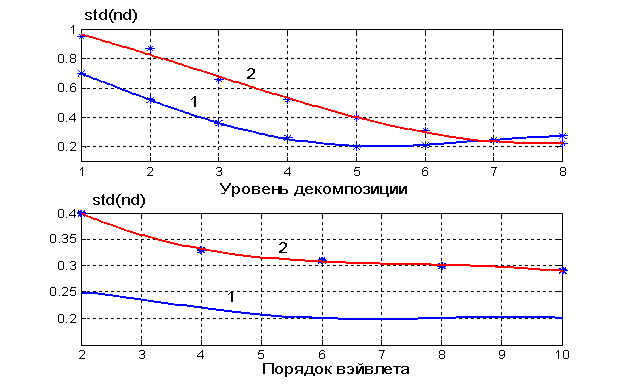
Рис. 4.
Анализ рис. 4 позволил сделать следующие выводы: 1) большая эффективность шумоподавления достигается при использовании алгоритма ТШ-2 с глобальным порогом; 2) зависимость от уровня декомпозиции показывает, что лучшие результаты соответствуют lev = 6; 3) порядок вейвлета слабо влияет на результаты ТШ, однако лучше применять вейвлеты с порядком, большим 5.
Для обоих обсуждаемых параметров существуют ограничения. Максимальное число уровней декомпозиции равно значению N - 1, где N - показатель размерности сигнала при двоичном исчислении L = 2N. Максимальное значение порядка зависит от типа вейвлета, так для выбранного базисного вейвлета Добеши он равен 10.
На следующем рис. 5 представлена зависимость СО результирующего шума от уровня исходного шума, заданного с помощью коэффициента g:
N = g*n0 при std(n0) = 1. (11)
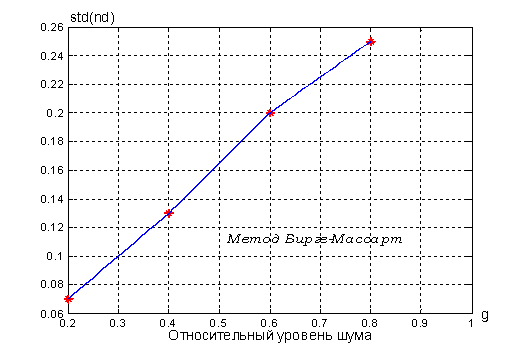
Рис. 5.
Как следует из рис. 5, уменьшение СО шума (алгоритм ТШ-1) при изменении g от 0,2 до 0,8 составляет в количестве раз величину от 2,85 до 3,2.
На рис. 6 представлены зависимости от уровня декомпозиции сигнала: слева - от отношения норм реконструированного и исходного сигналов (параметр "per" выражения (9)), справа - число "очищенных" коэффициентов за счёт пороговой обработки в %.

Рис. 6.
Для практики применения важным является факт восстановления формы сигнала после процедуры ТШ. Из рис. 6 (слева) следует, что соответствие норм полученного и исходного сигналов больше 0,9. Согласно рис. 6 (справа) при алгоритме ТШ-1 пороговой обработке подвергается более 50%, а при больших уровнях декомпозиции оно больше 90%.
Результаты влияния порогового параметра "а" на величину std(nd) приведены в таблице № 1 (для оптимальных величин lev и W).
Таблица 1
|
"а" |
1 |
2 |
3 |
4 |
5 |
|
std (nd) |
0,21 |
0,2 |
0,21 |
0,23 |
0,1995 |
В соответствии с данными таблицы 1 значение параметра "а" можно выбирать произвольно в интервале от 1до 5.
Алгоритм ТШ-3. Адаптивный порог.
Адаптивный порог задаётся путём выбора критерия оценки (обозначен R), в качестве которых используются пояснённые ранее: rigrsure, heursure, sqtwolog, minimaxi.
По имеющимся сведениям [1, 3], минимаксный и sure методы являются наиболее подходящими, когда малые составляющие сигнала находятся в полосе шума.
Решающая программная функция алгоритма имеет вид:
[sd, csd, lsd ] = wden (s, R, <вид порога >, SL, lev, W), (12)
где <вид порога> соответствует вставке ‘s’(мягкий) или ‘h’(твёрдый);
SL - строка, определяющая тип перемасштабирования шума, которое применяется в случае отклонения структуры шума от модели "белого" в интервале [0, 1]. Параметр имеет следующие текстовые значения:
- ‘one’ - без масштабирования;
- ‘sln‘ - перемасштабирование с использованием единственной оценки уровня шума на основании коэффициентов разложения первого уровня;
- ‘mln‘ - перемасштабирование с использованием оценок уровня шума, зависящих от уровня разложения.
Результаты исследования эффективности алгоритма ТШ-3 представлены графиками рис. 7 и 8, а также таблицы 2.
На рис. 7 показана зависимость СО результирующего шума от уровня декомпозиции для случаев без перемасштабирования и перемасштабирования по оценкам первого уровня.

Рис. 7.
Выводы из анализа: 1) применение перемасштабирования повышает эффективность алгоритма; 2) для обоих случаев можно выделить наилучшие уровни декомпозиции: при ‘one’ - lev = 6, при ‘sln’ - lev = 5; 3) количественные результаты по снижению уровня шума сравнимы с лучшими для алгоритмов ТШ-1 и 2, а при использовании перемасштабирования выше.
Рис. 8 показывает сравнение исходного и полученного в результате ТШ значений СО шума для всех трёх вариантов параметра перемасштабирования SL.
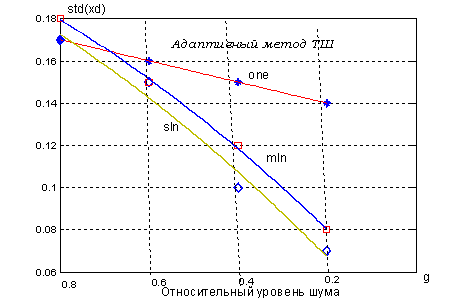
Рис. 8.
Выводы из анализа рис. 8: 1) адаптивный алгоритм ТШ даёт лучшие возможности шумоподавления по сравнению с алгоритмами ТШ-1 и 2 для "большого" уровня шума (для g = 0,8 выигрыш по СО составляет 4,4 … 4,7, а для ТШ-2 он соответствовал 3,2); 2) явно подчёркивается большая эффективность при использовании перемасштабирования, особенно при малых уровнях шума; 3) среди вариантов перемасштабирования рекомендуется ‘sln’.
Результаты исследования на качество шумоподавления критериев и видов порога представлены на рис. 9.
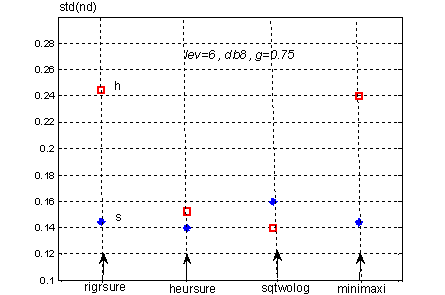
Рис. 9.
Виды порога обозначены различной формой маркёра. Для мягкого порога получены лучшие результаты при всех критериях, кроме sqtwolog. При мягком пороге выбор критерия почти не влияет на эффективность обработки. При жёстком пороге явно выражена оптимальность критериев sqtwolog и heursure. Исходные параметры построения графика показаны на рисунке, метод перемасштабирования - sln.
В таблице 2 для всех критериев и видов пороговой обработки адаптивного алгоритма ТШ приведены значения параметра, характеризующего степень отклонения "очищенного" сигнала от исходного без шума. Таким параметром служит квадрат нормы разности сигналов.
Таблица 2
|
Критерий |
rigrsure |
heursure |
sqtwolog |
minimaxi |
||||
|
Вид порога |
s |
h |
s |
h |
s |
h |
s |
h |
|
Norm2(s – sd) |
1.12 |
1.64 |
1.3 |
1.16 |
1.67 |
0.98 |
1.2 |
1.3 |
Как следует из таблицы 2, лучшие показатели имеет универсальный критерий (sqtwolog) с жёстким порогом (выделено в таблице).
Дополнительно исследована зависимость результатов шумоподавления от выбора уровня детализирующих ВК для оценки шума, используемой при вычислении порога в (5) - таблица 3.
Таблица 3
|
m = n*l(k) |
k |
l(k) |
2*l(k) |
|
1 |
0,25 |
0,32 |
|
|
2 |
0,26 |
0,33 |
|
|
3 |
0,3 |
0,36 |
Из таблицы следует, что лучшим является выбор m = l(1).
Алгоритм ТШ с использованием функции выбора параметров по умолчанию.
В теории ТШ предусмотрена возможность определить параметры обработки по умолчанию с помощью программной функции:
[thr, sorh, crit] = ddencmp(‘den’,’wv’, sn), (13)
где crit - имя предлагаемой энтропии;
‘den’ ‘wv’ - опции, определённые для режима удаления шума.
Применение функции (13) для использованного в предыдущих вычислениях сигнала с шумом и параметрах lev w, соответствующих оптимальным согласно предыдущих выводов (6 и db8), даёт следующие результаты:
thr = 3,75, sorh = ‘s’, crit = ‘shannon’.
Выполнение алгоритма ТШ в соответствии с выражением (10) при данных параметрах позволяет снизить уровень шума до значения СО, равного 0,218.
При использовании алгоритма глобального порога по выражению (9) получаем:
thr = 3,35 и std(nd) = 0,215.
Результат вычисления позволяет сделать вывод о равноценном с другими алгоритмами определение порога по выражению (13).
Результаты проведенного вычислительного анализа представляют достаточно большой набор новых данных о влиянии параметров алгоритма ТШ на эффективность шумоподавления, как в плане качественных выводов, так и их количественной оценки. В то же время степень сохранения формы исходного сигнала наиболее наглядно демонстрируется визуальным методом сравнения исходного образца с полученным после применения ТШ.
Примеры такого представления для двух используемых при анализе тестовых сигналов приведены на рис. 10, где использованы обозначения: S - исходный сигнал, SN - сигнал с шумом, SD - сигнал, реконструированный после применения алгоритма ТШ.
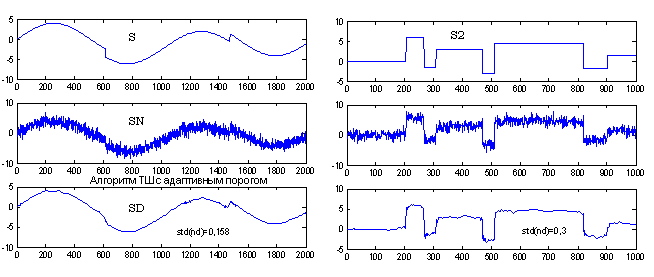
Рис. 10.
Применение методов трешолдинга при обработке радиолокационных сигналов.
Существующие в известной авторам литературе примеры применения методов ТШ, кроме тестовых сигналов, ограничиваются сигналами звуковых колебаний и электрокардиограммы.
В статье рассматриваются примеры применения алгоритмов ТШ для двух случаев обработки сигналов в радиотехнических системах.
1. Системы обработки и измерения временных параметров импульсных сигналов (простой импульс и ЛЧМИ).
Примеры результатов вычислительного анализа представлены на рис. 11 и 12.
Снижение СО шума от исходного значения 0,8 до полученного после реконструкции 0,185 (уменьшение в 4,32 раза) обеспечивает уменьшение потенциальных ошибок временных измерений, а для ЛЧМИ повышает качество сжатия сигнала.
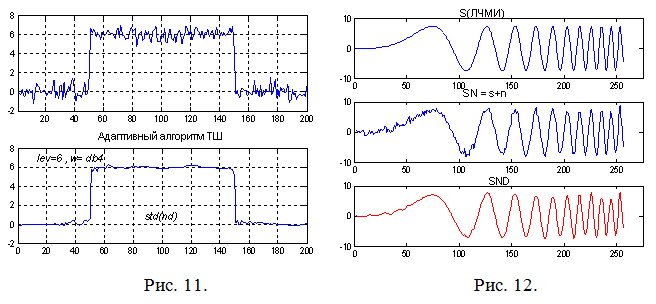
2. Повышение качества распознавания формы сигнала при вейвлет-технологии обработки.
Вейвлет-анализ даёт уникальные возможности распознавания локальных и "тонких" особенностей сигналов, что обеспечивает его применение для распознавания флюктуаций сигнала, имеющее место при радиолокации групповых сосредоточенных целей (возможности метода рассмотрены в авторской работе [9]).
Особенности применения методов ТШ для сигналов сложной формы с наличием локальных перепадов заключается в том, что информация о скачках функции, как и шума, сосредоточена в нижних уровнях детализации, поэтому применение метода требует тщательного подбора параметров алгоритма ТШ и контроля качества сохранения структуры сигнала путём оценки L2-нормы реконструированного сигнала и средств визуального контроля. Наиболее информативным является визуализация на основе спектрограмм (СПГ) результирующего сигнала.
Для анализа использована модель огибающей пачки с двумя всплесками и двумя провалами до уровней 0,7 и 0,5. Модель сигнала без шума (слева) и соответствующая ему спектрограмма результата ВВП (справа) показана на рис. 13.
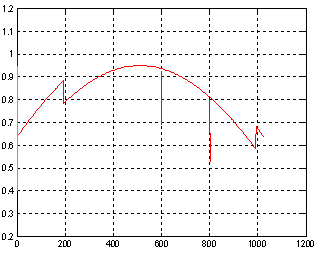

Рис. 13.
Спектрограмма позволяет чётко определить все флюктуации (более ярко показаны области провалов) и их положение на временной оси.
Результаты обработки в присутствии шума показаны на рис. 14: слева - модель сигнала, в центре - СПГ без применения ТШ, но с ограниченным уровнем шума (std(n)=0.7), справа - СПГ после применения ТШ и реконструкции сигнала.
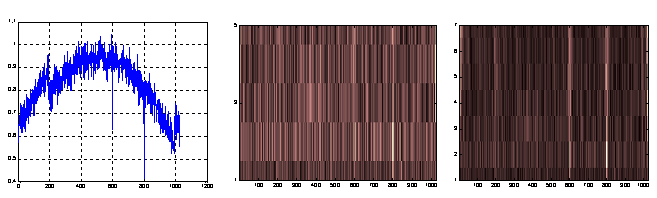
Рис. 14.
Из анализа рис. 14 следует, что наличие шума даже несколько меньше стандартного практически не позволяет по СПГ достоверно обнаружить наличие флюктуаций в модели сигнала. Применение ТШ позволяет уменьшить уровень шума в 4 ... 5 раз, и СПГ в принципе позволяет различить наличие и положение локальных флюктуаций, при этом лучше подчёркиваются провалы в огибающей.
Заключение. Активно развивающиеся методы прикладной математики по новой теории альтернативного спектрального анализа с помощью базиса "малых" волновых функций и процедуры кратномасштабного анализа позволяют существенно расширить инструментальную базу информационных технологий обработки сигнала.
Благодаря новаторской работе Д.Л. Донохоу [10] для некоторых шумовых моделей созданы алгоритмы очистки от шума и в общем виде сформулированы рекомендации по выбору порогового уровня обработки детализирующих коэффициентов, позволяющих снизить уровень шума, не нарушая важных особенностей сигнала. В основе очистки от шума, а также сжатия сигналов (последнее в работе не рассматривается) лежат основные свойства кратномасштабного анализа и возможность локализации энергии при дискретном ВВП.
Экспериментальные результаты, полученные в статье, дают количественную характеристику эффективности методов трешолдинга в зависимости от способов, видов пороговой обработки и конкретных параметров. Рассмотрены вопросы применения методов ВА с использованием трешолдинга для нескольких моделей сигналов радиолокационных систем обнаружения.
Литература
1. Смоленцев Н.К. Вейвлет-анализ в MATLAB – М.: ДМК Пресс, 2010. – 448 с.
2. Воробьёв В.И., Грибунин В.Г. Теория и практика вейвлет-преобразования. СПб.:Изд-во ВУС, 1999. – 204 с.
3. Дьяконов В.П. MATLAB и SIMULINK для радиоинженеров. – М.: ДМК Пресс, 2011. – 976 с.
4. Добеши И. Десять лекций по вэейвлетам. - Ижевск НИЦ "Регулярная и хаотическая динамика", 2001. – 464с.
5. Бурнаев Е.В. Применение вейвлет-преобразования для анализа сигналов. – М.:МФТИ, 2007. – 138 с.
6. Малла С. Вэйвлеты в обработке сигналов – М.: Мир, 2005. – 671 с.
7. Чуи К. Справочник по вероятностным расчётам – М.: Воениздат, 1970. – 468с.
8. Новиков И.Я., Стечкин С.Б. Основы теории всплесков. Успехи математических наук, 1998, т.53, №6, с. 53-128.
9. Долгушин В.П., Лоза В.Н., Борзак А.Н., Жиров Б.Г. Распознавание класса целей методом оценки статистических параметров вектора вейвлет-декомпозиции сигнала // Сборник научных трудов Военного института Киевского национального университета имени Тараса Шевченка №45, 2014, с. 24 – 33.
10. D.L. Donoho. Denoising by Soft – Threshokling. IEEE Transactions on Information Theory, 1995. – p. 613-627.