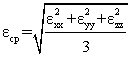Исследование эффективности численных методов и программ компьютерного моделирования в процессе проектирования микрополосковых фильтров СВЧ.

Исследование эффективности численных методов и программ компьютерного моделирования в процессе проектирования микрополосковых фильтров СВЧ

Д. В. Денисенко, В. В. Радченко

ФГУП «ЦНИРТИ им. академика А.И. Берга», Москва, Россия

Статья получена 12 июля 2014 г.

Аннотация. Рассмотрены достоинства и недостатки численных методов квазистатического и электромагнитного моделирования, применяемых в процессе разработки планарных СВЧ устройств. Проведен сравнительный анализ результатов численного моделирования и измерения характеристик конструктивно различных микрополосковых фильтров СВЧ в диапазоне от 1 до 18 ГГц. По результатам исследования предложены практические рекомендации для повышения достоверности моделирования характеристик микрополосковых СВЧ фильтров и других планарных устройств. Выявлены анизотропные свойства диэлектрической проницаемости поликоровых подложек и оценен ее разброс.

Ключевые слова: микрополосковые фильтры, планарные СВЧ устройства, электромагнитное моделирование, метод конечных элементов, метод моментов.

Abstract: The advantages and disadvantages of the numerical methods of quasi-static and electromagnetic simulation, applied in the process of the planar microwave devices designing are examined. The comparative analysis of results of numerical simulation and measurement characteristics of constructively different microstrip filters in the range from 1 to 18 GHz is made. According to research, practical recommendations to improve the reliability modeling of the characteristics of microstrip filters and other planar devices are proposed. Identified anisotropic properties of dielectric permittivity Al2O3 ceramic substrates are estimated.

Keywords: microstrip filters, planar microwave devices, electromagnetic simulation, numerical methods, finite elements method, method of moments.

Введение

Программы численного моделирования находят широкое применение в проектировании планарных СВЧ устройств. Они позволяют существенно сократить время разработки технически сложных устройств, оптимизировать их характеристики, а также своевременно находить ошибки проектирования, что позволяет сократить объемы макетирования и финансовые затраты. В настоящее время существует большое количество коммерческих программ, пригодных для моделирования характеристик планарных СВЧ устройств. В них реализованы различные электродинамические и квазистатические численные методы с применением, как строгих постановок электродинамических задач, так и приближенных, основанных на различных упрощениях модели реального устройства, что в свою очередь сказывается на результатах моделирования и в ряде случаев может приводить к неверным результатам. Для успешного использования программ численного моделирования, пользователю следует понимать технические особенности и ограничения численных методов, которые в этих программах реализованы, а также учитывать конструктивные особенности рассчитываемых устройств.

Теория

Методы численного моделирования планарных устройств можно разделить на квазистатические и электромагнитные (рис.1). Квазистатические методы являются модификацией метода теории цепей, в которой планарные линии передачи и неоднородности описываются в виде функциональных зависимостей элементов матриц рассеяния, определенных на основе телеграфных уравнений. Таким образом, комплексная исходная задача заменяется композицией из многополюсников, которые моделируют характеристику передачи составных частей устройства: линий передач, связанных линий, неоднородностей и др. Эти объекты рассматриваются в 2д сечениях и предполагается, что в них распространяются квази-Т-волны. Декомпозиция устройства осуществляется пользователем вручную, что может привести к ошибкам, а достоверность метода зависит от используемых в моделях приближений.

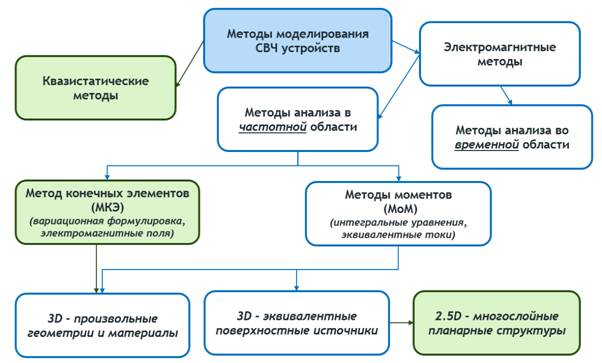
Рис.1 Классификация методов

Такой подход обеспечивает в ряде случаев достаточно высокую для практических задач точность, однако не все реальные устройства поддаются декомпозиции на элементы и не все физические эффекты можно учесть таким образом [1]. В большинстве практических ситуаций квазистатические методы позволяют обеспечить приемлемое совпадение результатов расчетов и экспериментов и являются незаменимыми на этапе синтеза и параметрической оптимизации устройств в связи с их высоким быстродействием.

Электромагнитные методы основаны на постановке граничной задачи для электромагнитных полей в трехмерном пространстве. Решение сводится либо к поиску экстремума функционала, который получается в вариационной формулировке для дифференциальных уравнений (ДУ) Гельмгольца относительно электромагнитных полей, либо к интегральным уравнениям (ИУ) относительно неизвестных плотностей токов в однородной области. Полученные операторные уравнения решаются проекционно-сеточными методами путем дискретизации пространства на конечные элементы. Неизвестные функции заменяются линейной комбинацией базисных функций, затем процедурой тестирования получившееся уравнение сводится к эквивалентной системе линейных алгебраических уравнений (СЛАУ). Наиболее известны такие методы решения линейных операторных уравнений, как метод Галеркина и коллокаций. Они являются частными случаями более общих методов моментов и различаются набором базисных и тестовых функций. В электродинамике применение метода Галеркина к решению ДУ в частотной области известно, как метод конечных элементов (МКЭ), а к решению ИУ - метод моментов (МоМ).

В основе МКЭ [2] лежит векторное уравнение Гельмгольца для одного из полей:

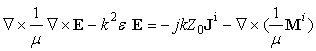где - импеданс материала, Jⁱ и Mⁱ - известные источники возбуждения электрического и магнитного токов, . Анализируемый объем дискретизируется на конечные элементы, чаще всего на тетраэдры, в пределах которых параметры материала неизменны, но могут свободно меняться от элемента к элементу.

При составлении интегральных операторов в МоМ используется понятие функции Грина (ФГ), которая в ряде случаев может быть вычислена аналитически [2]. ФГ связывает точку источника r' c точкой наблюдения r и является решением неоднородного уравнения Гельмгольца с дельта-функцией в качестве источника

Решение аналогичного уравнения с произвольным источником находится как скалярное произведение функции распределения источника и ФГ.

Таким образом, поля или потенциалы выражаются через эквивалентные распределения токов на поверхностях или в объемах неоднородностей, после чего составляются ИУ относительно неизвестного распределения токов на основе граничных условий. Стоит отметить, что однородные изотропные тела могут быть представлены эквивалентным распределением токов на их поверхностях [4], что избавляет от необходимости разбивать на конечные элементы весь объем и позволяет существенно сократить количество неизвестных СЛАУ. Такие методы называются методами граничных элементов (МГЭ).

Среди множества модификаций МоМ широко распространены 2.5D методы, которые предназначены для численного анализа плоскопараллельных многослойных планарных структур. В основе таких методов лежит декомпозиция 3D задачи на две 2D задачи в вертикальном и горизонтальном сечениях рассматриваемой модели [5], что позволяет значительно сократить машинное время. Слои диэлектриков представляются в виде эквивалентной схемы, составленной из линий передачи длиной в толщину слоя. Токи и напряжения в таких линиях описываются телеграфными уравнениями, что справедливо для слоев, сравнительно тонких по отношению к длине волны. Бесконечно тонкие проводники располагаются на границах между слоями диэлектрика. В формулировке метода они заменяются эквивалентным распределением электрических токов, и задача сводится к возбуждению некоторой схемы источниками токов на границах между слоями.

Для составления ИУ используется граничное условие для тангенциальной компоненты электрического поля на поверхности проводника:

n×(E^scat + E^inc)=Z_sJ_s,

где Z_s- поверхностный импеданс проводника, J_s - плотность электрического тока, E^inc‑падающее поле, E^scat - рассеянное поле, которое может быть выражено через распределение плотности тока и x-y компоненты ФГ.

Таким образом, в 2.5D MoM дискретизации пространства подвергаются поверхности проводников, а токи возможны только в горизонтальных направлениях на границах между слоями и в вертикальном направлении в слоях, что позволяет дополнять модель вертикальными перемычками. Преимущества и недостатки методов электромагнитного и квазистатического моделирования приведены в таблице 1.

Таблица 1. Сравнение методов моделирования планарных СВЧ устройств
	Квазистатические	МКЭ	МоМ 3D	МоМ 2.5D
Достоинства	Очень высокая скорость вычислений	Произвольные материалы и геометрии Строгая постановка задачи Разреженная матрица СЛАУ ленточной структуры Быстрое заполнение матрицы	Строгая постановка задачи Разнообразие модификаций метода Простота дискретизации поверхностей Дискретизация только области неоднородностей	Высокая скорость вычислений Дискретизация только поверхностей проводников
Недостатки	Сильное упрощение модели Низкая достоверность результатов	Сложность дискретизации объема Большие затраты машинного времени	Плотная матрица СЛАУ, долгое заполнение матрицы, сложность вычисления диагональных и близлежащих элементов	Невозможность моделирования произвольных 3Д объектов
Особенности	Декомпозиция устройства осуществляется пользователем вручную	Область расчета должна быть ограничена Дискретизируется вся моделируемая область Сложность O(N²)	Высокая чувствительность к дискретизации Неограниченное пространство Сложность O(N³) (обращение матрицы) Заполнение матрицы O(N²)	Отсутствие горизонтальных токов между слоями
Примеры программ	AWR DE, Nexxim	HFSS, Comsol Multiphysics, Agilent EMPro	FEKO, Efield, EMAP5	Ansys Designer, Agilent Momentum, AWR EMSight

Объекты исследований

Для исследования эффективности численных методов компьютерного моделирования планарных устройств нами был отобран ряд микрополосковых фильтров в диапазоне от 1 до 18 ГГц на поликоровых подложках толщиной от 1 мм до 0,25 мм.

Выбор микрополосковых СВЧ фильтров в качестве объекта исследований обусловлен тем, что они представляют собой сложную конструкцию из связанных планарных резонаторов, которая чувствительна к малым изменениям геометрических размеров и параметров материалов.

Рис.2 Исследуемые фильтры

Таблица 2. Конструкции исследуемых фильтров
Конструкция фильтра	Диапазон частот, ГГц	Полоса частот, %	Толщина подложки, мм	Особенности конструкции
Лестничный	10 … 30	10 … 67	0,5 0,25	Малые зазоры между резонаторами
Шпилечный	8 … 18	3 … 15	0,5	Малые зазоры между резонаторами
Встречно-стержневой	0,5 … 12	5 … 50	1,0 .. 0,5	Сквозные металлизированные отверстия
На заземленных четвертьволновых отрезках резонаторов	2 … 18	40 … 67	0,5	Сквозные металлизированные отверстия
ФНЧ	1 … 30	От постоянного тока до частоты среза	0,5 … 0,25	Планарные резонаторы, соединенные тонкими проводниками

Это усложняет численное моделирование данного класса устройств и требует более детального учета параметров материалов. Конструкции исследуемых фильтров приведены в таблице 2, а внешний вид фильтров представлен на рис.2.

В процессе исследования характеристики фильтров измерялись в специальном контактном устройстве спектральным анализатором цепей Agilent. Для оценки влияния контактного устройства в нем были измерены полоски длиной 5 мм и 10 мм, а затем из измеренных матриц S‑параметров фильтров вычиталась полученная матрица рассеяния контактного устройства с контрольными полосками.

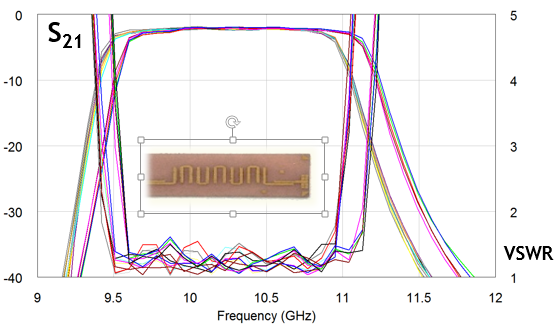
На рис.3 представлены результаты измерений 12 одинаковых фильтров, изготовленных на двух различных партиях подложек из поликора толщиной 0.5мм и ДП ε = 9,7 ± 0,25 по документации. Разброс параметров подложек более ярко выражен по сравнению с технологическим и укладывается в допуск. В численном расчете разброс ДП тоже укладывается в допуск, но центральные частоты фильтров существенно смещена вверх.

Рис.3 Технологический разброс и разброс параметров поликоровых подложек толщиной 0.5мм на примере шпилечного фильтра

Сравнение результатов измерений и моделирования

Численные расчеты фильтров проводились методами МоМ 2.5D и МКЭ. На результаты моделирования фильтров помимо геометрических размеров топологии, влияние оказывают толщина проводников, толщина и диэлектрическая проницаемость поликоровой подложки, наличие экрана. Каждым методом фильтры моделировались в приближении с бесконечно тонкими микрополосковыми проводниками, которые используются по умолчанию в 2.5D МоМ, так и с проводниками конечной толщины T=10 мкм. В приближении бесконечно тонких проводников не полностью учитывается связь между резонаторами, что приводит к более узкой полосе частот и сдвигу центральной частоты вниз. Это влияние тем больше, чем меньше расстояние между проводниками и чем выше частота. Кроме того, в такой модели потери завышаются, что дополнительно сужает ширину полосы фильтров [6].

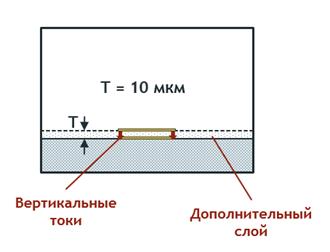
В МКЭ с учетом толщины проводников трудностей не возникает, задаются физические размеры проводников. В 2.5Д МоМ толщину проводника можно моделировать путем введения дополнительных тонких слоев с вертикальными перемычками между проводниками (рис.4). При таком подходе результаты МоМ получаются близкими к результатам МКЭ ценой сильно увеличенного времени расчета.

Рис.4 Проводник конечной толщины в 2.5D модели

В качестве эталонного метода использовался векторный МКЭ с большим количеством элементов, построенных методом адаптивных сеток, который позволяет эффективно разбивать область расчета на более мелкие элементы в местах сильного изменения поля. Для высокой точности расчета фильтров требуется достаточно много элементов, поэтому в целях улучшения сходимости использовались базисные функции 2-го порядка. На рис.5 приведены расчеты S₂₁ шпилечного фильтра в зависимости от количества тетраэдров. С увеличением количества тетраэдров решение стабильно приближается к точному решению: центральная частота сдвигается вверх, а ширина полосы сужается. Для исследуемых фильтров, при увеличении количества тетраэдров выше 300 тыс. дальнейшего прироста точности не наблюдалось.

Рис.5 Зависимость решения МКЭ от количества тетраэдров

Сравнения результатов расчета МКЭ и МоМ 2.5D показывают, что при достаточно высокой точности расчета, оба численных метода дают аналогичные результаты для одинаковых моделей. Различия же расчетных и измеренных характеристик существенны (рис. 6, рис. 7).


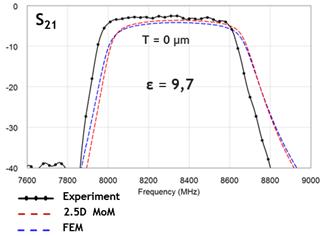
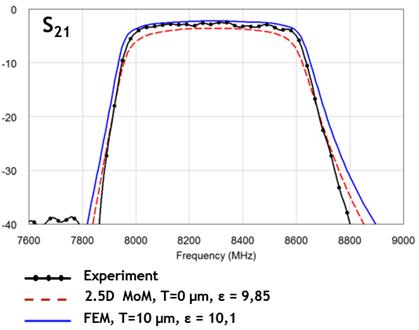
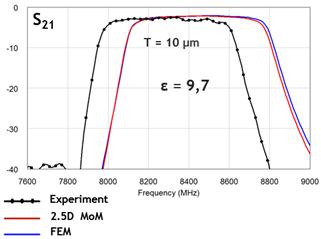
Рис.6. Результаты измерений и расчета модели с бесконечно тонкими проводниками.	Рис.7. Результаты измерений и расчета модели с проводниками конечной толщины.

Совпадения центральной частоты расчетных и измеренных характеристик (рис. 8) можно добиться путем выбора значения ДП подложки, однако при этом не получится обеспечить совпадение по ширине полосы пропускания. а выбранные значения ДП ε_ср = 9,85 в модели с бесконечно тонкими проводниками и ε_ср = 10,1 для модели с проводниками конечной толщины для рассматриваемых фильтров, выходят за границы допуска ДП по документации ε = 9,7 ± 0,25. Отметим, что верхняя граница допуска составляет ε_ср = 9,95.

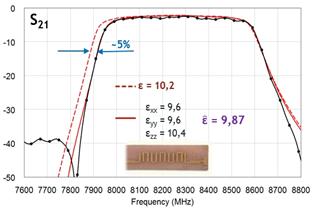
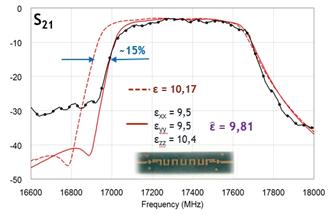
Рис.8 Измеренные и расчетные характеристики в результате подбора ДП.

Для полного совпадения результатов расчета и эксперимента необходимо задать для ДП подложек анизотропные свойства. На рис.9 пунктиром указан расчет без учета анизотропии, сплошной – с учетом, для различных фильтров. Вертикальная составляющая ДП ε_zz почти на 1 больше горизонтальных ε_xx, ε_yy, при этом среднеквадратичное значение укладывается в допуск. Это объясняется тем, что керамические зерна, из которых состоит подложка, имеют не правильную сферическую форму, а вытянутую и при изготовлении выстраиваются определенным образом [7].

Метод измерения ДП подложек, используемый для контроля в процессе производства, позволяет измерить только средние значения ДП без учета анизотропных свойств. Анализ различных конструкций фильтров, изготовленных на разных партиях подложек, позволяет приближенно оценить разброс компонент тензора, при которых получается совпадение расчета и измерений.

Рис.9 Измеренные и расчетные характеристики с учетом анизотропии и без.

Пунктир – расчет МКЭ без учета анизотропии ДП, сплошная линия – расчет МКЭ с учетом анизотропии ДП, сплошная с точками – измерения.

По результатам исследований проведена оценка разброса составляющих диэлектрической проницаемости поликоровых подложек. Значения ДП поликоровых подложек, определенные по результатам исследований, приведены в таблице 3.

Заключение

В большинстве случаев МКЭ обеспечивает более высокую точность моделирования по сравнению с другими методами и является наиболее предпочтительным на заключительных этапах проектирования. При моделировании методами MoM 2.5D для повышения точности следует самостоятельно задавать проводники в виде нескольких слоев, соединенных между собой вертикальными перемычками.

Таблица 3. Параметры поликоровых подложек 1 мм и 0,5 мм
	По документации	По результатам исследований
Толщина, мм	1,00_-0,06	0,97
Толщина, мм	0,5_-_0,04	0,48
Диэлектрическая проницаемость в диапазоне частот 8 – 10 ГГц	9,7 ± 0,25	ε_xx₍_yy₎= 9,35± 0,25 ε_zz = 10,35± 0,25 ε_ср = 9,7± 0,25*
Тангенс угла диэлектрических потерь	Не более 1∙10^-4	2∙10^-4
*, где ε_xx_, ε_yy_, ε_zz - компоненты тензора ДП.

В результате исследования установлено, что диэлектрическая проницаемость поликоровых подложек имеет явно выраженные анизотропные свойства и это следует учитывать для корректного численного моделирования планарных СВЧ устройств, отдавая предпочтение программам, в которых можно задать анизотропные свойства диэлектриков.

Литература

1. В. В. Радченко, Исследование методов повышения точности электростатического моделирования пассивных СВЧ устройств на основе планарных структур. // Сборник научных трудов ФГУП «ЦНИРТИ им. академика А.И.Берга».2011г.- ч .2,- с.76-98

2. Volakis J. L., Chattejee A., Kempel L. C. Finite Element Method for Electromagnetics: Antennas. Microwave Circuits, and Scattering Applications/ Piscataway, NJ: Wiley IEEE Press Series on Electromagnetic Wave Theory, 1998, 343 p.

3. Tai Chen-To, Dyadic green functions in electromagnetic theory/ IEEE Press, Piscat- away, NJ, 1994, 343 p.

4. B.M. Kolundzĳa and A.R. Djordjevic. Electromagnetic Modeling of Composite Metallic and Dielectric Structures. Artech House, 2002, 408 p.

5. J.R. Mosig, "Arbitrarily shaped microstrip structures and their analysis with a mixed potential integral equation", IEEE Trans. Microwave Theory Tech., MTT- 36, No. 2, 1988, pp. 314-323.

6. Радченко В.В Электромагнитное моделирование СВЧ устройств на основе базисных функций высшего порядка // Материалы 21-й Международной Крымской конференции. –Севастополь, 2012, с. 135-137

7. Dankov, P.I., “Dielectric anisotropy of modern microwave substrates,” in ... Devices to Antenna and Applications, Rijeka, Croatia: InTech, 2010, Chap. 4, pp.75-101.