Метод расчета постоянной распространения вытекающей моды в волноводах со щелями

Метод расчета постоянной распространения вытекающей моды в волноводах со щелями

В. И. Калиничев ¹, А. А. Бабаскин ²

¹ИРЭ им. В. А. Котельникова РАН²RF Mtech, Сеул, Юж. Корея

Статья получена 24 июня 2015 г.

Аннотация. Предложен и апробирован метод расчета комплексной постоянной распространения вытекающей моды в волноводах со щелями. Метод основан на сведении к задаче на собственные значения в эквивалентном резонаторе. В качестве примера рассмотрены одномерная и двумерная решетки излучателей в виде круглых отверстий в стенке прямоугольного и планарного волноводов. Приведено сравнение с аналитическим методом Олинера. Предложенный в работе метод может служить для моделирования и проектирования антенн вытекающей волны.

Ключевые слова: волноводы со щелями, вытекающая мода, постоянная распространения, эквивалентный резонатор, собственные колебания, антенны вытекающей волны.

Abstract. A method of calculating the complex propagation constant of a leaky mode in slotted waveguides is proposed and approved. The method is based on reduction to the problem of eigenmodes in the equivalent resonator. One-dimensional and two-dimensional arrays of slots in the form of circular holes in the wall of rectangular and planar waveguides are considered as an example. A comparison with the Oliner’s analytical method is given. The proposed method can be used for the modeling and design of leaky-wave antennas.

Key words: slotted waveguides, leaky mode, propagation constant, equivalent resonator, eigen modes, leaky-wave antennas.

Введение

Антенные решетки на основе волноводов со щелями применяют в СВЧ устройствах, в которых требуется частотное сканирование луча или многолучевой режим работы. В частности, такие решетки используются в квазиоптических интегральных схемах миллиметрового диапазона, см. например, [1-3], а также в устройствах пассивного радиовидения [4]. Антенные решетки этого типа относятся к более широкому классу антенн вытекающей волны, теория и проектирование которых изложены в ряде основополагающих зарубежных и отечественных работ, в частности, [5-7] и [8-11]. Обзор по антеннам вытекающей волны, включая однородные и периодические структуры с излучением, и методам их исследования представлен в [12]. Дальнейшее развитие методов расчета и инженерного проектирования широкого класса антенн с последовательным питанием, включая антенны бегущей волны, содержится в [13]. Там же приводится обширная литература по анализу и проектированию антенн данного класса.

Постоянная распространения излучающей моды является важной характеристикой антенн вытекающей волны. Для ее расчета можно использовать метод интегральных уравнений, см., например, [10-11]. Однако строгие аналитические методы связаны со сложным математическим анализом и трудоемкими вычислениями. Поэтому применяют также приближенные аналитические методы. Примером являются вариационный метод и метод поперечного резонанса [5, 7]. Следует отметить, что аналитические методы, в основном, рассматривают модели с нулевой толщиной металлизации и металлических стенок и не могут быть легко обобщены на случай их конечной толщины. Несмотря на существование аналитических методов, разработка эффективных численных методов расчета постоянной распространения для анализа и проектирования антенн вытекающей волны остается актуальной задачей. Одним из положений теории антенн вытекающих волн является то, что знание комплексной постоянной распространения в зависимости от параметров структуры позволяет проектировать антенны с заданным амплитудно-фазовым распределением вдоль излучающей апертуры [7, 12]. С развитием программ электромагнитного моделирования возникают и новые возможности для решения этих задач. В статье [14] предложен подход, позволяющий свести задачу о постоянной распространения в периодических структурах к собственной частоте эквивалентного резонатора. Там же с помощью программы электромагнитного моделирования этот метод продемонстрирован на примере расчета комплексной постоянной распространения в закрытом волноводе с периодически расположенными диэлектрическими вставками. Также отмечается возможность применения данного метода и для структур с излучением, однако примеры решения и результаты для волноводов с вытекающими модами не представлены. Цель работы – предложить и апробировать численный метод расчета комплексной постоянной распространения вытекающих мод в щелевых волноводах на основе программы электромагнитного моделирования, использующей метод конечных элементов. Одним из достоинств данного метода является то, что в отличие от аналитических методов он не требует специального рассмотрения для случая конечной толщины металлических стенок, в которых прорезаны щели, или конечной толщины металлизации. Насколько известно авторам, этот метод ранее не был описан в литературе.

Метод решения

Идея метода состоит в том, чтобы использовать программу электромагнитного моделирования HFSS [15] в режиме расчета собственных значений (eigen modes) для нахождения постоянной распространения вытекающей моды в периодических прямоугольных и плоских волноводах со щелями, через которые происходит излучение при использовании таких структур в антеннах вытекающей волны. Обычно режим eigen modes используется для расчета собственных частот закрытых резонаторов без излучения. В данной работе предложено использовать его для расчета комплексной постоянной распространения в структурах с вытекающими волнами.

Одномерная решетка в прямоугольном волноводе

В качестве примера рассмотрим прямоугольный полый волновод сечением 10.16х22.86 мм с линейной решеткой круглых отверстий диаметром 7.94 мм в узкой стенке, расположенных с периодом p = 12.7 мм, см. рис.1а [5]. Критическая частота основной ТЕ₁₀моды 6.56 ГГц. (В [5] размеры указаны в дюймах, здесь они пересчитаны в миллиметры). Стенки волновода предполагаются бесконечно тонкими и идеально проводящими. Выбор этой структуры в данной работе обусловлен возможностью сравнить результаты численного расчета для постоянной распространения с приближенным аналитическим решением на основе метода поперечного резонанса [5, 7]. Для расчета комплексной постоянной распространения в таком волноводе предложена модель, показанная на рис. 1б.

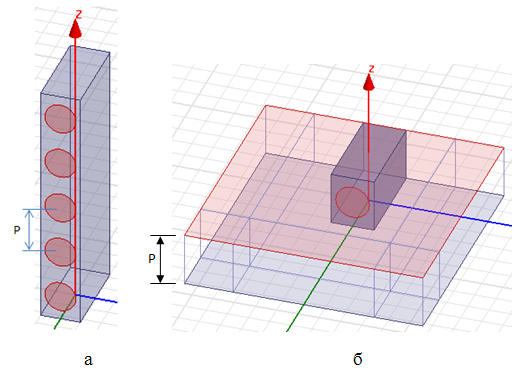
Рис. 1. а – Фрагмент прямоугольного волновода с линейной решеткой круглых отверстий в узкой стенке;
б – модель для расчета постоянной распространения

Ячейка волновода с длиной по оси Z, равной периоду р, заключена между горизонтальными плоскостями, на которых заданы граничные условия периодического типа. Ячейка расположена в воздушном боксе, на трех гранях которого формируются согласующие слои, определяемые как perfect matched layers (PML). Грани воздушного бокса и PML отстоят от выделенных граней ячейки волновода на расстояние не менее четверти длины волны в свободном пространстве. Предполагается, что эти слои полностью поглощают падающее на них излучение из волновода. Четвертая грань бокса представляет металлическую плоскость, которая примыкает к задней узкой стенке волновода. При этом волновод излучает через отверстия, расположенные на передней узкой стенке.

Метод решения состоит в следующем. По заданному фазовому набегу на периоде структуры программа находит собственную частоту эквивалентного резонатора на рис. 1б. Действительная часть частоты Re(f) определяет нормированную фазовую постоянную распространения волны:

, (1)

где - фазовый набег на периоде p, k=2π/λ, λ =c/Re(f) – длина волны в свободном пространстве, c- скорость света. Мнимая часть частоты Im(f) определяет мнимую часть постоянной распространения [14]:

(2)

Величина v_g - групповая скорость волны, которая в общем случае вычисляется через производную фазовой скорости по частоте:

(3)

Если фазовая скорость в возмущенном волноводе незначительно отличается от фазовой скорости в невозмущенном закрытом волноводе и не испытывает резких изменений от частоты, то можем предполагать, что групповая скорость в возмущенном волноводе связана с фазовой так же, как и в закрытом волноводе, то есть в этом случае приближенно выполняется соотношение v_gv_p ≈ c², c - скорость света в материале, заполняющем волновод. Можно показать, что при этом справедлива упрощенная формула для нормированной постоянной вытекания, не требующая вычисления производной по частоте:

(4)

В этой формуле добротность эквивалентного резонатора определяется как Q=Re(f)/(2*Im(f)). Следует отметить, что в окрестности резонанса в периодической структуре постоянная распространения испытывает резкое изменение в узкой полосе частот, и в этом случае групповую скорость необходимо вычислять через производную по частоте от фазовой скорости в соответствии с общей формулой (3). Таким образом, метод расчета комплексной постоянной распространения вытекающей моды состоит в следующем. Задавая разные значения фазового сдвига на периоде, находим соответствующие комплексные собственные частоты эквивалентного резонатора Re(f) и Im(f) и по ним рассчитываем значения нормированной фазовой постоянной и постоянной вытекания по вышеприведенным формулам.

На рис. 2а,б представлены рассчитанные этим способом частотные зависимости нормированной фазовой постоянной распространения и постоянной вытекания для основной ТЕ₁₀моды. На тех же рисунках для сравнения показаны соответствующие зависимости, рассчитанные по аналитическим формулам. Видим, что имеет место совпадение с графической точностью для фазовой постоянной распространения, рассчитанной численным методом и аналитически.

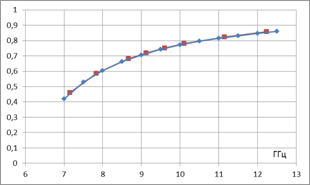
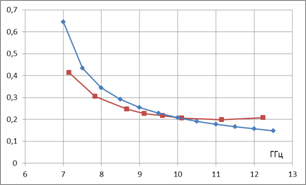
а б

Рис. 2. Распространение вытекающей ТЕ₁₀ моды в прямоугольном волноводе с линейной решеткой из круглых отверстий в узкой стенке:
а – нормированная фазовая постоянная распространения β/k;
б – постоянная вытекания α, неп/м.
Кривые красного цвета – численный расчет, синего цвета – расчет по приближенным аналитическим формулам

Определенное расхождение численных и аналитических результатов для постоянной вытекания может быть обусловлено некоторым отличием численной модели на рис. 1б от аналитической модели и принятыми в последней допущениями.

На рис.3 показаны примеры распределения амплитуды напряженности электрического и магнитного полей вытекающей ТЕ₁₀ моды внутри ячейки на частоте 10.10 ГГц, при которой сдвиг фазы на периоде равен 120°. Наглядно отображается явление вытекания электромагнитной энергии через круглое отверстие, которое формирует излучение в антенне вытекающей волны.

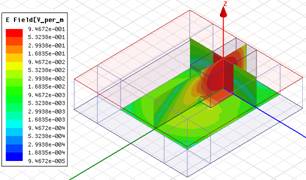
а б

Рис. 3. Распределение амплитуды напряженности электрического поля (а)
и магнитного поля (б) вытекающей ТЕ₁₀моды в ячейке в различных сечениях. Частота 10.10 ГГц

Двумерная решетка в плоском волноводе

Метод может быть применен также к расчету постоянной распространения вытекающих волн в планарных двумерно-периодических структурах. В качестве примера рассмотрим плоский волновод с двумерной решеткой из круглых отверстий в экране, фрагмент которого показан на рис. 4а. Можно представить эту структуру как композицию из прямоугольных волноводов на рис. 1а, примыкающих друг к другу широкими стенками. Для распространяющейся вдоль оси Z волны с вектором Е, направленным перпендикулярно к широким стенкам (ТЕ-волны), эти стенки можно убрать без влияния на постоянную распространения. На рис. 4б представлена модель ячейки, которая ограничена сверху и снизу плоскостями, на которых заданы граничные условия периодического типа по аналогии с рассмотренной выше моделью. На плоскостях, ограничивающих ячейку слева и справа, также задаются граничные условия периодического типа для волны, которая в общем случае может распространяться в произвольном направлении относительно оси Z. Если волна распространяется вдоль Z, эти граничные условия периодического типа можно заменить идеальными электрическими стенками для ТЕ волны или идеальными магнитными стенками для ТМ волны. Толщина плоского волновода определяется размером широкой стенки волновода на рис. 1а. В данной модели период вдоль Z равен 12.7 мм, в перпендикулярном направлении вдоль Y период равен 10.16 мм, который определяется размером узкой стенки волновода на рис. 1а. Как и выше, металлический экран с отверстиями предполагается бесконечно тонким и идеально проводящим.

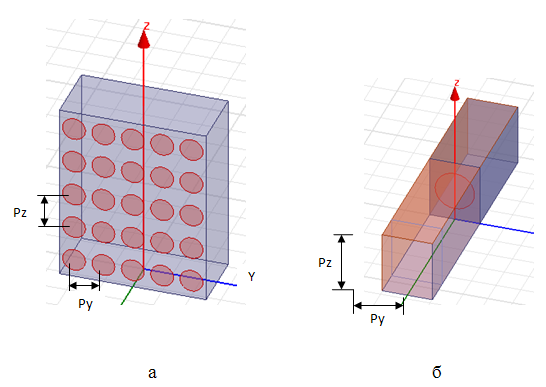
Рис. 4. а - Фрагмент плоского волновода с двумерно-периодической решеткой из круглых отверстий в экране;
б – модель ячейки структуры между двумя парами плоскостей с периодическими граничными условиями и с PML слоем

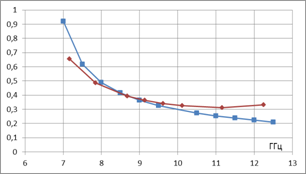
На рис. 5а,б представлены рассчитанные частотные зависимости нормированной фазовой постоянной распространения и постоянной вытекания ТЕ волны, бегущей вдоль Z. На тех же рисунках для сравнения показаны соответствующие величины, полученные по приближенным аналитическим формулам [7]. В этом случае также имеет место практически полное совпадение значений для фазовой постоянной распространения и некоторое расхождение для постоянной вытекания. Последнее может быть обусловлено теми же факторами, что и для рассмотренной выше линейной решетки, то есть определенным отличием численной модели на рис. 4б от аналитической модели в [7] и принятыми в той модели допущениями. Сравнивая постоянную вытекания в линейной (рис. 2б) и в двумерной (рис. 5б) решетках, видим, что в одном и том же диапазоне частот постоянная вытекания в плоском волноводе примерно в 1.5 раза больше, чем в прямоугольном. В этом проявляется взаимодействие по внешнему пространству излучателей в двумерной решетке.

а б

Рис. 5. Распространение вытекающей ТЕ волны в двумерной решетке из круглых отверстий в плоском экране: а – нормированная фазовая постоянная распространения β/k; б – постоянная вытекания α, неп/м. Кривые красного цвета – численный расчет, синего цвета – расчет по приближенным аналитическим формулам

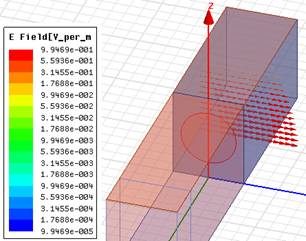
На рис. 6 представлен пример распределения вектора Е в двух ортогональных плоскостях внутри ячейки на частоте 8.68 ГГц (сдвиг фазы на периоде вдоль Z равен 90°). Эти распределения наглядно иллюстрируют и подтверждают ожидаемое распределение поля ТЕ волны в плоской решетке, бегущей в направлении оси Z. Волна имеет сходное распределение с основной ТЕ₁₀модой прямоугольного металлического волновода.

а б

Рис. 6. Распределение вектора Е в разных плоскостях внутри ячейки при распространении ТЕволны вдоль оси Z на частоте 8.68 ГГц: а – в плоскости ZY, б - в плоскости XY

Распространение под углом к оси Z

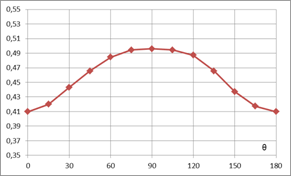
Как уже отмечалось, в структуре на рис. 4а волна может распространяться под любым углом относительно оси Z в зависимости от способа возбуждения. При этом нормированная фазовая постоянная и постоянная вытекания зависят от угла распространения. На рис. 7а,б представлены рассчитанные зависимости этих величин от угла θ, отсчитываемого от положительного направления оси Z, при фиксированном значении β =116.6 рад/м. Очевидно, обе зависимости должны быть симметричны относительно угла θ=90°. Небольшие отклонения от этой симметрии на рис. 7 связаны с погрешностью численного расчета собственных значений на модели рис. 4б, в которой используются две пары периодических граничных условий. Максимальное относительное изменение нормированной фазовой постоянной распространения при изменении угла составляет примерно 0.2%, а постоянной вытекания – около 20%. Таким образом, величина постоянной вытекания оказывается более зависимой от угла распространения. На рис. 8 а,б показаны распределения вектора Е для случая распространения волны под углом θ=45° на частоте 8.445 ГГц, при этом фазовые набеги на длине периодов вдоль Z и Y равны соответственно 60° и 48°. Наглядно проявляется наклон фазового фронта в плоскости ZY.

а б

Рис. 7. Рассчитанные зависимости от угла распространения ТЕволны относительно положительного направления оси Z:
а - нормированная фазовая постоянная распространения β/k; б - постоянная вытекания α, неп/м

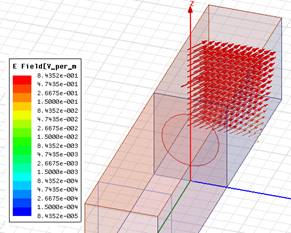
а б

Рис. 8. Распределение вектора Е внутри ячейки при распространении ТЕволны под углом 45° к оси Z на частоте 8.445 ГГц:
а – в плоскости ZY, б - в плоскости XY

Заключение

Предложенный в работе метод позволяет эффективно вычислять комплексную постоянную распространения вытекающих волн в волноводах со щелями. Обладая достаточно высоким быстродействием, он может служить для получения зависимостей фазовой постоянной и постоянной вытекания от параметров структуры. Сравнение с приближенным аналитическим методом показывает, что данный метод дает возможность получать более точные значения этих величин в некоторых частотных областях в пределах рабочей полосы волновода. Хотя в данной работе рассмотрены модели с бесконечно тонкими и идеально проводящими стенками, случай конечной толщины и конечной проводимости может быть рассмотрен аналогично и лишь с незначительной коррекцией численной модели. Кроме того, метод может быть применен не только для волноводов со щелями, но и для решеток других типов, например, образованных металлическими полосками, напечатанными на диэлектрике. Основная область применения метода - моделирование и проектирование антенн вытекающей волны.

Авторы выражают благодарность В. А. Калошину за обсуждение результатов и полезные замечания.

Литература

1. Y. J. Cheng, W. Hong, and K. Wu. Millimeter-Wave Substrate Integrated Waveguide Multibeam Antenna Based on the Parabolic Reflector Principle. IEEE Trans. on Antennas and Propagation, vol. 56, No. 9, Sept 2008, p. 3055-3058.

2. M. Ettorre, A. Neto, G. Gerini, and S. Maci. Leaky-Wave Slot Array Antenna Fed by a Dual Reflector System, IEEE Trans. on Antennas and Propagation, vol. 56, No. 10, Oct 2008, p. 3143-3149.

3. M. Ettorre, R. Sauleau, and L. Le Coq. Multi-Beam Multi-Layer Leaky-Wave SIW Pillbox Antenna for Millimeter-Wave Applications. IEEE Trans. on Antennas and Propagation, vol. 59, No. 4, Apr 2011, p. 1093-1100.

4. E. Schreiber, M. Peichl, M. Jirousek, H. Suess. VESAS: a novel concept for fully-electronic passive MW imaging. Proceedings of SPIE Defense, Security, and Sensing 2013, 8715 (87150J). SPIE Digital Library. SPIE Defense, Security, and Sensing 2013, Apr 29 –May3 2013, Baltimore, USA.

5. L. O. Goldstone and A. A. Oliner. Leaky-Wave Antennas I: Rectangular Waveguides. IRE Trans. on Antennas and Propagation, vol. AP-7, No. 4, 1959, p. 307-319.

6. M. Guglielmi and D. R. Jackson. Broadside Radiation from Periodic Leaky-Wave Antennas. IEEE Trans. on Antennas and Propagation, vol. 41, No. 1, Jan 1993, p. 31-37.

7. К. Уолтер. Антенны бегущей волны. Пер. с англ. под ред. А. Ф. Чаплина. М.: Энергия, 1970.

8. Антенны и устройства СВЧ. Проектирование фазированных антенных решеток: Учебное пособие для вузов. / В. С. Филиппов, Л. И. Пономарев, А. Ю. Гринев и др.; под ред. Д. И. Воскресенского. – 2-е изд., доп. и перераб. М.: Радио и связь, 1994.

9. Сазонов Д. М. Антенны и устройства СВЧ. М.: Высш. школа, 1988.

10. Бодров В. В., Сурков В. И. Математическое моделирование устройств СВЧ и антенн. М.: Изд-во МЭИ, 1994.

11. Панченко Б. А., Нефедов Е. И. Микрополосковые антенны. М.: Радио и связь, 1986.

12. F. Xu and K. Wu. Understanding Leaky-Wave Structures. IEEE Microwave Magazine, vol.14, No. 5, July/Aug.2013, p. 87-96.

13. Банков С. Е. Антенные решетки с последовательным питанием. М.: Физматлит, 2013.

14. F. Xu, A. Patrovsky, K. Wu. Fast Simulation of Periodic Guided-Wave Structures Based on Commercial Software. Microwave Opt. Technol. Lett., vol. 49, No.9, Sept. 2007, p. 2180-2182.

15. С. Е. Банков, Э. М. Гутцайт, А. А. Курушин. Решение оптических и СВЧ задач с помощью HFSS. М.: Оркада, 2012.