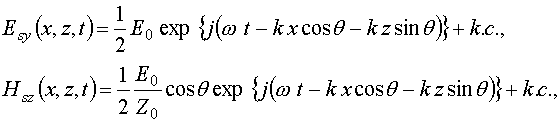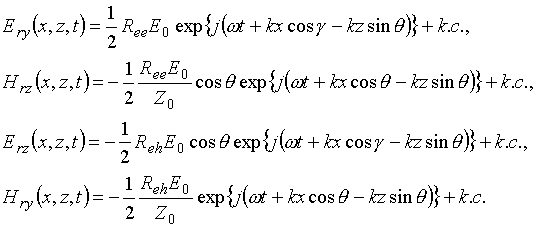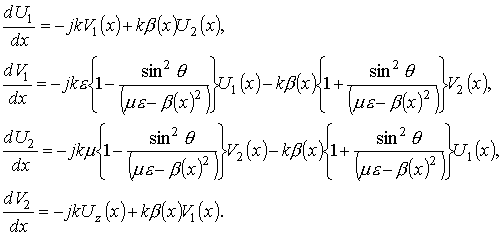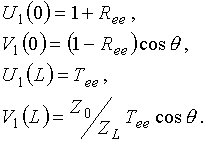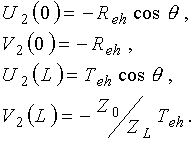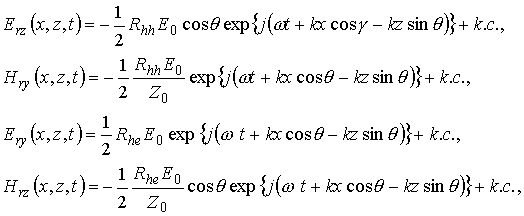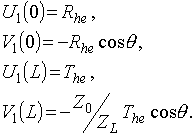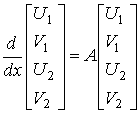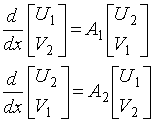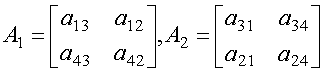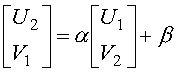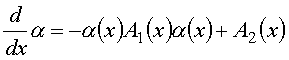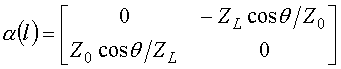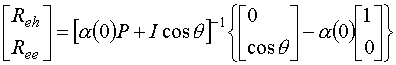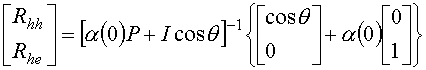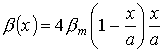Расчет отражения плоской поляризованной электромагнитной волны от неоднородного кирального слоя.

"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 5, 2001

РАСЧЕТ ОТРАЖЕНИЯ ПЛОСКОЙ ПОЛЯРИЗОВАННОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ ОТ НЕОДНОРОДНОГО КИРАЛЬНОГО СЛОЯ

Д. Н. Панин, В. В. Зайцев, Г. П. Яровой
Самарский государственный университет

Получена 22 марта 2001 г.

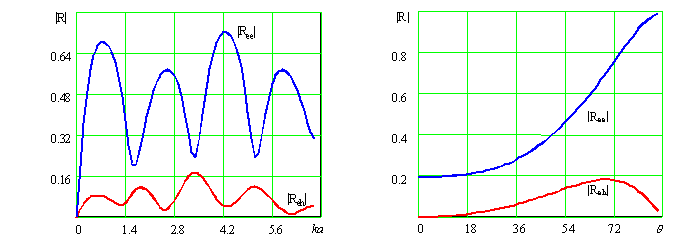
Предложена методика численного моделирования взаимодействия электромагнитного излучения с плоским киральнным слоем с произвольными пространственными профилями электрофизических параметров. Приведены результаты анализа частотных и угловых характеристик коэффициента отражения волн Е - и Н - поляризации.

1. Введение

Электродинамика киральных сред вызывает в последние годы устойчивый и все возрастающий интерес [1, 2]. Применение искусственных киральных материалов в волноводных элементах техники СВЧ, при создании поглощающих покрытий и полупрозрачных экранов представляется весьма перспективным и с ними связаны надежды, как на улучшение характеристик традиционных устройств, так и на появление новых технических решений.

Будучи изготовленными из материалов со сложной макроскопической структурой, киральные электродинамические системы являются, как правило, неоднородными. В ряде случаев неоднородность вводится целенаправленно для достижения заданных свойств системы. Так как точные аналитические решения для волн в неоднородных средах удается получить лишь для самых простых моделей неоднородностей [3], то при исследовании реальных структур на первый план выходят численные методы.

В настоящей работе предложенный ранее [4] метод расчета отражений электромагнитной волны от слоя неоднородной плазмы распространен на слой киральной среды с произвольным пространственным профилем параметра киральности. Проведен анализ частотных и угловых зависимостей коэффициентов отражений волн Е- и Н–поляризаций.

2. Наклонное падение электромагнитной волны Е – поляризации на киральный слой

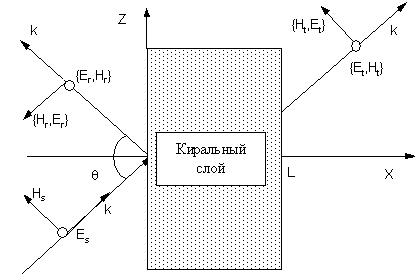
Рассмотрим электродинамическую систему, представляющую собой киральный слой, расположенный между плоскостями x=0 и x=L декартовой системы координат (рис.1). В дальнейшем пространство x<0, будем обозначать как область 1, а пространство x>L - как область 2. В области 1 на границу слоя под углом q падает плоская с E–поляризованная волна, т.е. волна с вектором напряженности магнитного поля, лежащим в плоскости слоя: , . При этом составляющие полей и можно представить в виде:

(1)

где w и k– частота и волновое число, E₀ – комплексная амплитуда напряженности электрического поля, Z₀– импеданс однородной области 1.

Рис. 1

Кроме падающей волны в области 1 в общем случае существует также основная отраженная волна, имеющая y-компоненту напряженности электрического поля, x и -– компоненты напряженности магнитного поля, и деполяризованная отраженная волна, имеющая y-компоненту напряженности магнитного поля, x и z- компоненты напряженности электрического поля:

(2)

где –коэффициенты отражения основной и деполяризованой волн в случае Е-поляризации.

В области 2 существует прошедшая волна, соответствующие компоненты которой можно записать как

(3)

где коэффициенты прохождения основной и деполяризованной волн в случае Е-поляризации, - волновое сопротивление во второй области.

В неоднородном киральном слое, описанным материальными уравнениями вида

пространственные зависимости z-составляющей напряженности магнитного поля и y–составляющей напряженности электрического поля основной волны, y-составляющей напряженности магнитного поля и z–составляющей напряженности электрического поля описываются уравнениями Максвелла, которые для гармонических полей имеют вид:

(4)

Здесь - параметр киральности.

Если ввести в рассмотрение нормированные напряженности электрического и магнитного полей, то уравнения (4) можно записать следующим образом:

(5)

Для системы уравнений (5), исходя из условий непрерывности тангенциальных составляющих напряженностей электрического и магнитного полей на границах раздела сред, с учетом (1)-(3) имеем следующие граничные условия:

(6)

3. Электромагнитная волна Н - поляризации

Падающая на слой под углом q к его нормали электромагнитная волна Н-поляризации имеет только одну составляющую вектора напряженности магнитного поля и две составляющих вектора напряженности электрического поля . Лежащие в плоскости слоя проекции векторов описываются выражениями:

(7)

Соответствующие проекции в отраженной волне записываются в виде

(8)

где –коэффициенты отражения основной и деполяризованой волн в случае Н-поляризации.

А для прошедшей через слой волны в области 2 имеем:

(9)

где коэффициенты прохождения основной и деполяризованной волн в случае Н-поляризации.

Вид уравнений, описывающих волновые поля в киральной среде, такой же, как и в случае Е-поляризации, а граничные условия с учетом выражений (7)-(9) представляются в следующем виде:

(10)

4. Метод дифференциальной прогонки для расчета частотных зависимостей коэффициента отражения волны Е- и Н-поляризации.

Системы уравнений (5) вместе с условиями (6) и (10) составляют граничные задачи, решение которых позволяет определять волновые поля в киральном слое. При изменении волнового числа k можно рассчитать частотные зависимости коэффициентов отражения слоя. Однако (5) являются уравнениями с переменными коэффициентами, и их аналитическое решение возможно только для небольшого числа модельных зависимостей .

Методом дифференциальной прогонки граничные задачи данного типа можно свести в задачи Коши.

Запишем уравнения Максвелла в матричной форме:

, где (11)

Преобразуем (11) к виду:

, (12)

где .

Решение для системы (12) будем искать в виде

(13)

для случая Е-поляризации и Н-поляризации.

Продифференцировав (13) получаем матричное уравнение следующего вида:

(14)

с начальным условием

(15)

Тогда из граничных условий (6) и (10) следует

, (16)

для случая Е-поляризации и

(17)

для случая Н-поляризации.

Здесь , .

Таким образом, решая задачю Коши (14-15), из (16) и (17) мы можем найти частотные и угловые зависимости коэффициентов отражения.

5. Основные результаты и выводы.

В качестве примера приведем результаты расчетов для слоя с ограниченным параболическим профилем параметра киральности:

где – максимальное значение параметра киральности, а – толщина кирального слоя. На рис.2 и рис.3 приведены графики частотных и угловых зависимостей модулей коэффициентов отражения основной () и деполяризованной () волн. Падающая под углом плоская волна Е-поляризована, диэлектрическая проницаемость слоя постоянна , нормированная частота .

Результаты анализа частотных и угловых зависимостей коэффициентов отражения полезны при разработке методик измерения параметра киральности искусственных композитных материалов.


Рис. 2	Рис. 3

Литература

1. Каценеленбаум Б.З., Коршунова Е.Н., Сивов А.Н., Шатров А.Д. Киральные электродинамические объекты // Успехи физических наук. – 1997. – Т. 167, № 11. – С. 1201.

2. Третьяков С.А. Приближенные граничные условия для тонкого биизотропного слоя // Радиотехника и электроника. – 1994. –Т. 39, № 2. – С. 184.

3. Неганов В.А., Раевский С.Б., Яровой Г.П. Линейная макроскопическая электродинамика. – М.: Радио и связь, 2000.

4. Зайцев В.В., Панин Д.Н., Яровой Г.П. Численное моделирование отражений электромагнитной волны от неоднородного кирального слоя // VIII международная научно-техн. конф. "Оптические, радиоволновые и тепловые методы и средства контроля качества материалов, промышленных изделий и окружающей среды". Тез. докл. – Ульяновск, 2000. – С. 157.

Авторы:

Панин Дмитрий Николаевич (аспирант), e-mail: persey22@mail.ru, Зайцев Валерий Васильевич (канд. физ.-мат. наук, доцент), Яровой Геннадий Петрович (доктор физ.-мат. наук, профессор)

Самарский государственный университет, кафедра радиофизики и компьютерного моделирования радиосистем.

оглавление

дискуссия