 |
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 6, 2004 |
 |
Расчет диаграммы направленности внеосевых зеркальных
многолучевых антенн миллиметрового диапазона
Федеральное Государственное Унитарное Предприятие Специальное Конструкторское Бюро Института Радиотехники и Электроники Российской Академии Наук (ФГУП СКБ ИРЭ РАН)
Получена 07.06.2004 г.
Предложен новый метод расчета диаграммы направленности внеосевых зеркальных многолучевых антенн миллиметрового диапазона, который заключается в замене части подынтегральной функции интерполяционным бикубическим сплайном. Показана высокая эффективность и универсальность метода, которая подтверждена практическими измерениями.
Содержание
1. Введение
Внеосевые зеркальные антенны СВЧ обладают рядом преимуществ по сравнению с осевыми антеннами (отсутствие затенения апертуры рупором и вспомогательными конструкциями, минимизация переотражений в системе “рупор-зеркало” и т.д.). Однако анализ таких антенн затруднителен из-за отсутствия круговой симметрии системы. Для многолучевых антенн задача расчета диаграммы направленности (далее ДН) еще более усложняется, т.к. нефокальное положение облучателя не позволяет пользоваться многими приближениями, применимыми для случая, когда облучатель находится в фокусе. Здесь и далее под положением облучателя понимается положение его условного фазового центра, который определяется в работах [1, p. 712-714] и [6]. Целью настоящей работы является описание нового метода расчета ДН многолучевых внеосевых зеркальных антенн миллиметрового диапазона.
2. Описание проблемы
Геометрия внеосевой зеркальной антенны со смещенным из фокуса F облучателем представлена на рис. 1,
Рис. 1. Внеосевая зеркальная антенна со смещенным облучателем.
где
S – поверхность зеркала;
F – фокус параболоида вращения и начало координат;
M – положение облучателя;
P – точка наблюдения.
Отражатель (далее зеркало) внеосевой зеркальной антенны представляет собой сечение параболоида вращения с осью вращения Z внеосевым цилиндром. Нормированная ДН зеркальной антенны может быть представлена как [1, p. 124, 808]:
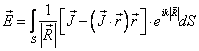
(1 а)
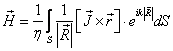
(1 б)
где
– поверхностная
плотность тока;
– нормаль к поверхности
зеркала;
– магнитная компонента волны,
падающей на зеркало;
–
вектор с началом в точке на поверхности S и с концом в точке наблюдения P;
;
–
волновое сопротивление вакуума;
–
волновое число, λ – длина волны.
Если в качестве облучателя в антенне используется электромагнитный рупор, то:
(2)
где
–
апертура рупора;
– электрическая компонента поля в
апертуре рупора;
– вектор
с началом в точке на апертуре рупора и с концом в точке на
поверхности S;
.
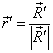Прямое
вычисление интегралов (1а, 1б) возможно только для зеркал, размеры которых не
превышают 10-15 длин волн, иначе затраты машинного времени становятся
неприемлемыми для большинства практических задач. Большие затраты машинного
времени связаны, в первую очередь, с тем, что поверхностная плотность тока 
в
общем случае выражается интегралом (2). Возможным способом
решения этой проблемы явилась бы замена интегрального представления на
более простое, которое уже не требует больших затрат времени на его вычисление,
однако, учитывая некоторую произвольность функции (строго
говоря, определенно можно утверждать только то, что она гладкая и непрерывная
на всей поверхности S),
ее нельзя заменить какой-либо простой комбинацией элементарных функций без
существенного сужения класса решаемых задач. Другим способом является
применение интерполяционных формул, например интерполяция полиномами
Лагранжа [2, стр. 20]. Однако для некоторых функций
интерполяционный полином Лагранжа не только не приближается к интерполируемой
функции, но и может отличаться от нее на любую, произвольно заданную, величину
[2, стр. 22]. К тому же, полиномиальная интерполяция
потребовала бы привлечения полиномов довольно высоких порядков (в силу произвольности
), что существенно уменьшило бы выигрыш от
ее использования. Другой подход к задаче интерполяции – кусочно-полиномиальная
интерполяция, называемая также сплайном [2, 3] – не содержит перечисленных недостатков, свойственных
методам полиномиальной интерполяции.
3. Метод расчета ДН
Свойства сплайнов и процедура их построения достаточно подробно описаны в работах [2, 3], однако, для дальнейшего применения сплайн-интерполяции к задаче расчета ДН, отметим следующие особенности сплайн-функций двух переменных 3-го порядка (называемых также бикубическими сплайнами), построенных на интерполяционной сетке размера m×n:
1) сплайн-функция проходит через все точки заданного массива;
2) заданным массивом сплайн-функция определяется однозначно;
3) степень полиномов не зависит от числа узлов сетки;
4) бикубический сплайн имеет непрерывные производные вплоть до второго порядка включительно;
5) последовательность интерполяционных бикубических сплайнов на равномерной сетке всегда сходится к интерполируемой непрерывной функции с увеличением числа узлов сетки;
6) точность интерполяции зависит от гладкости интерполируемой функции: чем функция более гладкая – тем меньше ошибка интерполяции;
Процедура
построения интерполяционного бикубического сплайна [2,
стр. 56-74] может быть применена к задаче интерполяции каждой из трех
декартовых компонент (которые в общем случае являются
комплексными) при условии, что коэффициенты полиномов, образующих сплайн, также
будут комплексными. Это эквивалентно раздельной интерполяции реальной и мнимой
части каждой декартовой компоненты . Возможна также
раздельная интерполяция амплитуды и фазы , однако, этот способ
более сложен алгоритмически и не приводит к увеличению точности интерполяции.
Для непосредственной
интерполяции необходимо большое количество узлов
интерполяционной сетки. Это связано с быстрым изменением фазы на
поверхности зеркала (в особенности это справедливо для короткофокусных антенн).
Апертурное приближение интегралов (1а, 1б), которое могло бы помочь в решении
этой проблемы, не подходит для задачи точного расчета ДН, т.к. оно имеет смысл
только в предположении, что источник падающей на зеркало электромагнитной волны
имеет фазовый центр. Но волновой фронт рупорного облучателя не является, вообще
говоря, сферическим (следовательно, фаза также не является
сферической) [1, p.712-714], и не может быть описан аналитически, однако всегда
можно выделить сферическую составляющую поверхностной плотности тока .
Представим как:
(3)
где
– вектор
с началом в условном фазовом центре облучателя M и с концом в
точке на поверхности S
(см. рис. 1);
–
медленно меняющаяся по фазе компонента .
Подставляя (3) в (1а, 1б) получим следующие выражения для ДН:
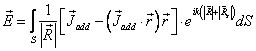
(4 а)
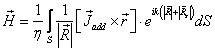
(4 б)
Вообще говоря, совпадение
фазового центра выделенной сферической компоненты с
условным фазовым центром рупора не требуется, но в случае их совпадения
изменение по фазе на S минимально.
Положение условного фазового центра облучателя может быть определено численно,
но для практических расчетов достаточно поместить фазовый центр сферической
компоненты в любой точке, находящейся на
расстоянии нескольких длин волн от условного фазового центра облучателя,
например, в центре апертуры рупора.
Интерполяция уже не требует столь частой
интерполяционной сетки, как и выигрыш в скорости
вычислений становится существенным.
При проектировании многолучевых зеркальных антенн возникает задача определения пространственного положения главного лепестка ДН в случае облучателя, вынесенного из фокуса. Оптимальное положение вынесенных облучателей в многолучевой антенне можно приближенно определить как плоскость, проходящую через фокус параболического зеркала и являющуюся касательной к сфере с центром в точке пересечения оси внеосевого секущего цилиндра с поверхностью параболоида вращения (см. выше) и проходящую через фокус параболоида [4]. Для поиска пространственного положения луча можно воспользоваться любым подходящим методом оптимизации (например, методом Пауэлла или градиентным методом [5]). В качестве начальной точки поиска луча удобно взять его положение в приближении геометрической оптики, которое может быть легко вычислено аналитически.
Отметим, что форма поверхности зеркала S анализируемой антенны может быть непараболической. В предлагаемом методе расчета ДН достаточно, чтобы поверхность S описывалась гладкой функцией, и ее радиус кривизны в каждой точке был много больше длины волны. Следовательно, метод позволяет анализировать влияние технологических деформаций зеркала на ДН и рассчитывать ДН двухзеркальных внеосевых антенн.
Алгоритм расчета ДН внеосевой зеркальной антенны со смещенным облучателем выглядит следующим образом:
1) вычисляется
поле в апертуре рупора (используя
аналитические приближения для применяющегося типа рупора, либо численно решая
уравнения Максвелла методом конечных элементов или методом FDTD – Finite Difference of Time Domain);
2) вычисляется
в узлах интерполяционной сетки на
зеркале путем интегрирования поля в апертуре рупора по формуле (2);
3) выделяется
медленно меняющаяся по фазе компонента поверхностной плотности тока 
по
формуле (3);
4) определяется пространственное положение главного лепестка ДН подходящим методом оптимизации (напр. методом Пауэлла);
5) заменяется
интерполяционным бикубическим сплайном и ДН вычисляется по формулам (4а, 4б)
подходящим методом численного интегрирования (напр. методом Гаусса).
4. Применение предложенного метода расчета ДН к анализу 64-лучевой внеосевой зеркальной антенны 3мм диапазона
Предлагаемый метод использовался для расчета ДН 64-лучевой внеосевой зеркальной антенны 3мм диапазона, со следующими параметрами:
·
фокусное
расстояние –
·
диаметр
зеркала
–
·
возвышение
–
·
длина
рупора
–
· апертура рупора – 14.6×11.2 мм;
· волновод – WR-10 (2.54×1.27 мм);
· диапазон рабочих частот – 92-96 ГГц;
· рабочая поляризация – вертикальная;
· режим работы – прием.
Облучатели в антенне представляли собой матрицу 8×8 пирамидальных рупоров.
При вычислении диаграммы направленности отдельного рупора, поле в его апертуре представлялось в приближении [1, p. 682], т.е. с косинусоидальным распределением амплитуды и параболическим – фазы. Это приближение достаточно хорошо описывает поле в апертуре узкоугольного пирамидального рупора. Интегрирование поля в апертуре рупора по формуле (2) проводилось методом Гаусса 16-го порядка по адаптивной схеме с относительной погрешностью 10-6.
Нормированные модули декартовых компонент поверхностной плотности тока на зеркале для крайнего верхнего рупора матрицы представлены на рис. 2-7. Крайний верхний рупор выбран как случай, наиболее сложный для анализа. На этих рисунках модули токов показаны в декартовой системе координат апертуры зеркала, начало координат совпадает с фокусом зеркала F (см. рис. 1). Нормировка токов проводилась на максимум модуля полного вектора тока:
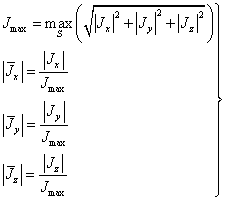
(5)
Поверхностная плотность тока вычислялась
в узлах цилиндрической интерполяционной сетки размера 30×90 (30 узлов по
радиусу, 90 – по углу). Для выделения сферической компоненты ее
фазовый центр помещался в центре апертуры рупора. Далее заменялась
интерполяционным бикубическим сплайном для каждой комплексной декартовой
компоненты . Вычисление интегралов (4а, 4б)
проводилось методом Гаусса 16-го порядка по адаптивной схеме с относительной
погрешностью 10-5. Поиск пространственного положения луча проводился
методом Пауэлла [5] с погрешностью 0.001 мрад. Расчет 100 точек ДН на
компьютере Pentium-IV 3 ГГц занимает
около 5 сек.
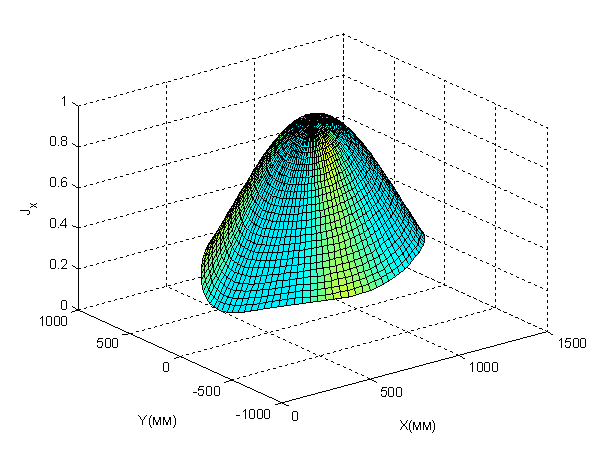
Рис. 2. Нормированный модуль X-компоненты
поверхностной плотности тока на поверхности
параболического зеркала 64-лучевой антенны, обусловленного облучением крайнего
верхнего рупора (
). 3-мерный вид.
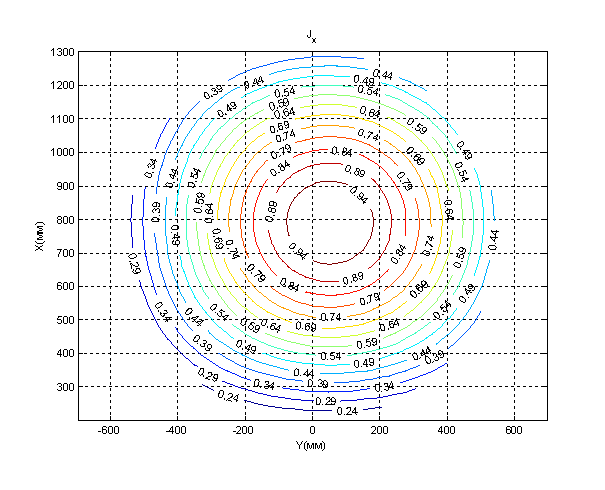
Рис. 3. Нормированный модуль X-компоненты
поверхностной плотности тока на поверхности
параболического зеркала 64-лучевой антенны, обусловленного облучением крайнего
верхнего рупора (). Линии уровня.
Рис. 4. Нормированный модуль Y-компоненты
поверхностной плотности тока на поверхности
параболического зеркала 64-лучевой антенны, обусловленного облучением крайнего
верхнего рупора (). 3-мерный вид.
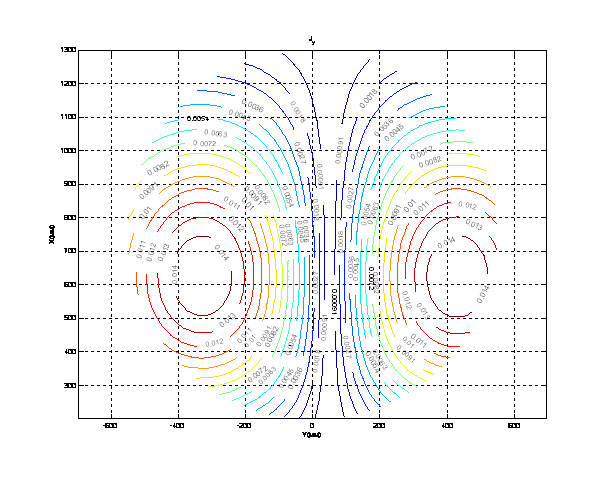
Рис. 5. Нормированный модуль Y-компоненты
поверхностной плотности тока на поверхности
параболического зеркала 64-лучевой антенны, обусловленного облучением крайнего
верхнего рупора (). Линии уровня.
Рис. 6. Нормированный модуль Z-компоненты поверхностной плотности тока на
поверхности параболического зеркала 64-лучевой антенны, обусловленного
облучением крайнего верхнего рупора (). 3-мерный вид.
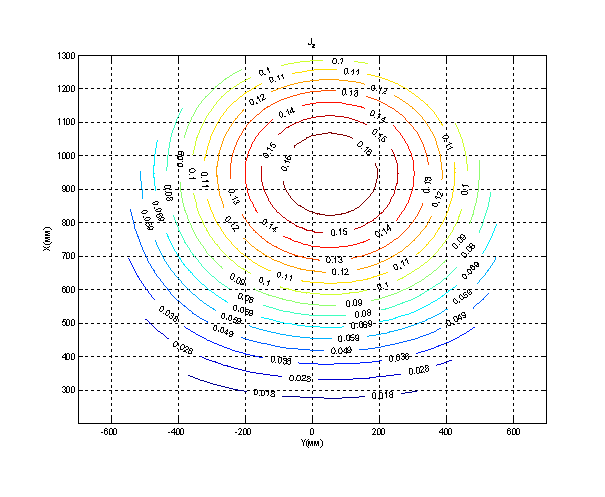
Рис. 7. Нормированный модуль Z-компоненты
поверхностной плотности тока на поверхности
параболического зеркала 64-лучевой антенны, обусловленного облучением крайнего
верхнего рупора (). Линии уровня.
Расчетные и экспериментальные ДН для одной из центральных “строк” матрицы
рупоров для представлены
на рис. 8 (под ДН многолучевой антенны будем понимать совокупность всех
отдельных ДН для каждого канала). На рис. 9-10 представлены расчетные и
экспериментальные ДН в вертикальной и горизонтальной плоскостях
для одного луча, соответствующего крайнему верхнему рупору матрицы. Погрешность
измерения ДН на рис.8-10 составляет ±0.6 дБ и, в основном, определяется
параметрами радиометра (ошибка калибровки входного аттенюатора, неидеальность
термостатирования, нелинейность квадратичного детектора и т.д.). Учет
технологических деформаций зеркала для представленных
ДН не проводился.
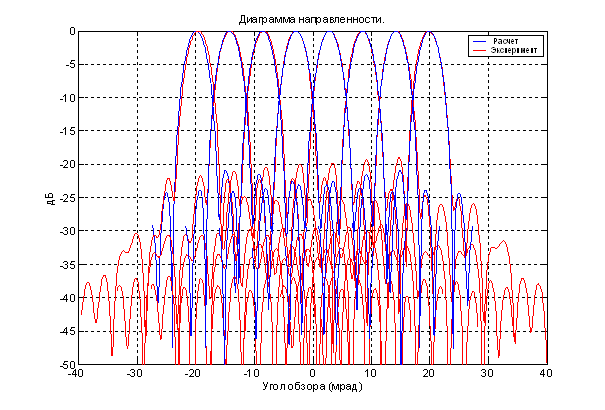
Рис. 8. Расчетные и экспериментальные ДН однозеркальной
внеосевой 64-лучевой антенны в горизонтальной плоскости ().
Взаимное положение лучей.
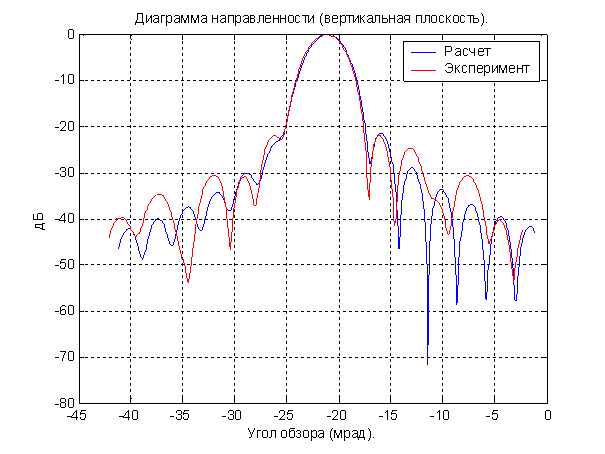
Рис. 9. Расчетная и экспериментальная ДН
однозеркальной внеосевой 64-лучевой антенны в вертикальной плоскости ().
Один луч.
Рис. 10. Расчетная и экспериментальная ДН
однозеркальной внеосевой 64-лучевой антенны в горизонтальной плоскости ().
Один луч.
На рис. 11 представлены расчетные ДН для всех 64-х рупоров в 3-мерном виде в системе координат “азимут (горизонтальный угол) – угол места (вертикальный угол)”.
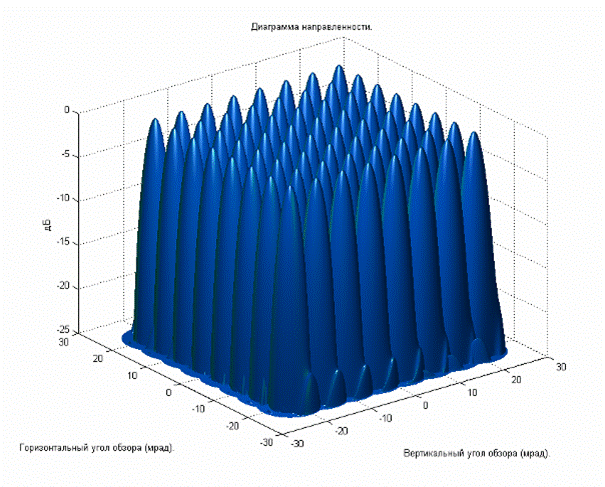
Рис. 11. Расчетные ДН однозеркальной внеосевой 64-лучевой
антенны (). 64 луча, 3-мерный вид.
Т.о. предложенный метод расчета ДН дает достаточно точные результаты при высокой скорости вычислений. Являясь универсальным и независимым от конфигурации антенны в широких пределах, он позволяет быстро и точно вычислять ДН внеосевых многолучевых зеркальных антенн миллиметрового диапазона и позволяет учитывать влияние технологических деформаций зеркала на ДН. Предложенный метод может применяться также для расчета ДН двухзеркальных антенн.
ЛИТЕРАТУРА
1. С. A. Balanis, Antenna theory:
analysis and design. Second edition. John Wiley & Sons Inc., 1997, 941 p.
2. Е.В. Шикин, А.И. Плис, Кривые и поверхности на экране компьютера. Руководство по сплайнам для пользователей, М.: ДИАЛОГ-МИФИ, 1996, 240 с.
3. С.Б. Стечкин,
Ю.Н. Субботин, Сплайны в вычислительной математике, М.: Наука. Главная редакция физико-математической литературы. 1976. 248 с.
4. R. Mittra, Y. Rahmat-Samh, V. Galindo-Israel, R. Norman, An Efficient Technique for the Computation of Vector Secondary Patterns of Offset Paraboloid Reflectors /IEEE Trans. Antennas Propagat. 1979/ V. AP-27. № 3 p.294-304
5. К. Гупта, Р.
Гардж, Р. Чадха, Машинное проектирование СВЧ устройств. М.: Радио и связь. 1987. 432 с.
6. J. D. Dyson, Determination of the
Phase Center and Phase Patterns of Antennas /Radio Antennas for Aircraft and
Aerospace Vehicles/, W.T. Blackband (ed.), AGARD Conference Proceedings,
No. 15, Slough, England Technivisison Services, 1967
 |
 |