УДК 621.391
ОБНАРУЖЕНИЕ ПОЧТИ-ПЕРИОДИЧЕСКИХ ПОТОКОВ
Ф. В. Голик
Новгородский государственный университет им. Ярослава Мудрого
Получена 12 июня 2010 г.
Аннотация. Предложена методика обнаружения периодичности потоков со случайным периодом следования точек. Получены оценки вероятностных характеристик обнаружения.
Ключевые слова: случайный поток, девиация частоты, пассивная радиолокация.
Содержание
Периодический поток с равномерной вобуляцией периода
Вероятности ошибок обнаружения
Периодический поток с нормальной вобуляцией периода
Вероятности ошибок обнаружения
Поток с накоплением дисперсии и нормальной вобуляцией
Простейший (пуассоновский) поток
Введение
Случайные потоки исследуются в теории массового обслуживания [1], [2], [3], [4] и др., теории надежности [5], радиолокации и связи [6…15]. При анализе потоков основное внимание уделяется оценке законов распределения интервалов между точками потока, распределению числа точек, а также исследованию спектральных и корреляционных характеристик.
В прикладных областях, таких как радиотехника, медицина, экономика, финансы и др., зачастую возникает задача обнаружения периодических потоков или выявление периодичностей в суперпозиции потоков. В радиотехнике это позволяет обнаружить детерминированную составляющую – сигнал, а в финансово-экономической области прогнозировать время появления очередного события.
На наш взгляд, вопросы обнаружения периодичностей в потоках не нашли достаточного освещения в литературе. Настоящая работа посвящена решению частной задачи – вопросам обнаружения периодичности потоков однородных событий с компенсируемой эпохой.
Постановка задачи
В общем случае механизм формирования потока
можно представить следующим образом. Пусть существует некоторый случайный
процесс. Зададим постоянный порог. Моменты времени, соответствующие пересечению
порога случайным процессом[1]
и образуют поток однородных событий или поток точек[2] 
. Здесь N – количество
точек или размер потока[3],
-
момент возникновения первой точки или эпоха потока.
Уточним понятие периодичности. Для
периодической функции 
выполняется условие 
, где T –
период. Под действием шумов и помех возникают искажения: 
и 
где 
- случайная величина. При
выполнении неравенства 
будем называть функцию 
-периодической. Очевидно,
что поток, порожденный процессом , так же является -периодическим.
Отметим, что к классу -периодических потоков
относятся потоки, порождаемые почти-периодическими функциями, которые «обладают
дискретным спектром из произвольно расположенных на шкале частот спектральных линий»
[17].
Целью настоящей работы является разработка процедуры обнаружения периодичности потоков и оценки характеристик обнаружения. Рассматриваются следующие потоки:
- поток с реперными точками, следующими с
неизвестным периодом T и случайной равномерной девиацией на интервале 
:
;
(- поток с реперными точками, следующими с неизвестным периодом T и случайной нормальной девиацией:
; (где 
- плотность нормального распределения с
параметрами 
.
- поток с нормальным независимым распределением интервалов между точками:
(- поток с экспоненциальным распределением интервалов между точками (простейший или пуассоновский):
(где 
- плотность распределения случайной
величины x, а 
- интенсивность потока.
На практике потоки вида (1) и (2) возникают при обнаружении моментов появления видео или радиоимпульсов при воздействии помехи, а также сигналов с времяимпульсной модуляцией. Поток вида (3) может порождаться сигналами с широтно-импульсной модуляцией. При этом, естественно, законы распределения интервалов зависят от свойств модулирующего сигнала и могут отличаться от принятых в рассматриваемых моделях.
Поток (4) может служить моделью моментов возникновения импульсов хаотической помехи.
Отметим, что дисперсия моментов появления точек потоков (1) и (2) постоянна и не зависит от номера точки. Потоки (3) и (4) не обладают этим свойством и относятся к классу потоков с накоплением дисперсии моментов возникновения точек[4].
Периодический поток с равномерной вобуляцией периода
Поставим в однозначное соответствие точкам
потока (1) дельта-функции 
и найдем косинус преобразование
потока дельта-функций [19]:
где 
– взаимно независимые
случайные величины, равномерно распределенные на интервале ; 
- эпоха.
Можно показать, что математическое ожидание и дисперсия функции (5) равны соответственно:
где
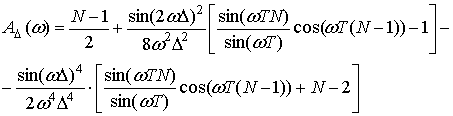
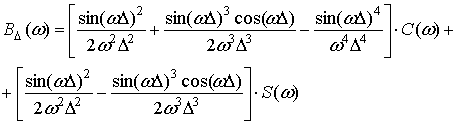
- относительная девиация периода.
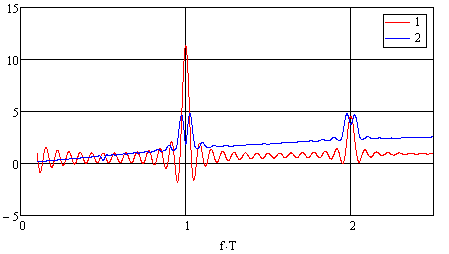
Рис. 1 Математическое ожидание и среднее квадратическое отклонение косинус-преобразования потока. N =15, δ=0.15. 1). Математическое ожидание. 2). С.к.о.
Максимумы среднего значения находятся в
точках fT=1, 2,…k,
что говорит о возможности оценки периода потока. С ростом k
величина максимумов уменьшается. Это снижает вероятность ошибочной оценки
периода, когда вместо истинного периода обнаруживается кратный. Расчеты
показывают, что при 
локальный максимум в точке fT=2 не превышает амплитуды колебаний на «промежуточных»
частотах.
Характерно, что дисперсия в среднем увеличивается с ростом fT. Это объясняется накоплением случайных фазовых сдвигов косинусоидальных составляющих (5).
Распределение косинус-преобразования 
хорошо
аппроксимируется гауссовым при всех 
, за исключением окрестностей точек 
. Это
позволяет найти границы доверительного интервала. На рис. 2 представлены
графики математического ожидания, границ доверительного интервала при доверительной
вероятности 0.997 и одной из случайных реализаций при N=15,
.
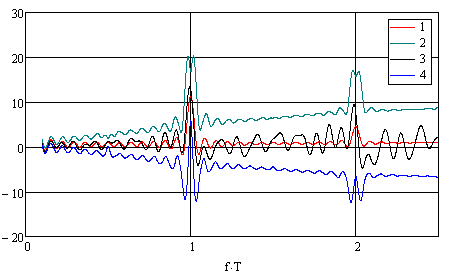
Рис. 2 Границы доверительной области косинус-преобразования потока с равномерной вобуляцией периода. N=15, δ=0.15. 1). Математическое ожидание. 2). Верхняя граница доверительной области. 3). Косинус-преобразование одной из реализаций потока. 4). Нижняя граница доверительной области.
Коэффициент периодичности
Из (5) следует, что
временному потоку (1) ставится в соответствие функция 
, определенная
в частотной области и равная сумме косинусоид с кратными частотами. Для строго
периодического потока (
) с нулевой эпохой при 
, а число синфазных
косинусоид в этой точке равно N-1[5]. Очевидно, что для -периодического
потока не все косинусоиды окажутся синфазными. Это приведет к тому, что при косинус-преобразование
будет меньше N-1. Тогда степень периодичности
потока можно оценить частным коэффициентом периодичности:
.
Для оценки свойств потока конкретного типа следует использовать средний коэффициент периодичности
.
Из (6) согласно определению (11) получаем выражение для коэффициента периодичности:
Рис. 3 Зависимость коэффициента периодичности от величины относительной девиации
На основании анализа результатов статистического
имитационного моделирования можно утверждать, что поток является -периодическим,
если его коэффициент периодичности не меньше 0.5. Тогда из (12)
получаем, что критическое значение относительной девиации периода равно 
=0.2215. На практике
предельное значение девиации не обязательно должно задаваться равным указанному.
Так, при жестких требованиях к точностным характеристикам разумно принимать меньше критического
значения.
Оценка периода потока
Рассмотрим две процедуры оценки периода. Первая является стандартной, применяемой при оценке среднего периода следования потока точек. Оценка равна:
где 
временное положение
первой и последней точек потока соответственно.
При равномерном распределении периода параметры оценки равны:
,
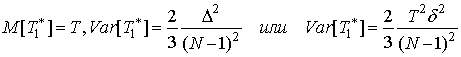где 
- дисперсия.
Оценка несмещенная и состоятельная как по ансамблю реализаций, так и по размеру N потока.
Вторая процедура оценки периода состоит в нахождении точки максимума косинус-преобразования (5):
где 
- корень уравнения 
.
Статистическое моделирование показало, что параметры оценки (14) не лучше, чем параметры оценки (13). Поэтому, учитывая простоту вычислений, целесообразно применять оценку (13).
Обнаружение периодичности
Найдя оценку периода по формулам (13) или
(14), наблюдатель не может судить о том, существует ли в потоке периодическая
составляющая. Действительно, длина потока 
и его размер N, используемые при вычислении оценки, не содержат
информации о внутренней структуре потока. Одно и то же значений оценки периода
можно получить как для строго периодического потока, так и совершенно
нерегулярного, например, пуассоновского. То есть, необходимо классифицировать
поток по уровню его периодичности, или, иначе обнаружить периодичность.
Процедура обнаружения базируется на
следующих рассуждениях. Допустим, что наблюдатель считает, что если относительная
вобуляция периода
меньше или равна критическому значению , то поток содержит периодическую
составляющую. В противном случае гипотеза о наличии периодичности отклоняется.
Критическому значению соответствует пороговое значение
коэффициента периодичности (12):
Тогда процедура обнаружения периодичности сводится к сравнению индивидуального коэффициента периодичности (10) с пороговым значением:
.
В качестве можно принять 
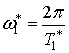или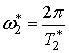 
. В первом случае
обнаружение производится по оценке периода (13), во втором –
по максимуму косинус-преобразования (14).
В результате статистического моделирования
найдены оценки вероятностей обнаружения для обоих вариантов задания . Параметры
потока варьировались в следующих пределах: N = 10, 20…50, = 0.05, 0.1…0.35, = 0.15, 0.2, 0.25. Оценки
усреднялись по 104 реализациям.
На рис. 4 приведены кривые вероятностей
обнаружения периодичности по максимуму косинус-преобразования, а на рис. 5 – по
оценке (13) периода. В обоих случаях допустимая
относительная девиация периода принималась равной 0.2.
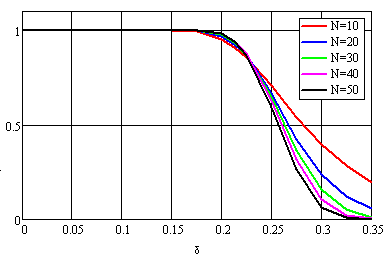
Рис. 4 Зависимость вероятности обнаружения периодичности от относительной вобуляции δ при оценке периода по максимуму косинус-преобразования. ZΔ0=0.56, δкр=0.204
Из сравнения графиков видно, что обнаружение по максимуму дает значительно лучшие результаты. Общим недостатком является то, что вероятности остаются достаточно большими и при вобуляции больше критической, что следует рассматривать как ложное обнаружение периодичности.
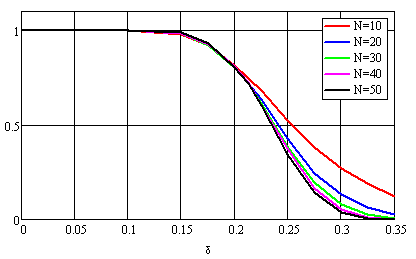
Рис. 5 Зависимость вероятности обнаружения периодичности от относительной вобуляции δ при оценке периода по формуле (13). ZΔ0=0.56, δкр=0.204
Вероятности обнаружения по максимуму косинус-преобразования достаточно надежно (коэффициент детерминации не меньше 0.992) аппроксимируются функцией:
где
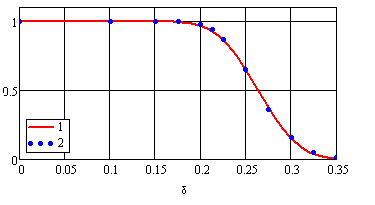
Рис. 6 Аппроксимация вероятности обнаружения периодичности при оценке периода по максимуму косинус-преобразования. N=30, δкр=0.2. 1). Аппроксимация. 2). Статистические данные.
Видно, что аппроксимирующая функция дает
несколько меньшие значения вероятности в области и при больших значения . Это
объясняется тем, что распределение косинус-преобразования в окрестности точки fT=1 отличается от нормального. Тем не менее, для
практических расчетов точность вполне приемлема, тем более что она возрастает с
увеличением N.
Вероятности ошибок обнаружения
Идеальная зависимость вероятности обнаружения от относительной девиации имеет вид:
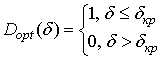
Если допустить, что относительная девиация равномерно
распределена на [0, 2], то вероятность необнаружения (пропуска)
равна:
. Аналогично, для вероятности ложного обнаружения можно записать:
. Выбор интервала усреднения [0, 2] обусловлен
тем, что при 
>0
и N>3 
, где 
- параметр нормальной плотности
распределения (18), являющийся среднеквадратическим
отклонением.
Вероятности ошибок зависят то N и 
. Размер N
потока после его регистрации известен. Поэтому вероятность ошибки можно
минимизировать, изменяя параметр .
Как следует из (17)
вероятность обнаружения равна функции надежности нормальной случайной величины.
Она нечетна относительно математического ожидания 
. Следовательно, вероятность
ошибки будет минимальна при 
. Из (19) получаем:
Подставив в (12) 
вместо , найдем
оптимальный порог для критерия (16):
.
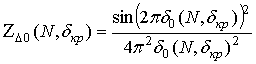На рис. 7 приведены кривые вероятности обнаружения при и N=10 и 40.
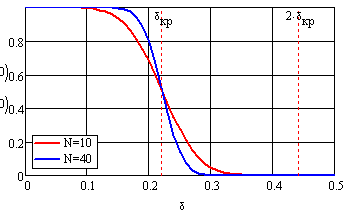
Рис. 7 Вероятность обнаружения периодичности потока с равномерной девиацией периода при оптимальном пороге обнаружения
График зависимости суммы вероятностей
пропуска (21) и ложного обнаружения (22) при
оптимальном пороге приведен на рис.9. Вероятность ошибки уменьшается с ростом
размера N потока и не зависит от критического значения
вобуляции
периода.
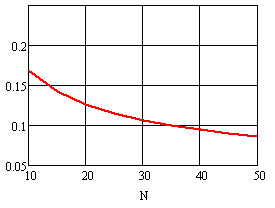
Рис. 8 Вероятность ошибки обнаружения периодичности потока с равномерной девиацией периода при оптимальном пороге обнаружения
По сравнению с типичными для радиолокации вероятностям ошибок, вероятности ошибки обнаружения периодичности выглядят чрезмерно большими. Однако необходимо учитывать следующие обстоятельства. Во-первых, процедура обнаружения периодичности носит вспомогательный характер. Чаще всего с ее помощью можно лишь получить дополнительную информацию, позволяющую повысить надежность принятия решения. Во-вторых, вероятность ошибки рассчитывалась в предположении, что поток априори обладает конкретными свойствами – его период вобулирован по закону равномерного распределения. Если окажется, что вместо ожидаемого потока будет предъявлен непериодический поток, например пуассоновский, то предложенная процедура обнаружения периодичности выявит это с высокой степенью надежности.
Периодический поток с нормальной вобуляцией периода
Рассмотрим поток, вобуляция периода которого
подчиняется нормальному распределению. Для корректного сравнения характеристик
данного потока с потоком с равномерной вобуляцией, положим, что дисперсии
периодов одинаковы. Тогда среднее квадратическое отклонение 
потока с нормальным
распределением периода можно выразить через относительную вобуляцию : 
или через полуинтервал
равномерного распределения 
.
Косинус-преобразование потока (3) равно
где – взаимно независимые
случайные величины, распределенные по нормальному закону с параметрами 
; - эпоха.
Математическое ожидание и дисперсия функции (23) равны соответственно:
где
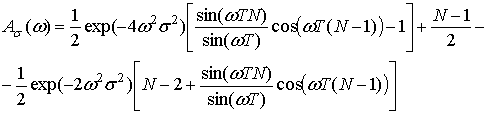
Функции 
определяются выражениями (8) и (9) соответственно.
Рис. 9. Математическое ожидание и среднее квадратическое отклонение косинус-преобразования потока. N =15, δ=0.15. 1). Математическое ожидание. 2). С.к.о.
Как и прежде, глобальный максимум среднего
значения косинус-преобразования находится в точке fT=1.
Значения функции 
распределены по нормальному закону за
исключением точки fT=1.
На рис. 10 изображены границы доверительного интервала при доверительной вероятности 0.997.
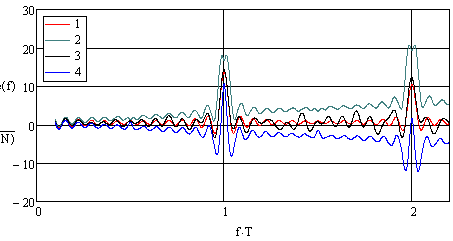
Рис. 10. Границы доверительной области косинус-преобразования потока с нормальной вобуляцией периода. N=15, δ=0.15. 1). Математическое ожидание. 2). Верхняя граница доверительной области. 3). Косинус-преобразование одной из реализаций потока. 4). Нижняя граница доверительной области.
Коэффициент периодичности
Выразив через и подставив в формулу (24) при 
, по аналогии с (11), получаем
выражение для коэффициента периодичности
На рис. 11 приведены графики коэффициентов периодичности потоков с равномерной и нормальной вобуляцией.
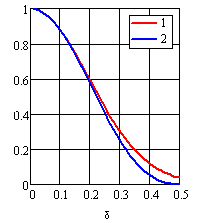
Рис. 11 Зависимость коэффициента периодичности потоков от относительной вобуляции. 1). Нормальная вобуляция. 2). Равномерная вобуляция.
Как и раньше, приняв минимально допустимое
значение коэффициента периодичности равным 0.5 из (26)
получаем, что критическое значение относительной девиации периода равно = 0.2295. Эта
величина несколько больше, чем для потока с равномерной вобуляцией (0.2215).
Оценка периода потока
В результате статистического моделирования выяснилось, что, как и для потока с равномерной вобуляцией, оценка периода по максимуму косинус-преобразования (23) имеет большую дисперсию, чем оценка (13).
Параметры оценки (13) равны:
.
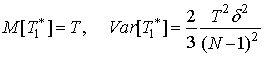Обнаружение периодичности
Процедура обнаружения периодичности подробно рассмотрена выше (см.).
Вероятность обнаружения по максимуму косинус-преобразования, как и прежде, аппроксимируется выражением (17) с параметрами:
,
.
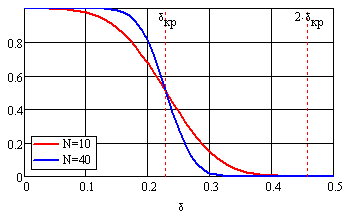
Рис. 12 Вероятность обнаружения периодичности потока с нормальной девиацией периода при оптимальном пороге обнаружения
Вероятности ошибок обнаружения
Вероятности пропуска и ложного обнаружения по-прежнему определяются формулами (21) и (22) соответственно.
На рис.13 приведены кривые вероятностей суммарной ошибки обнаружения периодичности для потоков с равномерной и нормальной вобуляцией в зависимости от размера N потока.
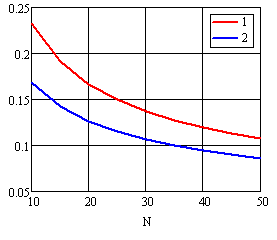
Рис. 13 Вероятность ошибки обнаружения периодичности потока с равномерной и нормальной девиацией периода при оптимальном пороге обнаружения. 1). Нормальная вобуляция. 2). Равномерная вобуляция.
Поток с накоплением дисперсии и нормальной вобуляцией
Поток данного типа представляет собой последовательность точек, паузы между которыми взаимно независимы и распределены по нормальному закону. Момент появления i-й точки равен сумме длительностей пауз между предшествующими i-1 точками. Моменты появления точек взаимно зависимы и их дисперсия растет с увеличением номера точки. Это позволяет заранее предположить, что коэффициент периодичности потока окажется меньше, чем для потоков рассмотренных выше.
Косинус-преобразование потока (3) равно
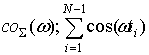
где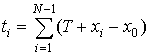 
, 
- взаимно независимые случайные величины с
распределением 
, - эпоха.
Момент возникновения i-й
точки распределен по закону 
. По-прежнему, для корректности сравнения
характеристик потоков разного типа принимаем , где - относительная девиация
периода T.
Можно показать, что среднее значение косинус-преобразования равно:
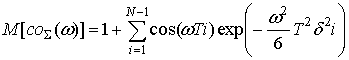(27).
График функции (27) приведен на рис. 14.
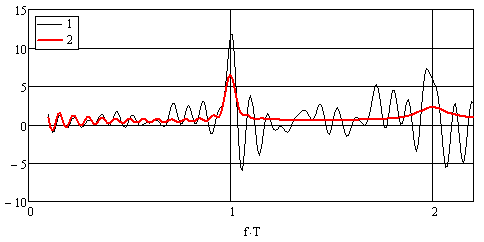
Рис. 14. Математическое ожидание и одна из реализаций косинус-преобразования потока. N =15, δ=0.15. 1). Математическое ожидание. 2). С.к.о.
Коэффициент периодичности
Подставив в (11) среднее
значение (27) косинус-преобразования при 
, получаем выражение для
коэффициента периодичности потока:
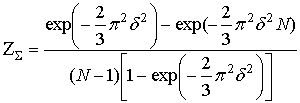
В отличие от потоков, рассмотренных ранее, коэффициент периодичности зависит от размера N потока. Он убывает с увеличением размера, что объясняется накопление дисперсии моментов возникновения точек. С ростом N уменьшается и критическое значение δкр относительной девиации, что приводит к ухудшению вероятностных характеристик обнаружения периодичности.
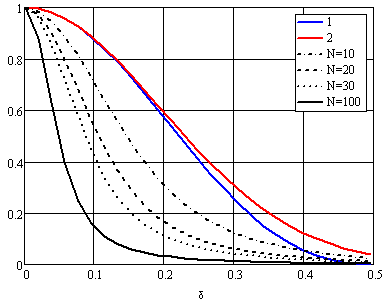
Рис. 15 Зависимость коэффициента периодичности потоков от относительной вобуляции. 1). Равномерная вобуляция. 2). Нормальная вобуляция. 3). Поток (3), N=10. 4). Поток (3), N=20. 5). Поток (3), N=30. 6). Поток (3), N=100.
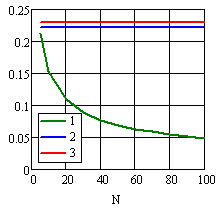
Рис. 16 Зависимость критического значения δкр коэффициента периодичности от размера N потока. 1). Поток с накоплением дисперсии. 2). Поток с нормальной вобуляцией. 3). Поток с равномерной вобуляцией.
Оценка периода потока
Как и прежде, оценка периода по максимуму косинус-преобразования имеет несколько худшие характеристики, чем оценка (13), которая для потока с накоплением дисперсии имеет следующие характеристики:
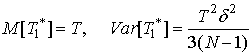
Оценка несмещенная и состоятельная по размеру потока.
Обнаружение периодичности
Для рассматриваемого потока процедура обнаружения периодичности, как и раньше (см.), состоит в сравнении частного коэффициента периодичности с порогом.
Вероятность обнаружения по максимуму
косинус-преобразования, как и прежде, аппроксимируется выражением вида (17). Однако вследствие зависимости 
от размера N потока, приходится находить коэффициенты
аппроксимирующих функций вида (19), (20)
для каждого конкретного значения N. По этой же
причине не удается получить универсальную формулу для оптимального порога.
Поэтому ограничимся иллюстрацией графиков зависимости вероятности обнаружения
периодичности для частных случаев (рис.17 ).
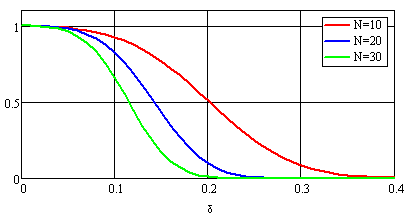
Рис.17. Вероятность обнаружения периодичности потока с накоплением дисперсии.
Из сравнения рис. 17 с рис. 7 и рис. 12 видно, что характеристики обнаружения периодичности потока с нормальным распределением интервалов хуже, чем для потоков с независимой девиацией периода. И это различие возрастает с увеличением размера потока.
Простейший (пуассоновский) поток
Для сравнения найдем характеристики потока, который заведомо не содержит периодической составляющей.
Интервалы между точками распределены по
экспоненциальному закону, а моменты 
возникновения точек имеют распределение
Эрланга i-го порядка.
Косинус-преобразование взвешенного [19] потока равно
Отметим, что начало интервала наблюдения можно принять равным нулю. При этом эпоха распределена по экспоненциальному закону, так же как и все интервалы между точками. Поэтому компенсация эпохи не требуется.
Усреднив по t и выполнив необходимые преобразования, получаем выражение для математического ожидания косинус-преобразования:
где - интенсивность потока, 
- число
сочетаний из n по m,
- целая
часть x.
Анализ выражения (29) показывает, что при =0 математическое
ожидание равно N, а при стремящемся к
бесконечности равно 0. При 
функция (29) не имеет заметных экстремумов
и практически равна нулю (рис. 16).
Дисперсия косинус-преобразования при хорошо
аппроксимируется выражением
На основании имитационного моделирования с
высокой надежностью можно утверждать, что при косинус-преобразование
пуассоновского потока распределено по нормальному закону 
. Тогда можно построить
доверительную область, график которой приведен на рис. 18.
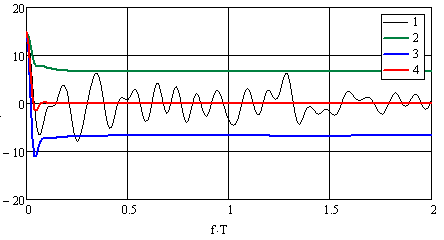
Рис. 18. Графики косинус-преобразования и границ доверительной области на уровне значимости 0.003 при N=15 и λ=1. 1). Случайная реализация косинус-преобразования. 2). Верхняя граница доверительной области. 3). Нижняя граница доверительной области. 4). Математическое ожидание косинус-преобразования.
Оценка периода потока
В данном случае речь идет об оценке
среднего интервала между точками. Для пуассоновского потока оценка (13) является максимально правдоподобной с параметрами: 
и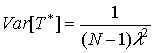 
.
Как и прежде, оценка несмещенная и состоятельная по размеру N потока.
Коэффициент периодичности
Математическое ожидание (29) косинус-преобразования равно нулю почти при всех значениях частоты f. Следовательно, коэффициент периодичности потока так же можно принять равным нулю.
Частный коэффициент периодичности пуассоновского потока равен
,
где 
.
Математическое
ожидание и дисперсия 
в соответствии с (29) и (30) равны 0 и 1/2N соответственно. Учитывая, что
при косинус-преобразование
распределено по нормальному закону, то и частный коэффициент периодичности имеет
нормальное распределение 
.
Обнаружение периодичности
Поскольку пуассоновский поток заведомо не содержит периодических составляющих, то факт обнаружения периодичности следует рассматривать как ложное событие.
Допустим, что наблюдатель принимает решение
о наличии периодичности в соответствии с критерием (16),
ожидая появления потока с равномерной вобуляцией при заданной относительной
вобуляции периода . Решение о наличии периодичности
подтверждается, если будет выполнено условие
, где 
, 
- порог (15).
Поскольку распределение частного коэффициента периодичности известно (см.), то вероятность обнаружения периодичности равна
.
Возможен иной подход к заданию порога обнаружения. Допустим, что для наблюдателя крайне нежелательно принятие решения о наличии периодического потока, когда на самом деле поток пуассоновский. В этом случае следует задать порог, гарантирующий получение вероятности ложного обнаружения на заданном уровне, например 1.5*10-3, при котором порог обнаружения равен трем стандартным отклонениям (см.):
.
На рис. 19 приведены графики зависимости
вероятности обнаружения периодичности пуассоновского потока при = 0.15, 0.2 и
0.25 и пороге (34), гарантирующем заданную вероятность обнаружения при любом
размере N потока.
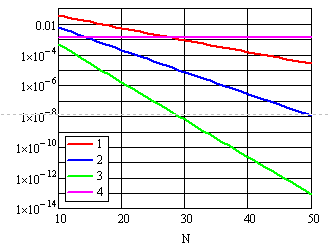
Рис. 19. Зависимость вероятности ложного обнаружения периодичности от размераN потока при различных критических значениях относительной девиации. 1). δкр =0.25. 2). δкр =0.2. 3). δкр =0.15. 4). Переменный порог (34).
Видно, что вероятность ложного обнаружения периодичности значительно меньше вероятности правильного обнаружения потоков с равномерной вобуляцией и быстро убывает с увеличением размера потока.
Заключение
Дано определение -периодического потока и
предложена процедура обнаружения периодичности, которая сводится к вычислению
косинус-преобразования потока (например[6],
(5)), отысканию его максимума, расчету частного коэффициента
периодичности (10) и сравнению его с порогом (15).
Методом имитационного статистического
моделирования найдены зависимости вероятности обнаружения периодичности от
относительной девиации периода и размера потока N. Определено значение оптимального порога, удовлетворяющее
критерию идеального наблюдателя.
Практика применения предложенного метода состоит в следующем:
- наблюдатель задает предельное значение
девиации 
периода,
при котором поток можно считать -периодическим;
- в зависимости от априорных сведений о виде закона распределения девиации, выполняются необходимые расчеты, на основании которых реализуется процедура обнаружения периодичности.
Предложенная методика обнаружения периодичности потоков может найти применение в системах пассивной радиолокации и системах радионаблюдения, а также в прикладных задачах, связанных с исследованием свойств случайных потоков.
Следует отметить, что полученные результаты справедливы для потоков, эпоху которых можно компенсировать путем сдвига начала интервала наблюдения в первую точку потока. Если исследуемый процесс является суперпозицией потоков, то предложенную методику можно применять, если число перекрывающихся во времени потоков достаточно велико и результирующий поток близок по своим свойствам к пуассоновскому. В этом случае можно говорить лишь об «обнаружении» отсутствия периодичности.
Литература
1. Риордан Дж. Вероятностные системы обслуживания. - М.: Связь, 1966. - 184 с.: ил.
2. Саати Т. Л. Элементы теории массового обслуживания и ее приложения. - М.: Сов. радио. 1971, - 520 с.: ил.
3. Кокс А., Льюис П. Статистический анализ последовательности событий. – М.: Мир, 1969. – 312 с.: ил.
4. Калашников В. В., Рачев С. Т. Математические методы построения стохастических моделей обслуживания. – М.: Наука, 1988. – 312 с.: ил
5. Надежность технических систем: Справочник / Ю. К. Беляев, В. А. Богатырев, В. В. Болотин и др.; Под ред. И. А. Ушакова. – М.: Радио и связь, 1985. – 606 с., ил.
6. Большаков И. А. Статистические проблемы выделения сигналов из шума. – М.: Сов. радио, 1969. – 464 с., ил.
7. Большаков И. А., Ракошиц В. С. Прикладная теория случайных потоков. – М.: Сов. радио, 1978. – 248 с., ил.
8. Тихонов В. И. Статистическая радиотехника. – М.: Сов. радио, 1966. – 678 с.: ил.
9. Тихонов В. И., Харисов В. Н, Статистический анализ и синтез радиотехнических устройств и систем: Учебное пособие для вузов. – М.: Радио и связь, 1991. – 608 с.: ил.
10. Тихонов В. И., Хименко В. Н. Выбросы траекторий случайных процессов. М.: Наука, 1987.
11. Фомин Я. А. Теория выбросов случайных процессов. М.: Связь. 1980г. 216 с., ил.
12. Лабунец Л. В. Оценка распределения длительности выбросов одного класса негауссовских случайных процессов. / М.: Радиотехника.- 1986. - № 9. - С. 64-67 .
13. Лабунец Л. В. Распределение длительности выбросов нестационарного нормального процесса. /М.: Радиотехника. - 1985. - № 11. - С. 47-50.
14. Билык М. Г. О потоках пересечений постоянного уровня нестационарными процессами/ Отбор и передача информации, № 48, 1976
15. Билык М. Г. О некоторых характеристиках пересечений случайных процессов. /Отбор и передача информации, № 59, 1980
16. Серебряков М.Г., Первозванский А.А. Выявление скрытых периодичностей. - М.: Наука, 1965. - 244 с.
17. Харкевич А. А. Спектры и анализ. - М..: Госиздат физико-математической литературы, 1962. – 236 с.: ил.
18. Седякин Н. М. Элементы теории случайных импульсных потоков. - М.: Сов. радио, 1965. - 261 с.
19. Голик Ф. В., Порхунов Е. А. Периодический поток со случайной независимой децимацией. /Журнал радиоэлектроники, № 10, 2008. http://jre.cplire.ru/jre/oct08/index.html.
[1] Для определенности обычно указывают направление движения процесса – снизу вверх или сверху вниз.
[3] Термин наш.
[5] Вследствие компенсации эпохи, точка t1=0 и вклад первой косинусоиды в сумму (5) равен 1 при всех частотах.
[6] Здесь и далее даны ссылки на формулы, полученные для потока с равномерной девиацией периода.
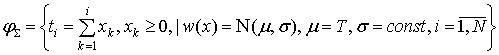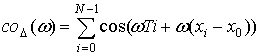
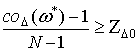
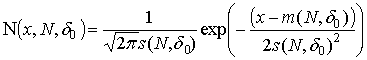
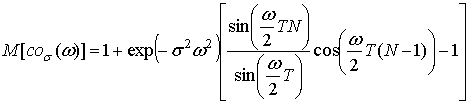
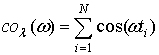
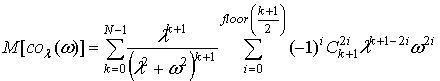
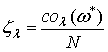
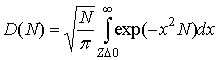
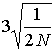