УДК 621.296.67

Моделирование СКАНИРУЮЩЕЙ ГИБРИДНОЙ ЗЕРКАЛЬНОЙ АНТЕННЫ С МАЛЫМ ШАГОМ ПЕРЕМЕЩЕНИЯ ЛУЧА

 

А. Н. Пластиков ^1,2, Н. М. Фейзулла ¹

 

¹ ОАО "ОКБ МЭИ"

² Национальный исследовательский университет Московский энергетический институт, кафедра Антенных устройств и распространения радиоволн

 

Получена 27 мая 2012 г.

Аннотация. Рассмотрена симметричная параболическая сканирующая зеркальная антенна S-диапазона с облучателем в виде решетки Н-секториальных рупорных антенн. Основное внимание уделено численному исследованию радиотехнических характеристик облучателя. Оптимизирована конструкция элементов решетки с целью совмещения фазовых центров в плоскостях векторов Е и Н. Сопоставлены диаграммы направленности, рассчитанные как при непосредственном моделировании всех излучающих элементов решетки, так и полученные с использованием множителя комбинирования для уединенного элемента и элемента в составе бесконечной решетки. Определены диаграммы направленности вторичного поля излучения. Рассчитан коэффициент отражения на входе делителя мощности, обеспечивающего синфазное и равноамплитудное возбуждение излучающих элементов решетки.

Ключевые слова: гибридная зеркальная антенна, антенная решетка, рупорная антенна, облучатель, фазовый центр, множитель комбинирования, периодические граничные условия.

Abstract. S-band scanning prime focus parabolic reflector antenna with H-plane sectorial horn array feed is presented in this article. Calculations were made by the use of method of moments code. Horn design was optimized for obtain overlapping phase centers in E- and H-planes. Far fields were comparing for three different models: first design include directly all radiating horns while the rest use array factor for one horn in free space and one horn formed part of infinite array. The reflection factor for power divider provided an in-phase and equal amplitude excitation of array elements is determined.

Index terms: array-fed reflector antenna, antenna array, horn antenna, primary antenna feed, phase center, array factor, periodic boundary conditions.

 

         Введение

         Для однозеркальной АС существуют два принципиальных подхода к обеспечению режима сканирования диаграммой направленности (ДН). Первым из них является механическое перемещение облучателя. Второй вариант подразумевает использование облучающей антенны с изменяемым амплитудно-фазовым распределением в его раскрыве и зачастую реализуется в виде облучающей фазированной антенной решетки. В этом случае саму АС принято называть гибридной зеркальной антенной (ГЗА).

         В качестве облучателей ГЗА достаточно широкое распространение получили различные варианты решеток на базе рупорных антенн. Простейшим вариантом подхода к построению подобной сканирующей облучающей решетки может являться использование для формирования каждого из лучей своей отдельной рупорной антенны, при этом переключение лучей можно производить посредством диаграммообразующей схемы (ДОС) на основе СВЧ переключателей мощности. Существенным недостатком подобного подхода является относительно большой шаг отклонения луча, который для фиксированного зеркала определяется главным образом габаритами раскрыва рупора.

         В работе рассмотрен вариант реализации облучателя симметричной параболической ГЗА S-диапазона в виде решетки H-секториальных рупорных антенн, позволяющей осуществлять сканирование с малым шагом отклонения луча. Описан принцип построения облучающей системы. Основное внимание уделено расчету и оптимизации характеристик излучения модели рупорной решетки. Приведены также результаты расчета ДН всей АС.

        

         Описание рупорного облучателя

         Схема построения рассматриваемой конструкции рупорного облучателя представлена на рис. 1. Сама решетка H-секториальных рупорных антенн включает в себя в общем случае N∙M элементов. Непосредственно излучать могут только N соседних  рупоров, которые возбуждаются синфазно и образуют таким образом излучающий кластер. За счет перемещения этого излучающего кластера вдоль всей решетки удается осуществлять однокоординатное управление ДН зеркальной антенной системы (обеспечить отклонение направления главного лепестка ДН от оси системы). При этом шаг изменения положения (сдвига) кластера равен ширине раскрыва одного рупора, величина которой относительно мала и выбирается исходя из требования на шаг отклонения ДН АС. 

  

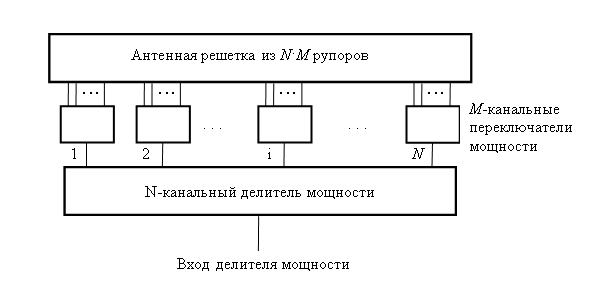
Рис. 1. Схема построения облучающей рупорной решетки

 

         ДОС антенной решетки включает в себя делитель мощности на N-каналов, N M-канальных СВЧ переключателей мощности, выходы которых подключаются ко входам антенных элементов решетки в определенном порядке, образуя таким образом матрицу подключений. При этом числа N и M выбираются исходя из требуемой ширины ДН облучателя в плоскости вектора E и заданной ширины сектора сканирования. Схемы СВЧ переключателей, входящих в состав ДОС, можно строить, например, на основе PIN-диодов.

         Для совмещения положения фазовых центров в плоскостях векторов Е и Н кластеров в конструкции облучателя производится срез широких стенок рупоров (см. рис. 2), что позволяет улучшить сферичность фазовой характеристики поля излучения. Так как подобная антенна не имеет фазового центра (ФЦ) в строгом понимании этого определения, то здесь и далее мы будем говорить о частичных фазовых центрах [1], относительно которых фазовая характеристика близка к постоянной (с учетом весовой функции в виде амплитудной ДН) в пределах углов облучения зеркала, в двух главных плоскостях. На рис. 3 отображена фотография участка раскрыва реального облучателя подобной конструкции.

 

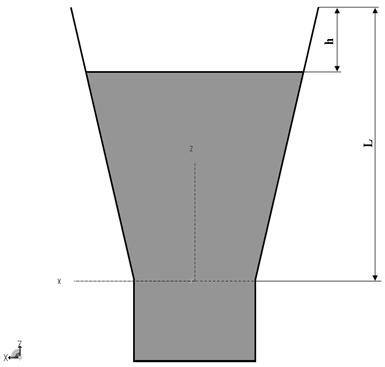
Рис. 2. Геометрия модели антенного элемента облучателя в Н-плоскости (с использованной при расчетах системой координат)

 

Рис. 3. Фотография части изготовленного облучателя

 

          Моделирование облучателя. Оптимизация конструкции с целью совмещения фазовых центров

         Приведем результаты численного исследования облучателя рассмотренной конструкции, спроектированного для работы в составе АС с симметричной параболической зеркальной антенной диаметром раскрыва D около 70∙λ (λ  – длина волны) и отношением фокусного расстояния F к диаметру D около 0,6. Соответствующий угол, под которым из фокуса виден край зеркала, равен

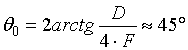.                                     (1)

 

Зададимся для примера числом N рупоров в активном кластере, равным 8. Моделирование соответствующей решетки H-секториальных рупоров проводилось посредством метода моментов на уровне одного кластера. На рис. 4 изображена модель анализируемой структуры антенны, представляющая собой кластер из 8 рупоров, возбуждаемых равноамплитудно и синфазно. Элементы решетки возбуждались с помощью волноводных портов. Металлические поверхности задавались как идеальный проводник.

 

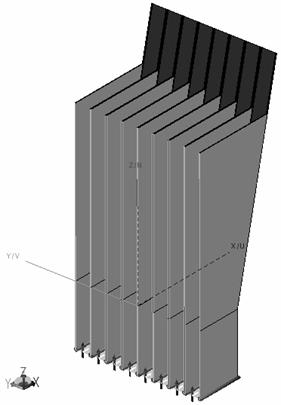
Рис. 4. Модель кластера из 8-ми рупоров в разрезе

 

         Размеры рупорной части и ширина узкой стенки волновода были подобраны из условия обеспечения максимальной величины коэффициента использования поверхности зеркала при отсутствии среза широкой стенки рупоров, т.е. для случая h=0. Задачей дальнейшей оптимизации было исследовать влияние глубины среза h на положение ФЦ в обеих плоскостях и определить таким образом окончательную геометрию облучателя, позволяющую совместить оба ФЦ.

Полученная зависимость координат ФЦ в плоскостях векторов Е и Н (относительно отображенного на рис. 1, 3 положения начала системы координат) в зависимости от h приведена на рис. 5. Оси абсцисс и ординат нормированы на высоту рупорной части L (см. рис. 1), которая для рассматриваемой решетки равна около 1,8∙λ. Соответствующий график позволяет заключить, что проводимый срез рупоров в Н-плоскости существенно влияет только на положение ФЦ кластера в Е-плоскости. При этом координата ФЦ кластера в Е-плоскости все время располагается немного ниже уровня среза стенки рупоров, отмеченного на рис. 5 штриховой прямой линией. Совпадение ФЦ происходит при глубине среза h ≈ 0,04∙L, что соответствует точке пересечения двух кривых рис. 5. Соответствующая координата ФЦ по оси z равна примерно z_ФЦ = 0,9∙L. Обращает на себя внимание изменение монотонного хода графиков вблизи точки совмещения ФЦ.

 

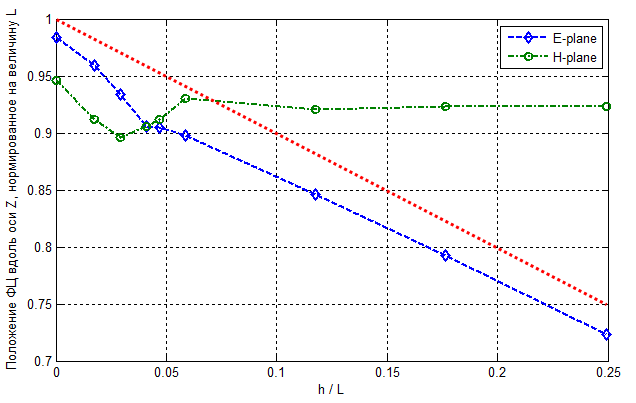
Рис. 5. Положение фазового центра в зависимости от глубины среза рупоров

 

Заметим, что проведенный анализ одного уединенного элемента (рупора) кластера показал совпадение положения обоих ФЦ при глубине среза h ≈ 0,24∙L. При этом, как видно из рис. 5, ФЦ решетки таких рупоров (кластера) не совпадают и расходятся примерно на одну треть длины волны. Изменение положения фазовых центров при переходе от одного рупора к кластеру из восьми элементов обусловлено взаимным влиянием антенных элементов.

         Рассчитанные фазовые ДН для оптимизированного кластера с синфазно возбуждаемыми рупорами в Е- и Н-плоскостях приведены на рис. 6 в декартовой системе координат в секторе углов  |θ| ≤ 80°. На данном рисунке изображены зависимости, соответствующие трем положениям системы координат начала отсчета фазы: в рассчитанной точке положения фазового центра (0, 0, z_ФЦ), а также двум точкам, соответствующим 5% отклонению от z_ФЦ как в большую, так и в меньшую стороны, что эквивалентно около 0,08∙λ (напомним, что координата z отсчитывается от плоскости начала излома рупоров). Пологий характер характеристик, соответствующих точке (0, 0, z_ФЦ), подтверждает отмеченный на рис. 5 результат совмещения ФЦ кластера в двух плоскостях.

 

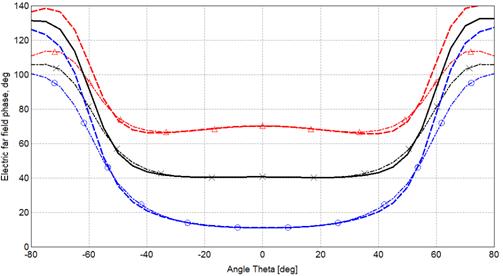
Рис. 6. Фазовые характеристики электрического поля кластера в дальней зоне:

 

На рис. 7 отображены рассчитанные нормированные амплитудные кополяризационные ДН кластера в полярной системе координат в плоскостях векторов Е и Н, где для сравнения приведены также и соответствующие ДН одного уединенного рупора из состава кластера. На этом же рисунке отображена и ДН кроссполяризационной составляющей поля излучения кластера в плоскости φ = 45° (D-плоскости). Помимо очевидного сужения главного лепестка ДН в Е-плоскости при переходе от одного уединенного рупора к многоэлементной решетке обращает на себя внимание видоизменение формы ДН в Н-плоскости, которое нельзя предсказать при использовании множителя комбинирования для расчета поля излучения решетки по известной ДН одного уединенного элемента. Рассчитанный коэффициент направленного действия кластера равен 12,9 дБ. Полезная и паразитная составляющие поляризации определялись в соответствии с так называемым третьим определением Людвига [2].

 

 

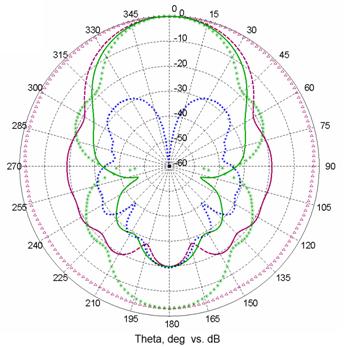
Рис. 7. Нормированные диаграммы направленности одного уединенного рупора и решетки из синфазно возбуждаемых 8-ми рупоров в полярной системе координат в логарифмическом масштабе:

 

         В процессе проведенных исследований была также рассмотрена модель кластера, включающая в себя помимо возбуждаемых рупоров также и несколько соседних с ними неизлучающих элементов решетки. ДН кластера при этом меняются несущественно, если эти неизлучающие элементы расположены симметрично относительно кластера, по обе стороны. Однако для кластера, расположенного на краю всей решетки рупоров, характерной чертой является возникновение асимметрии ДН в Е-плоскости. Далее мы будем говорить о рассматриваемой антенной решетке в контексте результатов, полученных для уединенного кластера.

 

           Сравнение трех способов расчета поля излучения кластера

         Известно, что поле излучения антенной решетки можно рассчитать с использованием так называемого множителя комбинирования или множителя направленности [1] путем его перемножения с ДН одного элемента решетки. При этом в качестве последней можно взять как, например, просто ДН одного уединенного элемента решетки, так и воспользоваться результатом расчета поля излучения одного элемента в составе бесконечно протяженной решетки. Последнее возможно реализовать в современных программных комплексах проектирования антенн и устройств СВЧ при введении в модель одного элемента решетки так называемых периодических граничных условиях (periodic boundary conditions), в частности, используя разложение по гармоникам Флоке [3]. Сравним соответствующие варианты расчета поля излучения с результатами, полученными при анализе непосредственно кластера.

         Для рассматриваемой эквидистантной решетки синфазно и равноамплитудно возбуждаемых рупоров множитель комбинирования в плоскости решетки (Е-плоскости) определяется выражением

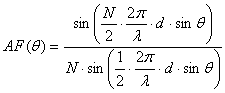 ,                                     (2)

где d – шаг решетки.

         На рис. 8 представлены амплитудные ДН, полученные тремя различными способами: рассчитанные по полям излучения одного уединенного рупора и одного элемента бесконечной решетки с последующим пересчетом ДН решетки  с использованием множителя комбинирования (для плоскости вектора Н последний тождественно равен единице), а также посредством моделирования непосредственно всего кластера. Полученные различия графиков позволяют заключить, что в пределах углов θ ≤ 40...50º расчет с использованием периодических граничных условий (ПГУ) позволил получить ДН, близкие к расчету непосредственно всего кластера. В пределах этих же углов расчет, проведенный с использованием поля излучения одного уединенного элемента и множителя комбинирования решетки, дает существенно искаженный результат в Е-плоскости. Большая погрешность подобного расчета вполне ожидаема вследствие близкого расположения антенных элементов решетки.

 

а)	б)
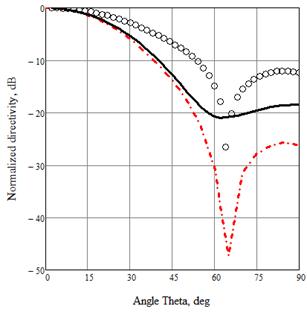
Рис. 8. ДН решетки рупоров в плоскостях векторов Е (а) и Н (б), рассчитанные различными способами:

        

          О согласовании элементов антенной решетки

         Остановимся на вопросе определения качества согласования кластера. В рассчитанной матрице S-параметров оптимизированной антенной решетки обращают на себя внимание высокие уровни модулей коэффициентов отражения волноводных портов |S_kk| ≈ 0,94÷0,96 ,  k = 1, 2, … 8. Это связано с тем, что каждый рупор имеет достаточно маленькую ширину узкой стенки волновода b (по сравнению с длиной волны), а в сечении такого волновода  с волной Н₁₀ велико отражение. Увеличение ширины этой узкой стенки должно приводить к существенному падению модуля коэффициента отражения [4].

В сечении волноводов весь наш кластер – совокупность N прямоугольных волноводов, в которых распространяется волна Н₁₀, можно рассматривать как один непрерывный волновод с волной Н₁₀, ширина которого в Е-плоскости равна примерно N∙b. Вследствие этого на входе делителя мощности, где (в режиме приема) синфазно суммируются поля ото всех антенных элементов кластера, следует ожидать существенного снижения уровня отраженной волны по сравнению с |S_kk|. Именно эти соображения и были положены в основу конструктивного исполнения рассматриваемого облучателя. Проверим данные суждения, обработав рассчитанную матрицу S-параметров модели кластера.

Элементы вектора-столбца S-параметров S_i в сечениях входов элементов кластера (волноводных портов) для случая одновременного синфазного возбуждения всех 8-ми рупоров могут быть найдены на основе соотношений

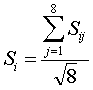 , i = 1, 2 …8  ,                                    (3)

 

где S_ij  – элементы исходной S-матрицы размера 8х8, а множитель 8^-1/2  введен для нормировки всей мощности на единицу. Тогда коэффициент отражения S_д на входе делителя в приближении равноканального деления мощности и отсутствия потерь в ДОС определяется выражением

.                                                  (4)

Заметим, что более общие соотношения для расчета согласования многоэлементных антенн с учетом схемы питания приведены, например, в [3,5].

На основании выражений (3), (4) и рассчитанной S-матрицы кластера мы получили модуль | S_д | ≈ 0,14 ,  что соответствует коэффициенту стоячей волны около 1,3 и уровню отраженной мощности около 2%. Таким образом, на входе делителя мы действительно имеем достаточно неплохое согласование, что свидетельствует о правильности приведенных выше соображений.

 

         Вторичное поле излучения ГЗА

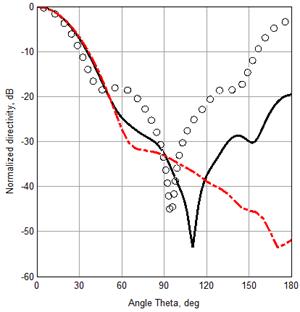
Расчет вторичного поля излучения всей антенной системы был проведен методом физической оптики при задании самого облучателя – кластера в виде точечного источника поля, помещенного в фокус зеркала. Ширина ДН зеркальной антенны по уровню -3 дБ составила около 1º. На рис. 9 представлены ДН вторичного поля излучения антенной системы, рассчитанные для четырех положений кластера в решетке: в центре решетки (центральный луч), со смещением offset центра кластера в фокальной плоскости из фокуса на d, 8·d и 16·d.

 

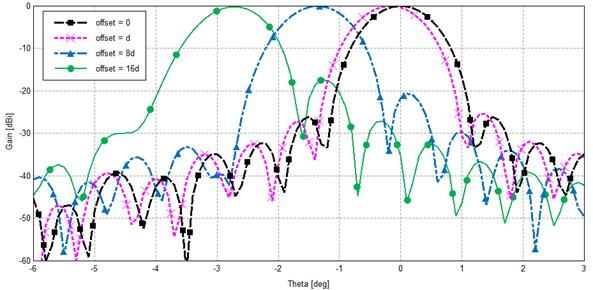
Рис. 9. Нормированные ДН антенной системы при сканировании

 

Максимальное снижение усиления, обусловленное выносом кластера (его ФЦ) из фокуса, составило 0,2 дБ. Однако за счет возникновения несимметричных аберраций типа комы при этом рост уровня бокового излучения относительно центрального луча составляет около 10 дБ. Отметим, что за счет смещения кластера удается обеспечить отклонение максимума луча системы примерно на 0,17º на каждый шаг решетки d. При этом если бы мы взяли в качестве одного активного кластера один рупор, раскрыв которого в Е-плоскости соответствует величине N∙d, то шаг отклонения луча ДН был бы примерно в N раз больше (см. рис. 9 для случая offset = 8·d).

 

         Заключение

         Таким образом, посредством метода моментов проведено исследование антенной решетки облучателя ГЗА S-диапазона, составленной из Н-секториальных рупоров. Конструкция решетки оптимизирована с целью совмещения фазовых центров в плоскостях векторов Е и Н.

         Инженерная оценка характеристик излучения решетки через множитель комбинирования и известную ДН одного уединенного элемента в рассматриваемой задаче не позволила получить результатов приемлемой точности (как с точки зрения амплитудных ДН, так и с точки зрения положения фазового центра в двух плоскостях). Использование для этой цели расчета с введенными ПГУ, наоборот, позволило достаточно точно определить ДН решетки в пределах углов облучения зеркала.

         Отмечено, что вследствие малой ширины узкой стенки волновода согласование каждого отдельного рупора является посредственным, однако в сечении входа делителя мощности модуль коэффициента отражения всей решетки (кластера) достаточно мал.

         Методом физической оптики рассчитаны ДН вторичного поля излучения АС и определен возможный шаг отклонения луча при электрическом сканировании, который для рассматриваемой АС с апертурой 70 длин волн составил немного более 1/6 ширины ДН по уровню -3 дБ.  

 

Литература

1.     Марков Г.Т., Сазонов Д.М. Антенны. Учебник для радиотехнических специальностей вузов. Изд. 2-е, перераб. и доп. М.: Энергия, 1975.

2.     Ludwig A.C. The Definition of Cross Polarization // IEEE Transaction on Antennas and Propagation. 1973. V. 21. P. 116-119.

3.     Банков С.Е., Курушин А.А. Электродинамика и техника СВЧ для пользователей САПР. – М., 2008 (электронная версия: http://jre.cplire.ru/jre/library/3/text.pdf).

4.     Вайнштейн Л.А. Теория дифракции и метод факторизации. – М.: Советское радио, 1966.

5.     Банков С., Давыдов А., Курушин А. Проектирование многоэлементных антенн со сложными системами питания. EDA Express №16, 2007, с. 23-29.