Обработка эхосигналов группового объекта методами сверхрэлеевского разрешения по дальности и скорости на основе экспериментальных данных

УДК 621.396.962

Д. С. Григорян, С. А. Климов, Д. Г. Митрофанов, А. Г. Прохоркин

лаборатория проблем обработки радиолокационной информации военной академии войсковой ПВО
имени маршала Советского Союза А. М. Василевского, Смоленск

Получена 15 июня 2012 г.

Аннотация. Представлены результаты обработки эхосигналов квазинепрерывного излучения и с линейной частотной модуляцией радиолокационной станцией, сопровождающей групповой воздушный объект. Экспериментально подтверждена возможность сверхрелеевского разрешения групповых объектов по дальности и скорости в импульсном объеме классическими и когерентными методами авторегрессионного цифрового спектрального анализа, а также методами, основанными на теории статистических решений. Приведены особенности сверхрэлеевского разрешения эхосигналов после предварительной цифровой обработки сигналов в условиях их искажений в приемо-передающем тракте РЛС, взвешивания огибающей пачки импульсов во времени, отражений от подстилающей поверхности, местных предметов и винтовых составляющих.

Ключевые слова: сверхрэлеевское разрешение, групповой воздушный объект, линейное предсказание, теория статистических решений, линейная частотная модуляция, вектор весовых коэффициентов, временная функция, спектральная функция, строб дальности, частотный фильтр.

Abstract. Results of processing of signals of quasicontinuous radiation and with linear frequency modulation by the radar station accompanying group air object are presented. Possibility of superresolution of group objects on range and speed in pulse volume is experimentally confirmed with classical and coherent methods of the autoregression digital spectral analysis, and also the methods based on the theory of statistical decisions. Features of superresolution of signals after preliminary digital processing of signals in the conditions of their distortions are given in a send-receive path of RLS, weighing of a bending-around pack of impulses in time, reflections from a spreading surface, local subjects and screw components.
Keywords: superresolution, group air object, linear prediction, theory of statistical decisions, linear frequency modulation, vector of weight factors, time function, spectral function, range strobe, frequency filter.

Введение

Достигнутый прогресс в области методов цифровой обработки сигналов и радиолокационной системотехники позволяет существенно улучшить характеристики разрешающей способности радиолокационных систем различного назначения за счет внедрения на программном или аппаратно-программном уровне алгоритмов сверхрэлеевского разрешения эхосигналов по дальности и скорости.

В настоящее время сформировались различные направления развития методов обработки сигналов со сверхрэлеевским разрешением. Первое направление – это авторегрессионные методы цифрового спектрального анализа, исходные (классические) подходы которого обобщены в [1] и [2]. Их анализ свидетельствует о большом количестве последователей методов цифрового спектрального анализа по всему миру.

Вторым, одним из интенсивно развивающихся направлений, можно считать авторегрессионный спектральный анализ с когерентными методами предварительной обработки данных. В основе данного направления лежат авторегрессионные параметрические методы теории многоканального анализа. Они представлены в работах [3–6].

Третье направление это методы, сводящие решение задачи сверхрэлеевского разрешения сигналов к развитию тем или иным образом традиционных (классических) методов обработки, в основе которых лежат достаточно многочисленные модификации алгоритмов статистических решений: байесовских, максимального правдоподобия и наименьших квадратов [7–20].

Одним из главных вопросов на сегодняшний день является вопрос о практической применимости методов сверхрэлеевскго разрешения в радиолокационных станциях (РЛС) и системах на этапе первичной обработки радиолокационной информации. Несмотря на очевидную теоретическую возможность их реализации, многие разработчики указывают на принципиальные трудности, связанные с искажениями временной и частотной структуры сигналов в приемо-передающих трактах РЛС, влиянии подстилающей поверхности и т. д., не позволяющие эффективно применять алгоритмы сверхрэлеевского разрешения в РЛС. Следовательно, для подтверждения практической возможности сверхрэлеевского разрешения групповых воздушных объектов в реальных условиях эксплуатации РЛС целесообразно проведение натурного эксперимента.

Целью работы является подтверждение практической возможности сверхрэлеевского разрешения по дальности и скорости сигналов, отраженных от парного группового воздушного объекта, сопровождаемого реальной РЛС в когерентно-импульсном и импульсно-доплеровском режимах работы в условиях искажений временной и частотной структуры сигналов в приемо-передающих трактах РЛС.

Условия проведения эксперимента

Эксперимент с групповым воздушным объектом проводился при участии сотрудников НИИ радиоэлектронной техники МГТУ им. Н. Э. Баумана: С. Нефедова, Г. Слукина, И. Крючкова и В. Шустикова и по разработанной ими методике. В качестве группового воздушного объекта использовались два спортивных самолета Як-52 из смоленского аэроклуба ДОСААФ, которые должны были двигаться в паре по указанному маршруту на расстоянии друг от друга от 25 до 75 м [21]. Самолеты двигались на высотах от 500 м до 1 км. Дальности до позиции РЛС по маршруту следования самолетов составляли от 2 км до 26 км с южного направления от учебного полигона.

В качестве радиолокатора, сопровождавшего групповой воздушный объект, использовалась многофункциональная РЛС, размещенная на учебном полигоне (г. Смоленск, пос. Дубровенка). При сопровождении самолетов РЛС поочередно работала в импульсном режиме масштаба 50 км с использованием радиоимпульса длительностью 50 мкс с линейной частотной модуляцией (ЛЧМ) с девиацией частоты 900 кГц и скважностью 10, а также в режиме квазинепрерывного излучения (КНИ) простых радиоимпульсов длительностью 2,5–7 мкс и скважностью 10.

В первом режиме в приемной системе РЛС с помощью дисперсионной ультразвуковой линии задержки (ДУЛЗ) формируются радиоимпульсы с ЛЧМ на промежуточной частоте 10 МГц, после чего с помощью системы гетеродинов переносятся на первую промежуточную частоту 28 МГц. Импульсы с ЛЧМ, проходя транзитом когерентный гетеродин (КГ) и смешиваясь в усилительной цепочке передатчика с сигналом одного из клистронных задающих генераторов с частотой -28 МГц (рис. 1), переносятся на несущую частоту и, усиливаясь в клистронном усилителе с импульсным модулятором, излучаются антенно-волноводной системой в пространство.

Рис.1. Упрощенная функциональная схема приемо-передающей части РЛС

с подключением АЦП (цифрами 1, 2 и 3 показаны тройник, АЦП и ПЭВМ,

введенные в состав РЛС во время эксперимента)

При приеме, отраженный от воздушного объекта сигнал с частой (– частота Доплера), усиленный лампой бегущей волны, с помощью сигнала -28 МГц преобразуется в приемной системе на первую промежуточную частоту 28 МГц и усиливается в предварительном усилителе промежуточной частоты (ПУПЧ). К выходу ПУПЧ в ходе эксперимента был подключен коаксиальный тройник, с помощью которого часть энергии сигнала отводилась в плату сбора данных, основным узлом которой являлся аналогово-цифровой преобразователь (АЦП), работающий с тактовой частотой 60 МГц. В плате сбора данных осуществлялось преобразование сигнала в цифровую форму, цифровое преобразование вниз с децимацией таким образом, чтобы частота следования данных на выходе платы составляла 1,9 МГц с учетом девиации частоты ЛЧМ сигнала 900 кГц для соблюдения условий теоремы Котельникова.

Во втором режиме усиление, преобразование и прием-передача сигналов происходит в том же порядке за исключением того, что вместо ДУЛЗ для получения колебаний промежуточной частоты используется сам КГ (см. рис. 1).

При сопровождении объектов РЛС переключалась из одного режима излучения в другой, а плата сбора данных передавала оцифрованные сигналы ЛЧМ и КНИ с частотой 1,9 МГц для записи в асинхронном режиме прямого доступа в память персональной электронно-вычислительной машины (ПЭВМ), находящейся в аппаратном отсеке. Так была осуществлены записи сигналов пары воздушных объектов (рис. 2, 3) длительностью до трех минут каждая на дальностях от 2 до 29 км в режимах ЛЧМ и КНИ.

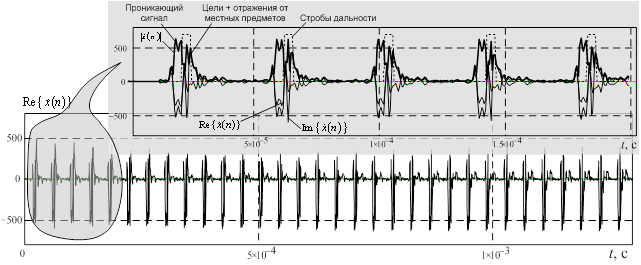
Рис. 2. Фрагменты записи сигналов РЛС, отраженных от двух самолетов Як-52,

взятых на сопровождение на дальности 29 км и азимуте 145º в режиме КНИ

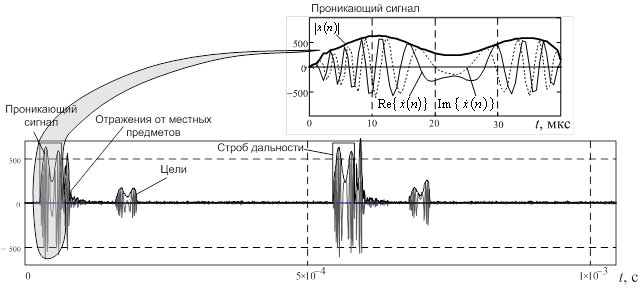
Рис. 3. Фрагменты записи сигналов РЛС, отраженных от двух самолетов Як-52,

сопровождаемых на дальности 24 км и азимуте 145º в режиме ЛЧМ

Предварительная цифровая обработка сигналов в режиме КНИ

Поскольку цель исследования заключалась в доказательстве принципиальной возможности сверхрэлеевского разрешения эхосигналов групповых воздушных объектов в реальных условиях, то интервалы наблюдения выбирались так, чтобы стандартные методы согласованной обработки сигналов (корреляционно-фильтровая обработка для КНИ и фильтровая для ЛЧМ) не обеспечивали бы разрешения объектов. При обработке сигналов с КНИ предварительно использовался интервал порядка 1,3 мс, содержащий пачку из 32 импульсов. Этот интервал времени не обеспечивал разрешения группового объекта стандартным методом дискретного преобразования Фурье (ДПФ) в ходе корреляционно-фильтровой обработки. Интервал наблюдения сигнала с ЛЧМ ограничивался его длительностью, т. е. обрабатывался одиночный радиоимпульс с ЛЧМ.

Для правильного измерения радиальной скорости объектов необходимо, чтобы модуляция комплексной огибающей сигналов адекватно воспроизводила колебания с частотами Доплера. Если обратиться еще раз к схеме РЛС (см. рис. 1), то можно заметить, что когерентный гетеродин при преобразовании сигнала с частоты -28 МГц на частоту навязывает свою фазу. Поскольку при приеме сигнал снимается тройником сразу после ПУПЧ, то фаза КГ, навязанная при преобразовании сигналов в передающей системе и изменяющаяся с частотой 28 МГц, сохраняется уже в цифровой записи на выходе АЦП (,– количество отсчетов записи). В приемной системе РЛС при преобразовании частоты вниз фаза колебаний КГ вычитается, никак не влияя на точность измерения частоты Доплера. В нашем случае для обеспечения правильного измерения частоты Доплера и вычитания фаз КГ в каждом периоде следует осуществлять свертку отраженного сигнала с зондирующим сигналом, проникающим в приемник. При обработке сигналов с ЛЧМ такая схема реализуема, так как при большом периоде следования сигнала с ЛЧМ отраженный сигнал будет находиться именно в этом периоде. Другая сложность заключается в том, что из-за разброса параметров аналоговой аппаратуры период следования импульсов не всегда одинаков, что требует сложных алгоритмов «вырезания» проникающего сигнала в каждом периоде следования записи .

При обработке сигналов КНИ схема свертки еще более усложняется, и кроме вышеописанных недостатков добавляется отсутствие информации о номере периода, в который попадает отраженный от объекта сигнал. Поэтому схема свертки с проникающим сигналом в режиме КНИ если и работает, то существенно усложнена в реализации.

Чтобы упростить обработку записей, не прибегая к существенному усложнению за счет использования каких-либо пороговых и морфологических алгоритмов выделения проникающего сигнала, была использована довольно простая схема цифрового гетеродинирования сигнала вниз с частотой 28 МГц. Сущность ее заключается в том, что все отсчеты записи умножаются на комплексную экспоненту с оценкой частоты когерентного гетеродина , в результате чего получали преобразованный сигнал вида

где– интервал дискретизации АЦП по времени.

Поскольку значение частоты КГ равной 28 МГц известно номинально, то для ее правильного измерения при обработке записей сигнала КНИ использовался следующий прием. С помощью стробов дальности длительностью в дискретных отсчетов (в нашем случае , ) выделялись отсчетов в пределах каждого из 32 импульсов пачки сигнала КНИ, в результате интегрирования которых формировалась выборка из () отсчетов (рис. 4), представляющих собой колебание с частотой (сумма колебаний частоты Доплера со смещением частоты КГ ):

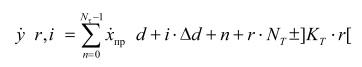где -28 МГц;

– смещение первого проникающего импульса от начала записи;

– номер строба дальности;

– смещение отраженного импульса от проникающего;

– количество отсчетов в периоде следования импульсов КНИ;

– коэффициент учета линейного увеличения или сжатия периода следования импульсов;

– символ округления до ближайшего целого числа.

Рис. 4. Временная реализация прореженного КНИ сигнала в первом стробе дальности

Выполнив ДПФ выборки с дополнением нулями вида

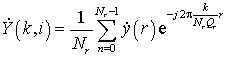были получены спектры сигналов из () отсчетов для каждого строба дальности, где скважность дополнения нулями выборки . Из всей совокупности спектров выбирался спектр строба дальности, имеющий максимальный ДПФ в области доплеровских частот объекта (рис. 5). В спектре сигнала нулевого строба дальности доминирующее положение занимает пик проникающего сигнала (см. рис. 4), хотя сигналы, отраженные от местных предметов имеют такую же частоту Доплера. При гетеродинировании с частотой (если она равна частоте КГ) пик проникающего сигнала и местных предметов находится строго в нуле. Для исследуемого фрагмента записи удалось установить частоту КГ равную 28,0065 МГц, откуда следует, что имело место смещение частоты КГ на 6,5 кГц вверх.

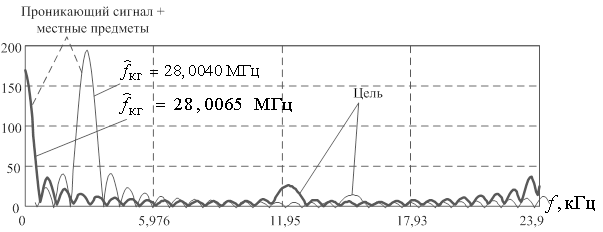
Рис. 5. ДПФ временной реализации прореженного КНИ сигнала первого

и нулевого стробов дальности при оценке частоты КГ 28,0065 МГц

Сформированная прореженная запись комплексного сигнала , представленного двумя квадратурами (см. рис. 4), использовалась далее для применения процедур обработки сигналов со сверхрэлеевским разрешением.

Предварительная цифровая обработка сигналов в режиме ЛЧМ

В режиме ЛЧМ обрабатывались одиночные радиоимпульсы с линейной частотной модуляцией. По аналогии с сигналом КНИ исходная запись умножалась на и формировалась запись , в которой проникающий сигнал должен был иметь спектр с шириной 900 кГц, определяемый девиацией. Записав проникающий сигнал в виде массива , где (для ЛЧМ ), выполним согласованную обработку сигналов с помощью операции

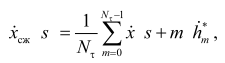
где , после чего, гетеродинируя сжатые сигналы, получим

Выполнив гетеродинирование проникающего сигнала, получим также

Если объект обнаружен (т. е. пик сжатого сигнала преобладает над шумами), то в окрестности пика сжатого импульса необходимо выделить 128 отсчетов (64 слева от пика включая пик и 64 справа) и выполнить над преобразованным сжатым сигналом операцию ДПФ

(1)

Если оценка частоты КГ верная, то аналогичная операция ДПФ над гетеродинированным проникающим сигналом даст спектр без разрыва (рис. 6), в котором составляющие, несущие энергию сигнала, распределены от нулевой частоты до частоты девиации 900 кГц. Если оценка частоты гетеродина ошибочная, то спектр получит разрыв. Зная девиацию частоты можно подобрать частоту гетеродина так, чтобы спектр гетеродинированного проникающего сигнала с ЛЧМ не имел разрыва (см. рис. 6).

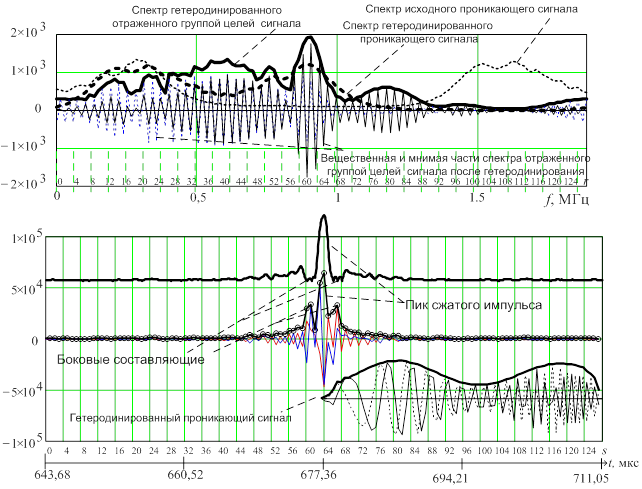
Рис. 6. Временные реализации и спектры ЛЧМ сигналов до и после гетеродинирования и сжатия

Оценка частоты гетеродина позволила после преобразования сжатых сигналов по частоте получить спектр отраженного сигнала с ЛЧМ, представляющий собой в частотной области сумму нескольких гармоник (см. вещественную и мнимую части на рис. 6). Поскольку частота дискретизации была вдвое больше девиации частоты 900 кГц, то в результате 128-и точечного ДПФ сжатого сигнала получен спектр, энергия которого сосредоточена в области первых 64 отсчетов (частот от 0 до 1000 кГц). Поэтому для обработки сигнала достаточно выбрать первые 64 отсчета ДПФ, несущие наиболее мощные гармоники спектра сигнала группового объекта.

Из рис. 6 видно, что амплитуда проникающего ЛЧМ радиоимпульса не постоянна на всей длительности, а именно уменьшается в области средних частот девиации, что связано с искажениями при формировании сигнала импульсным модулятором передатчика. Спектр сжатого проникающего сигнала (см. рис. 6) также имеет впадину в области средних частот. Это эквивалентно амплитудной модуляции спектра сигнала с ЛЧМ, что в конечном итоге выливается в два боковых всплеска сжатого импульса (см. рис. 6).

При решении задачи спектрального оценивания такая паразитная модуляция спектра приведет к искажениям и, как следствие, к невозможности сверхрэлеевского разрешения сигналов в частотной области. Поэтому прежде чем формировать спектр отраженного сигнала с ЛЧМ сначала необходимо подавить боковые всплески (гармоники спектра) сжатого импульса, после чего выполнять его перевод в область частот. На рис. 6 чуть выше сжатого импульса показано обратное ДПФ (ОДПФ) с дополнением нулями спектра сжатого импульса с подавленными боковыми составляющими.

Сверхрэлеевское разрешение объектов спектральными методами в импульсно-доплеровском режиме работы РЛС

В настоящей работе в рамках спектральных методов рассмотрены исходные [1, 2] и когерентные [3–5] методы линейного предсказания вперед-назад, эффективно решающие задачи сверхрелеевского разрешения, ограниченного шириной главного лепестка ДПФ выборки данных. Поэтому рассмотрим задачу линейного предсказания вперед-назад для исходного и когерентного подхода в общем виде применительно к экспериментальным выборкам сигналов, отраженных от группового объекта.

Рассмотрим выборку из дискретных отсчетов , полученных после децимации КНИ сигнала при обработке вышеописанным способом (см. рис. 4). Прежде чем формировать матрицу данных из отсчетов разобьем эту выборку на субвыборок из отсчетов (рис. 7).

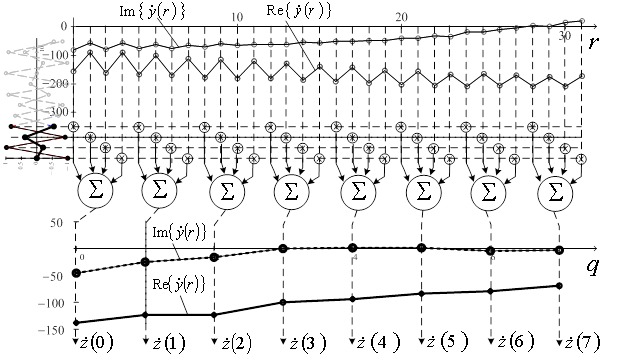
Рис. 7. Схема формирования вторичных отсчетов выборки

Просуммировав когерентно отсчеты каждой из субвыборок

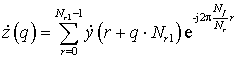, (2)

получим отсчеты вторичной (прореженной) выборки, где номер отсчета прореженной выборки; – резонансная частота фильтров первичной обработки (ФПО) с импульсной характеристикой , в которых обрабатываются отсчеты первичной выборки. Формирование отсчетов вторичной выборки эквивалентно обработке сигналов в системе ФПО с комплексными частотными характеристиками (КЧХ) вида

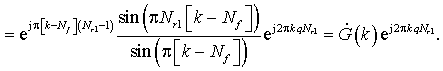
Из последнего выражения видно, что амплитудно-частотные характеристики фильтров одинаковые и определяются функцией «арочный синус», а фазо-частотные характеристики (ФЧХ) отличаются элементом задержки . Резонансная частота фильтров может выбираться в окрестности энергетического центра частот, определяемого операцией ДПФ отсчетов выборки .

Из отсчетов вторичной выборки составляется система уравнений вида

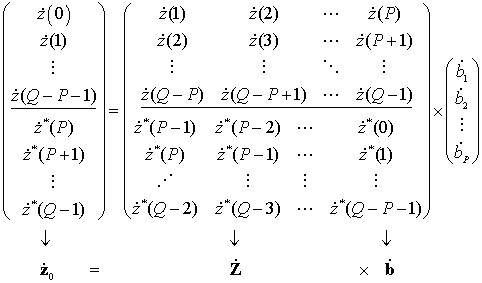(3)

откуда получим систему

определяющую корреляционную матрицу (КМ) и вектор весовых коэффициентов (ВВК) авторегресии , где – порядок модели авторегресии; – опорный вектор (ОВ) системы уравнений фазового метода с когерентным накоплением и прореживанием [5]. ВВК может быть также определен из эквивалентной системы вида

где

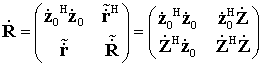(4)

В случае исходных методов авторегресии без применения каких-либо процедур когерентного накопления вторичная выборка не формируется и , откуда следует, что . Заменив в системе (3) на получим систему уравнений ВВК авторегресии для исходного метода, описанного в [1].

Спектральные функции методов линейного предсказания вперед-назад в общем виде будут иметь вид

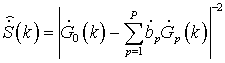, . (5)

Для отображения спектров относительно оси частот необходимо определить каждую частоту , где 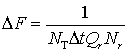– шаг отсчетов ДПФ по частоте. Оценивать частоты можно путем непосредственного анализа спектральных функций или корней характеристических полиномов фазовых методов из уравнения

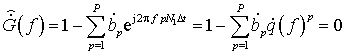(6)

и амплитудного метода

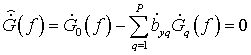. (7)

где – аргумент для фазового метода.

Вычислив оценки частот M источников, можно вычислить амплитуды источников путем решения обратной задачи. Для этого определяется матрица значений КЧХ каналов на этих частотах

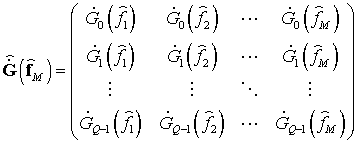и вектор 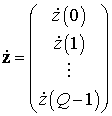(8)

откликов каналов на сигнал, связанные системой уравнений

, (9)

откуда найдем вектор комплексных амплитуд источников

. (10)

Для исходных методов спектрального анализа без прореживания данных величина аргумента характеристического полинома будет равна единице, а величина . Спектральные функции и корни характеристического полинома для исходного и когерентного методов спектрального анализа показаны на рисунках 8, 9.

Рис. 8. Спектральные функции когерентного (верху) с порядком модели 4

и исходного (внизу) с порядком модели 40 методов линейного предсказания вперед-назад

и оценки корней характеристического полинома и их амплитуд

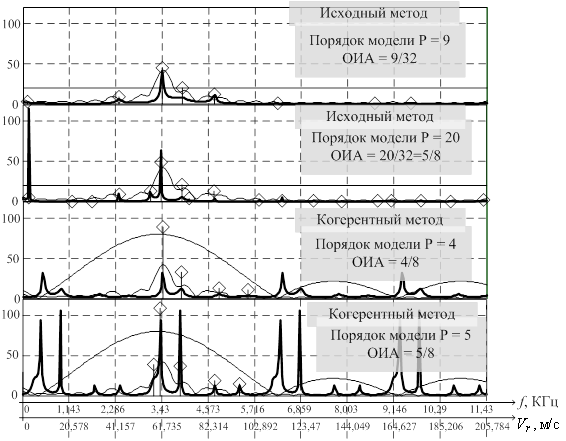
Рис. 9. Спектральные функции исходного (два верхних) и когерентного (два нижних)

методов линейного предсказания вперед-назад и оценки корней

характеристического полинома и их амплитуд

Из рис. 8 видно, что разрешающиеся по частоте Доплера объекты имеют радиальную скорость свыше 100 м/с, что достаточно много для самолета такого класса как Як-52. Взятие на сопровождение объекта осуществлялось, как правило, в режиме ЛЧМ, после чего РЛС переключалась в режим КНИ. Отсюда следует, что, при переключении в КНИ из ЛЧМ ракурс объектов был таковым, что их радиальная скорость составляла величину меньше 50 м/с и планерные составляющие были подавлены фильтром-преселектором приемника сопровождения КНИ. Из-за этого на сопровождении были взяты винтовые составляющие спектра эхосигнала и, групповой объект сопровождался по направлению. Для сравнения на рис. 9 показаны спектральные функции объекта, сопровождаемого в режиме КНИ на дальности около 9 км, причем ракурс был таковым, что планерные составляющие уверенно сопровождались РЛС, а по спектральной функции можно вычислить радиальную скорость объектов, которая составила около 60 м/с.

Сверхрэлеевское разрешение объектов спектральными методами в когерентно-доплеровском режиме работы РЛС

Для спектрального анализа сигналов по временной задержке аналогичными способами обрабатывается спектр сжатого ЛЧМ сигнала (см. рис. 6). В этом случае обрабатываются комплексные отсчеты ДПФ сжатого ЛЧМ импульса (рис. 10), как обрабатывалась временная реализация КНИ сигнала. При этом из 128 отсчетов спектра ЛЧМ импульса использовались первых отсчета, в которых заключалась большая часть энергии сигнала (см. рис. 10). Путем перемножения отсчетов спектра и частотной характеристики строба первичной обработки (СПО) с последующим суммирование формировались отсчеты вторичного спектра

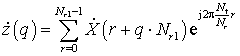, (11)

где – позиция СПО на временной шкале в дискретных отсчетах, в нашем случае .

Комплексные временные характеристики СПО по аналогии с характеристиками ФПО описываются функцией «арочный синус» во временной области

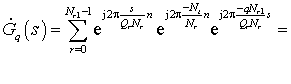
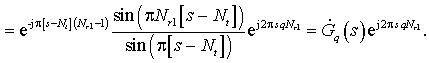
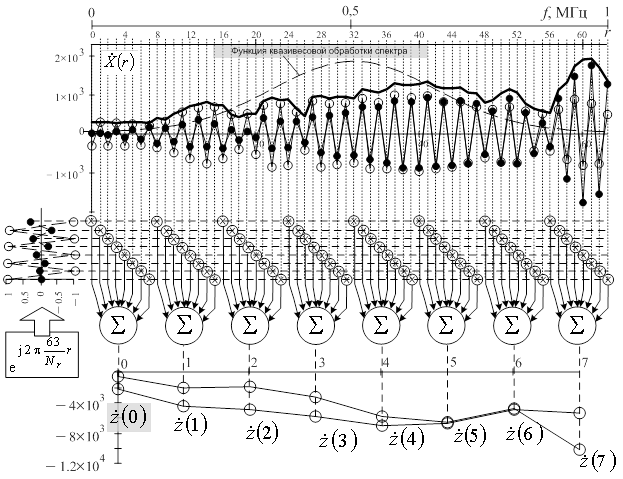
Рис. 10. Схема формирования вторичных спектральных отсчетов

ЛЧМ сигнала при когерентной обработке

С помощью отсчетов вторичного спектра , ,…, ЛЧМ сигнала формируется система уравнений (3), решением которой находим весовые коэффициенты линейного предсказания, так же как и в частотном случае. Используя формулы (5) – (10), меняя в них индексы на , переменные на и вектор на , получим спектральные функции и характеристический полином для описания временного (дальностного) портрета объектов и поиска корней характеристического полинома и их амплитуд, характеризующих амплитуды источников. В данном случае формируется спектральная функция в виде не функции от частоты, а функции от времени, т. е. функции описывающей распределение амплитуд рассеивающих центров на шкале временных задержек, соответствующих дальностям (рис. 11). На рис. 11 приведены временные спектральные функции, представляющие обратные по модулю функции взвешенной весовыми коэффициентами суммы комплексных СПО. Из рис. 11 видно, что спектральные функции содержат несколько раздельных пиков. Причем видно, что спектральные функции когерентного и исходного методов при одинаковом относительном интервале анализа дают равные по качеству спектральные оценки.

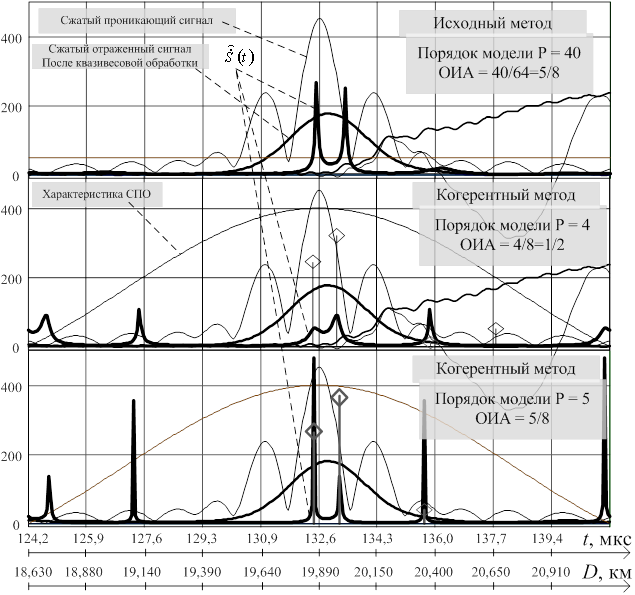
Рис. 11. Временные функции (дальностные портреты) группового объекта

(разность дальностей воздушных объектов составила 114 м)

Сверхрэлеевское разрешение объектов методами статистических решений в импульсно-доплеровском режиме работы РЛС

В настоящей работе экспериментально проверены наиболее эффективные модификации методов наименьших квадратов и максимального правдоподобия. Сущность этих методов и некоторые результаты оценки их эффективности путем математического моделирования рассмотрены в работах [18, 20].

На рис 12 представлен результат стандартной корреляционно-фильтровой обработки (КФО) цифровой записи 32-х периодов комплексной огибающей отраженного сигнала в импульсно-доплеровском режиме работы РЛС (см. рис. 2).

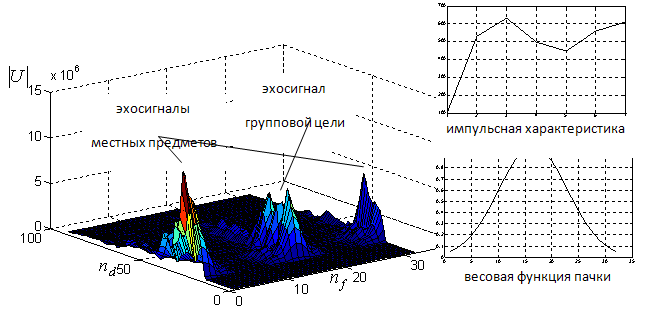
Рис. 12. Результат стандартной корреляционно-фильтровой обработки

отраженного сигнала в импульсно-доплеровском режиме работы РЛС

На рис. 12 по оси абсцисс отложено значение номера частотного фильтра , по оси ординат – номера строба дальности , а по оси аппликат – значение модуля накопленного сигнала в относительных единицах. На рис. 12 в центре наблюдается эхосигнал группового объекта, а на частотах Доплера с номерами частотных фильтров и эхосигналы местных предметов. Стандартная КФО на этапе внутрипериодной обработки была реализована путем свертки входного эхосигнала с импульсной характеристикой одиночного зондирующего сигнала (см. рис. 12) с шагом равным интервалу дискретизации АЦП мкс. Последняя формировалась как комплексно-сопряженная копия, проникающего на вход приемного тракта зондирующего сигнала (см. рис. 2). На этапе межпериодной обработки реализован алгоритм БПФ с интервалом когерентного накопления сигнала порядка 1,3 мс, содержащий пачку из 32 импульсов. При этом для снижения уровня боковых лепестков в частотной области проводилось взвешивание огибающей пачки во времени гауссовой функцией вида с эффективной шириной окна (см. рис. 12). Далее осуществлялось подавление эхосигналов местных предметов, для чего обнулялись амплитуды сигналов Доплеровских фильтров с номерами и . Последний результат обработки показан на рис. 13. Как следует из рис. 13 стандартная КФО не обеспечивает разрешения отдельных объектов из состава группового ни по времени запаздывания (дальности), ни по частоте Доплера (радиальной скорости).

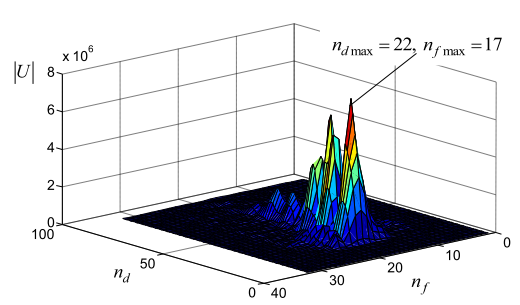
Рис. 13. Результат стандартной корреляционно-фильтровой обработки

после подавления эхосигналов местных предметов

Результаты разрешения сигналов во временной области представлены на рис. 14. На нем показаны нормированные графики входного эхосигнала группового объекта (штрих-пунктирная линия синего цвета), стандартной фильтровой обработки одиночного импульса (сплошная линия черного цвета) и оценки амплитуд эхосигналов отдельных объектов из состава группового после их разрешения по времени запаздывания (дальности) (сплошная линия красного цвета). Для реализации алгоритмов разрешения объектов использовалось сечение матрицы стандартной КФО вдоль оси ординат (стробов дальности ) для того номера частотного фильтра, в котором наблюдалась максимальная амплитуда сигнала (см. рис. 13). Из рис. 14 видно, что условия для разрешения объектов по времени запаздывания (дальности) весьма сложные, т. к. наблюдается достаточно много ложных пиков, не связанных с реальным количеством эхосигналов отдельных объектов, присутствующих в эхосигнале. Несмотря на это происходит правильное определение как количества отдельных объектов в составе группового, так и их времен запаздывания (дальностей). Конкретные оценочные показатели представлены на рис. 14.

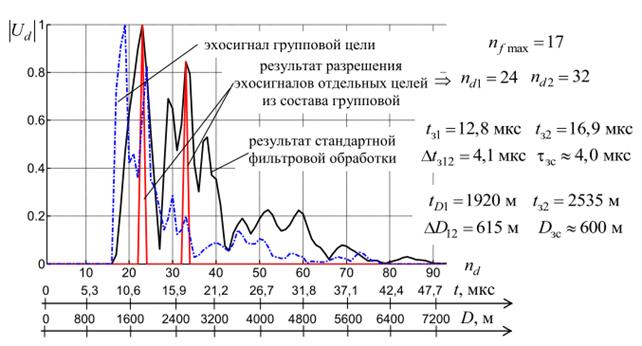
Рис. 14. Результаты разрешения сигналов во временной области

Результаты обработки эхосигналов в интересах их разрешения в частотной области представлены на рис. 15. На нем показаны нормированные графики результатов стандартной КФО эхосигнала группового воздушного объекта (линия черного цвета) и результат его разрешения в частотной области (линия красного цвета). Для реализации алгоритмов разрешения объектов использовалось сечение матрицы стандартной КФО вдоль оси абсцисс (номеров частотных фильтров ) для того номера строба дальности, в котором наблюдалась максимальная амплитуда сигнала (см. рис. 13). Из рис. 15 видно, что наблюдается уверенное разрешение отдельных объектов из состава группового в частотной области в пределах ширины доплеровского фильтра, т. е. определение их количества и частот (радиальных скоростей). Конкретные оценочные показатели представлены на рис. 15. На рис. 16 представлена результирующая амплитудно-частотная характеристика (АЧХ) одного канала БПФ в районе эхосигнала группового объекта после проведения стандартной КФО и взвешивания пачки импульсов гауссовой функцией (см. рис. 12) в интересах уменьшения боковых лепестков АЧХ. При этом учитывалось, что в результате весовой обработки ширина главного лепестка АЧХ доплеровского фильтра расширялась по сравнению с прямоугольной пачкой примерно в 1,6 раза и составила по частоте Доплера или по радиальной скорости.

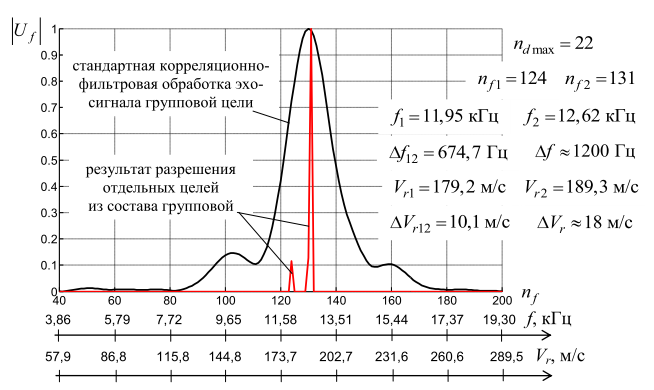
Рис. 15. Результаты разрешения сигналов в частотной области

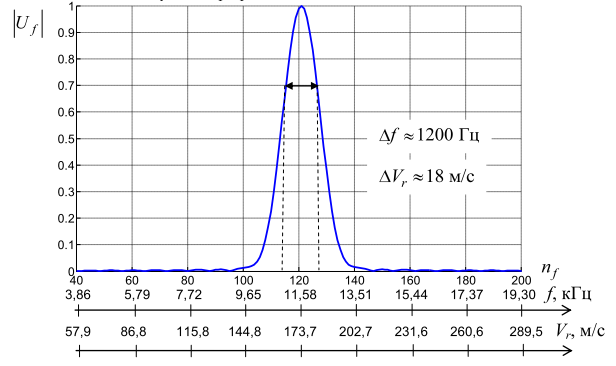
Рис. 16. Результирующая амплитудно-частотная характеристика фильтра

после стандартной КФО и взвешивания гауссовым окном

Заключение

Результаты обработки эхосигналов КНИ и с ЛЧМ реальной РЛС в когерентно-импульсном и импульсно-доплеровском режимах работы, сопровождавшей групповой воздушный объект, свидетельствуют о принципиальной возможности практического применения алгоритмов сверхрэлеевского разрешения по дальности и скорости методами цифрового спектрального анализа и некоторыми модификациями методов максимального правдоподобия и наименьших квадратов в условиях искажений временной и частотной структуры сигналов в приемо-передающих трактах РЛС.

Для эффективного практического применения методов сверхрэлеевского разрешения во временной и частотной областях необходимо, чтобы зондирующий сигнал обеспечивал спектральную для сверхрэлеевского разрешения по частоте и временную для сверхрэлеевского разрешения по дальности «чистоту». Другими словами, в спектре зондирующего сигнала не должны присутствовать составляющие, обусловленные амплитудной, частотной или фазовой модуляцией вследствие нестабильной работы передающего тракта РЛС. Во временной области сигнал должен обладать высоким коэффициентом прямоугольности и центральной симметрии, которые необходимо сохранять при прохождении сигнала через весь приемо-передающий тракт РЛС. Кроме того, необходимо учитывать известную и поддающуюся аналитическим оценкам трансформацию сигнала в ходе стандартной корреляционной (фильтровой или корреляционно-фильтровой) обработок. Например, к такой трансформации можно отнести весовую обработку сигналов во временной области с целью уменьшения уровня боковых лепестков амплитудно-частотных характеристик доплеровских фильтров, приводящая к существенном изменению их формы. При существующем уровне развития методов цифрового формирования и обработки сигналов, обеспечение требуемой «чистоты» сигналов во временной и частотной областях вполне возможно. Например, это может быть реализовано на базе цифровых синтезаторов частоты и микросхем программируемой логики.

Альтернативным выходом может быть обработка с формированием копий эталонных корреляционных функций эхосигналов одиночных объектов во временной и частотной областях из проникающего в приемный тракт зондирующего сигнала с последующей коррекцией искажений так, как это было осуществлено с экспериментальными данными, представленными в настоящей статье. Однако такой подход в интересах реализации высокой эффективности методов сверхрэлеевского разрешения является менее продуктивным.

Литература

1. Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения / Пер. с англ. М.: Мир, 1990.

2. Stoica P, Moses R. L. Introduction to Spectral Analysis. New Jersey, Prentice-Hall, Inc. 1997, 319 p.

3. Савинов Ю. И. Когерентный метод Прони с квазипрореживанием//Вопросы радиоэлектроники. Серия РЛТ. Вып. 3, 2008. С. 122–128.

4. Абраменков В. В. Измерение угловых координат М источников излучения методом нормирования сигнала к амплитудам образовавших его источников//Сб. статей. Авионика 2002 – 2004. М.: Радиотехника, 2005. С. 218 – 221.

5. Григорян Д. С. Сверхразрешение по частоте при обработке радиолокационных сигналов когерентными методами линейного предсказания вперед-назад с прореживанием данных – "Журнал радиоэлектроники (электронный журнал)". №7, 2011. http://jre.cplire.ru

6. Григорян Д. С., Семченков С. М. Сверхразрешение по дальности при обработке радиолокационных сигналов с линейной частотной модуляцией когерентным методом линейного предсказания вперед-назад с прореживанием данных – "Журнал радиоэлектроники (электронный журнал)". №8, 2011. http://jre.cplire.ru/

7. Ширман Я. Д. Разрешение и сжатие сигналов. - М.: Сов. радио, 1974. - 315 с.

8. Шинаков Ю. С., Сперанский В. С. Совместное обнаружение, разрешение и измерение параметров сигналов на фоне помех на выходе антенной решетки. Синтез алгоритма//Радиотехника и электроника. - 1982. - Т. 27. - №11. - С. 2179-2184.

9. Варюхин В. А., Покровский В. И., Сахно В. Ф. Модифицированная функция правдоподобия в задаче определения угловых координат источников с помощью антенной решетки//ДАН СССР. - 1983. - Т. 270. - №5. - С. 1092-1094.

10. Курикша А. А. Оценка числа и параметров компонент сигнала при наличии шума//Радиотехника и электроника. - 1984. - Т. 29. - №9. - С. 1740-1744.

11. Шинаков Ю. С. Совместное обнаружение и разрешение неизвестного числа сигналов//Радиотехника и электроника. - 1985. - Т. 30. - №6. - С. 1131-1138.

12. Коновалов Л. Н. Определение числа сигналов методом проверки сложных гипотез по критерию отношения правдоподобия//Радиоэлектроника. - 1988. - Т. 31. - №7. - С. 18-24.

13. Сычев М. И. Оценивание числа близко расположенных источников по пространственно-временной выборке//Радиотехника и электроника. - 1992. - Т. 37. - №10. - С. 1807-1814.

14. Варюхин В. А. Основы теории многоканального анализа. – Киев, ВА ПВО СВ им. А. М. Василевского. 1993.

15. Журавлев А. К. Определение числа и координат точечных источников излучения, не разрешаемых по критерию Рэлея//Радиотехника. - 1995. - №2. - С. 62-66.

16. Слюсар В. И. Синтез алгоритмов измерения дальности М источников при дополнительном стробировании отсчетов АЦП//Радиоэлектроника. - 1996. - №5. - С. 55-62.

17. Аганин А. Г. Разрешение сигналов по доплеровской частоте на основе проверки статистических гипотез//Радиотехника. - 2001. - №1. - С. 24-29.

18. Абраменков В. В., Климов С. А., Савинов Ю. И. Способ и устройство измерения дальностей до М источников вторичного излучения, сигналы которых перекрываются во времени//Радиотехника. - 2002. - №1 - С. 32-38.

19. Акимцев В. В., Гниденко И. Ю. Алгоритм разрешения-обнаружения целей по дальности в обзорных РЛС//Радиотехника. - 2002. - №1 - С. 61-66.

20. Чижов А. А. Метод разрешения групповых сосредоточенных целей//Радиотехника. - 2009. - №10 - С. 4-12.

21. Митрофанов Д. Г. Исследование отражательных характеристик воздушных объектов в условиях проявления траекторных нестабильностей//Известия института инженерной физики. 2009. № 3, т. 9. С. 37–46.