УДК 621.371+537.87

МИКРОВОЛНОВАЯ ПОДПОВЕРХНОСТНАЯ ГОЛОГРАФИЯ СПЛОШНЫХ ДИЭЛЕКТРИЧЕСКИХ ОБЪЕКТОВ

К. П. Гайкович¹, Е. С. Максимович², В. А. Бадеев²
 

¹ Институт физики микроструктур Российской академии наук, г. Нижний Новгород

 ² Институт прикладной физики Национальной академии наук Беларуси, г. Минск

Получена 25 мая 2012 г. 
 

Аннотация. Предложен метод компьютерной сканирующей голографии (восстановления формы поверхности) подповерхностных диэлектрических объектов, основанный на решении соответствующей обратной задачи ближнепольного рассеяния по данным многочастотных измерений двумерного распределения рассеянного поля у  поверхности среды над областью неоднородностей. Метод апробирован по данным измерений тестовых образцов в грунте.

Ключевые слова: голография, диэлектрик, неоднородные среды, рассеяние СВЧ излучения.

Summary. A method of the scanning computer holography (retrieval of the surface shape) of subsurface dielectric objects, based on the solution of the near-field inverse scattering problem by data of 2D multifrequency measurements of scattered field near the medium surface above sounded inhomogeneities, is proposed. This method has been verified by data of measurements of test samples buried in the ground.

Key words: holography, dielectric, inhomogeneous media, scattering of microwave radiation.

 

Введение

Голография как способ записи и воспроизведения отраженной от объекта волны был предложен Д. Габором [1], а потом для его реализации было предложено использовать лазеры [2]. Как известно, в классической голографии и радиоголографии (см. в [3-6]) используется аналоговый метод записи на регистрирующих средах комплексных амплитуд интерференционной картины поля, создаваемой опорной и отраженной от объекта (объектной или предметной) волнами (радиоголограмма), с последующей реконструкцией и визуализацией в оптическом диапазоне поля, подобного отраженной волне. В дальнейшем стали применяться численные методы реконструкции [7-9], а область применения методов существенно расширилась, включив и акустическую голографию [9-11]. Методы радиоголографии нашли применение в системах радиовидения, для дистанционного зондирования земной поверхности, атмосферы и ионосферы из космоса, в том числе, с использованием GPS, в радиоастрономии, для определения характеристик больших антенн.

Начались исследования возможностей радиоголографии в СВЧ диапазоне для зондирования подповерхностных объектов. Первые результаты показали новые возможности использования метода в дефектоскопии [12-14]. Так, в последней из этих работ для восстановления двумерной функции, характеризующей рассеяния от плоских, параллельных поверхности среды объектов предлагается использовать результаты измерений рассеянного сигнала методом двумерного сканирования в моностатической конфигурации. Изображение получается из численного решения двумерного интегрального уравнения типа свертки, предложенного авторами для описания принимаемого сигнала.

В отличие от упомянутых работ [12-14], где исследовались возможности визуализации сильно рассеивающих (металлических) неоднородностей, в данной статье рассматривается восстановление формы относительно слабоконтрастных диэлектрических объектов на основе решения трехмерной обратной задачи рассеяния. При этом для неоднородностей, зондируемых в ближней зоне, оказывается возможным достигнуть высокой (субволновой) разрешающей способности. Реализация этой цели позволила бы восстанавливать форму всей поверхности внутренне однородных объектов. Постановка такой задачи базируется на наших результатах в решении обратных задач ближнепольного рассеяния и предложенных на их основе методов сканирующей подповерхностной томографии, в частности многочастотного метода [15,16].

По существу, такой подход основан на принципе, используемом в сканирующей ближнепольной оптической микроскопии для получения двумерных изображений поверхности с субволновым разрешением, который обобщается здесь на трехмерные задачи томографии и голографии. Поле излучения локализованного источника может быть представлено поперечным спектром плоских волн, который содержит и затухающие ближнепольные компоненты, за счет чего можно реализовать субволновую разрешающую способность. В многочастотном методе изменение эффективной глубины зондирования достигается путем трансформации размеров ближней зоны поля при перестройке частоты зондирующего сигнала. Использование специфики ближнепольных измерений для достижения необходимой разрешающей способности становится единственно возможным методом, когда применение для этой цели более коротких длин волн затруднено из-за их сильного поглощения или рассеяния в среде.

Рассматриваемый здесь подход реализует метод сканирующей электромагнитной томографии [15], основанный на сведении обратной задачи рассеяния к решению трехмерного нелинейного интегрального уравнения 1-го рода. Известно, что для таких задач неизбежны ограничения размерности сетки, на которой ищется решение и, как следствие, разрешающей способности. Эти трудности удалось в значительной мере преодолеть в [16] путем сведения этого уравнения к виду двумерной свертки по поперечным координатам, и, далее, к одномерному интегральному уравнению для глубинного профиля поперечного спектра неоднородностей комплексной диэлектрической проницаемости для каждой пары волновых чисел (в k-пространстве), причем для весьма общего случая неоднородности в многослойной поглощающей среде. Такая трансформация оказалась возможной при условии сохранения взаимного положения излучающего и принимающего зондов (сканировании жестко связанной системой источник-приемник). Ядро решаемого уравнения было получено в явном виде методом входных импедансов путем разложения определяющих его функций Грина в спектр плоских волн в k-пространстве. Соответствующая обратная задача, как и многие задачи дистанционного зондирования [17], в борновском приближении сводится к решению интегрального уравнения Фредгольма 1-го рода. Для решения этой некорректной задачи на классе комплекснозначных функция в [16] был разработан и исследован в численном моделировании алгоритм, основанный на принципе обобщенной невязки Тихонова. Обратное двумерное Фурье преобразование решения этого уравнения даёт искомую трёхмерную структуру неоднородности. Описанный подход допускает и некоторую коррекцию за пределами борновского приближения в рамках решения одномерного уравнения [16].

Первые результаты экспериментального исследования данного метода томографии были представлены в [18, 19]. Однако, в этих работах было установлено, что влияние поверхностного рассеяния так сильно зашумляет вклад зондируемых подповерхностных объектов в измеряемый сигнал, что оказывается невозможным получить качественное решение задачи. В [20] был предложен метод, позволяющий преодолеть эту трудность путем трансформации частотной зависимости решаемого уравнения во временную область, что позволяет разделить в полученном комплексном синтезированном импульсе (мы будем называть его для краткости псевдоимпульсом) вклад поверхностного и подповерхностного рассеяния и, тем самым, качественно улучшить чувствительность измерений к полю, рассеиваемому зондируемыми подповерхностными неоднородностями. Соответствующая трансформация решаемого интегрального уравнения приводит к новой постановке обратной задачи рассеяния и радикальному улучшению результатов использования ее решения для микроволновой томографии неоднородностей.

Поскольку в большинстве случаев подповерхностные неоднородности имеют однородную внутреннюю структуру, в данной работе предлагается метод восстановления из решения обратной задачи рассеяния формы таких объектов, т.е. метод компьютерной голографии.

 

Теория

Пусть имеется рассеивающая трехмерная неоднородность комплексной диэлектрической проницаемости  в среде с  (среда может быть многослойной), т.е. . Электромагнитное поле (комплексные амплитуды) может быть на частоте  представлено как сумма зондирующего и рассеянного полей . Для предлагаемой схемы измерений (см. на рис.1) с фиксированным вектором , определяющим сдвиг между приемной и передающей антеннами, поперечный спектр рассеянного поля (двумерное фурье-преобразования по x и y) в борновском приближении может быть представлен как интеграл от глубинного профиля поперечного спектра неоднородностей в виде [16]:

 

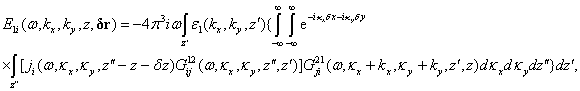        (1)

 

где- компоненты соответствующих функций Грина в k-пространстве,  - спектр распределения излучающего тока источника.

 

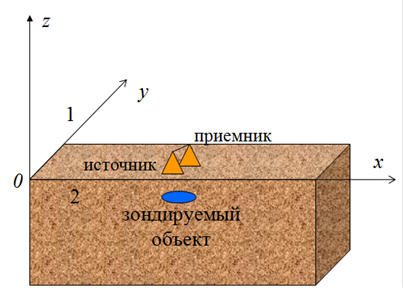
Рис.1. Схема измерений.

 

В случае измерений над средой с плоскослоистой основной структурой вариации принимаемого сигнала s, связанные с рассеянным на подповерхностной неоднородности полем, определяются сверткой по поперечным координатам передаточной функции приемника F и рассеянного поля .

                    ,                              (2)

 

где положение приемника определяется вектором . Это позволяет получить одномерное интегральное уравнение, связывающее поперечный спектр вариаций сигнала с глубинным профилем поперечного спектра неоднородностей диэлектрической проницаемости:

 

                       .                               (3)

 

Интегральное уравнение Фредгольма 1-го рода (3) должно решаться для каждой пары спектральных компонент. Для искомых функций в комплексном гильбертовом пространстве  был разработан регуляризирующий алгоритм решения [16], основанный на принципе обобщенной невязки Тихонова. Искомое трехмерное распределение (результат томографии) получается путем двумерного обратного фурье-преобразования полученного спектра. Исходными данными для анализа является двумерное распределение вариаций сигнала у поверхности среды над неоднородностью, измеренное на ряде частот. В [16] было показано, что в рамках решения уравнения типа (3) возможна и коррекция за пределами борновского приближения, для которой нужно внести соответствующие поправки в левую часть (3) или использовать для калибровки тестовые образцы со сравнимыми диэлектрическими параметрами.

Зависимость масштаба затухания сигнала в среде от частоты определяет глубинную чувствительность метода. Этот масштаб определяется как ближнепольными компонентами поперечного спектра рассеянного поля, так и поглощением в среде. При решении задачи с учетом ближнего поля не видно теоретических ограничений на разрешающую способность метода, однако, учитывая экспоненциальное затухание ближнепольных компонент и ненулевую погрешность измерений, такие ограничения неизбежно существуют, и разрешающая способность за пределами ближней зоны быстро стремится к релеевскому пределу.    

Решение уравнения (3) было использовано в наших первых исследованиях метода томографии по экспериментальным данным [18, 19]. Результаты показали, что наиболее серьезной проблемой метода являлся высокий уровень зашумленности данных поверхностным рассеянием, причем даже при весьма ровной поверхности над объектом, причем даже мелкомасштабные неоднородности вблизи антенны при многократном рассеянии порождают и крупномасштабные вариации принимаемого сигнала. Вместе с тем, нами экспериментально было установлено [20], что при трансформации многочастотных данных во временную область можно разделить вклад поверхностного рассеяния от рассеяния на зондируемом объекте в  эквивалентном псевдоимпульсе:

 

                            .                                    (4)

 

Такой импульс характеризует относительный вклад рассеяния с разных уровней глубины в соответствии со временем задержки, которому можно сопоставить эффективную глубину z_s:

 

                           .                                       (5)

 

Оказывается, что это преобразование позволяет получить отчетливое изображение рассеивающих объектов в грунте. Поэтому представлялось оправданным выполнить аналогичную (4) трансформацию частотных зависимостей в интегральном уравнении (3) к соответствующим временным распределениям; тогда (3) трансформируется в уравнение, в котором поперечные спектры зависят от параметра эффективной глубины формирования:

         

                                 .                             (6)

 

Такой подход был нами реализован в [20]. Полученное уравнение имеет серьезные преимущества по сравнению с (3). Появляется возможность обоснованно выбрать значения параметра z_s так, чтобы они перекрывали интервал, на котором имеется вклад зондируемого объекта – вне зоны влияния поверхности. Кроме того, можно существенно сузить область локализации объекта, в которой ищется решение. Проблема применения развитой теории на практике заключается в определении ядер в уравнениях (3), (6), поскольку не для всех антенн можно определить их вид теоретически. В [20] для этой цели было предложено использовать калибровку ядра уравнения по измерениям тестовых образцов в форме тонких параллелепипедов с известным поперечным спектром и продемонстрирована принципиальная осуществимость метода ближнепольной томографии (восстановления трехмерных распределений комплексной диэлектрической проницаемости) на основе решения (6) – как для распределенных, так  и для  сплошных (внутренне однородных) тестовых объектов.

Однако, поскольку на практике чаще всего приходится иметь дело со сплошными объектами, больший интерес представляет задача определения их формы, т.е. задача компьютерной голографии. Для этого необходимо ввести в алгоритм решения задачи дополнительную априорную информацию о постоянстве диэлектрических параметров внутри неоднородной области. Из общих соображений ясно, что такое сильное ограничение способно привести к существенно более точному решению задачи. Предлагаемый метод голографии основан на непосредственном использовании восстановленного из решения (6) распределения в предположении, что оно получено для объекта с известной постоянной внутренней комплексной диэлектрической проницаемостью.

Для этой цели зададим форму поверхности объекта в декартовой системе координат (рис.1) в виде  (см. на рис.2). При некотором значении сечение описывается двумя функциями:  – левее пунктирной линии и  – правее этой линии.

 

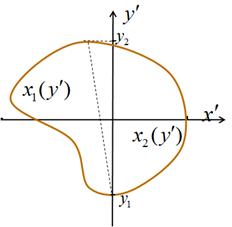
Рис.2. Граница сечения объекта при

 

Тогда для одномерного обратного фурье-преобразования этого спектра по k_y имеем комплексное уравнение:

 

                ,                       (7)

 

решение которого для двух неизвестных x₁ и x₂ задает искомую форму поверхности объекта. Поскольку решение может быть получено при каждом значении k_x, уравнение (7) является переопределенным, и, следовательно, имеется возможность его оптимизации.

Эксперимент

Метод исследовался на тестовых сплошных известной формы. Измерения выполнялись с помощью приемно-передающей сканирующей системы, состоящей из двух идентичных жестко связанных дипольных антенн, разнесенных на 4 см, и векторного анализатора Agilent E5071B, который позволял излучать зондирующий сигнал на 801 частоте в диапазоне 1,7 – 7 ГГц и измерять комплексные амплитуды рассеянного на неоднородностях  поля. Размеры области сканирования над поверхностью песчаного грунта составляли L_x = 30 см; L_y = 20 см. На рис.3a представлен измеренный спектр сигнала в средней точке области сканирования над объектом (пенопластовый образец размером 4×3×2 см на глубине z = –4 см), а на рис.3b соответствующее распределение псевдоимпульса в этой же точке.

 

Рис.3. (а) Спектр сигнала, измеренный в точке над объектом,; (b) амплитуда псевдоимпульса в зависимости от параметра эффективной глубины в той же точке.

 

На рис.3b можно видеть, что при z_s > –1,5 см на формирование псевдоимпульса оказывает сильное влияние поверхность зондируемой среды, тогда как в области, расположенной при  z_s < –1,5 см отчетливо видно распределение, связанное с подповерхностным объектом. Это позволяет при решении задач томографии и голографии использовать в анализе именно эту информативную область. На рис.4 представлены распределения псевдоимпульса по области сканирования для нескольких значений эффективной глубины.

 

Рис.4. Двумерные распределения псевдоимпульса при значениях параметра эффективной глубины z_s = –1,0, –4,8, –6,4, and –9,6 см.

 

Видно, что распределение псевдоимпульса на рис.4 при z_s = –1,0 см сформировано поверхностными неоднородностями, и на нем невозможно различить зондируемый объект. Однако в распределениях псевдоимпульса при z_s = –4,8 см и  z_s = –6,4 см можно отчетливо различить контуры зондируемого тестового объекта, что создает хорошие предпосылки для решения поставленной задач томографии и голографии из уравнений (6), (7). При z_s = –9,6 см контуры объекта расплываются. Заметим, что такие изображения могут быть использованы и непосредственно, без решения обратной задачи, для обнаружения и качественной диагностики подповерхностных объектов. Спектральный диапазон измерений для объектов сантиметрового масштаба со стороны высоких частот ограничен поглощением в среде, а со стороны низких – уменьшением рассеяния (рис.3a), так что хорошее разрешение объекта на рис.4 связано с ближнепольными компонентами рассеянного сигнала.

Распределения комплексного псевдоимпульса для 50 его значений в информативном диапазоне, полученные по данным измерений, были использованы для последующего анализа на основе (6) и (7). Решения уравнения (6)  было использовано при решении задачи голографии на основе уравнения (7).  

 

Рис.5. Голографическое изображение формы зондируемого объекта.

 

На рис. 5 можно видеть голографическое изображение формы зондируемого объекта, которая описывается двумя функциями, полученными из решения (7):  –  слева и  – справа. Хорошее соответствие с реальными геометрическими параметрами тестового образца показывает, что эти результаты являются весьма обнадеживающими. Но, разумеется, для того, чтобы довести предлагаемый метод до применения в практических приложениях, необходимо выполнить очень большой объем как теоретических, так и экспериментальных исследований.

 

Результаты получены при поддержке проекта совместных российско-белорусских исследований РФФИ-БРФФИ (№№ 12-02-90028_Бел-а, Т12Р-133 соответственно) и программы ОФН РАН.

 

Литература

1.     Gabor D. A new microsopic principle. Nature, 1948, v.161, pp. 777-778.

2.     Leith E. N., Upatnieks J. Reconstructed wave fronts and communication theory. J. Opt. Soc. America, 1962, v.52, No.4, XIV Advertisment.

3.     Р. Кольер, К. Бэркхарт, Л. Лин. Оптическая голография, изд. "Мир", М., 1975.

4.     Г. С. Сафронов, А. П. Сафронова. Введение в радиоголографию, изд. Сов. радио, М., 1973.

5.     Бахрах Л. Д., Гаврилов Г. А. Голография, М., Знание, 1979.

6.     Радиоголография и оптическая обработка информации в микроволновой технике. (Сб. Ст), под ред. Л. Д. Бахраха, А. П. Курочкина. Л., 1980.

7.     Балтийский С. А., Гуров И. П., Де Никола С., Коппола Д., Ферраро П. Современные методы цифровой голографии. В кн.: Проблемы когерентной и нелинейной оптики /Под ред. И.П. Гурова и С.А. Козлова. СПб: СПбГУ ИТМО, 2004. с. 91-117.

8.     Soutekh M. Fourier Array Imaging. Englewood Cliffs, Prentice-Hall, 1994.

9.     Воронин Е. Н., Воронин И. Н. Радио- и акустическая избирательная голография. М., МАКС Пресс, 2006.

10.    Гик Л. Д. Акустическая голография. М., Наука, 1981.

11.    J. D. Maynard, E. G. Williams, and Y. Lee. Nearfield Acoustic Holography: Theory of Generalized Holography and the Development of NAH, J. Acoust. Soc. Am., v. 78, No.4, pp. 1395-1413, 1985.

12.    Razevig V. V., Ivashov S. I., Sheyko A. P., Vasiliev I. A., Zhuravlev A. V. An example of holographic radar using at restoration works of historical building. Progress in Electromagnetic Research Letters. 2008, v.1, pp 173-179.

13.    Разевиг В. В., Васильев И. А., Журавлев А. В. Ивашов С. И. Разработка технологии голографических подповерхностных радиолокаторов и ее применение. Успехи современной радиоэлектроники. 2009, № 1-2, с.5-18.

14.    Разевиг В. В., Бугаев А. С., Ивашов С. И., Васильев И. А., Журавлев А. В. Восстановление микроволновых голограмм, полученных подповерхностным радиолокатором РАСКАН. Успехи современной радиоэлектроники. 2010, № 9, с. 51-58.

15.    Gaikovich K. P. Subsurface Near-Field Scanning Tomography. Physical Review Letters. 2007, vol. 98, p. 183902 (4 pp.).

16.    Gaikovich K. P., Gaikovich P. K. Inverse problem of near-field scattering in multilayer media. Inverse Problems.  2010, v.26, No. 12, p. 125013 (17 pp.).

17.    Gaikovich K. P. Inverse Problems in Physical Diagnostics. Nova Science Publishers Inc., New York, 2004.

18.    Gaikovich K. P., Gaikovich P. K., Maksimovitch Ye. S., Badeev V. A., Mikhnev V.A. Near-field microwave tomography. Proceedings of 7^th International Conference on Antenna Theory and Technique (6-9 October, 2009 Lviv, Ukraine), p. 262-264.

19.    Gaikovich K. P. , Gaikovich P. K., Maksimovitch Ye. S., Badeev V. A. Multifrequency microwave tomography of absorbing inhomogeneities. Proceedings of 5^th Int. Conf. “Ultrawideband and Ultrashort Impulse Signals” (6-10 September, 2010, Sevastopol, Ukraine) , p. 156-158.

20.    Гайкович К. П., Максимович Е. С., Бадеев В. А. Микроволновая сканирующая томография слабоконтрастных подповерхностных объектов. Сборник трудов XXVII Всероссийского симпозиума «Радиолокационного исследования природных сред» (17-19 мая 2011 г., Санкт- Петербург).