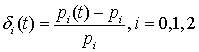Оценка качества обслуживания пакетной радиосети в нестационарном режиме в условиях воздействия внешних дестабилизирующих факторов

УДК 623.624

С. И. Макаренко

Военно-космическая академия имени А. Ф. Можайского

Получена 9 июня 2012 г.

Аннотация. Рассмотрен способ подавления пакетной радиосети, основанный на переводе сети в нестационарный режим функционирования, за счет периодического воздействия преднамеренных помех. Рассмотрены различные варианты воздействия в интересах снижения интенсивности обслуживания пакетов каналом множественного доступа. Обоснованы квазиоптимальные параметры воздействия в интересах эффективного подавления радиосети.

Ключевые слова: радиоэлектронное подавление, радиосеть, система массового обслуживания, нестационарный режим.

Abstract. We consider the method of repression of radio network with package transmitting based on the switching it to unstationary mode by means of periodical premeditated interferences influence. Different variants of premeditated interferences for decreasing of quality of service in multiple access channel are considered. Quasi-optimal parameters of the influence for the purpose of effective radio network repression are justified.

Keywords: the radio electronic countermeasures, the electronic warfare, the radio networks, queueing system, unstationary mode.

Обоснование новых возможностей подавления пакетной радиосети за счет изменения ее параметров и перевода в нестационарный режим функционирования

Данная статья продолжает цикл исследований автора в интересах решения проблемы подавления сетей связи за счет использования эффектов воздействия преднамеренных помех (ПП). Предлагается новый подход [1] который предполагает подавление сети связи за счет снижения качества обслуживания (QoS – Quality of service) систем связи (СС) на верхних уровнях модели взаимодействия открытых систем (OSI – Open system interconnect). Предлагаемый подход существенно отличается от сложившейся в настоящее время парадигмы применения средств радиоэлектронного подавления (РЭП) и постановки ПП, которые используются для подавления связи на физическом уровне модели OSI. Анализ работ, посвященных исследованию вопросов воздействия ПП на системы связи [2-6], а также вопросов развития и строительства сетей связи следующего поколения (NGN – Next generation net) [7] показывает, что современные системы связи, в том числе и специального назначения [8, 9], будут строиться на основе гетерогенных сетей, образованных различными средствами связи (космического, воздушного, полевого и наземного базирования). Вместе с тем существующая методология подавления СС и способы и формы применения средств РЭП против таких сетей не могут решить задачи подавления связи с заданным качеством.

В более ранней работе автора [10] отмечается, что одним из перспективных направлений применения РЭП является разработка способов подавления, основанных на внутренних особенностях функционирования системы связи. Так в исследовании [10] рассматривались возможности по переводу пакетной радиосети (ПРС) с временным разделением абонентов в нестабильное состояние работы путем воздействия ПП. Вместе с тем, общие возможности по применению принципа подавления функционирования СРС за счет искусственного перевода их в нестабильные и нестационарные режимы функционирования гораздо шире рассмотренных в работе [10]. Их общее отличие от существующих принципов подавления [2-6] состоит в том, что подавление СС в них происходит на канальном уровне модели OSI за счет учета особенностей функционирования абонентов в сети радиосвязи (СРС) и особенностей передачи информационных потоков.

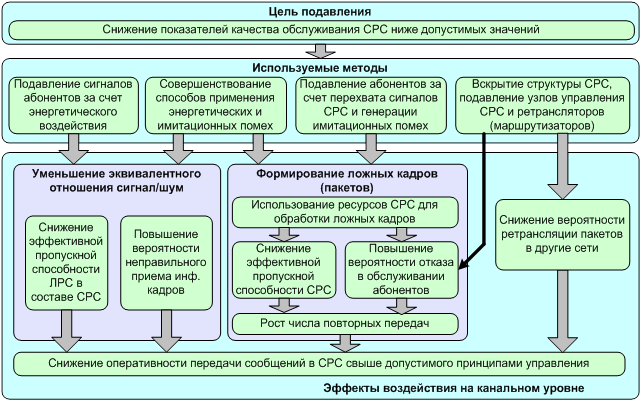
Рис. 1. Существующие подходы к подавлению СРС на канальном уровне OSI

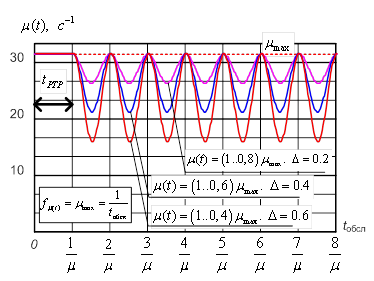
На рис. 1 представлены общие существующие подходы к подавлению СРС на канальном уровне модели OSI. Целью подавления является формирование таких условий функционирования СРС, в которых передача пакетов невозможна или существенна затруднена. В рамках данной статьи рассматривается задача изменения качества обслуживания СРС в интересах снижения ее пропускной способности. Для анализа путей решения поставленной задачи СРС была представлена в виде системы массового обслуживания (СМО) - рис. 3. Анализ данной модели показал, что варьируемыми параметрами СМО, которые могут быть использованы для перевода ее в режим функционирования с низким качеством, могут быть интенсивность входного трафика и интенсивность обслуживания разделяемого ресурса связи. В соответствии с этим может быть предложено две стратегии подавления СРС, представленные на рис. 2.

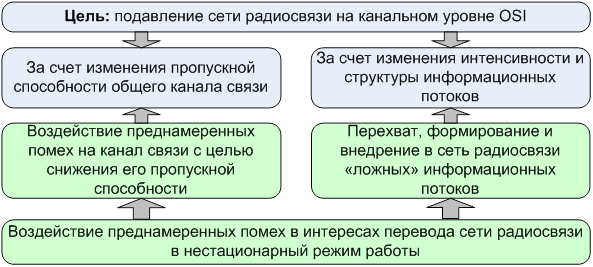
Рис. 2. Стратегии подавления СРС в интересах перевода ее в нестационарный режим функционирования

В статье рассматривается первый случай (рис. 2) - перевод СРС (представленной моделью СМО) в нестационарное состояние за счет воздействия ПП, которые направлены на снижение пропускной способности общего канала множественного доступа. При этом отличительной особенностью воздействия ПП, переводящих СРС в нестационарное состояние, является периодический характер воздействия.

Модель пакетной радиосети в нестационарном режиме функционирования

Рассмотрим сеть радиосвязи, включающую в себя множество абонентов и канал связи множественного доступа. В сети абоненты генерируют пакеты двух типов: речевой трафик (имеет высокий приоритет обслуживания) и трафик данных (обслуживается после обслуживания речевых пакетов).

Как доказано в [11], при значительном числе абонентов в условиях генерации ими потоков с произвольными законами распределения моментов времени прихода пакетов, суммарный поток пакетов будет пуассоновским. В связи с эти принято допущение о пуассоновском суммарном потоке пакетов.

На одноканальную систему поступают два простейших пуассоновских потока с интенсивностью λ₁ (речь) и λ₂ (данные). Причем поток λ₁ имеет более высокий приоритет и система работает в режиме обслуживания с абсолютным приоритетом. Время обслуживания для каждого потока различно и распределено по экспоненциальному закону с параметрами µ₁ и µ₂, соответственно (см. рис. 3). Марковская цепь, соответствующая обслуживанию системой потоков, находящихся в такой системе, представлена на рис. 4.

Рис. 3. Модель пакетной сети радиосвязи

Рис. 4. Граф переходов состояний системы

Система дифференциальных уравнений, определяющих вероятности состояний данной системы задается в соответствии с [12]:

(1)

Вероятность, что канал свободен от обслуживания, определяется соотношением:

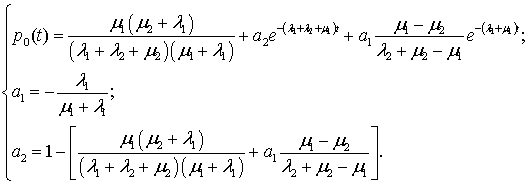(2)

Вероятность, что канал занят обслуживанием пакета первого потока, определяется соотношением:

. (3)

Вероятность того, что канал занят обслуживанием пакета второго потока, определяется соотношением:

. (4)

Решение для стационарного режима получим при условии t→0:

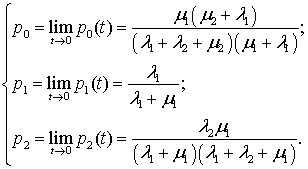. (5)

В этом случае абсолютные ошибки, возникающие во время переходного процесса от допущения о стационарности процесса будут равны:

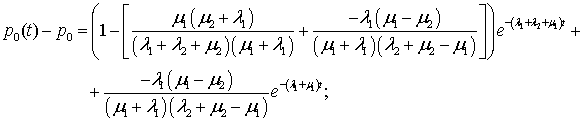
; (6)

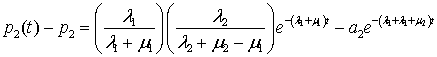Относительные ошибки, возникающие во время переходного процесса, будут определяться как:

. (7)

В период переходного процесса ошибки определения состояния системы довольно значительны. Однако уже при длительности процесса функционирования более 2-3 t_обсл процесс сходится к стационарному режиму, характеристики которого определяются по выражениям (5) - рис. 5.

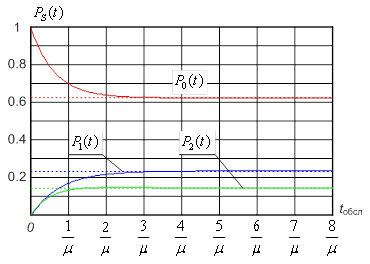
Рис. 5. Вероятности состояния системы в зависимости от времени протекания процесса функционирования канала связи, согласно выражениям (2-4)

При этом относительная погрешность расчета СМО (выражение (7)) с учетом ошибок переходного режима не превышает 5-10 % практически при всем диапазоне загрузок ρ=0,3..0,98 (см. рис. 6).

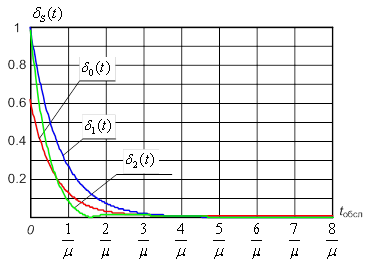
Рис. 6. Относительные ошибки, возникающие во время переходного процесса, согласно выражению (7)

Модель перевода радиосети в нестационарный режим функционирования путем периодического подавления ресурса радиосвязи

Введем допущение о наличие внешнего дестабилизирующего воздействия в виде воздействия на СРС фактора преднамеренных помех (ПП). Исследование, проведенное в работах В. И. Владимирова [6], показывает, что взаимодействие в системе «СРС ‑ постановщик ПП» есть дуэльный конфликт, который носит конфликтно-устойчивый характер и определяется распределением вероятности нахождения СРС в работоспособном состоянии. В связи с этим, за счет применения методик из работ [6] могут быть вычислены вероятности нахождения СРС в работоспособном и «подавленном» состоянии. Однако, в предыдущих работах автора [13, 14] показано, что при использовании описания конфликтно-устойчивого состояния системы «СРС ‑ постановщик ПП» моделей популяционной динамики (моделей Лотки-Вольтерры и Холлинга-Тэннера, описывающих конкуренцию видов «хищник-жертва») поведение данной системы сходится к динамическому фазовому циклу, соответствующему «борьбе за ресурс связи» (рис. 7 фазового цикла). При этом вероятностная модель [6] приобретает динамический характер.

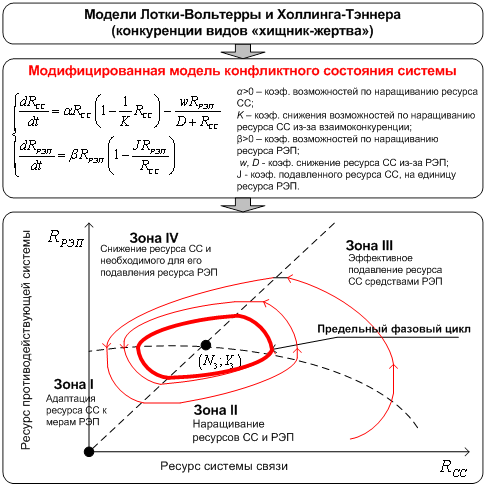
Рис. 7. Динамическое конфликтно-устойчивое поведение системы, описываемое моделями популяционной динамики

Анализ изменения доступного ресурса СРС в составе динамического цикла изменения состояний [13, 14], анализ влияния доступных ресурсов СРС на ее конечную пропускную способность [15] показывает, что функция доступной пропускной способности и соответствующей ей интенсивности обслуживания μ(t) будет иметь квазипериодический вид, который определяется траекторией изменения состояний динамического цикла (рис. 8).

С учетом вышеуказанного, примем допущения о том, что интенсивность μ_max обслуживания СРС под воздействием дестабилизирующего фактора ПП изменяется по периодическому косинусоидальному закону μ(t) (соответствует наиболее простейшему случаю, когда фазовый цикл является проекцией эллипса):

(8)

а так же, что для ведения радиотехнической разведки и вскрытия параметров СРС достаточно времени передачи одного пакета (t_РТР=t_обсл=1/μ_max). Вид законов изменения μ(t) при различных его параметрах приведен на рис. 8.

Рис. 8. Изменение μ(t) в динамическом фазовом цикле изменения состояний системы

В случае изменения μ(t) система уравнений (1), описывающая поведение СРС, примет вид:

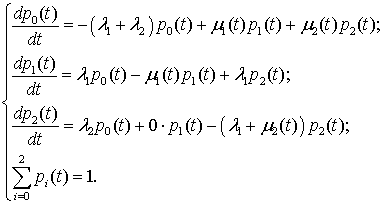. (9)

Аналитическое решение таких систем, в которых интенсивность обслуживания является случайной нестационарной величиной (в связи с этим вероятность перехода в следующие состояние начинает зависеть от времени нахождения в текущем состоянии), представляет известную сложность [11, 15]. В связи с этим для проведения моделирования использовалось численное решение системы (9) методом Рунге-Кутта с использованием оператора rkfixed из пакета MathCAD 14. Моделирование велось с использованием кусочной аппроксимации изменения интенсивности обслуживания СРС μ₁(t) и μ₂(t), при допущении μ₁(t) = μ₂(t).

Исследование системы показало, что основными параметрами, от которых зависит ее поведение являются:

- коэффициент Δ максимального снижения интенсивности обслуживания μ(t) относительно μ_max в динамическом цикле;

- частота f_μ₍_t₎ дестабилизирующего воздействия ПП, выбираемая относительно интенсивности μ_max обслуживания системы.

Проведем моделирование качества функционирования системы от различных характеристик дестабилизирующего воздействия, определяемого временными возможностями вскрытия параметров СРС и возможностями по оперативности наращивания ресурса дестабилизирующего воздействия (Δ и f_μ₍_t₎).

Результаты моделирования

Результаты моделирования поведения сети в зависимости от частоты f_μ₍_t₎ дестабилизирующего воздействия приведены на рис. 9.

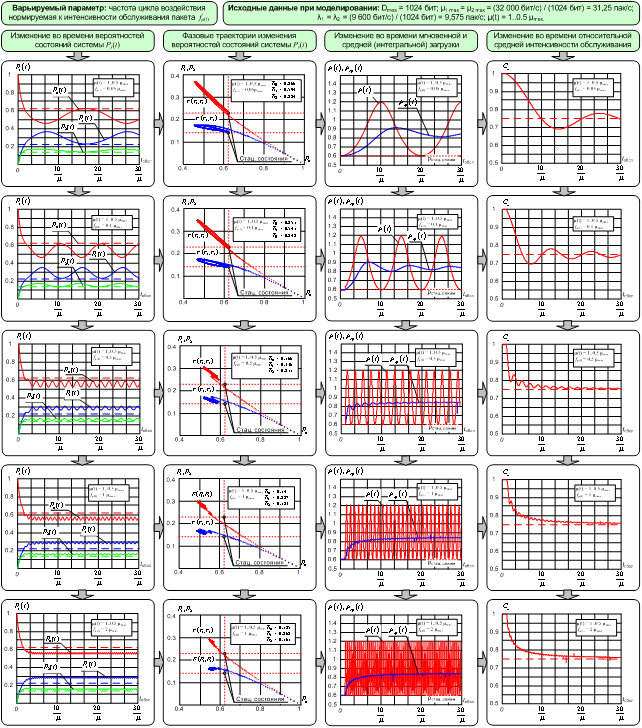
Рис. 9. Результаты моделирования поведения системы в зависимости от частоты воздействия дестабилизирующего фактора f_μ₍_t₎

Анализ результатов моделирования позволяет сделать обоснованный вывод о том, что периодическое изменение интенсивности обслуживания μ(t) переводит систему в нестационарное состояние функционирования. Анализ фазовых траекторий состояний системы (P₀, P₁, P₂), а также максимальных относительных ошибок в определении состояний системы (δ₀, δ₁, δ₂) по сравнению со стационарным состоянием, позволили сделать следующие выводы. Максимальным уровнем подавления обладают воздействия ПП с частотой в десятые и сотые доли от интенсивности облуживания пакетов (f_μ₍_t₎ = (0,5..0,02) μ_max). Таким образом, для эффективного подавления системы пакетной связи достаточная оперативность Т_ПП цикла воздействия источника ПП по снижению качества обслуживания СРС составляет Т_ПП = 2 t_обсл...50 t_обсл (где t_обсл=1/μ_max - длительность обслуживания пакетов в СРС). Проведен анализ мгновенной загрузки системы ρ(t), где , и средней интегральной загрузки системы ρ_ср(t), учитывающей передачу накопленной в буферных устройствах абонентов части пакетов, в моменты кратковременной перегрузки системы (ρ(t)>1):

. (10)

Данный анализ показал, что кратковременная перегрузка системы не ведет к нарастанию средней загрузки системы. Если достаточен объем буферных устройств абонентов, то пакеты, пришедшие в моменты перегрузки системы (ρ(t)>1), передаются в моменты снижения общей загрузки (1<ρ(t)<). Периодическое подавление канала обслуживания (μ_max<μ(t)<0,5μ_max) ведет к логарифмическому росту средней загрузки системы ρ_ср(t), предельный асимптотический уровень которой не зависит от интенсивности воздействия дестабилизирующего фактора. Частота дестабилизирующего воздействия влияет только на длительность достижения предельного уровня.

Аналогичный вывод можно сделать и по анализу относительной средней интенсивности облуживания С_μ. Варьирование μ(t) (μ_max<μ(t)<0,5μ_max) ведет к снижению относительной интенсивности обслуживания С_μот 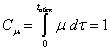[пак. / t_обсл.], до значения [пак. / t_обсл]. Предельный уровень С_μ не зависит от не зависит от интенсивности воздействия дестабилизирующего фактора, а влияет только на длительность сходимости к предельному уровня. Причем, длительность сходимости С_μк предельному значению составляет порядка 10 t_обсл..20 t_обсл при широких пределах варьирования частоты дестабилизирующего воздействия f_μ₍_t₎ = (0,5..0,02) μ_max.

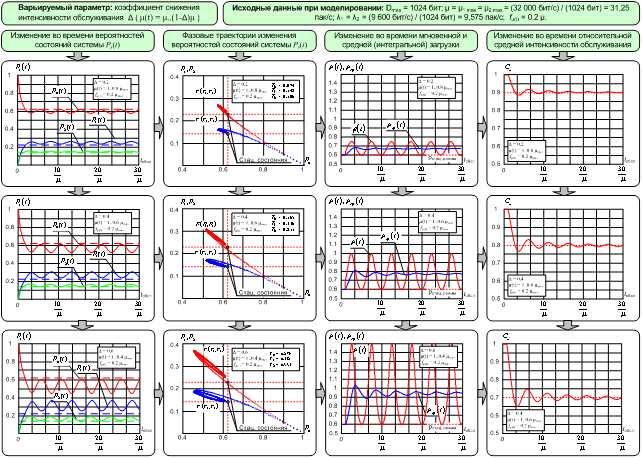
Рис. 10. Результаты моделирования поведения сети при изменении коэффициента Δ определяющего снижение интенсивности обслуживания

На рис. 10 приведены результаты моделирования поведения сети при изменении коэффициента Δ, определяющего максимальный уровень снижения интенсивности обслуживания μ(t) относительно μ_max (выражение (7), рис. 8). Основной вывод, который можно сделать из анализа графических зависимостей, состоит в том, что общей эффект подавления определяется коэффициентом Δ. Уже при Δ=0,6 загрузка системы стремится к ρ_ср→0,95, а относительная интенсивность обслуживания пакетов снижается до С_μ=0,7 пак./t_обсл. Увеличение Δ свыше Δ=0,6 ведет к перегрузке системы и линейному снижению относительной интенсивности обслуживания – рис. 11. При этом зависимость С_μ(Δ) для своего предельного значения можно аппроксимировать выражением:

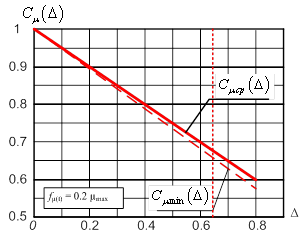
Рис. 11. Зависимости средней загрузки ρ_ср системы и относительной интенсивности С_μ обслуживания пакетов от коэффициента Δ

Необходимо отметить, что изменения параметров частоты f_μ(_t₎ и коэффициента Δ существенно отклоняют состояние системы от стационарного состояния, что можно оценить по фазовым траекториям на рис. 9 и 10. Оценка максимального уровня относительных ошибок при допущении о стационарности состояния системы приведена на рис. 12. Как показывает анализ зависимостей на рис. 12, максимальному воздействию ПП подвержен поток с максимальным приоритетом.

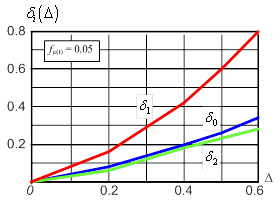
Рис. 12. Максимальные оценки относительных ошибок при допущении о стационарности состояния модели СМО

Выводы

Оптимальными условиями подавления СРС за счет периодического дестабилизирующего воздействия являются воздействия ПП с коэффициентом снижения интенсивности обслуживания Δ=0,5..0,6 и частотой воздействия f_μ₍_t₎ = 0,5 μ_max ..0,02 μ_max (цикл воздействия в этом случае составляет Т_ПП = 2 t_обсл...50 t_обсл), что позволяет снизить относительную интенсивность обслуживания СРС до С_μ≈ 0,7 пак./t_обсл в условиях загрузки СРС ρ_ср≈0,95. Необходимо отметить, что согласно [17-18], СРС со случайным множественным доступом устойчивы в диапазоне нагрузок ρ_ср<0,6, а при превышении пороговой загрузки самопроизвольно переходят в блокированное состояние (именно этот эффект был использован в работе [10] для подавления СРС). Проведенное исследование показало, что для СРС со случайным доступом абонентов и стандартной нагрузкой ρ_ср≈0,4 уже при Δ=0,35..0,48 возникают условия сноса сети в диапазон нагрузок ρ_ср>0,6 и самопроизвольного перехода ее в блокированное состояние.

Полученные результаты, в общем, подтверждают результаты существенного снижения качества обслуживания СМО в переходном и нестационарном режиме. Так, анализ ранее полученных результатов работы С. О. Бурлакова [19] по исследованию переходных режимов работы спутниковой сети связи и ошибок правильного определения состояния сети позволяет сделать следующие выводы. В современных сетях связи имеют место длительные переходные процессы возникающих в результате изменения режимов функционирования и воздействия на СС дестабилизирующих факторов различной природы. В настоящей работе предложено преднамеренное воздействие ПП с вышеуказанными квазиоптимальными параметрами, позволяющее перевести СС в состояние длящегося переходного режима и тем самым снизить ее производительность. В процессе дальнейших исследований предполагается рассмотреть возможность перевода СС в нестационарный режим за счет варьирования интенсивности входных информационных потоков.

Литература

1. Макаренко С. И. Анализ возможностей подавления объединенных сетей связи // Молодежь. Техника. Космос: труды IV Общероссийской молодежной науч.-техн. конф./ Балт. гос. техн. ун-т. – СПб.; 2012. – С. 288-290.

2. Исаков Е. Е. Устойчивость военной связи в условиях информационного противоборства. - СПб.: Изд. Политехн. ун-та, 2009. – 400 с.

3. Куприянов А. И., Сахаров А. В. Теоретические основы радиоэлектронной борьбы: Учебное пособие. – М.: Вузовская книга, 2007. – 356 с.

4. Современная радиоэлектронная борьба. Вопросы методологии / под ред. Радзивского В. Г. – М.: «Радиотехника», 2006. - 424 с.

5. Радзиевский В. Г., Сирота А. А. Теоретические основы радиоэлектронной разведки. 2-е изд. – М.: Радиотехника, 2004. – 432 с.

6. Владимиров В. И. Информационные основы радиоподавления линий радиосвязи в динамике радиоэлектронного конфликта: монография – Воронеж: ВИРЭ, 2003. – 275 с.

7. Назаров А. Н., Сычев К. И. Модели и методы расчета показателей качества функционирования узлового оборудования и структурно-сетевых параметров сетей связи следующего поколения. – Красноярск: изд. ООО «Политком», 2010. – 389 с.

8. Лялюк И. Н. Системы связи, АСУ и разведки вооруженных сил США. – М.: изд. ВАТУ им. Н. Е. Жуковского, 2000.

9. Денисов Б. Б. О проблемах наращивания телекоммуникационного ресурса в интересах функционирования информационно-управляющей системы специального назначения // Доклады конференции «Современные тенденции развития теории и практики управления в системах специального назначения» - М.: ОАО «Системпром», 2012. – С. 21-24.

10. Макаренко С. И. Подавление пакетных радиосетей со случайным множественным доступом за счет дестабилизации их состояния // Журнал радиоэлектроники, 2011, № 9. - URL: jre.cplire.ru/jre/sep11/4/text.pdf

11. Вентцель Е. С. Введение в исследование операций - М.: Советское радио, 1964. – 391 с.

12. Новиков О. А., Петухов С. И. Прикладные вопросы теории массового обслуживания. – М.: Сов. радио, 1969. – 400 с.

13. Макаренко С. И. Моделирование совместного использования ресурсов системы связи методами популяционной динамики // Вестник ВГТУ, 2010, т. 6, № 9. с. 63-65.

14. Макаренко С. И. Модели воздействия средств радиоэлектронной борьбы на систему связи на основе методов популяционной динамики // Вестник ВГТУ, 2011, т.7, № 1, с. 96-99.

15. Макаренко С. И. Исследование влияния преднамеренных помех на возможности по ретрансляции сообщения и показатели качества обслуживания канального уровня модели OSI для системы связи со случайным множественным доступом абонентов // Информационные технологии моделирования и управления, 2010, №6 (65). с. 807-815. – URL: www.sbook.ru/itmu/itmu.htm

16. Смагин А. В. Немарковские задачи теории надежности. – М.: Минобороны СССР, 1982. – 269 с.

17. Бертсекас Д., Галлагер Р. Сети передачи данных. – М.: Мир, 1989. – 544 с.

18. Пасечников И. И. Методология анализа и синтеза предельно нагруженных информационных сетей. Монография. – М.: Машиностроение-1, 2004. - 147 с.

19. Бурлаков С. О., Ершов Г. А., Журавлев Д. А. Анализ нестационарного режима работы сети спутниковой связи // Приборы и системы. Управление, контроль, диагностика. - 2011. - N 1. - С. 10-15.