ОЦЕНКА МОЩНОСТИ ИНТЕРМОДУЛЯЦИОННЫХ ПОМЕХ ПРИ ПРЕДЕЛЬНОМ ОГРАНИЧЕНИИ ОГИБАЮЩЕЙ СИГНАЛОВ С ОРТОГОНАЛЬНЫМ ЧАСТОТНЫМ МУЛЬТИПЛЕКСИРОВАНИЕМ
Л. Е. Назаров ¹, А. С. Зудилин ²
¹ Институт радиотехники и электроники им. В.А.Котельникова РАН, г. Фрязино
² ОАО “Российские космические системы”, г. Москва
Получена 29 мая 2013 г.
Аннотация. Приведены методики оценивания мощности интермодуляционных помех при предельном ограничении огибающей сигналов с частотным ортогональным мультиплексированием на выходе передатчика как нелинейного устройства.
Ключевые слова: нелинейности передатчика, OFDM сигналы, интермодуляционные помехи.
Abstract. This paper presents the technique of intermodulation noise power evaluation for OFDM signals with complex envelope limit clipping to compensate the nonlinear distortions caused by HPA (high power amplifier).
Key words: nonlinear power amplifier, OFDM signals, AM/AM and AM/PM characteristics, intermodulation noise.
Введение
Сигналы с ортогональным частотным мультиплексированием известны в литературе как OFDM сигналы (orthogonal frequency-division multiplexing) [1,2,3]. Эти сигналы обладают рядом свойств, определяющих перспективность их применения в системах передачи дискретных сообщений. В частности, OFDM сигналы используются для передачи информации по каналам с многолучевостью, которая обуславливает частотно-селективные замирания сигналов. Данный подход составляет альтернативу известным методам борьбы с многолучевостью, включая RAKE приемник и прием с оценкой импульсной характеристики канала [4,5].
OFDM сигналы являются базовыми для ряда принятых протоколов, например, IEEE 802.11 (WiFi), IEEE 802.16 (WiMax), DVB-SH (цифровое спутниковое телевещание), 3GPP LTE (мобильная связь 4G).
Недостатком OFDM сигналов является большие значения пик/фактор, то есть непостоянство огибающих сигналов [3], что приводит к появлению интермодуляционных помех на выходе передатчика как нелинейного устройства, работающего в номинальном режиме.
С целью уменьшения значений пик/фактор применяется предискажение OFDM сигналов путем ограничения их огибающей с сохранением фаз, порог ограничения определяется уровнем насыщения передатчика.
В данной работе приведены методики оценивания мощности интермодуляционных помех (общей мощности помех и мощности помех в полосе сигналов) для предельного ограничения огибающей OFDM сигналов, наиболее простого при реализации. Полученные формульные соотношения доказаны в предположении эквивалентности OFDM сигналов случайному стационарному гауссовскому процессу.
Приведена методика оценивания энергетических потерь при применении OFDM сигналов по отношению к сигналам с постоянной огибающей при использовании которых возможна работа усилителей с номинальной мощностью без интермодуляционных помех. С использованием данной методики произведены численные оценки энергетических потерь для ряда схем помехоустойчивого кодирования в сочетании с OFDM сигналами.
1. Постановка задачи
OFDM сигналы представляют сумму 
составляющих гармонических сигналов,
ортогональных на интервале времени определения 
[1,2,3]
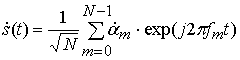. (1)
Значения символов 
объемом 
определяются
используемым сигнальным “созвездием”. Ниже рассматриваются “созвездия”
ФМ4 (
). Ортогональность составляющих сигналов
обеспечивается выбором частот 
для двумерных
сигналов.
На вход передатчика поступает
узкополосный сигнал 
. Здесь 
,
- огибающая и фаза сигнала, 
- несущая частота, мощность сигналов 
равна 
.
Параметр сигналов, который определяет динамический
диапазон их огибающей, является пик/фактор 
[6]. OFDM сигналы
характеризуются высокими значениями
, для составляющих сигналов с “созвездием” ФМ-4 верно
соотношение 
. Это приводит к амплитудным и фазовым
искажениям OFDM сигналов и
появлению интермодуляционных помех на выходе передатчика как нелинейного
элемента в режиме номинальной мощности и, как следствие, к энергетическому
проигрышу по отношению к сигналам с постоянной огибающей.
Суть решаемой проблемы - разработка методик оценки мощности интермодуляционных помех, соответствующих моделям нелинейностей передатчика.
2. Модели нелинейностей
Известные модели нелинейностей передатчиков амплитуда/амплитуда (АМ/АМ) и амплитуда/фаза (АМ/ФМ) можно отнести к двум общим классам. К первому классу относятся динамические модели, учитывающие инерционность нелинейностей (модель в виде рядов Вольтера, модель Винера, модель Хаммерштейна [7]).
Модели, представляющие
передатчики в виде безинерционных нелинейных устройств, относятся ко второму
классу. Широко используемая модель из данного класса связывает комплексную
амплитуду сигнала на выходе передатчика 
с комплексной амплитудой входного сигнала 
[7]
. (2)
Здесь 
- нелинейности АМ/АМ и АМ/ФМ
соответственно.
Для передатчиков (например,
на основе лампы бегущей волны) модельные представления имеют
вид [7]
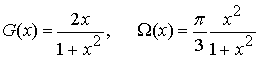. (3)
Значения огибающих нормированных сигналов на выходе
передатчика в точке насыщения равны 1 (
).
Амплитудные и фазовые искажения нарушают ортогональность составляющих сигналов в (1), вследствие чего возникают интермодуляционные помехи, добавляемые к канальным помехам. Это снижает помехоустойчивость данных сигналов по отношению к сигналам с постоянной огибающей.
Методы снижения влияния нелинейностей основаны на линеаризации высокочастотного тракта передачи, на снижении мощности сигналов на входе передатчика с целью задания его режима работы, близком к линейному режиму, а также на снижении значений пик/фактор OFDM сигналов [8].
Суть методов линеаризации
- амплитудное и фазовое предискажение сигналов на входе передатчика 
с целью компенсации амплитудной и фазовой
нелинейностей передатчика. Для модели (2), (3) функции 
являются
решениями системы уравнений [9]
, (4)
. (5)
Этот подход позволяет компенсировать фазовые
искажения, однако амплитудные искажения могут быть компенсированы лишь в
рабочей области до точки насыщения. Поэтому с целью снижению
мощности интермодуляционных помех уменьшают мощность 
входных OFDM сигналов
по отношению к максимальной мощности 
, а также применяют методы
предискажения для снижения пик/фактор сигналов. Здесь
- нормированная амплитуда огибающей
сигналов на выходе передатчика в точке насыщения.
В классе методов снижения пик/фактора наиболее эффективным является ограничение огибающей OFDM сигналов с сохранением фаз [9,10]
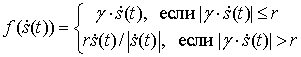. (6)
Порог ограничения для
нормированных сигналов равен 
. Условие (6) определяет формирование OFDM сигналов на выходе ограничителя с максимальной огибающей 
. Здесь
– коэффициент, определяющий крутизну
линейного участка, при 
функция нелинейности 
соответствует предельному ограничению огибающей.
Ниже приведены методики оценивания общей мощности интермодуляционных помех и мощности данных помех в рабочей полосе для предельного метода ограничения (7) при формировании OFDM сигналов.
3. Оценки общей мощности интермодуляционных помех и мощности сигнальной составляющей
Методика оценки общей
мощности интермодуляционных помех и мощности сигнальной составляющей для
нелинейности 
основана
на представлении комплексной огибающей выходного сигнала , соответствующего входному комплексному сигналу
, в виде [11]
. (7)
Здесь 
-
интермодуляционные помехи. Постоянная 
задается
условием минимума среднеквадратичного отклонения 
, 
- операция усреднения по ансамблю
сигналов. При этом выполняется условие ортогональности 
,
задается соотношением 
[11]. Здесь 
-
операция комплексного сопряжения.
При 
OFDM сигналы
эквивалентны случайному стационарному гауссовскому процессу с одномерным
Релеевским законом плотности распределения огибающей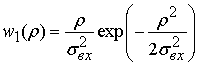 
[3].
Для нелинейности (7) постоянная является вещественной
. (8)
Для предельного
ограничения имеем 
и мощность 
выходных реальных OFDM сигналов равна
. (9)
Для предельного
ограничения огибающей мощность реального процесса 
равна 
, для полной мощности интермодуляционных
помех справедливо соотношение 
. В этом случае
отношение сигнал/помеха равно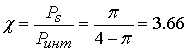 
(5.6
дБ).
Следует отметить также,
что при предельном ограничении огибающей OFDM сигналов 21.5% (или (1-
)100%)
от общей номинальной мощности передатчика идет на излучение интермодуляционных
помех.
4. Оценка мощности интермодуляционных помех в полосе OFDM сигналов
Оценивание
мощности интермодуляционных помех в полосе OFDM сигналов основано на
вычислении спектральной плотности данных помех путем преобразования Фурье
корреляционной функции 
для квадратурного канала.
Обоснование этого подхода основано на статистической независимости квадратурных
компонент OFDM сигналов, рассматриваемых как случайный стационарный гауссовский
процесс.
Корреляционная
функция 
на выходе нелинейности 
для квадратурной
компоненты узкополосных OFDM сигналов
имеет вид [12]
,
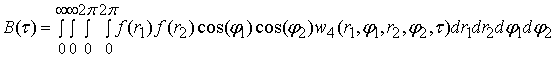(10)
-
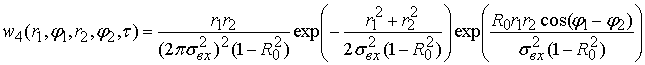двумерная плотность совместного распределения огибающей и фазы для узкополосных
OFDM сигналов с полосой 
, 
- нормированный
коэффициент корреляции OFDM сигналов на видеочастоте.
Выражение (10) после преобразований может быть записано в виде
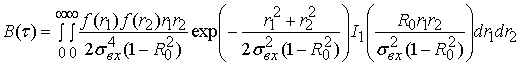. (11)
Здесь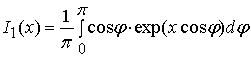 
– функция Бесселя первого порядка.
Справедливо соотношение [13]
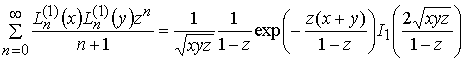. (12)
Здесь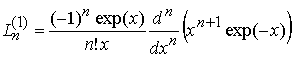 
- полиномы Лагерра 1-го порядка.
Введем обозначения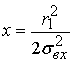 
, 
, 
, подставляя которые в (12), получаем
выражение для
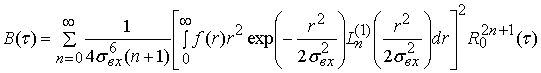. (13)
Слагаемое в (13),
содержащее 
(
),
соответствует составляющей квадратурной компоненты OFDM сигналов.
Сумма (13)
для 
определяет мощность интермодуляционных
помех квадратурной компоненты в полосе OFDM сигналов.
Спектральная плотность интермодуляционных
помех 
в полосе OFDM сигналов может быть определена путем преобразования
Фурье корреляционной функции (13).
В случае предельного
ограничения при 
средняя мощность квадратурных
компонент OFDM сигналов при в
(13) равна
?,
что совпадает с приведенным значением (9)
для мощности выходных реальных OFDM сигналов.
Мощность
интермодуляционных помех в полосе OFDM сигналов, вычисленная с использованием суммы (13) для , равна 
. Соответствующее значение
сигнал/помеха равно 
(8.5
дБ), что на 2.9 дБ превышает соответствующее значение
сигнал/помеха 
с учетом общей мощности
интермодуляционных помех 
.
Спектральная плотность интермодуляционных
помех в полосе OFDM сигналов может быть определена путем преобразования
Фурье корреляционной функции [12]. При этом спектральная плотность 
, соответствующая корреляционной функции 
, может быть вычислена с использованием
свертки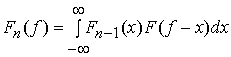 
.
На рис.1
приведена зависимость отношения сигнал/помеха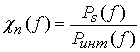 
от
частоты как отношение спектральных плотностей мощностей OFDM сигналов и
интермодуляционных помех, вычисленные с использованием приведенной методики. По
оси абсцисс отложены значения частоты, нормированные на полосу OFDM сигналов. Видна неравномерность спектральной плотности
мощности интермодуляционных помех в полосе сигналов - различие в центре и по
краям полосы достигает 1.6 дБ.
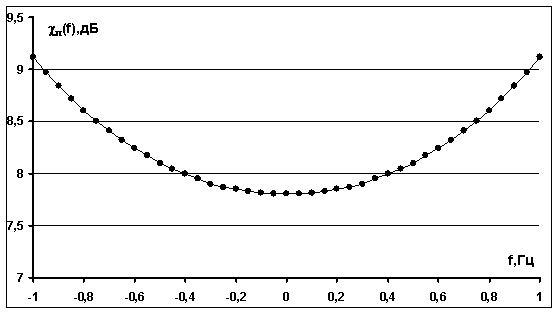
Рис.1 Зависимость
отношения сигнал/помеха 
от частоты как
отношение спектральных плотностей мощности OFDM сигнала и мощности
интермодуляционной помехи.
5. Оценка энергетического проигрыша OFDM сигналов по отношению к сигналам с постоянной огибающей
Для сигналов с постоянной
огибающей возможна работа передатчика в режиме насыщения без возникновения
интермодуляционных помех. Для OFDM сигналов
требуется повышение мощности передатчика по отношению к сигналам с постоянной
огибающей с целью компенсации интермодуляционных помех и обеспечения требуемого
значения сигнал/помеха 
при приеме
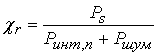. (14)
Здесь 
-
мощность тепловых шумов в канале, полагаемых некоррелированными с интермодуляционными
помехами, 
- средняя мощность интермодуляционных
помех в полосе OFDM сигналов, 
- мощность OFDM сигналов.
Пусть 
- мощность передатчика в номинальном
режиме, требуемая для передачи информации с вероятностью ошибки на
информационный бит 
по каналу с мощностью тепловых
шумов с использованием сигналов ФМ4 с
постоянной огибающей. Для передачи информации с эквивалентной вероятностью ошибки
с использованием OFDM сигналов с предельным ограничением огибающей при их
формировании необходимо увеличить мощность передатчика в номинальном режиме до 
. Отношение 
является
оценкой энергетического
проигрыша для OFDM сигналов по отношению к ФМ4
сигналам.
Для ФМ4 в
сочетании с помехоустойчивым кодом с кодовой скоростью 
справедливо соотношение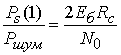 
[6]. Здесь 
- энергия сигналов на бит, 
- спектральная
плотность тепловых шумов. Значение 
определяется вероятностью ошибки
для используемого кода. На основе этого
равенства можно получить
аналитическое выражение относительно оценки энергетического проигрыша 
для OFDM сигналов с предельным ограничением огибающей по отношению к
сигналам ФМ4 с постоянной огибающей. При выводе соотношения используется
исходное выражение (14) с учетом приведенного выше значения
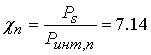
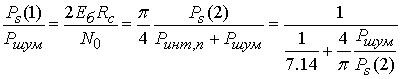. (15)
Из
(15) имеем результирующее выражение относительно
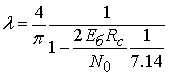. (16)
Для вероятности ошибки 
с использованием сверточного кода с
кодовой скоростью 
и длиной кодового ограничения 7
необходимо обеспечить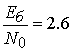 
(4.15 дБ) [6]. В этом случае энергетический проигрыш
оценивается значением 
дБ.
Для вероятности ошибки с использованием сверточного турбо-кода с
кодовой скоростью необходимо обеспечить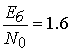 
(2 дБ) [4]. Энергетический проигрыш оценивается значением 
дБ.
При уменьшении кодовой
скорости соответствующие энергетические потери уменьшаются
до предельного значения 1.1 дБ.
Заключение
Приведены результаты по разработке методов оценивания мощности интермодуляционных помех для OFDM сигналов на выходе передатчика как нелинейного устройства. Недостатком рассматриваемых OFDM сигналов является большие значения пик/фактор, то есть непостоянство огибающих сигналов, что приводит к появлению интермодуляционных помех на выходе нелинейностей. Рассмотрен метод предискажения OFDM сигналов при их формировании с целью уменьшения значений пик/фактор - предельное ограничение огибающей OFDM сигналов с сохранением фаз.
Для этой нелинейности приведены методики оценивания мощности интермодуляционных помех (общей мощности и мощности в полосе сигналов) и мощности сигнальной составляющей. Основу данных методик составляют методы нелинейных безинерционных преобразований случайных гауссовских процессов, к которым можно отнести OFDM сигналы с большим числом составляющих сигналов. Значение сигнал/помеха в полосе сигналов равно 8.5 дБ, что на 2.9 дБ превышает соответствующее значение сигнал/помеха с учетом общей мощности интермодуляционных помех.
Приведены
значения оценок энергетического
проигрыша OFDM сигналов по отношению к сигналам с
постоянной огибающей для различных схем помехоустойчивого кодирования.
Показано, что для наиболее эффективных помехоустойчивых кодов (например, для
турбо-кодов с кодовой скоростью 0.5) значение энергетического
проигрыша не превышает 2.15 дБ. При уменьшении кодовой скорости соответствующие энергетические потери монотонно
уменьшаются до предельного значения 1.1 дБ.
Показана неравномерность спектральной плотности мощности интермодуляционных помех в полосе OFDM сигналов при применении предельного ограничения огибающей - различие в центре и по краям полосы достигает 1.6 дБ.
Литература
1. Вишневский В.М., Ляхов А.И., Портной С.Л., Шахнович И.В. Широкополосные сети передачи. М.: Техносфера. 2005.
2. Волков Л.Н., Немировский М.С., Шинаков Ю.С. Системы цифровой радиосвязи. Базовые методы и характеристики. 2005. Москва. Эко-Трендз.
3. Liu H., Li G. OFDM-Based Broadband Wireless Networks. A John Wiley & Sons. New Jersey. 2005.
4. Скляр Б. Цифровая связь. Теоретические основы и практическое применение. М.: Издательский дом «Вильямс». 2003.
5. Витерби А.Д., Омура Дж.К. Принципы цифровой связи и кодирования. М.: Радио и связь. 1982.
6. Зюко А.Г., Фалько А.И., Панфилов И.П., Банкет В.Л., Иващенко П.В. Помехоустойчивость и эффективность систем передачи информации. М.:Радио и связь. 1985.
7. Saleh A.A.M., Salz J. Adaptive Linearization of Power Amplifiers in Digital Radio Systems.// The Bell System Technical Journal. 1983. Vol.62. N4. P.1019-1033.
8. Lim D., Heo S., No J. An Overview of Peak-to-Average Power Ratio Reduction Schemes for OFDM Signals.// Journal of Communication and Networks. 2009. V.11. N3. June. P. 229-239.
9. Benedetto M-G.D., Mandarini P. An Application of MMSE Predistortion to OFDM Systems.// IEEE Transactions on Communications. 1996. Vol.44. N11. P.1417-1420.
10. Назаров Л.Е., Зудилин А.С. Оценивание мощности интермодуляционных помех для сигналов с ортогональным частотным мультиплексированием. // Телекоммуникации, 2013. №1. Стр. 21-26.
11. Шахтарин Б.И. Случайные процессы в радиотехнике. Часть 1. Линейные системы. М.: Радио и связь. 2002.
12. Левин Б.Р. Теоретические основы статистической радиотехники. Книга первая. М.:Сов. радио. 1969.
13. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Наука. 1971.