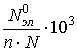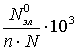УДК 621.391

ВОССТАНОВЛЕНИЕ ГРУППОВОГО СИГНАЛА ПРИ ВОЗДЕЙСТВИИ  ИМПУЛЬСНЫХ ПОМЕХ

В. А. Вершинин

Рыбинский государственный авиационный технический университет им. П. А. Соловьева

 

Получена 5 марта 2013 г., после доработки 16 мая 2013 г.

 

Аннотация. В работе рассматривается групповая передача двоичных сообщений с использованием преобразования Уолша. Определены параметры группового сигнала и характеристики дискретного канала связи при наличии импульсных помех. Исследован способ восстановления группового сигнала, позволяющий существенно уменьшить вероятность ошибки при передаче. Приведены результаты моделирования.

Ключевые слова: групповая передача, преобразование Уолша, импульсные помехи, восстановление сигнала.

Abstract: In the paper the group the transmission of binary messages using transformations of Walsh. Settings are defined group of the signal and the characteristics of the discrete channel of communication in the presence of impulse noise. Investigated the method of recovery of group of the signal, which allows to significantly reduce the probability of error in transmission. Given the results of the simulation.

Key words: group transfer, Walsh conversion, impulse noise, the restoration of the signal.

 

1. Последовательная и групповая передача сообщений

Последовательная передача двоичных сообщений заключается в следующем. Каждый элемент сообщения может принимать два значения 0 или 1. Элементы сообщения поступают в модулятор, где преобразуются в последовательность элементарных сигналов, каждый из которых имеет длительность . В простейшем случае элементарный сигнал представляет собой  прямоугольный импульс длительностью  и величиной  плюс  или минус  в зависимости от значения (0 или 1) элемента сообщения. Если элементарные сигналы представляют собой импульсы напряжения, то  измеряется в вольтах. Таким образом, передача последовательности из n элементов сообщения занимает время . Из модулятора элементарные сигналы поступают в линию связи и далее в демодулятор. В демодуляторе осуществляется обработка элементарных сигналов с целью определения значений элементов принятого сообщения. Из-за помех в линии связи последовательность элементов принятого сообщения может содержать неверно принятые элементы (ошибки).

Рассмотрим групповую (параллельную) передачу двоичных сообщений. В модуляторе сообщение разбивается на блоки по n элементов. Каждому блоку ставится в соответствие информационный вектор  с числом элементов n. Элемент информационного вектора  () принимает значение +1 или –1 в зависимости от значения соответствующего элемента блока (0 или 1). Информационный вектор преобразуется в групповой вектор  с помощью преобразования Уолша:

 

,                                                                                                                 (1)

 

где  – матрица Уолша порядка n.

Матрица Уолша является частным случаем матрицы Адамара при , где . В качестве примера можно привести матрицу Уолша при :

 

 

Элемент группового вектора  () может принимать  значение: –n, , , …, –4, –2, 0, 2, 4, …, , , n. В модуляторе на основе группового вектора  формируется групповой сигнал, поступающий в линию связи. Групповой сигнал представляет собой последовательность из n элементов. Элемент группового сигнала с номером l соответствует элементу группового вектор . В простейшем случае, который и будем рассматривать в дальнейшем, l-й элемент группового сигнала представляет собой  прямоугольный импульс длительностью  и величиной , где B – постоянная величина, . Если элементы группового сигнала представляют собой импульсы напряжения, то B измеряется в вольтах. Таким образом, групповой сигнал имеет длительность  и носит ступенчатый характер. Из модулятора групповой сигнал поступает в линию связи и далее в демодулятор. В демодуляторе осуществляется обработка группового сигнала с целью определения блока элементов принятого сообщения. Из-за помех в линии связи  в общем случае блок элементов принятого сообщения может содержать неверно принятые элементы (ошибки).

Будем считать, что при прохождении линии связи групповой сигнал подвергается воздействию импульсных помех. В результате s элементов группового сигнала оказываются искаженными. Будем также считать, что различные варианты расположения искаженных элементов на интервале формирования группового сигнала равновероятны и что известны номера искаженных элементов группового сигнала.

Для уменьшения влияния импульсных помех используется бланкирование. При этом в демодуляторе из группового сигнала формируется групповой вектор . Элементы этого вектора, соответствующие искаженным элементам группового сигнала, принимаются равными нулю, эти элементы будем называть также искаженными. Элементы , соответствующие неискаженным элементам группового сигнала,  равны соответствующим элементам группового вектора c. После формирования вектора  определяется вектор . Нетрудно показать с учетом (1), что при отсутствии помех в линии связи . При наличии  помех в общем случае .

По элементам вектора  определяется принятый информационный вектор , элементы которого

,

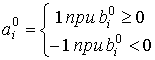и принятый блок элементов двоичного сообщения.

Более эффективно уменьшить влияние импульсных помех можно путем восстановления элементов группового сигнала [1]. При этом восстановлению подлежат искаженные элементы группового вектора , полученного в результате бланкирования. Процесс обработки группового сигнала в демодуляторе занимает несколько этапов. Номер этапа обозначим   . На каждом этапе формируется вектор  ,  и , причем

,                                                                                                  (2)

.

 

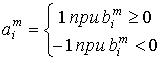На начальном этапе ()  формируется  (см.  выше). На следующих этапах  ()  вектор  формируется из вектора  путем замены (восстановления) искаженных элементов этого вектора соответствующими элементами вектора . Процесс продолжается до такого значения , при котором  .  При этом вектор   считается принятым информационным вектором, на основании которого определяется  принятый блок элементов двоичного сообщения.

 

2. Параметры группового сигнала

Пусть элементы блока передаваемого сообщения являются независимыми случайными величинами, каждая из  которых с равной вероятностью принимает значения 0 либо 1. Тогда некоторый элемент группового вектора  является дискретной случайной величиной, которая может принимать значения, , , , …, , , , , , …, , , . Можно записать, что ,.

Случайная величина  имеет биномиальное распределение и принимает возможные значения с вероятностью , где  – биномиальный коэффициент. Математическое ожидание значения элемента группового вектора равно ,

 

 а его дисперсия  .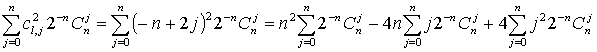

Учитывая, что 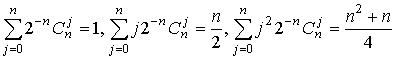, нетрудно получить значение дисперсии, равное n.

Элемент группового сигнала в соответствии со значениями элемента группового вектора может принимать значения . Его также можно рассматривать как случайную величину с нулевым математическим ожиданием и дисперсией (средней мощностью) . Нетрудно также получить, что энергия группового сигнала равна . Пиковое значение элемента группового сигнала (максимум абсолютной величины значения) равно , среднеквадратичное . Чтобы энергия, затрачиваемая на передачу n элементов сообщения при последовательной и групповой передаче, была одинаковой, должно быть .

Можно показать, что  различные элементы группового вектора являются некоррелированными, но зависимыми случайными величинами и что энтропия группового вектора или группового сигнала (среднее количество информации, приходящееся на элемент) .

 

3. Информационные характеристики канала связи

Рассмотрим дискретный канал связи, на вход которого поступают элементы некоторого сообщения, представляющие собой, в отличие от элементов группового вектора, независимые случайные величины. Обозначим элемент сообщения x, он может принимать значения: , , , …, , , , , , …, , , . Можно записать, что ,. Вероятности этих значений соответствуют биномиальному закону распределения:

 

.                                                                                                         (3)

 

Пусть далее на выходе канала связи элементу сообщения x соответствует элемент y, который может принимать значения , , , …, , , , , , …, , , . Можно записать, что , . Из-за импульсных помех в канале в каждой последовательности из n элементов y имеется s искаженных элементов по сравнению с соответствующими элементами x. Искаженные элементы имеют нулевое значение и различные варианты расположения искаженных элементов в последовательности из n элементов равновероятны. Тогда случайная величина y принимает возможные значения с вероятностью

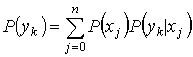,                                                                                          (4)

 

где  – вероятность значения  случайной величины y, если известно, что случайная величина x приняла значение . Для данной модели помехи

 

                                                                      (5)

 

Как показано в [2], количество информации, передаваемое по такому каналу можно определить по формуле:

 

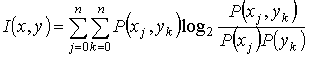.                                                                (6)

 

Здесь  определяется по формуле (3),  – по формуле (4) с учетом (5).  – вероятность того, что случайная величина x примет значение , а случайная величина y – значение , эта вероятность определяется с использованием (3) и (5) по известной формуле: .

В качестве примера при  и n, равных 16, 32, 64, 128, 256. 512 по формуле (6) можно получить следующие значения  соответственно: 2.4810, 2.9322, 3.3882, 3.8462, 4.3043, 4.7610 бит/элемент. Как было отмечено в конце раздела 2, энтропия группового вектора , следовательно, групповой вектор по отношению к рассмотренному выше каналу связи обладает существенной избыточностью, которая растет с увеличением n при постоянном значении . Избыточность эта связана с тем, что элементы группового вектора являются зависимыми случайными величинами. Эта избыточность используется при описанном выше восстановлении элементов группового вектора.

 

4. Оценка помехоустойчивости

Пусть на начальном этапе вектор  содержит s искаженных элементов и r принимает значения номеров искаженных элементов вектора . Тогда при фиксированном значении элемента вектора a с номером I  соответствующий элемент вектора  на основании (2) можно представить следующим образом: , где  –  элемент i-ой строки и r-го столбца матрицы . При достаточно больших n эту величину можно считать распределенной по нормальному закону с математическим ожиданием и дисперсией соответственно:  и . Исходя из этого, вероятность ошибки при определении элемента вектора  можно оценить по формуле:

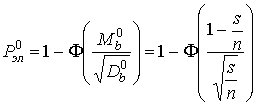,                                                                          (7)

где .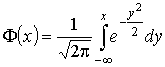

 

Пусть далее на некотором m-ом этапе () вектор  содержит s восстановленных элементов. Тогда восстановленный элемент с номером r   имеет значение: 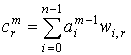. Последнее выражение может быть записано в виде:

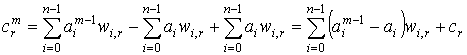. Тогда при фиксированном значении элемента вектора a с номером I  соответствующий элемент вектора  на основании (2) можно представить следующим образом:

 

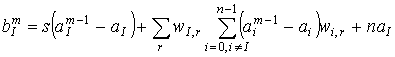.                                            (8)

 

Поскольку элементы вектора a считаются независимыми случайными величинами,  принимающими с равной вероятностью значения 1 и –1, входящая в (8) случайная величина  может принимать значения –2, 0, 2 с вероятностью  , ,  соответственно. Ее математическое ожидание равно нулю, а дисперсия . Здесь  – вероятность ошибки определения элемента вектора . Входящая в (8) случайная величина  принимает значения 0 и  с вероятностью  и  соответственно, ее математическое ожидание равно , дисперсия . При достаточно больших значениях n будем считать некоррелированными слагаемые, входящие во внутреннюю и внешнюю суммы выражения 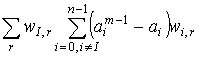, а также слагаемые  и 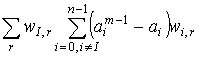. Тогда можно определить математическое ожидание  и дисперсию  случайной величины , определяемой согласно (8):

,

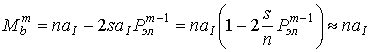. Используя неравенство Чебышева, можно получить, что

 

.                                                                            (9)

Отметим, что последнее выражение получено для  и . Из (7) можно получить, что при  значение , поэтому будем считать, что  неравенство  выполняется при . Тогда из (9) следует, что для  значение . Следовательно, при достаточно больших n и (см. раздел 1) величина .

 

5. Моделирование групповой передачи

В среде Matlab было проведено моделирование групповой передачи с восстановлением искаженных элементов группового вектора. Осуществлено два вида моделирования.

При моделировании первого вида предполагалось, что при заданном n число искаженных элементов группового вектора s является детерминированной величиной, причем . Число испытаний (число переданных векторов a) равно . Передаваемые векторы формировались функцией randsrc(1,n), векторы искаженных элементов – функцией randerr(1,n,s). Результаты приведены в таблице 1. Здесь  – число ошибочно принятых элементов векторов ;  – оценка вероятности ошибки ; – число ошибочно принятых векторов ; – число ошибочно принятых элементов  векторов ; – число ошибочно принятых векторов . Заметим, что условия моделирования первого вида полностью соответствуют допущениям, принятым в предыдущих разделах. Кроме того,  фактически являются вероятностью ошибки при передаче без восстановления элементов группового вектора, когда используется только бланкирование (обнуление элементов группового вектора, соответствующих искаженным элементам группового сигнала).

 

Таблица 1.

n
16	1248056	7.8004	155358	1248056	155358
32	1816082	5.6753	404782	309280	37653
64	3062327	4.7849	1356573	36449	4324
128	5651498	4.4152	2906541	116	10
256	10854508	4.2400	5093783	0	0
512	21277824	4.1558	7638307	0	0

 

При моделировании второго вида предполагалось, что при заданном n число искаженных элементов группового вектора s является случайной величиной, распределенной по закону Пуассона с математическим ожиданием S, причем . Число испытаний (число переданных векторов a) равно . Передаваемые векторы формировались функцией randsrc(1,n), число s  искаженных элементов группового вектора определялось функцией poissrnd(S), векторы искаженных элементов формировались функцией randerr(1,n,s). Результаты приведены в таблице 2.

 

Таблица 2.

n
16	3178256	19.864	855600	2055751	429393
32	3554154	11.107	1148298	823877	155393
64	4759228	7.4363	1861899	175869	25812
128	7343171	5.7369	3084333	8699	1005
256	12549554	4.9022	4934992	27	2
512	22967128	4.4858	7271766	0	0

 

5. Выводы

В условиях действия рассмотренных моделей импульсной помехи при использовании алгоритма восстановления групповая передача двоичных сообщений позволяет сделать сколь угодно малой вероятность ошибки.

Уменьшение вероятности ошибки достигается при увеличении длительности группового сигнала без снижения скорости передачи элементов двоичного сообщения, при постоянной энергии, затрачиваемой на передачу элемента двоичного сообщения, неизменной полосе частот, занимаемой групповым сигналом.

 

Литература

1.     А. с. 1100743 (СССР) МКИ³ H 04 J 3/00.

2.     Теория электрической связи: Учебник для вузов /  А. Г. Зюко, Д. Д. Кловский, В. И. Коржик, М. В. Назаров; Под ред. Д. Д. Кловского. – М. : Радио и связь, 1998. – 432 с.