УДК 621.396
Особенности применения инверсной фильтрации для восстановления изображений с учетом квантования яркости при записи в BMP файл
А. Ю. Зражевский, А. В. Кокошкин, В. А. Коротков
Институт радиотехники и электроники им. В.А. Котельникова РАН, Фрязинский филиал
Получена 22 июня 2013 г.
Аннотация. В работе рассмотрен способ восстановления изображения с учетом шумов, вызванных квантованием яркости, при записи в графический файл.
Ключевые слова: аппаратная функция, радиотепловое изображение, восстановление изображения, шум квантования.
Abstract. The method of image recovering accounting noise due to brightness discretization when saving to graphical file is considered.
Key words: point spread function, radio thermal image, image recovering, noise, descretisation.
Одним из источников шумов, мешающих восстановлению изображений, является шум, вызванный квантованием яркости изображения при записи в графический файл. В [6] ранее описывался способ учета в том числе и этого типа шума при использовании инверсной фильтрации с помощью метода опорного изображения [2,4,5]. Однако, если этот тип шума является доминирующим, то возможен более простой способ учета этого шума.
В спектральном виде формирование спектра изображения происходит согласно формуле:
где 
и 
соответствуют
пространственным спектрам соответственно изображения и объекта, а 
- спектр аппаратной функции. В силу того,
что оптическая система имеет конечную апертуру, отличен
от нуля только в определенной области малых пространственных частот. Поэтому
формирование изображения соответствует случаю низкочастотной фильтрации
исходного сигнала. Уменьшению размеров области пропускания оптической системой
способствуют как несовершенство самой оптической системы, так и условия
формирования и фиксации изображения. Например, если имеет
вид функции Гаусса, то спектр в значительной мере
будет определяться именно видом и будет похож на
функцию Гаусса
где 
- среднеквадратичное отклонение.
В качестве примера возьмем изображение, представленное на рис. 1.
Рис.1. Исходное изображение – а и его спектр – б.
После фильтрации (1) при S=4 и дискретизации на 256 уровней яркости (операция записи в файл BMP и чтения из него) получаем изображение объекта и его пространственный амплитудный спектр, представленные на рис. 2.
а б
Рис.2. Расфокусированное изображение – а и его спектр - б.
Для простоты и наглядности, логарифмы амплитуд спектров представим в одномерном виде, взяв значения только вдоль одной диагонали матрицы амплитудного спектра.
Рис.3. Графики логарифма амплитудного спектра вдоль диагонали.
Красный цвет соответствует спектру отфильтрованного изображения, синий – спектру исходного изображения.
На Рис.3 видно, что характер спектров различный. Исходный спектр, за исключением области вблизи нуля, в среднем медленно убывает с отклонением частоты от нуля. Такое поведение спектра на высоких частотах отфильтрованного изображения напоминает кривую Гаусса. Особенно хорошо это заметно на Рис.4, где спектр отфильтрованного изображения показан в сравнении со спектром аппаратной функции.
Рис.4. Графики логарифма амплитудного спектра вдоль диагонали.
Красный цвет соответствует спектру
отфильтрованного изображения, синий – спектр аппаратной функции , имеющей в данном случае вид функции
Гаусса.
На рис.5 представлены амплитудные спектры отфильтрованного изображения до и после дискретизации в 256 уровней.
Рис.5. Графики логарифма амплитудного спектра вдоль диагонали.
Красный цвет соответствует спектру отфильтрованного изображения, синий – спектру изображения после дискретизации в 256 уровней.
Из Рис.5 следует, что дискретизация приводит к искажению спектра за счет замены амплитуды высоких частот высокочастотным шумом.
В силу того, что запись в BMP файл и чтение из него соответствует дискретизации в сигнал с 256 уровнями яркости, сигнал после чтения из файла можно попытаться скорректировать следующим образом. Можно приравнять все спектральные компоненты нулю, если их амплитуда меньше некоторого уровня, величина которого зависит от размерности изображения и числа уровней дискретизации (в нашем конкретном случае, когда изображение имеет размеры 256х256 и 256 уровней яркости, этот уровень равен 2/N, N=256). Если количество уровней дискретизации Nu равно максимальной яркости, то этот уровень практически не зависит от Nu. При этом предполагалось, что вычисление спектра производится по формуле:
Такой подход позволяет после
его применения для восстановления исходного сигнала сразу использовать
инверсную фильтрацию, следующую из (1), что позволяет в пределах полосы
пропускания восстановить исходный сигнал – Рис.6-7.
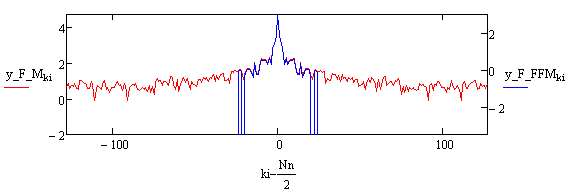
Рис.6. Графики логарифма амплитудного спектра вдоль диагонали.
Красный цвет соответствует спектру исходного изображения, синий – спектру восстановленного изображения.
а б
Рис.7. Восстановленное изображение – а
и отфильтрованное изображение – б. S=4
Подобный подход целесообразно использовать и в том случае, когда в качестве квантования изображения при записи в графический файл выступает ошибка измерения яркости.
Выводы
Таким образом, использование в качестве априорной информации предположение о характере доминирующего шума, вызванного квантованием яркости изображения при записи в графический файл, позволяет правильно выделить область, содержащую этот шум и качественно с помощью инверсной фильтрации восстановить изображение.
1. Р. Гонсалес, Р. Вудс. Цифровая обработка изображений. М. «Техносфера» , 2005, 1071 стр.
2. Зражевский А.Ю., Кокошкин А.В., Новичихин Е.П., Титов С.В., «Повышение качества радиоизображений». «Нелинейный Мир», № 9, 2010г., с. 582-590.
3. Тихонов А.Н., Арсенин В.Я. - Методы решения некорректных задач. М.Наука, 1979
4. Зражевский А.Ю., Кокошкин А.В. Влияние уровня боковых лепестков аппаратной функции на качество восстановленного изображения. «Журнал Радиоэлектроники», №4, 2013 г. http://jre.cplire.ru/jre/apr13/8/text.html
5. Зражевский А. Ю., Коротков В.А. Восстановление искаженного оптической системой радиоизображения с помощью метода опорного изображения. Сб. Тезисы докладов IХ Всероссийский семинар по радиофизике миллиметровых и субмиллиметровых волн. С.122. Нижний Новгород. 2013.
6. Зражевский А. Ю., Коротков В. А. Исследование восстановления сигнала, прошедшего через неидеальный фильтр низких частот. «Журнал Радиоэлектроники», №4, 2013г. http://jre.cplire.ru/jre/apr13/4/text.html
7. Зражевский А. Ю., Коротков В. А. Особенности восстановления искаженного оптической системой радиоизображения с помощью метода опорного изображения. «Журнал Радиоэлектроники», №4, 2013г. http://jre.cplire.ru/jre/apr13/3/text.html