АНАЛИЗ ВЛАГОСОДЕРЖАНИЯ АТМОСФЕРЫ ПО ДАННЫМ ПРИЕМНИКОВ GPS

 

В. Е. Куницын ^1,2, И. А. Нестеров ¹, Н. А. Терешин ¹

¹ Московский Государственный Университет имени М.В. Ломоносова

² Институт физики Земли им. О.Ю.Шмидта РАН

 

Статья получена 8 июня 2015 г.

 

Аннотация. Система GPS с использованием сетей двухчастотных приемников активно применяется в последние годы в задачах зондирования ионосферы и тропосферы. Особый интерес представляет оценка атмосферного влагосодержания, которое важно для улучшения численных прогнозов погоды. В данной работе описывается метод, позволяющий оценивать значение интегрального влагосодержания атмосферы по измеряемым фазовым задержкам сигнала спутников GPS. Производится демонстрация результатов работы метода с использованием данных североамериканской сети GPS-приемников SOPAC. Точность работы метода оценивается путем сравнения результатов с данными из глобального и регионального реанализов погоды.

Ключевые слова: дистанционное зондирование, спутниковые навигационные системы, GPS, влагосодержание,  тропосфера.

Abstract. GPS system has proved itself to be an excellent tool for ionosphere sounding problems. This led to evaluating the feasibility of using dual-frequency GPS-receivers for remote sensing of the troposphere. Sensing water vapour content is of particular interest to research concerned with improving numeric weather forecasts. This article describes a method of measuring integrated water vapour content in the atmosphere by using signal phase delay data from GPS receivers. Sample output is displayed, using SOPAC receiver array data as input. Data from global and regional reanalyses is used to provide comparison and perform error estimation.

Keywords: remote sensing, satellite navigation systems, GPS, precipitable water, troposphere.

 

Введение

Использование GPS для зондирования атмосферы является актуальной областью исследований в физике атмосферы — GPS-метеорологией. Спутники позиционирования делают возможным прецизионное измерение задержек спутникового сигнала в сантиметровом диапазоне длин волн. Это, в свою очередь, позволяет оценивать влияние различных атмосферных компонент на распространение радиоволн.

В частности, в настоящее время хорошо исследованы методы зондирования ионосферы [1]. Они преимущественно основаны на использовании фазовой задержки сигнала на частотах L1 и L2 (1575,42 и 1227,60 МГц). Использование нескольких частот позволяет выделить часть задержки, создаваемую ионосферой, так как она существенно зависит от частоты.

Исследование нейтральной части атмосферы подобным образом затруднено в связи с тем, что остальные компоненты атмосферы, в отличие от ионосферы, не обладают резко выраженными диспергирующими свойствами в сантиметровом диапазоне и не могут быть отделены друг от друга построением разностной комбинации сигналов на нескольких частотах.

Существует ряд работ, которые посвящены применению томографического [2] и радиозатменного [3] подходов к задаче определения атмосферного влагосодержания по данным приемников GPS. Данная статья посвящена рассмотрению более простого метода, который позволяет определять интегральную величину влагосодержания.

1. Тропосферная задержка

Измеряемая приемником GPS фазовая задержка является интегралом фазового показателя преломления и содержит в себе информацию о влиянии различных атмосферных составляющих [4]:

где n_ph — фазовый показатель преломления, описывающий вклад как ионосферы, так и нейтральной атмосферы. Также фазовую задержку можно представить покомпонентно, с учетом возникающих ошибок измерений [5]:

где  — фазовая константа,  — расстояние от спутника до приемника, I — ионосферная задержка, STD (slant tropospheric delay) — тропосферная задержка вдоль луча (вызванная нейтральной атмосферой),  — дополнительные поправки к расстоянию, связанные с позиционированием,  — ошибки часов приемника и спутника соответственно,  — релятивистская поправка ко времени,  — различные приборные шумы.

Тропосферная задержка создается как сухой атмосферой, так и вкладом искомого влагосодержания (как создаваемого паром, так и облаками [6]). Для расчета влагосодержания требуется сначала получить значения тропосферной задержки путем устранения остальных компонент фазовой задержки.

2. Исключение расстояния до спутника и погрешностей позиционирования

Поскольку геометрическое расстояние до спутника является основной компонентой фазовой задержки, в первую очередь требуется точный учет позиций спутников и приемников в моменты отправки и приема сигнала для расчета расстояния между ними.  Такие факторы, как вращение Земли и вращение спутников вокруг нее, дают существенный вклад в расчет геометрического расстояния. Также свой вклад дает релятивистская поправка ко времени , вызванная замедлением времени на Земле согласно ОТО [7], которая частично корректируется часами GPS.

Дополнительным препятствием является то, что хотя координаты спутников известны достаточно точно (среднее отклонение расчетных траекторий от истинных положений не превышает 5-10 см, в зависимости от использованных данных), положение приемников дано в архивах данных GPS лишь приблизительно, и в контексте задачи необходимо ввести дополнительную поправку на положение приемника (которая составляет до нескольких десятков метров).

Помимо этого, необходимо учесть деформации Земли под действием приливных сил. Смещение поверхности Земли достигает величин порядка нескольких десятков сантиметров и имеет циклический характер. Для устранения этого фактора используется упрощенная модель твердых приливов IERS [8].

Также дает свой вклад смещение и вариация фазовых центров антенн в зависимости от угла подъема спутника. В зависимости от рассматриваемой антенны, величины поправок на положение фазового центра антенны могут достигать порядка 1-2 метров для спутников или нескольких десятков сантиметров для приемников. Калибровочные измерения фазовых центров антенн производятся IGS и находятся в открытом доступе [9], что позволяет произвести априорную коррекцию измерений.

3. Разностные комбинации

Для исключения из расчетов неизвестных компонент задержки (фазовая константа, ионосферная задержка) можно использовать комбинации нескольких фазовых измерений.

В первую очередь, использование фазовых измерений одного приемника на нескольких частотах (L1 и L2) позволяет исключить влияния ионосферы с порядками по частоте , оставляя лишь малозначимые члены более высоких степеней частоты (так называемая безионосферная линейная комбинация):

Далее, использование разности нескольких последовательных измерений во времени позволяет исключить фазовую константу (аналогично операции дифференцирования по времени):

В приложении к ошибкам часов приемника можно проделать аналогичнуое действие: если имеются измерения двух приемников A и B, которые принимают сигнал со спутников 1 и 2 (фазовые измерения Ф^А,1, Ф^А,2, Ф^B,1, Ф^B,2), то можно построить следующие разностные операторы:

Применение первого оператора дает величину, не зависящую от ошибки часов приемника А (), второго — исключает ошибку часов спутника 1 (). В силу их линейности, все разностные комбинации 3-6 можно использовать последовательно в любом порядке, исключая все 4 неизвестных величины.  Одновременное взятие разностей между приемниками и между спутниками называется методом двойных разностей [10].

4. Расчет зенитной задержки

В приближении сферически-слоистой атмосферы можно сделать переход от наклонной тропосферной задержки к зенитной тропосферной задержке ZTD (zenith tropospheric delay) с использованием картирующей функции , которая зависит от угла подъема спутника:

в данной работе используется картирующая функция Нила [11], часто используемая в радиоастрономии.

Учитывая наличие неизвестных координат положения приемника (см. раздел 1), и используя введенные разностные комбинации (раздел 3) можно поставить задачу для нахождения функции зенитной тропосферной задержки ZTD, зависящей от времени, и поправки к координатам приемника :

( - вектор направления распространения сигнала). Оставшаяся поправка к времени спутника  является стандартным продуктом служб GPS и может быть взята из архива IGS. Такая постановка является схожей с задачей презиционного точечного позиционирования (PPP, precise point positioning) [12].

Для решения задачи 8 в данной работе используется разложение по кубическим B-сплайнам с тихоновской регуляризацией [13].

5. Получение интегрального влагосодержания

Получаемая решением поставленной задачи зенитная тропосферная задержка, как было сказано ранее, является суммой двух различных компонент: вклада сухого воздуха и вклада влажного воздуха (т. е. влагосодержания). Это можно представить следующим образом:

где ZHD (zenith hydrostatic delay) — зенитная сухая (гидростатическая) задержка, которая зависит от парциального давления сухого воздуха  и температуры и температуры T [4]:

ZWD (zenith wet delay) — зенитная влажная задержка, которая зависит похожим образом от парциального давления водяного пара :

Т. к. первый член является по порядку величины существенно меньше [14] второго, им можно пренебречь. Искомое интегральное влагосодержание IWV (integrated water vapour) является интегралом по высоте от плотности пара  (т. е. зависит от давления пара и температуры):

Зенитная влажная задержка и интегральное влагосодержание связаны следующей зависимостью [14]:

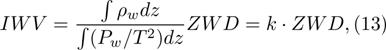
Чтобы вычислить значение зенитной влажной задержки (и, используя соотношение 13, оценить интегральное влагосодержание), нужно оценить значение сухой зенитной задержки. Для этого в данной работе была использована тропосферная модель Саастамойнена [15], аппроксимирующая ее значение с использованием известного приземного давления и температуры.

6. Результаты

Метод был опробован на архиве данных североамериканской сети приемников SOPAC (Scripps Orbit and Permanent Array Center) за 2014 год. Сеть SOPAC покрывает большую часть западного побережья Северной Америки, и является одной из крупнейших сетей приемников в настоящее время.

 

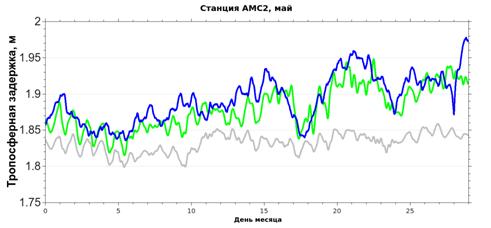
Рис. 1. Ряд рассчитанной тропосферной задержки для станции AMC2 за апрель 2014 г. (сверху) и май 2014 г. (снизу). Модель: оценка тропосферной задержки по данным реанализа с использованием модели Саастамойнена. Расчет: результат работы предложенного метода.

Результаты обработки данных были сравнены, в первую очередь, с рассчитанной по модели Саастамойнена тропосферной задержкой (в том числе с учетом влажной задержки). Параметры для модели Саастамойнена были взяты из реанализа NARR (North American Regional Reanalysis). В качестве примера на рис. 1 приведен пример полученных результатов для одной из станций (имя маркера AMC2). Рис. 1 показывает хорошее количественное соответствие получаемых результатов с моделируемой величиной: среднее отклонение рассчитанной тропосферной задержки от модели составляет 3.2 см, с коэффициентом корреляции 80%.

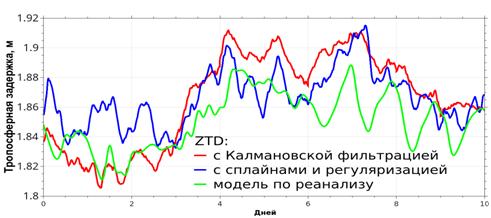
Рис. 2. Сравнение рассчитанной тропосферной задержки с расчетами UNAVCO, и оценкой тропосферной задержки по модели Саастамойнена.

Также было проведено сравнение результатов работы предложенного метода с результатами метода, используемого консорциумом UNAVCO для расчета тропосферной задержки и включающего в себя калмановскую фильтрацию данных. На рис. 2 показано сравнение всех трех указанных величин. Средние отклонения от смоделированной задержки составляют 3.6 см для предложенного метода и 3.1 см для метода UNAVCO. Результаты обоих методов в среднем отличаются друг от друга на 2.1 см. Это не дает возможности судить о том, какой из методов является более эффективным. Преимуществом данного метода, однако, является возможность его обобщения на задачу томографии водяного пара, так как сплайновое разложение искомых функций можно эффективно обобщить на многомерную исследуемую область, в то время как фильтр Калмана не столь удобен в использовании для многомерных задач.

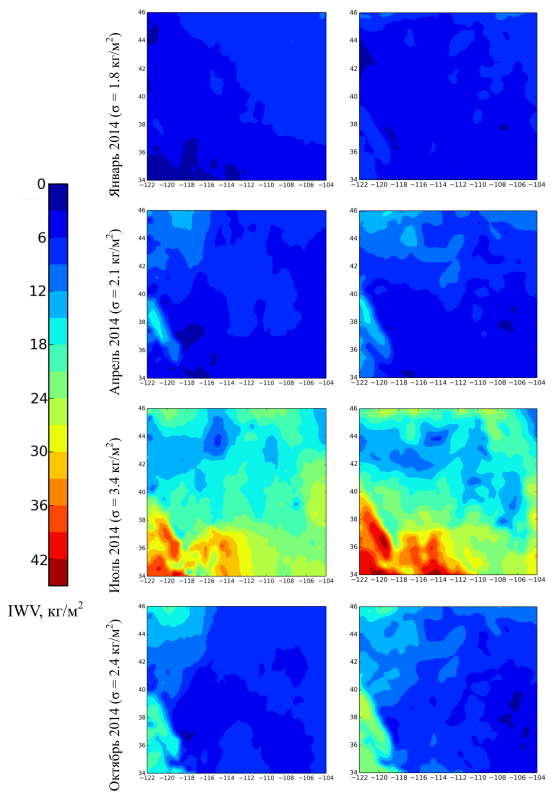
Рис. 3. Сравнение результатов работы метода (слева) с данными реанализа NARR (справа) для различных сезонов (среднемесячные значения).

По построенным временным рядам для каждого приемника были рассчитаны значения интегрального влагосодержания, которые затем были интерполированы на координатную сетку.  На рис. 3 показаны примеры среднемесячных значений получаемых полей интегрального влагосодержания для различных сезонов. Они сравнены с аналогичными полями интегрального влагосодержания, взятыми напрямую из реанализа NARR. Можно наблюдать хорошее качественное совпадение крупномасштабных особенностей изображения. Среднее отклонение влагосодержания составляет порядка 1.7 кг/м² (~30%) в сухие сезоны, и достигает 3.7 кг/м² (~18%) в влажные.

7. Выводы

Разработанный метод позволяет оценивать среднее распределение влагосодержания в исследуемой области с точностью до 3.7 кг/м² (18%). Остаются невыясненными возможности данного метода по разрешению явлений переноса влаги, что является важным для задач уточнения численных прогнозов погоды.

Преимуществом получаемых этим методом результатов является значительно более высокое разрешение по сравнению измерения радиометров, а также хорошее покрытие поверхности суши (в отличие от радиометров, проводящих измерения преимущественно над поверхностью океана). Развитие сетей GPS-приемников позволит использовать этот метод и в других регионах.

Предложенный подход, основанный на сплайновых разложениях с тихоновской регуляризацией, в дальнейшем может быть обобщен для задач многомерной томографии водяного пара в атмосфере [16].

7. Благодарности

Авторы благодарны архиву IGS за предоставление GPS-данных, использованных в работе, и агентству NOAA, предоставляющему доступ к данным реанализа NARR высокого разрешения.

Работа выполнена при финансовой поддержке Российского Научного Фонда (14-17-00637).

Литература

1.       В. Е. Куницын, Е. Д. Терещенко, Е. С. Андреева, Радиотомография ионосферы. М.: Физматлит, 2007.

2.       Bender M. et al. Development of a GNSS water vapour tomography system using algebraic reconstruction techniques //Advances in Space Research. – 2011. – Т. 47. – №. 10. – С. 1704-1720.

3.       Liou Y. A. (ed.). Radio occultation method for remote sensing of the atmosphere and ionosphere. – InTech, 2010.

4.       Solheim F. S. et al. Propagation delays induced in GPS signals by dry air, water vapor, hydrometeors, and other particulates // Journal of Geophysical Research: Atmospheres. – 1999. – Т. 104. – №. D8. – С. 9663-9670.

5.       Kaplan E., Hegarty C. (ed.). Understanding GPS: principles and applications. – Artech house, 2005.

6.       Р. А. Эминов, Э. И. Магеррамов, К вопросу о GPS измерениях общего количестве осаждаемой воды. // Журнал радиоэлектроники: электронный журнал. – 2012. – №7. URL: http://jre.cplire.ru/iso/jul12/8/text.pdf

7.       Ashby N. Relativity in the global positioning system // Living Rev. Relativity. – 2003. – Т. 6. – №. 1.

8.       Scherneck H. G. A parametrized solid earth tide model and ocean tide loading effects for global geodetic baseline measurements // Geophysical Journal International. – 1991. – Т. 106. – №. 3. – С. 677-694.

9.       Rothacher M., Schmid R. ANTEX: The antenna exchange format version 1.3. Format specifications, IGS Central Bureau, Pasadena. – 2006.

10.  Alber C. et al. Obtaining single path phase delays from GPS double differences // Geophysical Research Letters. – 2000. – Т. 27. – №. 17. – С. 2661-2664.

11.  Niell A. E. Global mapping functions for the atmosphere delay at radio wavelengths // Journal of Geophysical Research: Solid Earth. – 1996. – Т. 101. – №. B2. – С. 3227-3246.

12.  Kouba J., Héroux P. Precise point positioning using IGS orbit and clock products // GPS solutions. – 2001. – Т. 5. – №. 2. – С. 12-28.

13.  Eubank R. L. Spline Smoothing and Nonparametric Regression. – 1988.

14.  Bevis M. et al. GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System // Journal of Geophysical Research: Atmospheres. – 1992. – Т. 97. – №. D14. – С. 15787-15801.

15.  Saastamoinen J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites //The use of artificial satellites for geodesy. – 1972. – С. 247‑251.

16.  Troller M. et al. 3‐D refractivity field from GPS double difference tomography // Geophysical research letters. – 2002. – Т. 29. – №. 24. – С. 2-1-2-4.