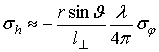УДК 621.396.967
ВЛИЯНИЕ СЖАТИЯ ДАННЫХ НА ОШИБКУ ОПРЕДЕЛЕНИЯ ВЫСОТЫ В РАДИОЛОКАЦИОННОЙ ИНТЕРФЕРОМЕТРИИ РСА КОСМИЧЕСКОГО БАЗИРОВАНИЯ
И. М. Нестеров 1,2, А. Н. Трунов 1,2
1 Московский физико-технический институт (государственный университет)
2 НПП «САИТ»
Статья получена 8 июня 2015 г.
Аннотация. В работе проведено исследование влияния сжатия данных РСА Radarsat различными алгоритмами на ошибку определения высоты в задаче радиолокационной интерферометрии. Введены критерии качества работы алгоритмов сжатия данных РСА. Созданы модели компрессии/декомпрессии данных и получены характеристики алгоритмов блочного адаптивного квантования (БАК) в квадратурном и полярном форматах, векторного квантования (ВК) и вейвлет-преобразования Добеши D4. Получены оценки точности восстановления сжимаемых данных и ошибки определения высоты.
Ключевые слова: сжатие данных РСА, БАК, векторное квантование, вейвлет Добеши D4, радиолокационная интерферометрия.
Abstract. In this paper the impact of SAR raw data compression on the interferometry height accuracy was researched. The performance measures of SAR data compression were introduced. Models of data compression/decompression were created. The performances of BAQ algorithm, BAQ algorithm in data polar format, vector quantization algorithm, wavelet transform D4 algorithm were researched. The estimation of SAR interferometry height accuracy was obtained.
Key words: SAR data compression, BAQ, vector quantization, Daubechies wavelet D4, SAR interferometry.
Введение
В современных радиолокаторах с синтезированной апертурой (РСА) космического базирования поток данных после оцифровки входного сигнала достигает 4 Гбит/с и более, что усложняет процесс дальнейшей обработки, хранения и передачи данных на Землю. Применение алгоритмов сжатия данных, устраняющих избыточность, ведет к уменьшению потока данных с РСА. Алгоритмы сжатия без потерь данных, устраняющие статистическую избыточность, позволяют достигнуть коэффициента сжатия до 1.4 раз. Алгоритмы сжатия с потерями данных устраняют визуальную избыточность и позволяют достигнуть коэффициента сжатия данных до 4 и более раз. В современных РСА применяют алгоритмы с потерями данных. Потери данных оказывают влияние на качество результатов получаемых двумя основными приложениями РСА: синтезом радиолокационных изображений и интерферометрией.
В данной статье рассматривается влияние потерь данных РСА при сжатии на радиолокационную интерферометрию, использующуюся для составления цифровой карты рельефа.
Статистические свойства данных на входе устройства сжатия
Рассмотрим, что представляют собой данные на входе устройства сжатия.
Принимаемый РСА сигнал представляет собой суперпозицию откликов элементарных отражателей [1]:
,
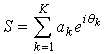(1)
где ak – амплитуды, θk – фазовые задержки. В публикациях [2-3] показано, что амплитуда ak и фаза θk являются статистически независимыми друг от друга и от амплитуд и фаз других элементарных отражателей случайными величинами. В соответствии с центральной предельной теоремой распределение значений принимаемого РСА сигнала – суммы независимых случайных величин – стремится к Гауссовому при K→∞. Мгновенные значения синфазной и квадратурной компонент сигнала S имеют нормальное распределение с нулевым средним. Амплитуды сигнала распределены по Рэлею, фазы – равномерно на интервале [-π, π).
Статистические свойства отсчетов используются алгоритмами сжатия с потерями данных для минимизации ошибки, возникающей в процессе компрессии/декомпрессии.
Критерии качества работы алгоритмов сжатия данных РСА
Для оценки точности восстановления отсчетов исходного сигнала вводятся критерии качества работы алгоритмов сжатия данных РСА.
Приложению синтеза радиолокационных изображений важно как можно более точно восстановить отсчеты сжимаемого сигнала. Критерием качества восстановления сигнала является отношение сигнал/шум квантования [4]:
,
(2)
где 
–
исходный отсчет оцифрованного сигнала, 
-
восстановленный после сжатия отсчет сигнала.
Для приложения радиолокационной интерферометрии важна точность восстановления фазы. В [5] подробно описаны геометрия съемки и процесс построения цифровой карты рельефа, показана зависимость неопределенности высоты от ошибки определения фазы сигнала:
где r – наклонная дальность, 
–
угол наблюдения, отсчитываемый от вертикали, l⊥–
длина проекции линии соединяющей КА на перпендикулярную направлению
сканирования плоскость, λ – длина волны РСА.
Ошибка высоты зависит от точности восстановления фазы, характеризующейся средним фазовым отклонением (СФО) [6]:
,
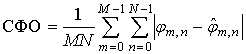(4)
и среднеквадратическим отклонением (СКО) фазы:
,
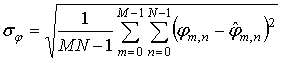(5)
где 
и
- фазы исходного и
восстановленного после сжатия сигнала.
Основной характеристикой работы алгоритма является коэффициент сжатия, представляющий собой отношение количества битов на отсчет до и после сжатия.
Алгоритмы сжатия данных РСА
Для рассмотрения были выбраны алгоритмы, реализующие различные подходы к сжатию данных РСА:
- алгоритм блочного адаптивного квантования (БАК) в тригонометрическом (квадратурном) формате;
- алгоритм БАК в полярном формате;
- алгоритм векторного квантования (ВК);
- алгоритм сжатия на основе вейвлет-преобразования (ВП) D4 (вейвлет Добеши).
В основе алгоритма блочного адаптивного квантования – разбиение потока отсчетов сигнала на блоки, для каждого из которых вычисляются пороговые значения квантователя Макса и производится сжатие [7]. Размеры блока отсчетов выбирают таким образом, чтобы статистика данных была близка к нормальному распределению, но при этом снимаемая сцена была достаточно однородной. Если отсчеты сигнала представлены в виде синфазной и квадратурной компонент, то для вычисления пороговых значений выбирают коэффициенты квантователя Макса для нормального распределения [8]. Если отсчеты представляют собой амплитуду и фазу сигнала, то для амплитуды выбирают коэффициенты Макса соответствующие распределению Рэлея, для фазы – равномерному распределению.
Векторное
квантование происходит в два этапа. На первом этапе составляется кодовая книга
с целью минимизировать ошибку квантования для потока отсчетов. Составление
кодовой книги – итеративный процесс [9]. Каждому элементу тестовой
последовательности ставится в соответствие вектор кодовой книги, для которого
ошибка квантования 
минимальна:
,
(6)
где
– элемент тестовой последовательности,
– вектор кодовой книги. Затем
вычисляются новые значения векторов кодовой книги:
,
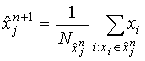(7)
где 
– количество элементов
тестовой последовательности xi,
которые при квантовании становятся вектором 
, n
–
номер итерации. Составление кодовой книги заканчивается, когда приращение суммарной
средней ошибки становится меньше установленного значения ε:
,
(8)
,
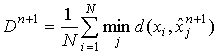(9)
где N – длина тестовой последовательности.
На втором этапе
производится квантование, каждому приходящему отсчету ставится в соответствие
номер вектора в кодовой книге, для которого ошибка квантования минимальна. При восстановлении данных
каждому пришедшему отсчету-номеру ставится в соответствие вектор в кодовой
книге.
Сжатие на основе вейвлет-преобразования Добеши D4.
Вейвлет D4 имеет коэффициенты [10]:
(10)
Вейвлет-преобразование производится для амплитудной компоненты данных, представленных в полярном формате [11]. Вейвлет-преобразование D4 разделяет данные на низкочастотную и высокочастотную составляющие, устраняя одинаковые и линейно растущие компоненты. Преобразование осуществляется путем умножения матрицы преобразования на вектор-столбец отсчетов амплитуд в полярном формате. Матрица преобразования имеет вид:
.
(11)
Прямое вейвлет-преобразование D4:
,
(12)
где
s и 
– вектор-столбец
амплитуд отсчетов до и после вейвлет-преобразования. Компоненты-суммы
вектор-столбца подвергаются вейвлет-преобразованию
до тех пор, пока количество компонент сумм не станет равно двум (меньше
количества коэффициентов D4).
Компоненты-разности нормируются на среднеквадратическое отклонение абсолютных
значений компонент-разностей и квантуются. Обратное вейвлет-преобразование
будет иметь вид:
.
(13)
Моделирование сжатия данных РСА
Для исследования в среде Matlab были созданы модели компрессии/декомпрессии данных РСА. В качестве данных использовались комплексные отсчеты РСА Radarsat с 8-битной синфазной и квадратурной компонентами.
Для моделирования работы устройства сжатия данных алгоритмом БАК с квадратурными компонентами исходный массив комплексных отсчетов разбивался на блоки размером 512 (32х16) отсчетов каждой из квадратур. Методом, описанным в статье [7], производилась оценка СКО квадратурных компонент отсчетов. Значение СКО амплитуд отсчетов i-го блока данных и коэффициенты Макса для нормального распределения использовались при вычислении пороговых значений для квантования отсчетов (i+1)-го блока данных. СКО i-го блока и сжатые данные (i+1)-го блока данных подавались на схему восстановления сжатых данных, где каждому отсчету ставился в соответствие коэффициент Макса для нормального распределения, умноженный на значение СКО.
Результаты моделирования алгоритма БАК с квадратурным форматом отсчетов (БАК кв.) для сжатия данных до 1, 2, 3, 4-битов на отсчет квадратуры (коэффициенты сжатия 8/1, 8/2, 8/3, 8/4) представлены на рисунках 1, 5, 6.
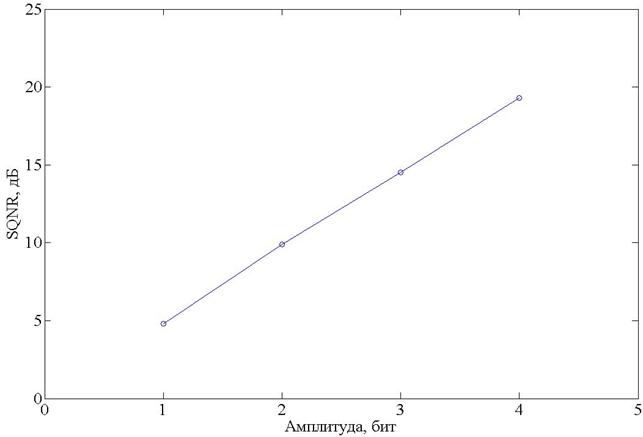
Рисунок 1. SQNR БАК с квадратурным представлением компонент.
При величинах SQNR менее 9-10 дБ на синтезируемом радиолокационном изображении появляются заметные шумовые искажения. Из рисунка 1 видно, что сжатие данных алгоритмом БАК в квадратурном формате до 3-4 битов на отсчет (коэффициенты сжатия 8/3, 2) позволяет получить при синтезе изображение практически неотличимое от оригинального, а при сжатии до 2 битов на отсчет (коэффициент сжатия 4) синтезируемое изображение будет иметь шумовые искажения.
Полученная в результате моделирования информация об искажениях фазы представлена на рисунках 5-6 используется для расчета характерных значений ошибки определения высоты, вносимой алгоритмами сжатия, в задаче радиолокационной интерферометрии.
Для получения полярного формата данных, используя исходные отсчеты квадратурных компонент, были вычислены амплитуда и фаза каждого отсчета:
,
(14)
,
(15)
где Ai, φi – амплитуда и фаза i-го отсчета, round(a) – округленное до ближайшего целого число a, k1 – количество бит в двоичном представлении амплитуды, k2 – количество бит в двоичном представлении фазы, функция arg(a) - вычисляет аргумент комплексного числа ai=Ii+j*Qi на интервале [-π, π).
Для моделирования были выбраны параметры:
k1 = 12, (8 бит – целая часть числа и 4 бита – дробная часть);
k2 = 8, фаза нормируется на π, чтобы значения фазы i-го отсчета были в диапазоне [-1, 1).
Среднеквадратическое отклонение значений амплитуд i-го блока использовалось для вычисления пороговых значений квантователя Макса (распределение Рэлея) и сжатия отсчетов амплитуд (i+1)-го блока данных. Коэффициенты квантователя Макса для равномерного распределения использовались в качестве пороговых значений для нормированных на π фаз комплексных отсчетов. СКО амплитуд i-го блока данных и сжатые данные амплитуд и фаз отсчетов данных (i+1)-го блока данных подавались на схему восстановления данных. Для восстановления амплитуд СКО умножалось на соответствующий отсчету коэффициент Макса для распределения Рэлея. Отсчетам фазы ставился в соответствие коэффициент Макса для равномерного распределения.
Результаты моделирования алгоритма БАК с полярным форматом отсчетов (БАК пл.) для сжатия амплитуды сигнала до 1-4 битов и фазы до 2-5 битов представлены на рисунках 2, 5, 6.
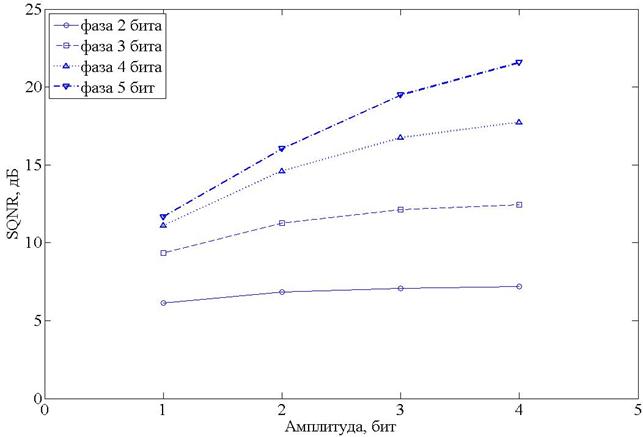
Рисунок 2. SQNR БАК в полярном формате.
Из рисунка 2 видно, что сжатие данных алгоритмом БАК в полярном формате до 2 бит амплитуды и 4 бит фазы (коэффициент сжатия данных 8/3) позволит получить при синтезе изображение с незначительным уровнем шумов, визуально практически неотличимое от оригинального. При использовании меньшего количества бит для представления амплитуды и фазы, на синтезируемом изображении будут наблюдаться шумы и визуальное отличие от исходного.
Сжатие данных алгоритмом БАК в полярном формате при равных коэффициентах сжатия с БАК в квадратурном формате имеет меньшее отношение SQNR на 1-4 дБ, но позволяет точнее восстановить фазу исходного сигнала, что важно для приложения интерферометрии.
В модели векторного квантования для построения кодовой книги в качестве отсчетов тестовой последовательности использовались амплитуды синфазной и квадратурной компонент. Длина тестовой последовательности N = 65536 отсчетов. Минимальная величина приращения ε = 10-3.
Результаты моделирования алгоритма векторного квантования (ВК) для кодовой книги размером 2, 4, 8, 16 векторов (кодируются соответственно 1, 2, 3, 4 битами) представлены на рисунках 3, 5, 6.
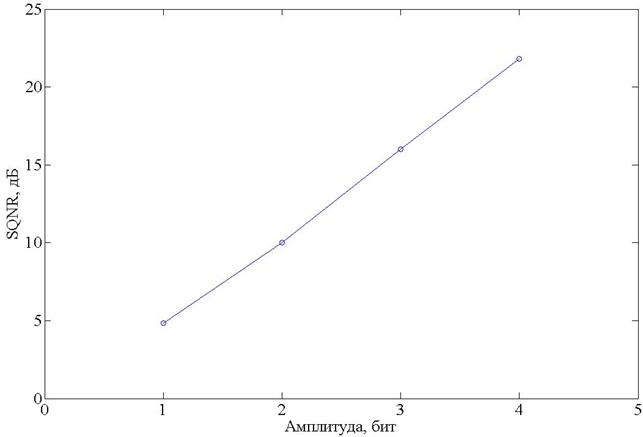
Рисунок 3. SQNR для векторного квантования.
Из рисунка 3 видно, что ВК имеет сравнимые с БАК в квадратурном формате показатели SQNR. Векторное квантование в отличие от БАК имеет более сложную реализацию и требует периодического использования тестовой последовательности для калибровки векторов кодовой книги.
В модели сжатия с использованием вейвлет-преобразования (ВП D4) комплексные данные были приведены к полярному формату. Вейвлет-преобразованию подвергалась амплитуда сигнала. Размер блока отсчетов амплитуд был выбран равным 2048, т.к. после преобразования D4 остается две низкочастотные компоненты размером 12 бит (в других моделях одно СКО на 1048 отсчетов), остальные компоненты нормируется СКО и квантуются.
Результаты моделирования вейвлет-преобразования D4 (ВП D4) для сжатия амплитуды сигнала до 1-4 битов и фазы до 2-5 битов представлены на рисунке 4.
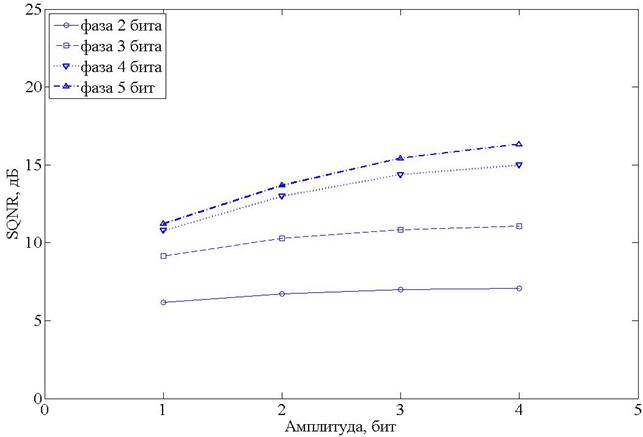
Рисунок 4. SQNR для сжатия на основе вейвлет-преобразования D4.
Из данного рисунка видно, что сжатие на основе вейвлет-преобразования Добеши D4 имеет сравнимые характеристики SQNR c алгоритмом БАК в полярном формате при коэффициентах сжатия 4 и более (1-2 бита на отсчет амплитуды, 2-3 бита на отсчет фазы). При коэффициентах сжатия меньше 4, сжатие ВП D4 имеет SQNR на 2-5 дБ меньше, чем БАК и векторное квантование. Для увеличения SQNR и более точного восстановления значений амплитуд требуются вейвлеты, устраняющие моменты старших порядков, но это усложняет практическую реализацию.
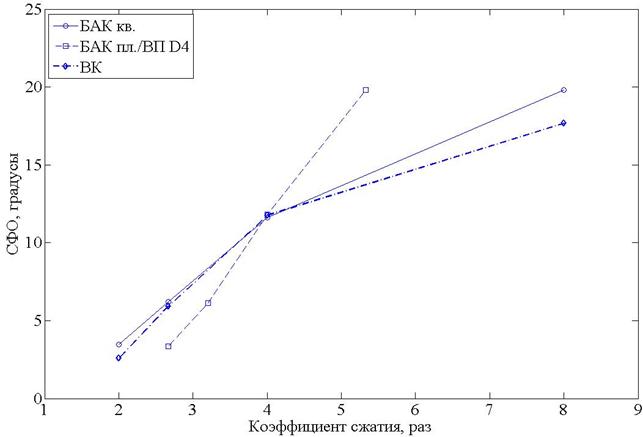
Рисунок 5. СФО для алгоритмов БАК кв., БАК пл., ВК, ВП D4.
На рисунках 5, 6, для алгоритмов БАК в полярном формате (БАК пл.) и вейвлет-преобразования Добеши D4 (ВП D4) показаны характеристики при сжатии амплитудной компоненты до 1 бита на отсчет и сжатии фазы до 2-5 битов на отсчет. Коэффициент сжатия рассчитывался, исходя из 8-битового представления синфазной и квадратурной компонент на входе устройства сжатия.
Из рисунка 5 видно, что при одинаковых коэффициентах сжатия не превышающих 4 раз, преобразование данных к полярному формату позволяет получить СФО на 2-3 градуса меньше, чем при сжатии/восстановлении квадратурных компонент отсчетов. Больший коэффициент сжатия при равных СФО для полярного формата объясняется тем, что амплитуда сжата до 1 бита и больше битов выделено для представления фазы.
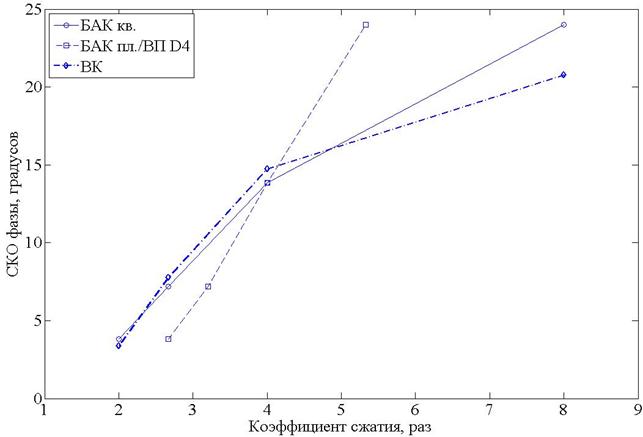
Рисунок 6. СКО фазы для алгоритмов БАК кв., БАК пл., ВК, ВП D4.
Результаты моделирования, представленные на рисунке 6, показывают, что при коэффициентах сжатия не превышающих 4 раз векторное квантование имеет на 1 градус меньшее СКО фазы, чем сжатие алгоритмом БАК с квадратурным представлением отсчетов, а выделение фазовой компоненты в полярном формате позволяет работать с большими коэффициентами сжатия.
Полученные в результате моделирования характеристики восстановления фазы при компрессии/декомпрессии данных используем для оценки точности определения высоты в задаче радиолокационной интерферометрии.
Влияние сжатия на радиолокационную интерферометрию
Для космического аппарата Radarsat [12], данные которого были подвергнуты компрессии/декомпрессии, характерные значения орбитальных параметров:
.
Вычисленные по формуле (3) характерные значения ошибки определения высоты в задаче интерферометрии вследствие сжатия данных приведены в таблице 1.
Таблица 1. Характеристики алгоритмов сжатия данных РСА.
|
Алгоритм |
Коэффициент сжатия |
SQNR, дБ |
СФО, градусов |
σφ, градусов |
σh, метров |
|
БАК квадр. 1I+1Q |
8 |
4.8 |
19.8 |
24.0 |
6.1 |
|
БАК квадр. 2I+2Q |
4 |
9.9 |
11.6 |
15.7 |
4.0 |
|
БАК квадр. 3I+3Q |
8/3 |
14.5 |
6.2 |
9.0 |
2.3 |
|
БАК квадр. 4I+4Q |
2 |
19.3 |
3.5 |
5.1 |
1.3 |
|
БАК поляр. 1А+2Ф |
16/3 |
6.1 |
19.8 |
24.0 |
6.1 |
|
БАК поляр. 1А+3Ф |
4 |
9.4 |
11.8 |
13.8 |
3.5 |
|
БАК поляр. 1А+4Ф |
16/5 |
11.1 |
6.1 |
7.2 |
1.8 |
|
БАК поляр. 1А+5Ф |
8/3 |
11.7 |
3.3 |
3.8 |
1.0 |
|
ВК 1I+1Q |
8 |
4.8 |
17.7 |
20.8 |
5.3 |
|
ВК 2I+2Q |
4 |
10.0 |
11.8 |
14.7 |
3.8 |
|
ВК 3I+3Q |
8/3 |
16.0 |
6.0 |
7.8 |
2.0 |
|
ВК 4I+4Q |
2 |
21.8 |
2.6 |
3.4 |
0.9 |
|
D4 1А+2Ф |
16/3 |
6.2 |
19.8 |
24.0 |
6.1 |
|
D4 1A+3Ф |
4 |
9.2 |
11.8 |
13.8 |
3.5 |
|
D4 1A+4Ф |
16/5 |
10.8 |
6.1 |
7.2 |
1.8 |
|
D4 1А+5Ф |
8/3 |
11.2 |
3.3 |
3.8 |
1.0 |
При сжатии данных алгоритмом БАК в полярном формате с квантованием фазы 5 битами, вейвлет-преобразованием D4 с квантованием фазы 5 битами, ВК с квантованием каждой квадратуры 4 битами ошибка определения высоты в задаче радиолокационной интерферометрии не превосходит 1 м. При этом алгоритмы БАК в полярном формате и вейвлет-преобразования D4 имеют коэффициент сжатия 8/3 (1 бит амплитуда и 5 бит фаза), ВК – коэффициента сжатия 2 (4 бита на квадратуру). Если данные используются также для синтеза радиолокационных изображений, то при коэффициенте сжатия 2, векторное квантование обеспечивает отношение сигнал/шум квантования 21.8 дБ, БАК в полярном формате 19.5 дБ, БАК в тригонометрическом формате 19.3 дБ (с ошибкой высоты порядка 1.3 метров), вейвлет-преобразование D4 15.4 дБ.
Заключение
В данной работе было проведено исследование влияния сжатия данных в РСА космического базирования на ошибку высоты в задаче радиолокационной интерферометрии.
В работе введены критерии качества работы алгоритмов сжатия данных, позволяющие оценить точность восстановления данных после сжатия, относительно исходных данных: отношение сигнал/шум квантования (SQNR), среднее фазовое отклонение (СФО), среднеквадратическое отклонение фазы (СКО фазы).
Описаны подходы к реализации моделей компрессии/декомпрессии данных на основе алгоритмов блочного адаптивного квантования (БАК) в квадратурном формате, БАК в полярном формате, векторного квантования (ВК), вейвлет-преобразования Добеши D4 (ВП D4).
В статье приведены полученные с помощью моделирования характеристики алгоритмов сжатия, позволяющие оценить возможность применения рассмотренных алгоритмов с соответствующими параметрами в задачах синтеза радиолокационных изображении и радиолокационной интерферометрии.
Результаты моделирования и проведенный расчет характерной ошибки определения высоты в задаче радиолокационной интерферометрии показывают, что выделение из сигнала фазовой компоненты (БАК в полярном формате и Вейвлет-преобразование D4) и отдельное её сжатие позволяет достигнуть больших коэффициентов сжатия при сравнимых ошибках определения высоты, чем в случае сжатия квадратурных компонент (БАК в квадратурном формате и ВК). Если при этом стоит задача синтеза радиолокационных изображений, то ВК и БАК (в обоих форматах) обеспечивают лучшее качество.
Рассмотренные алгоритмы могут быть реализованы на практике в составе бортового устройства сжатия данных РСА космического аппарата.
Литература
1. A. El Boustuni, K. Brunham, W. Kinsner. A review of current raw SAR data compression techniques // IEEE TRANSACTIONS ON GEOSCIENCE AND REMOTE SENSING, VOL. 36, NO. 2, MARCH 1998 – pp.925-930
2. D. Lebedeff, P. Mathieu, M. Barlaud, C. Lambert-Nebout, P. Bellemain. Adaptive vector quantization for raw SAR data // Acoustics, Speech, and Signal Processing, ICASSP-95, vol.4, 1995 – pp. 2511-2514
3. Б.Р. Левин. Теоретические основы радиотехники. М.: Радио и связь, 1989 – С.69-77
4. U. Benz, K. Strodl, A. Moreira. A comparison of several algorithms for SAR raw data compression // IEEE TRANSACTIONS ON GEOSCIENCE AND REMOTE SENSING, VOL. 33, NO. 5, SEPTEMBER 1995 – pp.1266-1276
5. G. Franceschetti, R. Lanari. Synthetic aperture radar processing– Boca Raton: CRC Press, 1994. – pp.167-171
6. N. Agrawal, K. Venugopalan. SAR signal processing algorithm // ARPN Journal of Engineering and Applied Sciences, VOL. 4, NO. 9, NOVEMBER 2009 – pp.40-45
7. R. Kwok, W. Johnson. Block Adaptive Quantization of Magellan SAR Data // IEEE TRANSACTIONS ON GEOSCIENCE AND REMOTE SENSING, VOL. 27, NO. 4, JULY 1989 – pp.375-383
8. J. Max. Quantizing for minimum distortion // Information Theory, IRE Transactions on, VOL. 6, March 1960 – pp.7-12
9. Y. Linde, A. Buzo, R.M. Gray. An algorithm for vector quantizer design // IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. COM-28, NO. 1, JANUARY 1980 – pp.84-95
10. I. Daubechies. “Ten lectures on wavelets“, SIAM, Pennsylvania, Philadelphia, USA 1992.
11. M. Brandfass, W. Coster, U. Benz, A. Moreira. Wavelet based approaches for efficient compression of complex SAR image data // Geoscience and Remote Sensing, 1997. IGARSS '97. VOL. 4, 1997 – pp. 2024-2027
12. Canadian Space Agency [электронный ресурс ]. URL: http://www.asc-csa.gc.ca/eng/satellites/radarsat1/components.asp