"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 3 , 2000

оглавление

дискуссия

МЕТОДЫ ЦИФРОВОГО МОДЕЛИРОВАНИЯ РАДИОЛОКАЦИОННЫХ ХАРАКТЕРИСТИК СЛОЖНЫХ ОБЪЕКТОВ НА ФОНЕ ПРИРОДНЫХ И АНТРОПОГЕННЫХ ОБРАЗОВАНИЙ

А.Б.Борзов*, А.В.Соколов**, В.Б. Сучков*

* - Московский Государственный технический университет им. Н.Э. Баумана,
**- Институт радиотехники и электроники РАН

Рассматриваются общие принципы методики синтеза отражательных характеристик сложных радиолокационных целей в коротковолновом диапазоне длин волн. Показано значение существующих на сегодняшний день программных и вычислительных средств при разработке геометрических моделей сложных радиолокационных целей и разновидностей фоновых образований. Приведены расчетные характеристики рассеяния типовых радиолокационных объектов, полученные с использованием современных средств и методов объектно-ориентированного программирования.

Структура "точка" описывает геометрический примитив, представляющий точку принадлежащую поверхности объекта и, кроме того, являющуюся вершиной плоского треугольного элемента. Внутренними данными этой структуры являются три координаты точки в мировой системе координат, представленной на рис. 2. Массив экземпляров этой представляет собой единый список всех точек (вершин) объектов радиолокационной сцены.

Рис. 2. Система координат радиолокационной сцены.

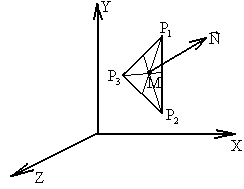
Рис. 3. Треугольная пластина в системе координат сцены.

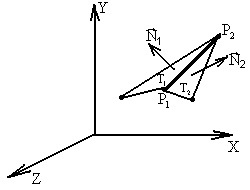
Рис. 4. Плоское ребро в системе координат сцены.

Структура "треугольник" описывает плоскую треугольную пластину, вершины которой лежат на поверхности объекта. Элементами этой структуры являются номера трех вершин треугольника p1, p2 и p3 (рис. 3) в списке всех точек модели (в массиве экземпляров структур "точка"). Другими внутренними данными структуры "треугольник" являются индекс элемента сцены, к которому принадлежит данный треугольник и индекс, определяющий уникальный набор электрофизических свойств треугольника. Инициализация этих индексов для каждого треугольника модели осуществляется в процессе конвертации текстового формата данных в цифровой. Средняя точка треугольника (рис. 3) является экземпляром структуры "точка" и образуется пересечением всех трех медиан треугольника. В дальнейших расчетах средняя точка служит началом локальной системы координат треугольника. Элементом структуры является также вектор нормали к плоскости треугольника с вершинами p1, p2, p3, имеющий координаты в единой системе координат сцены (рис. 3). Еще одним параметром, необходимым в дальнейших расчетах является площадь треугольника. Массив экземпляров структуры "треугольник" образует список всех треугольных пластин образующих поверхности объектов сцены.

Структура "ребро" - описывает прямую линию, соединяющую 2 точки, лежащие на поверхности объекта. Считается, что ребро образовано двумя точками и двумя примыкающими друг к другу треугольниками. Первые два элемента p1 и p2 в рассматриваемой структуре являются номерами двух вершин, лежащих на поверхности объекта и образующих ребро (рис. 4). По аналогии со структурой "треугольник" номера вершин определяются в списке экземпляров структуры "точка". Другими элементами структуры "ребро" являются номера треугольных элементов t1 и t2, образующих ребро в общем списке треугольников модели (массиве экземпляров структуры "треугольник"). Следует отметить, что современные системы САПР конвертируют два типа ребер. Первый тип представляет собой реальные ребра, образуемые в результате действительно имеющего место излома гладкой поверхности объекта. Другой тип ребер образуется в результате наложения плоской треугольной сетки на гладкую поверхность объекта и образования так называемых "мнимых" изломов. Такие ребра называются "мнимыми" ("виртуальными") и при решении радиолокационных задач использоваться не должны. Поэтому общий список ребер модели (экземпляров структур "ребро") должны образовывать только реальные ребра. Таким образом, в результате формирования цифровой геометрической модели сцены образуются три списка экземпляров структур основных геометрических примитивов: точка, треугольник и ребро. Списки экземпляров являются исходными данными при решении радиолокационных задач.

Возможности предлагаемой технологии позволяют моделировать радиолокационные характеристики сложных объектов на разных участках траектории движения носителя РЛС. При этом используется дискретное представление траектории движения в виде совокупности отдельных положений РЛС в пространстве относительно сложного объекта. Каждое положение РЛС характеризуется координатами фазового центра антенной системы в системе координат сцены (рис. 5), вектором , характеризующим направление максимума ДНА, координатами поляризационных ортов системы и вектором скорости носителя РЛС . Для расчета отраженного сигнала на данном участке траектории движения РЛС определяется видимая часть поверхности объекта с заданного ракурса наблюдения. С использованием известных алгоритмов затенения и маскировки элементов сложного объекта из сформированных ранее массивов экземпляров структур треугольников и ребер геометрической модели выбираются номера элементов, видимых РЛС с данного ракурса. Соответственно при расчете отраженного от объекта сигнала используются только видимые в данный момент времени элементы поверхности объекта.

 где - полное поле рассеяния гладкой части объекта, - полное поле рассеяния острых кромок (ребер) модели, - полное поле рассеяния фоновых образований, - полное поле рассеяния, обусловленное взаимными переотражениями волн между отдельными элементами сложных объектов, - полное поле рассеяния, обусловленное взаимными переотражениями волн между элементами сложных объектов и элементами фоновых образований.

Первая компонента в соотношении (1) формируется путем когерентного суммирования полей рассеяния всех плоских треугольных элементов, образующих поверхность сложного объекта и видимых с данного ракурса наблюдения. Как уже отмечалось ранее, в структуру данных треугольного элемента входят три образующие его вершины, средняя точка треугольника, нормаль к его плоскости, площадь треугольника и индекс, определяющий принадлежность к одному из элементов сцены. Для определения локального рассеянного поля треугольного элемента выбирается система координат треугольника в соответствии с рис. 6. Началом локальной системы координат служит средняя точка треугольника. В качестве оси y выбирается нормаль к плоскости треугольника, ось x проводится из средней точки в первую из вершин треугольника, а ось z определяется путем векторного произведения двух векторов. Падающая на треугольник плоская волна характеризуется вектором поляризации и направлением распространения .Направление распространения отраженной волны на приемник с локальным вектором поляризации характеризуется направляющим вектором , который проводится из средней точки треугольника в точку расположения приемной системы. Предполагается, что треугольный элемент обладает вполне определенными электродинамическими свойствами, которые заданы для всего элемента сцены. Треугольный элемент может быть идеально проводящим, диэлектриком, а также обладать многослойным радиопоглощающим покрытием. При этом в качестве электродинамических параметров используется комплексная диэлектрическая проницаемость и магнитная проницаемость . Если на поверхности треугольника имеется многослойное покрытие, то для каждого слоя покрытия толщиной hi назначается соответствующие значения и . В качестве метода расчета поля рассеяния треугольного элемента, принадлежащего гладкой части сложного объекта используется известный метод физической оптики, в основе которого лежит интеграл Стреттона-Чжу. С использованием метода Гордона [1] при решении интеграла физической оптики выражение для рассеянного поля треугольного элемента принимает следующий вид: 

,

(3)

где - значение функций направленности передающей и приемной антенных систем, - амплитуда зондирующего сигнала, - векторный множитель, функционально зависящий от поляризации падающей волны электродинамических параметров треугольника, - вектор, проведенный из средней точки треугольника в одну из его вершин (рис. 6), - проекция вектора на плоскость треугольника, причем , - волновое число падающего излучения, - расстояния от средней точки треугольника до передающей и приемной систем, - векторы скорости носителей передающей и приемной систем.

С учетом того, что вектор поляризации может принимать произвольную ориентацию в поперечной плоскости падающей волны его удобно представить в локальном базисе: , где вектор - принадлежит плоскости падения волны, а - вектор, ортогональный плоскости падения. Подобное представление поляризационного вектора падающей волны позволяет учесть практически все типы поляризации волн (наклонную линейную, круговую, эллиптическую). Используя рассмотренное выражение для поляризационный множитель в (2) удобно представить в виде следующих соотношений:

где - магнитный вектор падающей плоской волны, , - векторы локального базиса падающей волны, - единичный вектор, - угол падения волны на плоскость треугольника.

Соотношения (5) и (6) представляют собой соответственно вертикально и горизонтально поляризованную составляющую электромагнитного поля на поверхности треугольника. При этом определяются как геометрооптические коэффициенты отражения от плоскости треугольника и в случае однородного материала поверхности являются коэффициентами Френеля, зависящими от конкретных значений и . Если на поверхности треугольника имеется многослойное электродинамическое покрытие, то коэффициенты определяются с помощью известных соотношений, приведенных в [4, 5]. Таким образом, расчет поля рассеяния гладкой части возможен для любых типов электродинамических свойств сложного объекта.

Кроме того, следует учесть, что линейный размер каждого треугольного элемента поверхности объекта должен соответствовать критерию дальней зоны, согласно которому . Только в этом случае падающую на треугольник электромагнитную волну можно считать локально плоской. Данное условие позволяет корректно применять соотношение (2) для расчета поля рассеяния треугольного элемента. Для повышения точности расчета интегральных характеристик рассеяния сложного объекта, линейный размер каждого треугольного элемента его поверхности должен быть меньше длины волны падающего излучения. Как правило, при расчете реальных целей используется критерий, согласно которому . Поэтому для сложных объектов, линейные размеры которых в десятки и сотни раз превышают длину волны, общее количество треугольных элементов может достигать сотен тысяч и миллионов единиц. Естественно, что обработка таких объемов данных требует очень больших затрат аппаратных ресурсов и машинного времени.

Расчет второй компоненты результирующего рассеянного поля в соотношении (1) осуществляется путем когерентного суммирования дифракционных полей рассеяния острых кромок (ребер) объекта, видимых РЛС на данном ракурсе наблюдения. Как уже отмечалось, в формировании полного рассеянного поля должны участвовать только реальные ребра, т. е. кромки, образованные действительными изломами гладкой поверхности объекта. Структура данных каждого элементарного ребра образуется из номеров двух треугольников образующих ребро и номеров двух вершин, лежащих на поверхности объекта. Доступ к соответствующим структурам треугольников и точек осуществляется через массивы экземпляров соответствующих структур, образованных на этапе формирования цифровой геометрической модели радиолокационной сцены. При этом ребро считается видимым РЛС, если видимым является хотя бы один из образующих ребро треугольников. Начало локальной системы координат ребра выбирается в одной из его вершин (рис. 7).

Рис. 7. Локальная система координат плоского ребра.

Ось y совпадает с нормалью видимого треугольника, образующего ребро. Ось x проводится через две вершины ребра, а ось z определяется векторным произведением двух векторов. Другие обозначения в данной системе координат аналогичны рис. 6. В локальной системе координат проводится расчет поля рассеяния плоского ребра, являющегося отдельным вкладом в полное рассеянное поле. Для оценки дифракционного поля рассеяния плоского ребра используется метод эквивалентных токов, сущность которого заключается в вычислении неравномерной части тока, текущего вдоль ребра. В результате интегрирования вдоль контура ребра (p1,p2) (рис. 7) длиной L получено следующее выражение для рассеянного поля: 

,

(7)

где , F, G - коэффициенты дифракции соответственно для электрической и магнитной компонент падающего поля, - единичный вектор, совпадающий с осью x, , - углы между направляющими векторами падающей и отраженной волн и осью x соответственно.

Коэффициенты дифракции F и G в соотношении (7) могут определяться по разному в зависимости от условий наблюдения и облучения ребра и его электродинамических параметров. Впервые коэффициенты дифракции идеально проводящего ребра были получены П. Я. Уфимцевым [7] методом физической теории дифракции. Использовать коэффициенты дифракции Уфимцева рационально лишь в случае моностатической локации ребра. При бистатической локации более корректными считаются выражения коэффициентов дифракции в форме Михаэли [2]. Отдельной проблемой является вычисление коэффициентов дифракции для диэлектрического ребра с заданными значениями и , а также ребра с многослойным покрытием. Существующие на сегодняшний день работы отечественных и зарубежных исследователей позволяют решить и эту проблему. При выборе линейного размера плоского ребра действуют те же ограничения, что и для размера треугольного элемента, перечисленные выше. Очевидно, что при дискретизации криволинейных ребер совокупностью локально плоских ребер, длина элементарного ребра не должна превышать половины длины волны .

Для оценки третьей компоненты полного рассеянного поля (1) в настоящее время существует целый ряд моделей применяемых в зависимости от типа фоновых образований, их геометрической формы, происхождения, электродинамических параметров, условий наблюдения и требуемой точности вычислений. Наиболее разработанными считаются методы оценки полей рассеяния статистически шероховатых поверхностей. Их применение в рамках рассматриваемой методики основано на тех же структурах данных геометрической модели, которые применялись для сложных объектов. Как было отмечено ранее, современные САПР позволяют формировать геометрическую модель фонового сюжета по аналогии с поверхностью сложного объекта в виде совокупности плоских треугольных элементов. Основным отличием треугольного элемента, принадлежащего шероховатой поверхности от треугольника гладкой части объекта, состоит в том, что элементарный отражатель шероховатой поверхности кроме электродинамических свойств наделяется вполне определенными статистическими свойствами, характеризующими случайные отклонения поверхности треугольного элемента от плоскости. В качестве таких статистических параметров обычно используют среднеквадратичную высоту неровностей [м] и интервал корреляции высот неровностей [м]. Треугольный элемент, обладающий такими статистическими свойствами с вполне конкретными значениями и , считается элементом шероховатой поверхности. Система координат такого отражателя формируется по аналогии с рис. 6. Дифракционное поле рассеяния шероховатого треугольника носит стохастический характер и в самом общем случае его можно представить в следующем виде:

 где - удельная эффективная площадь рассеяния (ЭПР) отражателя со случайными неровностями, - площадь треугольного элемента, - фаза рассеянного поля, представляющая собой случайную величину, распределенную по равномерному закону .

В зависимости от типа случайных неровностей на поверхности треугольного элемента существует три метода расчета его удельной ЭПР. Для так называемых крупномасштабных неровностей, размеры которых превышают длину волны используется метод касательной плоскости (МКП), а для мелкомасштабных неровностей - метод малых возмущений (ММВ). При наличии на поверхности треугольника неровностей обоих типов используется комбинация методов МКП и ММВ. Полученные с помощью перечисленных методов соотношения для удельных ЭПР имеют следующий вид [4]:

где соответствует методу МКП, соответствует методу ММВ, соответствует методу ММВ, модифицированному на случай двухкомпонентных неровностей, - среднеквадратичный тангенс угла наклона неровностей, - относительная шероховатость мелкомасштабных неровностей, - векторные множители, зависящие от поляризации падающей волны и электродинамики поверхности, приведенные в [3, 4].

Расчет результирующего рассеянного поля радиолокационной сцены (1) осуществляется методом цифрового моделирования и проводится в несколько этапов. На первом этапе разрабатывается модель траектории движения носителя РЛС (рис. 5). На втором этапе осуществляется анализ структур исходных данных цифровой геометрической модели сцены для каждого положения траектории движения РЛС, а также происходит инициализация электродинамических и статистических свойств отдельных элементов сцены. Третий этап характеризуется непосредственным расчетом рассеянного поля. Как было отмечено ранее, полное рассеянное поля определяется путем когерентного суммирования элементарных вкладов всех треугольных элементов сложных объектов и фоновых образований, ребер модели видимых для данного положения РЛС на участке траектории и вкладов переотражений отдельных треугольников. При этом вычисление локальных полей рассеяния перечисленных элементов проводится в рамках разработанной ранее объектно-ориентрованной модели [4,8]. В соответствии с данной моделью методы расчета дифракционного поля каждого типа рассеивающего элемента (треугольник, ребро) представляются в форме объектно-ориентированных классов. Каждый класс содержит приватные данные, представляющие собой параметры данного типа отражателя и методы оценки его поля рассеяния. В соответствии с соотношениями (1-12) формируется пять классов-методов, характеризующих рассеивающие свойства соответственно треугольного элемента гладкой части (2-6), острой кромки (7-8), треугольного элемента с крупномасштабными неровностями (10), с мелкомасштабными неровностями (11) и с двухкомпонентными неровностями (12). Все классы-методы являются наследниками двух базовых классов, в которых формируются вектора базисов падающей и отраженной волн, а также электродинамические параметры элемента сцены в зависимости от длины волны . Объекты базовых классов не создаются, т. к. эти классы являются виртуальными и представляют собой структуры данных, общих для всех классов-методов. Объект класса-метода создается на этапе расчета и представляет собой процесс взаимодействия плоской волны с элементарным отражателем, обладающим определенной совокупностью электродинамических или статистических параметров. Созданный объект класса-метода позволяет вычислить поля рассеяния соответствующего ему элементарного отражателя в процессе суммирования вкладов от всех элементов данного типа. На заключительном этапе расчета происходит анализ и обработка расчетных данных. Если в качестве исходных данных используется сложный зондирующий сигнал, то проводится спектральная обработка рассеянного поля (1). При этом соотношение (1) вычисляется для каждой спектральной составляющей сигнала. В результате представляется возможным получить как спектр отраженного сигнала, так и его временную реализацию. Другим направлением обработки результатов является построение энергетических диаграмм рассеяния сложных целей и анализ этих диаграмм с помощью вероятностных методов. В качестве энергетической характеристики, как правило, используется эффективная площадь рассеяния цели. Кроме того, нетрудно оценить энергетические вклады отдельных элементов сцены в результирующий сигнал.

Оценка возможностей рассматриваемой методики и корректности применения приведенных соотношений для полей рассеяния различных элементов проводится путем вычисления интегральных характеристик рассеяния типовых эталонных отражателей. Для анализа рассевающих свойств гладкой части объектов и ее изломов (первая и вторая компоненты в (1)) рассматриваются три типовых отражателя: сфера, цилиндр и диск. На рис. 8 приведена диаграмма обратного рассеяния идеально проводящей сферы радиуса R=8 см на длине волны см. Поскольку поверхность сферы не имеет изломов, проводился расчет лишь первой компоненты рассеянного поля (1) путем когерентного суммирования вкладов треугольных элементов, размеры которых составляли .

Рис. 8. Диаграмма обратного рассеяния идеально проводящей сферы(штриховая линия - расчет, сплошная линия - теория).

Поле рассеяния треугольного элемента определялось в соответствии с соотношениями (2-6). В качестве теоретического значения ЭПР сферы использовалось соотношение (на рис. 8 - сплошная линия). В соответствии с рис .8, колебания расчетного значения ЭПР сферы (штриховая линия) относительно теоретического значения не превышают 0.002 дБ, что может быть обусловлено лишь погрешностью расчета. Расчет вкладов острых кромок был проведен на примере идеально проводящего цилиндра, схема локации которого приведена на рис. 9.

Рис. 9. Схема радиолокации цилиндра.

Цилиндр облучался плоской волной с длиной см в плоскости XOY (рис. 9) в интервале углов визирования (40-50)° . Расчет ЭПР краевой части тока производился от изломов образующей цилиндра и его оснований. При этом криволинейные ребра представлялись совокупностью плоских ребер, линейный размер которых составлял . Результирующий вклад острых кромок цилиндра (вторая компонента в (1)) определялся когерентным суммированием полей рассеяния локально плоских ребер в соответствии с соотношениями (7-8). На рис. 10-11 приведены зависимости ЭПР цилиндра, представленного на рис. 9, рассчитанной только с учетом краевых токов для E и H поляризаций падающей волны. Штриховой линией обозначена расчетная зависимость, полученная методом цифрового моделирования, а сплошной линией изображена зависимость ЭПР, полученная аналитически с использованием метода физической теории дифракции по соотношениям, приведенным в [7]. Как видно из графиков расчетные и теоретические кривые практически не различаются. Средняя погрешность расчета краевой части тока по сравнением с ФТД составляет не более 5 %.

Рис. 10. Зависимость ЭПР цилиндра (краевая часть) от угла визирования на H-поляризации (штриховая линия - расчет, сплошная линия - теория).

Рис. 11. Зависимость ЭПР цилиндра (краевая часть) от угла визирования на E-поляризации (штриховая линия - расчет, сплошная линия - теория).

Расчет результирующего поля рассеяния (1), т. е. когерентной суммы первой и второй компонент рассмотрим на примере идеально проводящего диска с радиусом R=2.4 см (рис. 12).

Рис. 12. Схема радиолокации диска

Полная ЭПР диска определялась путем совместного учета полей рассеяния треугольных элементов гладкой части и острых кромок. Зависимость ЭПР, представленная на рис. 13 штриховой линией была получена на длине волны см в интервале углов (0-90)° при его локации в плоскости XOY. Вклады треугольных элементов в полное поле вычислялись по соотношениям (2-6) методом физической оптики, а вклады ребер из соотношений (7-8) методом эквивалентных токов. Теоретическая кривая на рис. 13 (сплошная линия) получена с использованием аналитических соотношений Уфимцева [7], представляющих собой комбинацию методов физической оптики (ФО) и ФТД. Как и в случае цилиндра, расчетная ЭПР диска практически не отличается от теоретической, причем погрешность расчета не превышает 4 %.

Рис. 13. Зависимость ЭПР диска (результирующая компонента) от угла визирования (штриховая линия)

В заключении рассмотрим методы вычисления четвертой и пятой компонент полного поля (1), характеризующих вклады переотражений между отдельными элементами сложных объектов и фоновых образований. Данная проблема решается путем комбинированного применения метода геометрической оптики, используемого для построения лучевых трубок и метода физической оптики, позволяющего вычислить поле рассеяния в дальней зоне. Физический смысл теории заключается в том, что поле падающее на некоторый треугольный элемент поверхности не рассеивается в окружающее пространство, а переотражается по законам геометрической оптики в направлении другого треугольного элемента и служит источником возбуждения на нем вторичных электромагнитных волн. Эти электромагнитные волны, рассеиваясь в направлении приемника создают в апертуре приемной антенны дополнительное поле, представленное суммой третьей и пятой компонент в соотношении (1). Основной задачей является определение амплитуды и поляризации электромагнитной волны переотраженной с первого треугольного элемента на второй. На рис. 14 представлена схема переотражения между двумя плоскими треугольниками, расположенными на поверхности объекта.

Рис. 14. Схема переотражения электромагнитной волны между двумя треугольниками.

Падающая на первый треугольник t1 плоская волна под углом падения к нормали отражается из его средней точки M под тем же углом в направлении на треугольник t2. Плоская волна с поляризационным вектором при отражении изменяет направление вектора поляризации. При этом целесообразно представить поляризационный вектор отраженной волны в локальном базисе: , учитывая, что координаты вектора в этом базисе не изменяются при отражении. Следует также отметить, что вектор принадлежит плоскости отражения волны (и соответственно совпадающей с ней плоскостью падения), а вектор ей ортогонален. Характер отражения от первого треугольника в геометрооптическом представлении носит поляризационно зависимый характер, т. е. для соответствующих поляризационных компонент отраженного поля и существуют различные коэффициенты отражения, зависящие от электродинамических параметров и угла падения. Тогда с учетом закона сохранения энергии целесообразно представить поле, отраженное с первого треугольника в направлении на второй в виде совокупности двух плоских волн, соответствующих вертикально и горизонтально поляризованным составляющим: 

где - расстояние от передающей системы до средней точки первого треугольника, - расстояние между средней точкой первого треугольника M и точкой пересечения отраженного луча со вторым треугольником Pr, - угол падения на первый треугольник, - угол падения переотраженного луча на второй треугольник, - площади первого и второго треугольников, - значение функции направленности передающей антенны в направлении на первый треугольник.

Далее задача рассеяния поля вторым треугольником с источниками возбуждения в форме соотношений (13-14) решается с использованием рассмотренного ранее метода физической оптики (2-6). Система координат второго треугольника выбирается в соответствии с рис. 6 с началом в точке пересечения Pr (рис. 14). При этом общее выражение для поля рассеяния в дальней зоне второго треугольника по аналогии с (2) можно представить в следующем виде: 

 где - значение функции направленности приемной антенны в направлении на второй треугольник, - расстояние от приемной системы до точки пересечения переотраженного луча со вторым треугольником Pr, - векторный множитель, функционально зависящий от поляризации падающей на второй треугольник волны, а также электродинамических параметров первого и второго треугольников, ), - проекция вектора на плоскость второго треугольника, - определяется из соотношения (3).

Результирующий вклад от переотражений между элементами сложных объектов (четвертая компонента в (1)) определяется когерентным суммированием вторичных полей рассеяния, определяемых из соотношения (15) для тех треугольных элементов, которые участвуют в переотражениях. Пятая компонента суммарного рассеянного поля (1), характеризующая вклад переоражений между треугольными элементами, принадлежащих как сложному объекту, так и фоновым образованиям, определяется по аналогии с уже рассмотренным методом с той лишь разницей, что вторичное рассеянное поле от фоновых образований определяется с использованием соотношений (9-12) и носит стохастический (случайный) характер. Цифровое моделирование четвертой и пятой компонент осуществляется с помощью объектно-ориентированных методов, которые применялись при расчете первых трех компонент, и уже были рассмотрены ранее. В качестве примера были вычислены характеристики рассеяния идеально проводящего двугранного уголкового отражателя, схема радиолокации которого приведена на рис. 15.

Рис. 15.Схема радиолокации двугранного уголкового отражателя.

Двугранный уголок представляет собой две состыкованные равносторонние пластины (a=16 см), расположенные под прямым углом. Длина волны падающего излучения составляет . Расчет проводился путем когерентного суммирования первой, второй и четвертой компонент результирующего рассеянного поля (1). Другими словами, учитывались вклады треугольных элементов, образующих грани, вклады внешних ребер граней и вклады переотражений между треугольными элементами. При расчете полей рассеяния гладкой части использовались соотношения (2-6), полей рассеяния ребер - (7-8), а компоненты переотражений соотношения (13-15) соответственно. На рис. 16-17 представлены расчетные зависимости (штриховая линия) результирующей ЭПР двугранного уголка в диапазоне углов визирования (0-45)° . Теоретические зависимости ЭПР (сплошная линия) были рассчитаны методом эквивалентных апертур (МЭА) по аналитическим соотношениям приведенным в [6]. Как видно из графиков, теоретические и расчетные зависимости практически не отличаются друг от друга, а максимальная погрешность расчета по сравнению с аналитическим методом не превышает 3%.

Рис. 16. Зависимость суммарной ЭПР двугранного уголка на E-поляризации (штриховая линия - расчет, сплошная линия - теория).

Рис. 17. Зависимость суммарной ЭПР двугранного уголка на H-поляризации (штриховая линия - расчет, сплошная линия - теория).

Приведенные выше расчетные характеристики рассеяния типовых эталонных отражателей в целом совпадают с зависимостями, полученными при тех же условиях с использованием аналитических методов. Средняя погрешность расчета ЭПР различных объектов составляет от 0.02 % до 4 % по сравнению с теоретическими значениями. Соответствующая точность вычисления радиолокационных характеристик эталонов позволяет применить рассмотренный в данной статье метод цифрового моделирования для оценки отражательной способности реальных целей с произвольной геометрической формой и любыми типами электрофизических свойств. При этом единственным условием является наличие разработанной геометрической модели реальной цели и фонового образования в любой из существующих на сегодняшний день САПР, а также электродинамической и статистической модели составляющих цель и фон элементов. В качестве основных достоинств предлагаемой методики следует выделить возможность расчета характеристик рассеяния сложных сцен на любой поляризации передающей и приемной систем (линейной, круговой, эллиптической) как совмещенных, так и разнесенных в пространстве, а также учет сложных зондирующих сигналов с заданным спектром. Кроме того, представляется возможным получить вклады составляющих элементов цели и фона в результирующий отраженный сигнал, что является достаточно важным при оценке радиолокационной заметности цели. Основные ограничения по практической реализации методики могут быть связаны лишь с аппаратными возможностями вычислительных средств и значительными затратами машинного времени в ходе процесса вычислений.

 1. W. B. Gordon. "Far-field approximation of the Kirchhoff-Helmholtz reprezentation of scattered fields", IEEE Trans. Antennas Propagat., vol. AP-23, no. 5, pp. 864-876, July, 1975.

2. A. Michaeli. "Equivalent edge currents for arbitrary aspects of observation", IEEE Trans. Antennas Propagat., vol. AP-23, no. 3, pp. 252-258, Mar., 1984.

6. В. О. Кобак. Радиолокационные отражатели. М.: Советское радио, 1975.

7. П. Я. Уфимцев. Метод краевых волн в физической теории дифракции. М.: Советское радио, 1962.

оглавление

дискуссия