 |
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 3, 2001 |  |
ОБ АБЕРРАЦИЯХ В АПЛАНАТИЧЕСКИХ ЛИНЗОВЫХ АНТЕННАХ
Институт радиотехники и электроники РАН
Получена 28 февраля 2001 г.
Получена формула для оценки фазовых искажений, возникающих в апланатических диэлектрических линзах при смещении облучателя из фокуса. При выводе формулы не использовались приближения параксиальности или "тонкой линзы".
Для нахождения аберраций, зависящих от первой степени величины смещения облучателя из фокуса, воспользуемся приближенным выражением для эйконала луча, прошедшего через двухмерную оптическую систему [1],
,
Где 
- величина поперечного смещения источника из фокуса, 
- угол отклонения
луча луча,вышедшего из источника, от оси системы, L0 –
постоянная составляющая эйконала, у –
поперечная координата.
Представим
Из этого разложения видно, что фронт волны, прошедшей через оптическую систему, является линейным только вблизи оси и основное фазовое искажение (т. н. "кома") имеет кубическую зависимость от у. Максимальная фазовая ошибка при этом на краю линзы и равна:
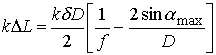
где 
,- волновое число, 
- длина волны в
свободном пространстве, D – диаметр
апертуры антенны, а 
- её угловой размер.
Если система удовлетворяет условию синусов Аббе,
,
т.е. является апланатической, фазовые аберрации, пропорциональные первой степени смещения источника из фокуса равны нулю. В этом случае основной аберрацией в антенне становится астигматизм. Кроме того отметим, что для апланатической линзы величина f является расстоянием от фокуса до кромки линзы.
Для
оценки влияния астигматизма на фазовый фронт на выходе системы ограничимся
рассмотрением осесимметричной линзовой апланатической антенны и рассмотрим
изменение фазы на ее кромке при поперечном смещении облучателя из фокуса на
расстояние 
. Нетрудно показать, что максимальное отклонение от линейного
фронта, сформированного в плоскости сканирования, имеет место в ортогональной
плоскости, где разность эйконалов в центре линзы и на кромке в этой плоскости
равна
,
где
.
Разлагая
полученное выражение в ряд по 
и ограничиваясь тремя членами разложения, получаем
.
Отметим, что при выводе этой формулы не использовались приближения параксиальности или "тонкой линзы" [2,3].
Очень важным следствием данного выражения является факт, что величина астигматизма не зависит от формы преломляющих поверхностей линзы. Иными словами, невозможна реализация линзы без астигматизма.
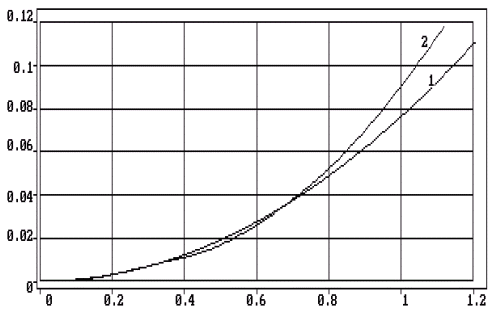
Рис.1
На рисунке 1 кривая 1 показывает зависимость величины аберрации эйконала DL от величины поперечного смещения облучателя, которая рассчитана по последней формуле для следующих параметров линзы D= 3,276, f= 2,6, толщина линзы принималась равной 1 . Кривая 2 на рисунке показывет аналогичную зависимость, рассчитанную в результате численного моделирования линзы с указанными параметрами и коэффициентом преломления равным 1,6.
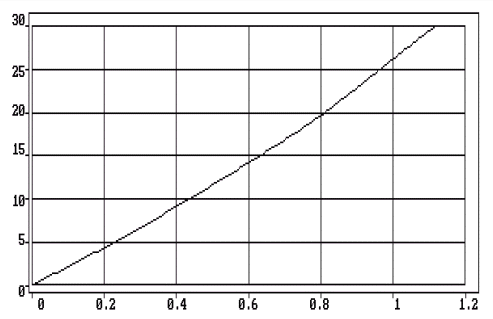
На рисунке 2 изображена зависимость угла отклонения луча в градусах от величины поперечного смещения облучателя. Из рисунков видно, что полученная формула дает удовлетворительные результаты вплоть до углов отклонения 30 градусов.
Рис.2
Полученные формулы остаются справедливыми и для осесимметричных зеркальных антенн. Возможно их обобщение на случай зеркальной антенны с неосесимметричной геометрией. Анализ астигматизма двухзеркальных антенн является более сложным. Однако, как показывают численные исследования [4], избавиться от астигматизма и в таких системах полностью не удается.
В заключение автор приносит благодарность А.С.Венецкому за проведение численных расчетов.
ЛИТЕРАТУРА
-
Я.Н.Фельд, Л.С.Бененсон, Антенно-фидерные устройства, Ч. 2, изд. ВВИА им. Н.Е.Жуковского, 1959, С. 409.
-
Е.Г.Зелкин, Р.А.Петрова, Линзовые антенны, М., Сов. Радио, 1974, С. 65.
-
Л.Д.Бахрах, Зеркальные сканирующие антенны, М., Наука, 1981, С.206-208.
Автор:
д.ф.-м.н. Вадим Анатольевич Калошин, email: vak@cplire.ru
 |
 |