|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 3, 2003 |
|
Анализ схем с операционными усилителями в режиме большого сигнала
Мамедов А. К. оглы, e-mail: mamedov_az50@mail.ru
Азербайджанский Технический Университет
Получена 3 марта 2003 г.
Предложено для приближенной оценки переходной характеристики электронных схем на основе операционных усилителей в режиме большого сигнала использовать метод энергетической линеаризации. Алгоритм построения переходной характеристики продемонстрирован на примере передающего каскада оптоэлектронного устройства с дифференциальным оптроном.
Для оценки динамических параметров электронных схем с обратной связью на основе операционных усилителей (ОУ) в широком диапазоне входных сигналов необходимо учитывать проявляющиеся при этом нелинейные эффекты, связанные с ограниченной величиной скорости нарастания выходного напряжения ОУ. В [1] для анализа частотных характеристик схем на ОУ использован метод гармонической линеаризации. Известно, что прямая интерпретация частотных характеристик системы с точки зрения ее поведения в переходных процессах в общем довольно затруднительна. В настоящей работе для приближенной оценки переходной характеристики электронных схем на основе ОУ в режиме большого сигнала применен метод энергетической линеаризации, разработанный в [2] для определения переходного процесса в замкнутых автоматических системах с одним нелинейным элементом (НЭ).
Использование
метода энергетической линеаризации для анализа электронных схем на ОУ основано
на том, что в режиме большого сигнала ОУ описывается нелинейной моделью,
содержащей один нелинейный элемент с передаточной характеристикой типа
насыщения, который связан с входным дифференциальным каскадом, и
последовательно с ним соединенный интегратор, отражающий частотную зависимость
коэффициента усиления ОУ. В соответствии с этой моделью, схему с обратной связью
на ОУ в частотной области представим в виде, приведенном на рис.I. Здесь ![]() - коэффициент
передачи линейной части схемы с обратной связью,
- коэффициент
передачи линейной части схемы с обратной связью, ![]() -
коэффициент передачи НЭ, называемый коэффициентом энергетической линеаризации. Согласно
определению из [2] этот коэффициент является функцией
амплитуды входного сигнала Vдиф НЭ и
коэффициента демпфирования
-
коэффициент передачи НЭ, называемый коэффициентом энергетической линеаризации. Согласно
определению из [2] этот коэффициент является функцией
амплитуды входного сигнала Vдиф НЭ и
коэффициента демпфирования ![]() . Необходимым условием данного
рассмотрения является наличие такой линейной части системы, при которой
существенное влияние на ее движение независимо от порядка системы оказывают
только две комплексно-сопряженные доминирующие ветви корневого годографа вблизи
(левее) мнимой оси, которым соответствуют два комплексно-сопряженных корня
. Необходимым условием данного
рассмотрения является наличие такой линейной части системы, при которой
существенное влияние на ее движение независимо от порядка системы оказывают
только две комплексно-сопряженные доминирующие ветви корневого годографа вблизи
(левее) мнимой оси, которым соответствуют два комплексно-сопряженных корня ![]() (здесь
s - затухание, w - частота).
(здесь
s - затухание, w - частота).
В режиме малого сигнала, т.е. при Vдиф < Vл, (где Vл - значение Vдиф, соответствующее линейному участку передаточной характеристики НЭ) работа схемы с обратной связью происходит на линейном участке передаточной характеристики НЭ и при выбранном значении коэффициента усиления по петле обратной связи L0, которому соответствуют фиксированные значения параметров s и w, переходная характеристика схемы при указанных выше условиях приближенно описывается выражением
![]()
где Vдиф.о=V(0) - заданное начальное значение сигнала на входе НЭ при t=0.
В режиме большого сигнала, т.е. при Vдиф..0>Vдиф..л, сказывается нелинейность передаточной характеристики НЭ, а
коэффициент усиления по петле обратной связи, равный ![]() ,
становится переменным. Это обуславливает перемещение с течением времени
«изображающей точки»
,
становится переменным. Это обуславливает перемещение с течением времени
«изображающей точки» ![]() по доминирующим ветвям
корневого годографа и, как следствие, изменение во времени параметров s и w затухающего переходного процесса.
по доминирующим ветвям
корневого годографа и, как следствие, изменение во времени параметров s и w затухающего переходного процесса.
Этапы решения указанной задачи продемонстрируем на примере передающего каскада оптоэлектронного устройства с дифференциальным оптроном [3], схема которого представлена на рис.2.
Передаточная функция эквивалентной линеаризованной системы определяется выражением
![]() .
.
В соответствии с рис.2 для Wл(s) нетрудно получить
 ,
,
где ![]() ;
;
![]()
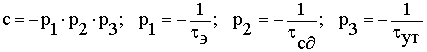
![]() ,
,
Kiдиф - дифференциальный коэффициент передачи по току оптрона;
Kiут - коэффициент передачи по току усилителя тока;
Rвх - входное сопротивление ОУ;
Сфд - емкость фотодиода;
![]() , tут - постоянные времени
светодиода и усилителя тока;
, tут - постоянные времени
светодиода и усилителя тока;
р1, р2, р3 - полюсы передаточной функции Wл(s).
Для конкретности принимаем:
![]()
![]()
![]() .
Здесь fт, Кuo - частота единичного усиления и коэффициент усиления
по напряжению ОУ на нулевой частоте;
.
Здесь fт, Кuo - частота единичного усиления и коэффициент усиления
по напряжению ОУ на нулевой частоте; ![]() - скорость нарастания
выходного напряжения ОУ; Vвх - амплитуда
входного сигнала устройства.
- скорость нарастания
выходного напряжения ОУ; Vвх - амплитуда
входного сигнала устройства.
Тогда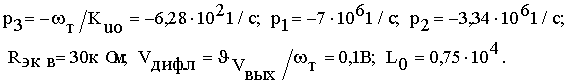
Воспользовавшись известными свойствами корневых годографов [2], построим
годограф рассматриваемой схемы с обратной связью, представленный на рис.3.
Характерные признаки годографа: точка пересечения с действительной осью a= -1,45×106
1/с; число ветвей годографа - 3; углы наклона асимптот - 600, 1800,
3000; точка пересечения асимптот с действительной осью sa= -3,45×106 1/c; точки
пересечения с мнимой осью wкр=±4,9×106
1/с; L0.кр=![]() - значение L0 при w=wкр.
- значение L0 при w=wкр.
На рис.3 нанесены лучи, которым
соответствуют значения z =
0,1; 0,2; ... 1. С учетом выражения  [2], где
[2], где
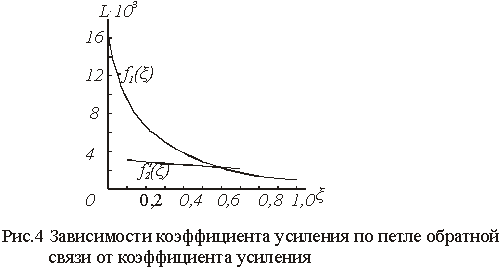
 - длины векторов, проведенных из точек рi в точку s1, определены значения L, соответствующие значениям z, и построена зависимость
- длины векторов, проведенных из точек рi в точку s1, определены значения L, соответствующие значениям z, и построена зависимость  , представленная
на рис.4.
, представленная
на рис.4.
Найдем отношение Vдиф.о/Vдиф.л. Для схемы на рис.2 можно записать
где
На высоких частотах (порядка wт) из (1) и (2) получим
Учитывая исходные данные, из (3) имеем Vдиф.о/Vдиф.л@6.
Найдем точки пересечения кривых ![]() с вертикальной
прямой, проведенной для значения Vдиф.о/Vдиф.л@6,
и в соответствии с выражением
с вертикальной
прямой, проведенной для значения Vдиф.о/Vдиф.л@6,
и в соответствии с выражением
![]() построим
зависимость
построим
зависимость ![]() , представленную на рис.4.
, представленную на рис.4.
Согласно рис.4 точка пересечения кривых ![]() и
и![]() для интервала
для интервала![]() дает
дает ![]() .
.
Тогда ![]() ;
; ![]() ;
;
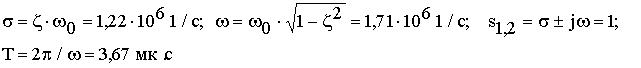 Переходная характеристика подобных систем описывается выражением [2]
Переходная характеристика подобных систем описывается выражением [2]
Учитывая соотношение (4), определим момент t1
прохождения переходной характеристики через нуль и момент t2,
соответствующий ее первому максимальному выбросу: ![]() при
при ![]() ,
откуда t1=1,29мкс;
,
откуда t1=1,29мкс; ![]() при
при
![]() , откуда t2=1,84мкс. В
соответствии с (4) для амплитуды имеем
, откуда t2=1,84мкс. В
соответствии с (4) для амплитуды имеем ![]() .
.
Положив![]() , производим аналогичный расчет для второго интервала.
Так как
, производим аналогичный расчет для второго интервала.
Так как ![]() , то в дальнейшем НЭ работает на линейном участке
передаточной характеристики, а ОУ функционирует в режиме малого сигнала. При
этом частота w и затухание s принимают фиксированные значения. Для
дальнейшего переходного процесса имеем:
, то в дальнейшем НЭ работает на линейном участке
передаточной характеристики, а ОУ функционирует в режиме малого сигнала. При
этом частота w и затухание s принимают фиксированные значения. Для
дальнейшего переходного процесса имеем:
![]()
![]() =3,55×1061/с;
=3,55×1061/с; ![]()
![]() ;
; ![]()
![]() ;.
;. ![]() .
.
Переходная характеристика, построенная по результатам представленного расчета, приведена на рис.5 (кривая 1). В соответствии с кривой 1 время установления переходного процесса tу при допустимой относительной погрешности d=5% равно 3,5мкс. На том же рисунке построена переходная характеристика (кривая 2), соответствующая более грубому приближению в один шаг. При этом параметры переходного процесса после расчета на первом шаге далее считаются неизменными. В соответствии с кривой 2 значение tу равно 2,7мкс. Для сравнения на рис.5 представлена кривая (3), построенная в предположении линейного приближения (z=0,16). Время установления при d=5% составляет 5,4мкс.
Сравнение с экспериментом (время установления равно 3,6мкс) показывает, что приближение в 2 шага дает наиболее хорошее совпадение.
Список литературы
1.P.E.Allen. Slew induced distortion in operational amplifiers//IEEE Journal of solid-state circuits, 1977, v. sc.-12, ¹1, p.39-44.
2.Удерман Э.Г. Метод корневого годографа в теории автоматических систем. - М.: Наука, 1972. - 448с.
3.Носов Ю.Р., Сидоров А.С. Оптроны и их применение. – М.: Радио и связь, 1981. - 280с.
|
|
|



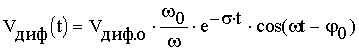 (4)
(4)