 |
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 3, 2004 |
 |
ОПТИМИЗАЦИЯ МОДЕРНИЗАЦИИ РАДИОЛОКАЦИОННОЙ СИСТЕМЫ В УСЛОВИЯХ КОНФЛИКТНОГО ПРОТИВОДЕЙСТВИЯ
А. А. Строцев
Ростовский военный институт ракетных войск
Получена 03 марта 2004 г.
В статье рассмотрен вопрос теоретико-игровой оптимизации модернизации радиолокационной системы по критериям максимальной гарантированной и средней эффективности. Показано, что такой подход к распределению ресурсов позволяет обеспечить рациональность их расходования для практических конфликтных условий применения РЛС.
Содержание
3. Оптимальное распределение ресурсов модернизации
1. Введение
Применение радиолокационных систем (РЛС) в реальных условиях всегда проходит в условиях конфликта (при наличии реального противника или с учётом природных явлений, т. н. «игры с природой»). Постановки задач оптимизации различных режимов функционирования РЛС в таких условиях формализуются моделями теории игр и рассмотрены, например, в [1] – [4]. Как правило, усовершенствование реальных систем ограничено определёнными ресурсами (финансовыми, временными и др.). Обычно задачу оптимизации плана доработок решают исходя из критериев, описывающих некоторые параметры системы. С другой стороны, исходя из конфликтных условий применения РЛС и применяемых моделей конфликта, такой план должен быть оптимизирован по теоретико-игровым критериям. Ясно, что алгоритм оптимизации и его результаты будут зависеть от вида критерия оптимальности, который в свою очередь определяется моделью игровой ситуации. По простоте реализации и изученности среди моделей конфликта выделяются модели матричных игр. Однако и условия их применения ограничены.
Таким образом, исследование возможности синтеза оптимального плана модернизации радиолокационной системы по теоретико-игровым критериям, основанным на модели конфликта в виде матричных игр, в условиях ограничений на ресурсы и технологические возможности является актуальной задачей.
2. Постановка задачи
Рассмотрим
радиолокационную систему, эффективность которой в конфликтной ситуации
определяется матрицей игры
, 
, с элементами 
, 
, 
, где 
– число вариантов управления РЛС, 
– число вариантов
действий противника. Известны функции 
, , , характеризующие приращение эффективности
РЛС, где 
–
количество ресурсов, идущих на совершенствование РЛС, функционирующей при i– ом варианте управления РЛС и при j – ом варианте действий противника.
Общее количество ресурсов ограничено значением S, т. е.
(1)
Требуется распределить ресурсы на модернизацию РЛС в соответствии с теоретико-игровым подходом.
3. Оптимальное распределение ресурсов модернизации
Ясно, что критерий оптимальности распределения ресурсов связан с моделью игры. В условиях поставленной задачи можно выделить три модели: собственно матричную игру и смешанное расширение матричных игр классического и неклассического типов. Они отличаются видом функции выигрыша, причём смешанное расширение матричной игры неклассического типа при определенных условиях обобщает первые две модели [5].
Для поэтапного
исследования применения теоретико-игрового подхода к распределению ресурсов
рассмотрим критерий увеличения максимальной гарантированной эффективности,
соответствующий первой из рассматриваемых моделей. И хотя сама по себе
ситуация, формализуемая этой моделью игры, в реальности складывается редко, но
этот критерий является составной частью критерия, используемого в более общей
модели и, кроме того, во второй модели он имеет самостоятельное значение как
нижнее значение игры 
.
Критерий максимизации максимальной гарантированной эффективности РЛС по результатам модернизации можно представить в виде
(2)
Алгоритм решения задачи (1), (2) несложно получить на основе анализа элементов матрицы игры:
1. Определение оценочных функций для начальной матрицы игры
(3)
2. Определение индекса стратегии управления РЛС, для которой
(4)
Выражения (3), (4) соответствуют вспомогательному шагу алгоритма.
3.
Номер шага
алгоритма 
.
4. Определение индексов вариантов действий противника, для которых
(5)
(6)
5.
Определение 
как решение задачи
(7)
(8)
(9)
6. Если в результате решения (7) – (9) происходит любое из событий:
a) неравенство (8) выполнится как равенство;
b) неравенство (9) выполнится как строгое;
то выход из алгоритма.
Если в результате решения (7) – (9) выполняются условия
(10)
то
выполняется следующий шаг алгоритма (
):
7. Определяется (аналогично выражениям (5), (6)) индекс
(11)
и значения 
, 
как решения задачи
(12)
(13)
(14)
(15)
Условия окончания решения и перехода к следующему шагу аналогичны п. 6 с учётом замены выражений (8) – (10).
Для произвольного значения k выражения (11) – (15) принимают вид:
(16)
(17)
(18)
(19)
Анализ решения задачи распределения ресурсов на модернизацию РЛС по критерию максимума нижнего значения игры показывает, что:
1. Выполнение условия a) из п. 6 (и аналогичных на последующих шагах алгоритма) свидетельствует об израсходовании всех ресурсов на модернизацию.
2. Выполнение условия b) из п. 6 (и аналогичных на
последующих шагах алгоритма) свидетельствует о том, что дальнейшее увеличение
нижнего значения игры невозможно из-за вида функций 
(какие бы ресурсы не были бы
потрачены на модернизацию, эффективность РЛС для этих условий функционирования
не может быть повышена).
3. Если функции монотонно возрастают до
некоторых величин, а ресурсов для модернизации достаточно, то решение задачи
сводится к формированию универсальной стратегии равноэффективной ко всем
возможным действиям противника.
4. Если функции имеют тенденцию к
насыщению, то справедлива постановка вопроса о введении ограничения,
характеризующего эффективность затрат ресурсов.
Рассмотрим теперь в
качестве критерия максимизацию среднего выигрыша (
), соответствующую модели смешанного
расширения матричных игр. Такая задача может быть сформулирована следующим
образом –
найти
(20)
где 
, , 
, , 
, 
и они образуют смешанные стратегии 
, 
, соответственно, для первого и
второго игроков,
при наличии ограничений (1).
Рассмотрим решение задачи
(20), (1) для игр размерности 
при условии, что матрица игры не имеет
седловых точек.
Тогда с применением аналитического метода решения игр такого типа получим эквивалентную (20), (1) задачу оптимизации:
найти
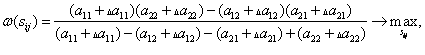(21)
при ограничениях
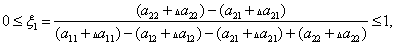(22)
(23)
(24)
Для задач (20), (1) большой размерности, следуя, например, [6], несложно получить следующую задачу нелинейного программирования
найти
(25)
при ограничениях (1) и
(26)
где 
- вектор, размерности n, каждая компонента которого равна
единице, 
- j-ый столбец матрицы A, 
- вектор вспомогательных переменных, 
, 
- j-ый столбец матрицы 
, состоящей из элементов 
.
Нахождение оптимального значения
игры осуществляется
по выражению:
(27)
где 
- решение задачи (25), (26), (1).
4. Иллюстрация на примере
В
качестве примера оптимизации распределения ресурсов рассмотрим задачу с РЛС,
эффективность функционирования которой в конфликтной ситуации определяется
матрицей игры
.
Пусть критерий оптимальности соответствует выражению (20),
(28)
а решение получим для различных значений S в ограничении (1).
До проведения
модернизации имеем 
,
, 
. Результаты решения
задачи оптимального распределения ресурсов представлены в табл. 1.
Таблица 1
Результаты решения
|
Сумма затрат на модернизацию |
0,0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
5,0 |
10,0 |
|
Значение игры |
0,4717 |
0,5093 |
0,5556 |
0,5835 |
0,6104 |
0,6355 |
0,8122 |
0,9368 |
|
Нижнее значение игры |
0,4600 |
0,4800 |
0,5500 |
0,5835 |
0,6104 |
0,6355 |
0,8122 |
0,9368 |
|
Приращение значения игры на единицу затрат |
|
0,1884 |
0,2312 |
0,1397 |
0,1343 |
0,1256 |
0,0442 |
0,0249 |
Оптимальное распределение
ресурсов для 
представляет
собой матрицу с 
,
и остальными 
. При этом 
. Для 
имеем 
, 
, 
, а остальные . Таким образом, при последовательной
оптимизации (например, при поэтапном выделении ресурсов на модернизацию)
результат получится в общем случае хуже, чем при оптимальном распределении суммарных
ресурсов.
Отметим, что с ростом S уменьшается эффективность вложений ресурсов. Кроме того, при больших значениях S и отсутствия ограничений на приращения эффективностей стратегий первого игрока относительно всех стратегий второго игрока наблюдается эффект «универсальной стратегии», т.е. ресурсы модернизации распределяются на совершенствование одной стратегии РЛС так, что она становится одинаково эффективной против любых стратегий противника. При этом максимальная гарантированная и средняя эффективности РЛС сравниваются.
5. Заключение
Таким образом, теоретико-игровая оптимизация плана модернизации радиолокационной системы возможна по критериям, основанным на модели конфликта в виде матричных игр. При этом учитываются ограничения на ресурсы и технологические возможности. Кроме того, рассмотренный подход также позволяет оценить эффективность расходования ресурсов, что особенно актуально, в условиях их ограниченности.
Литература
1. Малышев В.В., Красильщиков М.Н., Карлов В.И. Оптимизация наблюдения и управления летательных аппаратов. – М.: Машиностроение, 1989.
2. Строцев А.А. Оптимизация управления многопозиционной РЛС на основе применения аппарата смешанного расширения матричных игр "неклассического" типа // Журнал радиоэлектроники, 2001, №9.
3. Строцев А.А. Условия применения матричных игр для оптимизации управления многопозиционной РЛС // Журнал радиоэлектроники, 2001, №10.
4. Строцев А.А. Теоретико-игровая модель процесса поиска-уклонения в системе «большая поисковая система – летательный аппарат» // Авиакосмическое приборостроение, 2004, №2.
5. Строцев А.А. Построение смешанного расширения матричной игры «неклассического» типа / Изв.АН. Теория и системы управления, 1998, №3.
6. Воробъёв Н.Н. Теория игр для экономистов-кибернетиков. – М.: Наука, 1985.
 |
 |