| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 3, 2004 |
|
Моделирование ближнего поля зеркальной антенны и его измерений датчиком в виде электрического вибратора
А.Г. Давыдов,
В.А. Калошин,
Институт радиотехники и электроники РАН
Получена 15 марта 2004 г.
На основе численного решения гиперсингулярных интегральных уравнений найдено распределение электрического поля в двух главных плоскостях однозеркальной антенны в ближней зоне. Полученное распределение сравнивается с результатами моделирования измерений этого поля с помощью датчика в виде электрического вибратора. Для моделирования используются два метода: численное решение гиперсингулярных интегральных уравнений и высокочастотное асимптотическое приближение. Проведен анализ полученных результатов.
Введение
Структура ближнего поля зеркальных антенн представляет большой интерес для практики. Знание этой структуры требуется при исследовании взаимного влияния близко расположенных антенн, при проектировании конструктивных элементов антенн – опор, подвесок и т.д., при восстановлении ДН по измерениям ближнего поля и во многих других случаях. Расчет ближнего поля даже при современном уровне развития вычислительной техники и методов решения соответствующих задач возможен далеко не всегда и ограничен сложностью конструкции и размерами антенн. Часто единственной возможностью является экспериментальное исследование ближнего поля. Такие измерения имеют специфические особенности, существенно влияющие на получаемые результаты. В частности, весьма важным является выбор датчика поля. Большой интерес при этом представляет характер влияния конструкции датчика на точность измерения. В настоящей работе проводится численное и асимптотическое моделирование электрического поля и результатов его измерений датчиком в виде электрического вибратора в ближней зоне однозеркальной антенны такой конструкции и размеров, для которых возможно получение достаточно достоверных численных результатов обоими методами.
Численное моделирование поля
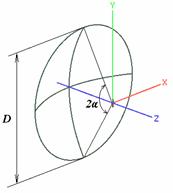
Рассмотрим модель антенны в виде параболического зеркала с
углом раскрыва
![]() ,
диаметром
,
диаметром
![]() и
облучателем в виде полуволнового электрического вибратора (рис.1).
и
облучателем в виде полуволнового электрического вибратора (рис.1).
Для такой антенны диаметром восемь длин волн (![]() ) на основе решения
гиперсингулярных интегральных уравнений [1] было рассчитано распределение поля
в ближней зоне. При этом решалось трехмерное уравнение вида
) на основе решения
гиперсингулярных интегральных уравнений [1] было рассчитано распределение поля
в ближней зоне. При этом решалось трехмерное уравнение вида
где ![]()
![]() ,
, ![]() – расстояние между
точкой наблюдения М и интегрирования
– расстояние между
точкой наблюдения М и интегрирования
![]() , а
, а
![]() - поверхностный импеданс. Под функцией
- поверхностный импеданс. Под функцией
![]() в данном случае
понимается поле источника в виде дельта-функции, э.д.с которого приложена к
центру вибратора (поверхностный импеданс полагается в данном случае равным
нулю). Расчеты проводились методом Галеркина на основе программного комплекса
[2] c использованием кусочно-линейных базисных и пробных
функций [3], обеспечивающих более высокую точность по сравнению с
кусочно-постоянной аппроксимацией.
в данном случае
понимается поле источника в виде дельта-функции, э.д.с которого приложена к
центру вибратора (поверхностный импеданс полагается в данном случае равным
нулю). Расчеты проводились методом Галеркина на основе программного комплекса
[2] c использованием кусочно-линейных базисных и пробных
функций [3], обеспечивающих более высокую точность по сравнению с
кусочно-постоянной аппроксимацией.
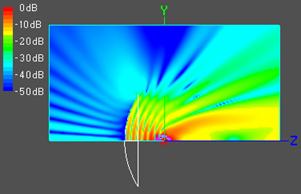
На рисунке 2 в области
![]() с использованием цветовой шкалы показано
двумерные распределения составляющих напряженности полного электрического поля
антенн с углом раскрыва
с использованием цветовой шкалы показано
двумерные распределения составляющих напряженности полного электрического поля
антенн с углом раскрыва
![]() (слева) и
(слева) и
![]() (справа). Верхние рисунки приведены для
плоскости E, нижние – для плоскости H.
Все диаграммы нормированы на одинаковую величину, т.е. приведены в одинаковом
цветовом масштабе.
(справа). Верхние рисунки приведены для
плоскости E, нижние – для плоскости H.
Все диаграммы нормированы на одинаковую величину, т.е. приведены в одинаковом
цветовом масштабе.
Распределение составляющей Ey в плоскости Е

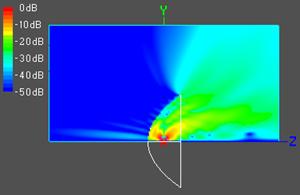
Распределение составляющей Ez в плоскости Е
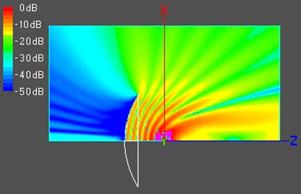
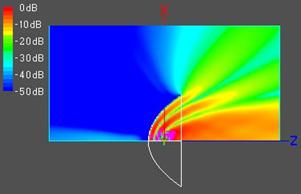
Распределение составляющей Ey в плоскости Н
Рис. 2.
Отметим некоторые особенности показанных распределений поля.
Как видно из рисунка, поле у антенны в области глубокой тени (заднее излучение), за исключением точек вблизи оси, в плоскости H заметно слабее, чем в плоскости E, а в области полутени (боковое излучение) - наоборот. Первое обстоятельство связано с различным видом диаграмм направленности краевых волн металлической кромки в Е и Н плоскости, а второе – с различной формой диаграммы направленности облучателя в этих плоскостях. Естественно, что поле за антенной с более глубоким зеркалом (рис.2, справа) оказывается значительно слабее, чем за более мелким (рис.2, слева), что связано с более эффективным экранированием поля облучателя и краевых волн глубоким зеркалом. По этой же причине ослабляются интерференционные осцилляции их волн, что особенно заметно в Н плоскости.
Параметры одной из антенн подобраны таким образом, чтобы
продемонстрировать любопытный эффект, связанный с интерференцией поля
облучателя и поля, отраженного от зеркала: в освещенной зоне на оси антенны
имеется провал (область
![]() , рис.2 слева).
, рис.2 слева).
Моделирование измерений ближнего поля
При экспериментальном исследовании ближнего поля по существу
измеряется величина коэффициента передачи или электромагнитной связи между
вибратором V1 ( облучателем антенны ) и вибратором V2,
используемым в качестве измерительного датчика. Под значением коэффициента
электромагнитной связи
![]() будем далее понимать отношение мощности,
излученной вибратором антенны, к мощности, поступившей в согласованную нагрузку
приемного вибратора. Можно показать, что этот коэффициент связи (в децибелах)
выражается формулой
будем далее понимать отношение мощности,
излученной вибратором антенны, к мощности, поступившей в согласованную нагрузку
приемного вибратора. Можно показать, что этот коэффициент связи (в децибелах)
выражается формулой
где
![]() -
ток в центре нагруженного на согласованную нагрузку приемного вибратора,
-
ток в центре нагруженного на согласованную нагрузку приемного вибратора,
![]() - ток
в центре вибратора антенны.
- ток
в центре вибратора антенны.![]()
Для определения численным методом коэффициента связи между
вибраторами решалось интегральное уравнение (1) для узкого полоскового
вибратора резонансной длины, выбранной так, чтобы его входное сопротивление
было чисто активным (длина вибратора при этом составила около 0.47λ),
причем в качестве функции
![]() в правой части уравнения использовалось
распределение поля, показанное на рис.2. Для получения результатов,
соответствующих проведению эксперимента, в данном случае необходимо учитывать
влияние входного сопротивления приемника. Это достигается добавлением
сосредоточенной нагрузки, равной по величине активному сопротивлению вибратора
(73 Ома). При решении уравнений такая нагрузка учитывается введением отличного
от нуля поверхностного импеданса
в правой части уравнения использовалось
распределение поля, показанное на рис.2. Для получения результатов,
соответствующих проведению эксперимента, в данном случае необходимо учитывать
влияние входного сопротивления приемника. Это достигается добавлением
сосредоточенной нагрузки, равной по величине активному сопротивлению вибратора
(73 Ома). При решении уравнений такая нагрузка учитывается введением отличного
от нуля поверхностного импеданса
![]() соответствующей величины на части
вибратора в небольшой окрестности его центра.
соответствующей величины на части
вибратора в небольшой окрестности его центра.
Для сопоставления результатов измерений электромагнитной связи с напряженностью поля встает вопрос о соответствующем коэффициенте пропорциональности. Для определения этого коэффициента можно использовать следующую процедуру. Вначале с помощью численного решения уравнения (1) определяется ток j0 в приемном вибраторе, соответствующий падению плоской волны с напряженностью электрического поля Е0=1 В/м. Тогда для произвольного значения E в силу линейности уравнений Максвелла
![]()
где j – ток в приемном вибраторе, соответствующий значению поля E. С другой стороны, из (2)
![]() ,
,
где j* - ток в передающем вибраторе антенны. Вычитая из первого соотношения второе, находим
![]() ,
,
где
![]() .
.
Таким образом, для пересчета значений
![]() коэффициента электромагнитной связи в
значения напряженности поля в соответствующих точках требуется знать лишь
постоянную b, которая легко находится через значения j0 и j*.
коэффициента электромагнитной связи в
значения напряженности поля в соответствующих точках требуется знать лишь
постоянную b, которая легко находится через значения j0 и j*.
Для определения коэффициента электромагнитной связи на основе асимптотического подхода использовались результаты работы [4], в соответствии с которыми в рассматриваемом случае в плоскостях E и H
где
![]() и
и
![]() - коэффициенты усиления первого и
второго вибраторов, а величины
- коэффициенты усиления первого и
второго вибраторов, а величины
![]() , учитывающие дифракцию на первой и второй
кромках зеркала в плоскостях E и H, определяются соотношением
, учитывающие дифракцию на первой и второй
кромках зеркала в плоскостях E и H, определяются соотношением
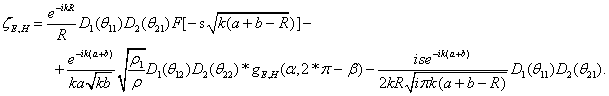
В этом
соотношении
![]() ,
,
![]() ,
,
![]() – комплексный интеграл
Френеля от аргумента u,
– комплексный интеграл
Френеля от аргумента u,
![]() и
и
![]() – нормированные диаграммы направленности
вибраторов. Входящий в (3) коэффициент
– нормированные диаграммы направленности
вибраторов. Входящий в (3) коэффициент
![]() учитывает переход соответствующего луча
через осевую каустику; он равен –i, если рассматриваемый луч переходит через
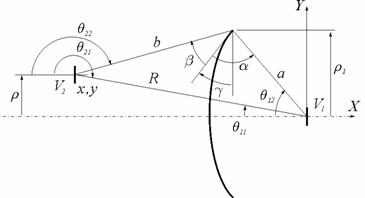
ось Z, и равен 1 в противном случае. Смысл остальных
параметров можно понять из рисунка 3.
учитывает переход соответствующего луча
через осевую каустику; он равен –i, если рассматриваемый луч переходит через
ось Z, и равен 1 в противном случае. Смысл остальных
параметров можно понять из рисунка 3.
Рис. 3
Результаты расчетов
На рисунке 4 приведены полученные описанным путем результаты
расчетов для зеркальной антенны с углом раскрыва
![]() в плоскости H.
Точка наблюдения и приемный вибратор перемещались по дуге окружности радиуса
7.5 λ, причем вибратор сохранял ориентацию параллельно оси Y. По оси абсцисс отложен угол
в плоскости H.
Точка наблюдения и приемный вибратор перемещались по дуге окружности радиуса
7.5 λ, причем вибратор сохранял ориентацию параллельно оси Y. По оси абсцисс отложен угол
![]() , определяющий направление от
начала координат на приемный вибратор. Голубая утолщенная кривая показывает
величину модуля составляющей Ey поля, полученную
непосредственным расчетом, зеленая - на основе асимптотического расчета
электромагнитной связи и красная - на основе численного моделирования измерений
ближнего поля.
, определяющий направление от
начала координат на приемный вибратор. Голубая утолщенная кривая показывает
величину модуля составляющей Ey поля, полученную
непосредственным расчетом, зеленая - на основе асимптотического расчета
электромагнитной связи и красная - на основе численного моделирования измерений
ближнего поля.
Как видно, полученные на основе численного моделирования данные хорошо совпадают друг с другом – различия кривых на графике практически незаметны.
Результаты асимптотического моделирования хорошо совпадают с полученными
численными методами в области около
![]() , а за пределами этой области имеют
заметные отличия, что обусловлено погрешностями асимптотических формул. Прежде
всего это окрестность оси Z (соотношения [4] не предназначены для использования в окрестности
осевой каустики), а также область и
, а за пределами этой области имеют
заметные отличия, что обусловлено погрешностями асимптотических формул. Прежде
всего это окрестность оси Z (соотношения [4] не предназначены для использования в окрестности
осевой каустики), а также область и ![]() 1300 , поскольку асимптотические
выражения [4] справедливы только для области тени.
1300 , поскольку асимптотические
выражения [4] справедливы только для области тени.
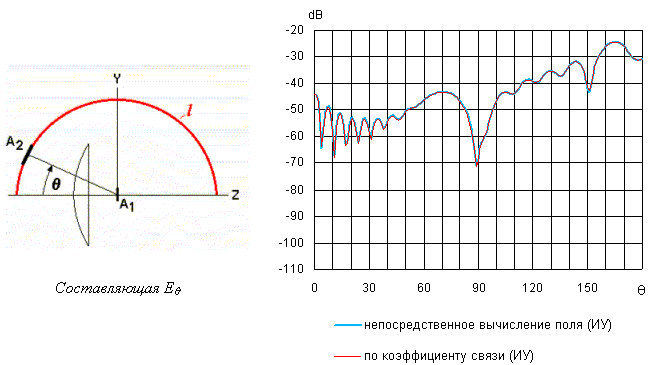
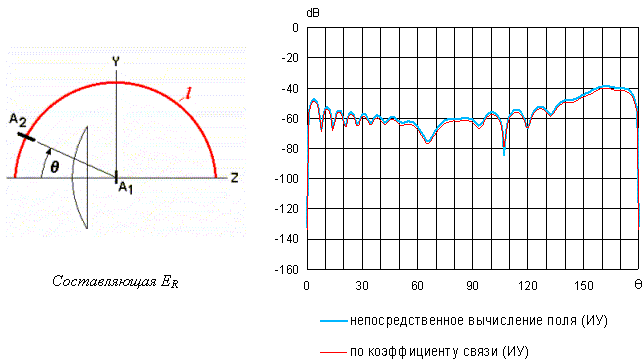
Рис.4. Плоскость Н
На рисунке 5 приведены соответствующие результаты для плоскости E.
Как видно, в этом случае расхождение приведенных кривых более выражено.
Различие результатов, полученных на основе численного моделирования поля, и
результатов моделирования измерений в окрестности
![]() =900 можно объяснить влиянием
конечных размеров приемного вибратора. Различные участки поверхности вибратора
возбуждаются с различными фазами, что приводит к ослаблению принимаемого им
сигнала.
=900 можно объяснить влиянием
конечных размеров приемного вибратора. Различные участки поверхности вибратора
возбуждаются с различными фазами, что приводит к ослаблению принимаемого им
сигнала.
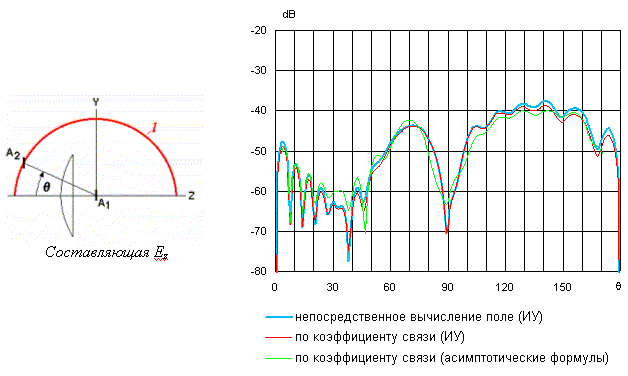
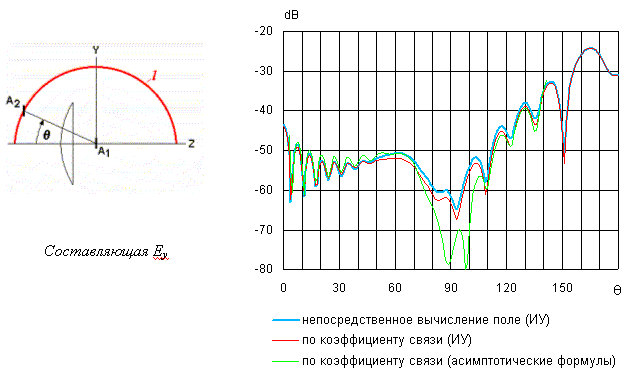
Рис.5. Плоскость E
Этот эффект особенно выражен при
![]() =900, когда волновой
фронт поля ортогонален оси приемного вибратора. Наиболее наглядно это
проявляется, если рассматривать составляющие
=900, когда волновой
фронт поля ортогонален оси приемного вибратора. Наиболее наглядно это
проявляется, если рассматривать составляющие
![]() и
и
![]() (рис.6).
(рис.6).