|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 1, 2006 |
УДК 621.396.962.21
Многоракурсное зондирование в подповерхностной радиотомографии и определение показателя преломления фоновой среды
СУХАНОВ Д.Я., ЯКУБОВ В.П.
Томский государственный университет
Получена 25 марта 2006 г.
Multi-angle
sounding in subsurface radiotomography and determination of background
refraction coefficient of the medium
Sukhanov D.Y.,
Yakubov V.P.
Предлагается решение задачи восстановления распределения неоднородностей под поверхностью земли на основе данных многопозиционного сверхширокополосного радиозондирования. Используется метод радара с синтезированной апертурой с фокусировкой в приповерхностные точки среды. Метод позволяет бесконтактно обнаруживать металлические и диэлектрические рассеивающие объекты под землёй. Также предложен метод бесконтактного определения показателя преломления среды. Приведена математическая модель и оценка разрешающей способности рассматриваемой системы подповерхностного радиотомографа. Работоспособность предлагаемого метода подтверждается экспериментами.
Ключевые слова: радиолокация, георадар, радар с синтезированной апертурой
Введение
Радиолокационные системы для обнаружения объектов под поверхностью земли имеют широкий спектр применений от археологии до поиска пластиковых противопехотных мин. Наиболее перспективным направлением является обнаружение скрытого диэлектрического объекта с помощью сверхширокополосного радиоволнового георадара. Однако при зондировании среды радиоволнами возникает ряд затруднений, связанных со сложностью описания взаимодействия радиоволн со средой и рассеивающими неоднородностями. Имеют место преломление радиоволн на границе раздела сред, сильное затухание радиоволн в земле, дисперсия и многократное рассеяние.
Для исследования неоднородностей скрытых под землей часто используется технология радара с синтезированной апертурой (РСА). При сверхширокополосном многопозиционном зондировании рассеянное излучение содержит наиболее полную информацию о рассеивающих неоднородностях в среде. Для извлечения полезной информации из данных о рассеянном излучении необходимо решение обратной задачи, то есть определение распределения неоднородностей в среде на основе информации об источниках излучения и рассеянном поле. В настоящее время разработано множество методов решения обратной задачи подповерхностной локации на основе технологии РСА [1-8].
Измерения рассеянного поля для синтезирования большой апертуры, в большинстве случаев, сводятся к последовательному перемещению системы из ненаправленных излучающей и приемной антенн в горизонтальной плоскости над поверхностью земли на фиксированной высоте. Для зондирования среды используется сверхширокополосное излучение. Если в среде находится точечный рассеиватель, то зависимость времени возвращения рассеянного импульса от координаты системы антенн будет иметь форму дифракционной гиперболы. По форме и положению дифракционной гиперболы возможно определение координаты рассеивателя.
На практике, часто вместо импульсного сверхширокополосного излучения используется монохроматическое излучение со сканированием в широком диапазоне частот. Далее из частотной области с помощью преобразования Фурье осуществляется переход во временную область. Данные зондирования, преобразованные во временную область эквивалентны данным зондирования среды импульсным излучением.
Оригинальная схема зондирования среды была рассмотрена в работе [1], в которой рассматривается метод, основанный на применении РСА при использовании двумерного углового сканирования антенной системой в верхнем полупространстве. При этом учитывается дисперсия в преломлении и затухании волн в среде зондирования. Обработка данных осуществляется путем фокусировки излучения в каждую точку нижнего полупространства. Последовательное сканирование точкой фокусировки позволяет восстанавливать трехмерное распределение неоднородностей под границей раздела сред. Был проведен тестовый эксперимент с влажным песком и металлическими шариками диаметром 7.62 см, помещенными на глубину 27-67 см в цилиндрический резервуар диаметром 2 м. Рабочий диапазон частот зондирования 2-6 ГГц. Эксперимент подтвердил хорошую работоспособность метода, однако, даже при использовании высокопроизводительного 64-bit процессора на Sun Ultra-1 workstation потребовалось около 4 часов непрерывной обработки данных. Достигнутое реально разрешение оценивается размерами шариков.
В работах [7, 8] был кратко описан быстрый метод восстановления распределения диэлектрических неоднородностей на основе приближения однократного рассеяния в предположении сильного преломления волн на границе раздела сред и метода РСА. Приближение сильно преломляющей среды позволяет восстанавливать распределение неоднородностей путем фокусировки РСА на поверхность среды (операцией свертки) и обратного преобразования Фурье. Этот алгоритм синтезирования апертуры эквивалентен зондированию среды плоскими волнами, распространяющимися вертикально в пределах локализованного радиолуча. Поскольку зондирующие волны распространяются вертикально, то возможно надежное обнаружение преимущественно горизонтальных участков рассеивающих объектов.
В данной работе приводится развернутое описание, оценка разрешающей способности метода, кратко описанного в работах [7, 8], и его развитие для осуществления наклонного сканирования среды и обнаружения негоризонтальных участков рассеивающих объектов. Теоретические выводы сопоставляются с результатами численного моделирования и натурных экспериментов.
Также предлагается новый метод бесконтактного определения среднего показателя преломления среды для случая высоко поднятых антенн при сверхширокополосном радиозондировании. Предлагаемый метод работоспособен практически при любом протяженном распределении рассеивающих неоднородностей без априорной информации о глубине залегания рассеивающих объектов.
Решение прямой задачи подповерхностной радиотомографии
Для построения удобной математической модели примем ряд
приближений. Будем считать, что поверхность земли плоская, земля обладает
высоким средним показателем преломления и можно считать, что преломленные
радиоволны распространяются практически перпендикулярно границе раздела сред.
Неоднородности среды характеризуются относительным изменением диэлектрической
проницаемости ![]() . Рассеяние радиоволн на неоднородностях
рассматривается в скалярном приближении однократного рассеяния.
. Рассеяние радиоволн на неоднородностях
рассматривается в скалярном приближении однократного рассеяния.
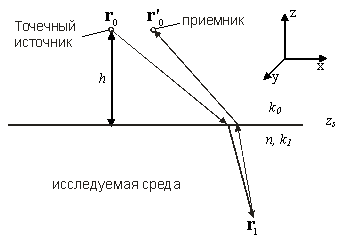
Решение прямой задачи, то есть определение рассеянного поля по заданному распределению неоднородностей в среде, будем рассматривать в частотной области. Рассмотрим точечный источник и приемник, расположенные над поверхностью исследуемой среды (рис. 1). Необходимо определить комплексную амплитуду рассеянного средой поля в точке приема.
|
|
|
Рис. 1 - Траектория распространения зондирующего сигнала |
Если разложить сферическую волну источника по плоским волнам и учесть их преломление на границе раздела сред, то можно записать следующее выражение для поля, проникающего в среду:
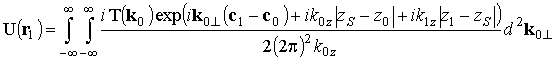 ,
(1)
,
(1)
где ![]() -
коэффициент прохождения границы раздела сред при переходе волны из верхнего
полупространства в нижнее полупространство, который рассчитывается с помощью
формул Френеля;
-
коэффициент прохождения границы раздела сред при переходе волны из верхнего
полупространства в нижнее полупространство, который рассчитывается с помощью
формул Френеля; ![]() ;
; ![]() ;
; ![]() ;
; ![]() -
волновой вектор в верхнем полупространстве;
-
волновой вектор в верхнем полупространстве; ![]() -
волновой вектор в нижнем полупространстве;
-
волновой вектор в нижнем полупространстве; ![]() - пространственный
вектор в горизонтальной плоскости;
- пространственный
вектор в горизонтальной плоскости; ![]() - вертикальная
координата поверхности относительно выбранной системы отсчета;
- вертикальная
координата поверхности относительно выбранной системы отсчета; ![]() -
координата точечного источника над поверхностью среды;
-
координата точечного источника над поверхностью среды; ![]() -
точка в среде.
-
точка в среде.
После проникновения в среду каждая плоская волна рассеивается на неоднородностях. Рассеяние на неоднородностях удобно рассчитать, используя модель однократного рассеяния, при этом каждая рассеивающая неоднородность становится источником сферических волн. Таким образом, рассеянное поле в точке положения приемника можно записать в виде:
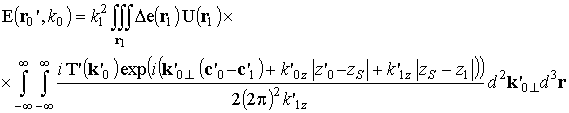 ,
(2)
,
(2)
где ![]() -
коэффициент прохождения границы раздела сред при переходе волны из нижнего
полупространства в верхнее полупространство;
-
коэффициент прохождения границы раздела сред при переходе волны из нижнего
полупространства в верхнее полупространство; ![]() -
координата приемника над поверхностью среды.
-
координата приемника над поверхностью среды.
Выражение (2) представляет собой решение прямой задачи. Но интерес представляет решение обратной задачи, то есть задачи восстановления распределения неоднородностей в среде по рассеянному полю.
Решение обратной задачи подповерхностной радиотомографии
При использовании метода радара с синтезированной апертурой
в широком диапазоне частот существует возможность восстановления объемного
распределения неоднородностей в среде путем обращения интеграла (2). В данном
случае ![]() рассматривается как результат
измерений рассеянного поля методом РСА в горизонтальной плоскости на высоте
рассматривается как результат
измерений рассеянного поля методом РСА в горизонтальной плоскости на высоте ![]() над
поверхностью земли на различных частотах. Считаем, что приемная и передающая
антенны жестко связаны и расположены на расстоянии
над
поверхностью земли на различных частотах. Считаем, что приемная и передающая
антенны жестко связаны и расположены на расстоянии ![]() друг от
друга на высоте
друг от
друга на высоте ![]() над землей.
над землей.
Для решения обратной задачи применим фокусировку рассеянного излучения в приповерхностную точку среды. Операция фокусировки заключается в синфазном сложении рассеянного поля в точке фокусировки. Для обеспечения синфазного сложения необходимо компенсировать фазовые набеги от передающей антенны до точки фокусировки и от точки фокусировки до приемной антенны. Фокусировку рассеянного поля в приповерхностные точки среды можно записать с помощью интеграла свертки:
![]() ,
(3)
,
(3)
![]() ,
(4)
,
(4)
где ![]() - поле,
сфокусированное в приповерхностную точку
- поле,
сфокусированное в приповерхностную точку ![]() ;
; 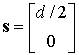 -
вектор смешения антенн по оси
-
вектор смешения антенн по оси ![]() относительно центра
системы приемной и передающей антенн;
относительно центра
системы приемной и передающей антенн; ![]() - расстояние от
передающей антенны до точки фокусировки,
- расстояние от
передающей антенны до точки фокусировки, ![]() -
расстояние от точки фокусировки до приемной антенны. С учетом выражений (1) и
(2):
-
расстояние от точки фокусировки до приемной антенны. С учетом выражений (1) и
(2):
 ,
(5)
,
(5)
где
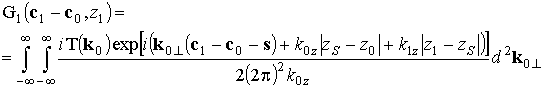 ;
(6)
;
(6)
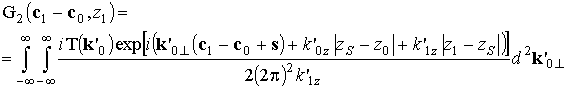 . (7)
. (7)
Примем приближение, что преломленные плоские волны
распространяются перпендикулярно границе раздела сред. Это приближение тем
точнее, чем больше показатель преломления исследуемой среды. При этом ![]() и
и
![]() , следовательно,
, следовательно, ![]() и
и
![]() не зависят от переменных
интегрирования
не зависят от переменных
интегрирования ![]() и
и ![]() в (6) и
(7), то есть,
в (6) и
(7), то есть, ![]() можно вынести за знак интеграла:
можно вынести за знак интеграла:
![]() (8)
(8)
![]() (9)
(9)
Меняя порядок интегрирования в (5) и используя (8) и (9) можно записать:
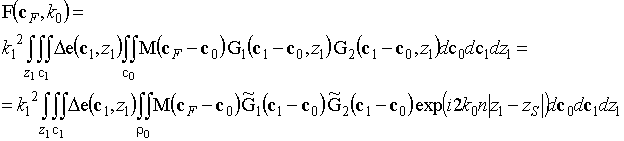 (10)
(10)
Интеграл по ![]() в (10) можно
представить в виде свертки:
в (10) можно
представить в виде свертки:
![]() ,
(11)
,
(11)
где 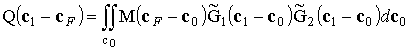 - является
аппаратной функцией системы для монохроматического излучения.
- является
аппаратной функцией системы для монохроматического излучения.
В ходе численных расчетов
значений ![]() , было получено, что
, было получено, что ![]() является
локализованной функцией и в некотором приближении ее можно рассматривать как
дельта функцию. Следовательно, решение интегрального уравнения (11) значительно
упрощается:
является
локализованной функцией и в некотором приближении ее можно рассматривать как
дельта функцию. Следовательно, решение интегрального уравнения (11) значительно
упрощается:
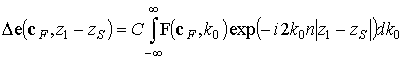 ,
(12)
,
(12)
где ![]() –
постоянный множитель, учитывающий конечную локализацию функции
–
постоянный множитель, учитывающий конечную локализацию функции ![]() .
В результате задача восстановления распределения неоднородностей при
фокусировке излучения в приповерхностную точку среды сводится к операции обратного
преобразования Фурье по вертикальной оси к сфокусированному рассеянному полю.
.
В результате задача восстановления распределения неоднородностей при
фокусировке излучения в приповерхностную точку среды сводится к операции обратного
преобразования Фурье по вертикальной оси к сфокусированному рассеянному полю.
Алгоритм восстановления распределения неоднородностей в
среде состоит в операции свертки с фокусирующей функцией ![]() и
обратного преобразования Фурье. Использование алгоритма быстрого преобразования
Фурье для расчёта интеграла свёртки позволяет значительно ускорить обработку
данных измерений.
и
обратного преобразования Фурье. Использование алгоритма быстрого преобразования
Фурье для расчёта интеграла свёртки позволяет значительно ускорить обработку
данных измерений.
|
|
||
|
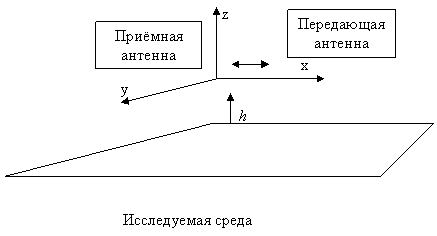
Рис. 2 - Схема измерений |
Использование описанного метода решения обратной задачи предполагает следующую схему проведения измерений (рис. 2). Над плоской поверхностью исследуемой среды на фиксированной высоте в горизонтальной плоскости с определенным шагом перемещается система из излучающей и приемной антенн. В каждой точке производится зондирование среды монохроматическим излучением в широком диапазоне частот с измерением амплитуды и фазы рассеянного поля.
Обозначим через ![]() комплексную
амплитуду измеренного рассеянного поля на частоте
комплексную
амплитуду измеренного рассеянного поля на частоте ![]() при
положении системы излучающей и приемной антенн в точке
при
положении системы излучающей и приемной антенн в точке ![]() .
Тогда получить распределение неоднородностей в среде можно с помощью следующих
операций:
.
Тогда получить распределение неоднородностей в среде можно с помощью следующих
операций:
![]() ,
(13)
,
(13)
где
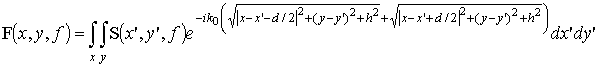 ;
;
![]() – волновое число в среде.
– волновое число в среде.
Для проверки работоспособности предложенного метода и адекватности допущенных упрощений было проведено численное моделирование работы рассматриваемой системы и рассчитана ее аппаратная функция.
Было проведено численное моделирование присутствия точечного
рассеивателя в различных точках среды. Для каждого положения точечного
рассеивателя рассчитывалась реакция системы на его присутствие в случае
использования монохроматического и сверхширокополосного импульсного излучения
при фокусировке системы в фиксированную приповерхностную точку среды.
Рассмотрим случай фокусировки в приповерхностную точку среды, находящуюся под
центром синтезируемой апертуры (т.е. при ![]() ). Аппаратная функция
рассчитывалась согласно следующему выражению:
). Аппаратная функция
рассчитывалась согласно следующему выражению:
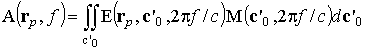 ,
(14)
,
(14)
где ![]() -
результат измерения поля в горизонтальной плоскости в точке
-
результат измерения поля в горизонтальной плоскости в точке ![]() над
поверхностью среды на высоте
над
поверхностью среды на высоте ![]() при положении
точечного рассеивателя в среде в точке
при положении
точечного рассеивателя в среде в точке ![]() ;
; ![]() -
частота излучения;
-
частота излучения; ![]() .
.
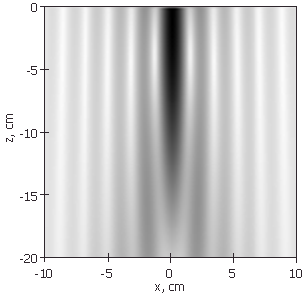
Численный расчет аппаратной функции для показателя преломления n = 3 и монохроматического излучения с частотой 5 ГГц представлен на рис. 2. Из рис. 2 видно, что в действительности аппаратная функция системы изменяется с глубиной, и на большой глубине расходится. Причем с увеличением показателя преломления среды аппаратная функция системы будет сохранять высокую локализацию на больших глубинах.
Применив к ![]() обратное
преобразование Фурье можно получить область в среде, где система обладает
наибольшей чувствительностью к рассеивателю в различные моменты времени при
использовании импульсного излучения:
обратное
преобразование Фурье можно получить область в среде, где система обладает
наибольшей чувствительностью к рассеивателю в различные моменты времени при
использовании импульсного излучения:
 ,
(15)
,
(15)
При этом отклик системы на точечный рассеиватель в среде во
временной области ![]() будет иметь вид локализованной в
пространстве функции. С увеличением времени область наибольшей амплитуды
функции
будет иметь вид локализованной в
пространстве функции. С увеличением времени область наибольшей амплитуды
функции ![]() смещается вниз по вертикальной оси
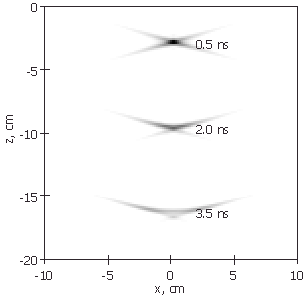
(рис. 3). На рис. 4 представлены функции
смещается вниз по вертикальной оси
(рис. 3). На рис. 4 представлены функции ![]() ,
, ![]() и
и
![]() в вертикальном сечении. На большой
глубине аппаратная функция системы менее локализована в горизонтальных
направлениях. То есть предложенный метод наиболее эффективен в приповерхностной
области среды.
в вертикальном сечении. На большой
глубине аппаратная функция системы менее локализована в горизонтальных
направлениях. То есть предложенный метод наиболее эффективен в приповерхностной
области среды.
|
|
|
|
Рис. 3 - Амплитуда аппаратной функции системы на частоте 5 ГГц |
Рис. 4 - Области наибольшей чувствительности системы в различные моменты времени |
Оценка разрешающей способности
Под разрешающей способностью понимается расстояние между двумя точечными рассеивателями на котором их можно однозначно различить. Разрешающая способность системы можно определить по функции неопределённости, которая аналогична рассмотренной ранее аппаратной функции. Предпочтительно получить аналитическое выражение для разрешающей способности определяемое размером апертуры, полосой частот и высотой антенн над поверхностью среды.
Рассмотрим метод радара с синтезированной апертурой в свободном пространстве для случая одномерной линейной апертуры (рис. 5) и монохроматического излучения. Будем считать, что поле предающей антенны и поле рассеянное точечным рассеивателем описывается функцией Грина в свободном пространстве.
|
|||
|
Рис. 5 - Размещение точечного рассеивателя относительно синтезируемой апертуры |
Разрешающая способность характеризуется через функцию
неопределённости, которая рассчитывается как реакция системы на точечный
рассеиватель. Для вычисления функции неопределенности воспользуемся построением
на рис. 5. В точке ![]() расположен единственный точечный
рассеиватель, порождающий рассеянное поле, которое в точке приёма
расположен единственный точечный
рассеиватель, порождающий рассеянное поле, которое в точке приёма ![]() с
точностью до постоянных множителей имеет следующий вид:
с
точностью до постоянных множителей имеет следующий вид:
![]() ,
,
где ![]() -
волновое число в свободном пространстве,
-
волновое число в свободном пространстве, ![]() - расстояние от
точечного рассеивателя до текущей точки измерения рассеянного поля.
- расстояние от
точечного рассеивателя до текущей точки измерения рассеянного поля.
Операция синтезирования апертуры в этом случае аналитически записывается так:
 ,
(16)
,
(16)
где ![]() -
фактически и является функцией неопределённости.
-
фактически и является функцией неопределённости.
Для вычисления интеграла (16) примем приближение ![]() и
будем рассматривать операцию фокусировки при
и
будем рассматривать операцию фокусировки при ![]() .
.
В результате функция неопределённости примет вид:
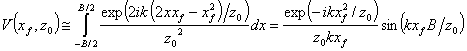
Разрешающая способность определяется из критерия ![]() .
Таким образом, разрешающая способность по горизонтали:
.
Таким образом, разрешающая способность по горизонтали: ![]() .
.
Для импульсного излучения разрешение определяется минимальной длиной волны в спектре сигнала. Поскольку информация о раздельности точечных рассеивателей содержится в высоких частотах спектра сигнала, то очевидно можно сказать, что эта информация содержится и в самом сигнале. То есть разрешение определяется наилучшим разрешением, обеспечиваемым составляющими сигнала.
В предложенном алгоритме (13) восстановления распределения неоднородностей разрешающая способность по горизонтали определяется аналогично, причём в приближении сильно преломляющей среды она не изменяется с увеличением глубины.
Результаты экспериментальных исследований на тестовых объектах
Для проверки предложенного метода восстановления распределения неоднородностей был проведен реальный эксперимент на различных тестовых объектах. В песок на глубину от 1 см до 20 см были помещены три корпуса пластиковых противопехотных мин и ступенчатый объект из вспененного полистирола с размером ступенек 5 см. На рис. 6 представлена фотография объектов.
В ходе измерений использовался диапазон частот от 0,5 ГГц до 17 ГГц. Система из приемной и передающей антенн перемещалась с шагом 1 см по горизонтальной плоскости в квадрате 50x50 см2 на высоте 30 см. Расстояние между антеннами составляло 14 см.
Используя формулы (12) удалось восстановить приближенную форму тестовых объектов (рис. 7). Для улучшения визуального качества изображений использовалась линейная фильтрация сигнала для увеличения амплитуды на высоких частотах.
|
|
|
|
Рис. 6 - Тестовые объекты |
Рис. 7 - Восстановление распределения неоднородностей |
Из представленных рисунков видно, что предложенный метод для описанной установки имеет разрешение порядка 1 см до глубины 11 см. Объект 4 помещенный на глубину 20 см обнаружить не удалось, что связано с затуханием сигнала в среде и расхождением аппаратной функции системы на больших глубинах.
Метод наклонной фокусировки
Для осуществления наклонного зондирования среды предлагается модификация выше описанного алгоритма восстановления распределения неоднородностей. Наклонная фокусировка РСА способна обеспечить детектирование и негоризонтальных граней рассеивающих объектов.
Для осуществления наклонного сканирования среды предлагается производить фокусировку РСА в приповерхностные точки среды, смещённые относительно центра апертуры на определённое расстояние. При этом эквивалентная траектория распространения зондирующих волн аппроксимируется биссектрисой угла между точкой фокусировки и краями апертуры. Траектория распространения излучения в среде продлевается согласно закону Снеллиуса.
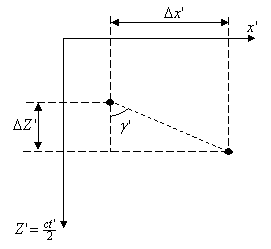
Геометрическая иллюстрация наклонной фокусировки радара с синтезированной апертурой приведена на рис. 8.
|
|
|
Рис. 8 - Наклонная фокусировка и траектория сканирования среды 1 - область
перемещения приёмопередающей антенны; 2 - cинтезируемая апертура; 3 - аппроксимация траектории
распространения волн; 4 - точка фокусировки; |
При условии, что передающая и приемная антенны совмещены, фокусировку рассеянного излучения в приповерхностные точки среды можно записать в виде свёртки:
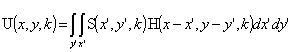 ,
(17)
,
(17)
где 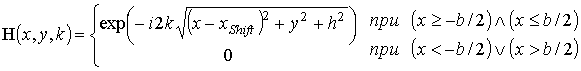 ;
;
![]() -
сдвиг точки фокусировки относительно центра апертуры;
-
сдвиг точки фокусировки относительно центра апертуры;
![]() - размер апертуры;
- размер апертуры; ![]() -
угол поворота апертуры;
-
угол поворота апертуры; ![]() - точки фокусировки системы;
- точки фокусировки системы;
![]() -
расстояние от плоскости апертуры до плоскости фокусировки.
-
расстояние от плоскости апертуры до плоскости фокусировки.
Из построения на рис. 10 видно, что ![]() , и,
следовательно:
, и,
следовательно:
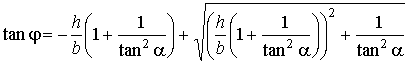 .
.
Условие равенства нулю функции ![]() при
при ![]() и
при
и
при ![]() позволяет синтезировать апертуру
заданного размера
позволяет синтезировать апертуру
заданного размера ![]() (
(![]() должно быть
меньше области перемещения антенн). Чем больше размер апертуры, тем больше
разрешение системы в горизонтальной плоскости, но тем меньше область
поверхности, где наклонная фокусировка работает правильно.
должно быть
меньше области перемещения антенн). Чем больше размер апертуры, тем больше
разрешение системы в горизонтальной плоскости, но тем меньше область
поверхности, где наклонная фокусировка работает правильно.
Чтобы получить трёхмерное распределение неоднородностей в
среде при наклонной фокусировке достаточно осуществить обратное преобразование
Фурье по частоте функции ![]() :
:
![]() ,
(18)
,
(18)
где ![]() -
восстановленное трёхмерное изображение распределения неоднородностей в среде
при наклонной фокусировке. Однако изображение
-
восстановленное трёхмерное изображение распределения неоднородностей в среде
при наклонной фокусировке. Однако изображение ![]() имеет
искажения масштабирования, сдвига и вращения относительно системы координат
измерений. Желательно иметь только преобразование вращения. Для устранения
нежелательных искажений применим следующую операцию:
имеет
искажения масштабирования, сдвига и вращения относительно системы координат
измерений. Желательно иметь только преобразование вращения. Для устранения
нежелательных искажений применим следующую операцию:
![]() ,
,
где ![]() - угол
преломления, соответствующий углу падения
- угол
преломления, соответствующий углу падения ![]() ;
; ![]() –
средний показатель преломления среды; функция
–
средний показатель преломления среды; функция ![]() является
трёхмерным изображением распределения неоднородностей в среде, повернутым
относительно системы координат измерений на угол
является
трёхмерным изображением распределения неоднородностей в среде, повернутым
относительно системы координат измерений на угол ![]() .
.
Представленный алгоритм производит фокусировку излучения только в приповерхностные точки среды и может быть реализован на основе операции быстрого преобразования Фурье, что обеспечивает невысокие требования к вычислительным ресурсам. Кроме того, для работы алгоритма не требуется априорной информации о показателе преломления среды, эта информация необходима только для определения правильной системы координат.
Моделирование аппаратной функции системы при наклонной фокусировке
Для подповерхностного радиотомографа с наклонной
фокусировкой РСА численно была рассчитана аппаратная функция системы для случая
использования монохроматического и сверхширокополосного импульсного излучения.
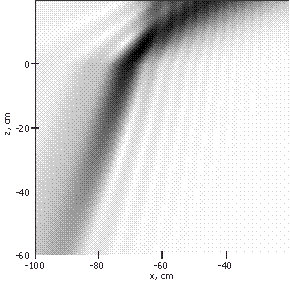
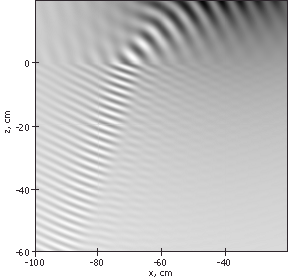
На рисунке 9 и рисунке 10 представлены, соответственно, амплитуда и
действительная часть аппаратной функции системы при использовании
монохроматического излучения 3 ГГц, наклона фокусировки 45° и показателе
преломления среды равным 2. Тёмным цветом изображены области наибольшей
чувствительности системы (области большей амплитуды аппаратной функции).
Величине ![]() соответствует поверхность исследуемой
среды. Видно, что в области наибольшей амплитуды аппаратной функции
зондирование среды подобно зондированию плоскими волнами, распространяющимися
под углом преломления к нормали поверхности.
соответствует поверхность исследуемой
среды. Видно, что в области наибольшей амплитуды аппаратной функции
зондирование среды подобно зондированию плоскими волнами, распространяющимися
под углом преломления к нормали поверхности.
|
|
|
|
Рис. 9 - Амплитуда аппаратной функции при частоте 3 ГГц и n=2 |
Рис. 10 - Действительная часть аппаратной функции при частоте 3 ГГц и n=2 |
На рис. 11 изображена аппаратная функция системы во временной области (импульсная реакция) в различные моменты времени при использовании импульсного излучения со спектром от 0,5 ГГц до 20 ГГц. Как видно из рисунков, аппаратная функция имеет наибольшую амплитуду в локализованной области пространства. С увеличением глубины степень локализации аппаратной функции уменьшается и, как следствие, уменьшается разрешение. Следовательно, при наклонном импульсном зондировании возможно восстановление трёхмерной структуры среды в некоторой приповерхностной области. Причём с увеличением показателя преломления среды увеличивается глубина, где сохраняется высокое разрешение метода.
|
|
|
Рис. 11 - Аппаратная
функция системы в моменты |
Экспериментальные исследования
Для проверки метода наклонной фокусировки в технологии радара с синтезированной апертурой был проведён эксперимент с наклонной металлической пластиной, помещённой в песок (рис. 12).
|
|
|
Рис. 12 - Расположение металлической пластины в песке |
После обработки данных зондирования с помощью алгоритма
наклонной фокусировки были получены изображения (риc. 13 – 14) при наклоне
фокусировки соответственно 0 и 30 градусов. Координате по оси ![]() соответствует
половина времени возвращения зондирующего сигнала, умноженного на скорость
света в вакууме.
соответствует
половина времени возвращения зондирующего сигнала, умноженного на скорость
света в вакууме.
|
|
|
|
Рис. 13 - Восстановленное изображение без наклона фокусировки |
Рис. 14 - Восстановленное изображение при наклоне фокусировки на 30° |
Как видно из представленных рисунков, заложенный объект наиболее отчётливо выделяется при наклоне фокусировки в 30 градусов, то есть когда направление падения волны наиболее близко к нормальному. Таким образом, проводя сканирование среды под разными углами методом наклонной фокусировки можно определить горизонтальные и негоризонтальные участки объекта, скрытого под землёй и восстановить его форму.
Метод определения показателя преломления фоновой среды
Используя информацию о рассеянном поле ![]() можно
определить трехмерное распределение рассеивающих неоднородностей под
поверхностью среды. Выше описанные алгоритмы благодаря фокусировке в
приповерхностную точку среды обеспечивают зондирование среды узким
коллимированным волновым пучком, и не требуют информации о показателе
преломления. При переходе во временную область путем обратного преобразования
Фурье по частоте происходит сканирование среды вдоль оси пучка эквивалентное
зондированию коротким радио импульсом. Таким образом, вертикальной оси на
восстанавливаемом трехмерном изображении неоднородностей должна быть приведена
в соответствие координата, которая равна половине времени возвращения
рассеянного импульса, умноженного на скорость света в среде. Поскольку
показатель преломления среды неизвестен, то для внесения определенности положим
пока его равным единице.
можно
определить трехмерное распределение рассеивающих неоднородностей под
поверхностью среды. Выше описанные алгоритмы благодаря фокусировке в
приповерхностную точку среды обеспечивают зондирование среды узким
коллимированным волновым пучком, и не требуют информации о показателе
преломления. При переходе во временную область путем обратного преобразования
Фурье по частоте происходит сканирование среды вдоль оси пучка эквивалентное
зондированию коротким радио импульсом. Таким образом, вертикальной оси на
восстанавливаемом трехмерном изображении неоднородностей должна быть приведена
в соответствие координата, которая равна половине времени возвращения
рассеянного импульса, умноженного на скорость света в среде. Поскольку
показатель преломления среды неизвестен, то для внесения определенности положим
пока его равным единице.
Для определения действительного показателя преломления среды предлагается использовать вышеописанный алгоритм наклонного сканирования среды. При наклонном сканировании среды угол поворота восстанавливаемого изображения отличается от угла наклонной фокусировки системы антенн, что связано с преломлением волн на границе раздела сред. Этот факт использован для определения показателя преломления среды.
Рассмотрим случай, когда в среде находятся рассеивающие
объекты произвольной формы. Поскольку в алгоритме восстановления распределения
неоднородностей в среде используется волновое число в свободном пространстве,
то получаемые изображения среды будут «растянуты» по вертикальной оси в ![]() раз
(
раз
(![]() - показатель преломления среды). Следовательно, помимо
преобразования поворота изображения, при наклонной фокусировке происходит и
преобразование масштабирования изображения.
- показатель преломления среды). Следовательно, помимо
преобразования поворота изображения, при наклонной фокусировке происходит и
преобразование масштабирования изображения.
На рис. 15 приведена схема сканирования на примере
среды с двумя точечными рассеивателями при ненаклонной и наклонной фокусировке
методом (17, 18), т.е. без устранения искажений. Геометрические построения на
рис. 15 позволяют получить матрицу преобразования системы координат
физического пространства ![]() в пространство изображения
в пространство изображения ![]() при
методе фокусировки (1) для среды с показателем преломления
при
методе фокусировки (1) для среды с показателем преломления ![]() :
:
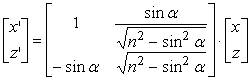 .
(19)
.
(19)
Как можно видеть из (19), преобразование системы координат физического пространства в пространство изображения при наклонной фокусировке (17, 18), совмещает в себе и вращение, и масштабирование даже при показателе преломления равном 1. Это связано с тем, что система антенн перемещается в горизонтальной плоскости.
|
|
|
Рис. 15 - Траектории наблюдения объектов при наклонной и ненаклонной фокусировке 1 – плоскость перемещения приемной и передающей антенн; 2 – точечные рассеиватели; 3 – исследуемая среда с показателем преломления n. |
Однако для определения показателя преломления среды практический интерес имеет матрица линейного преобразования из пространства изображения (A), полученного при ненаклонной фокусировке в пространство изображения (B), полученного при наклонной фокусировке.
На рисунке 16 представлено изображение двух точечных
объектов при ненаклонной фокусировке ![]() . На рисунке 17
представлено изображение двух точечных объектов при наклонной фокусировке
. На рисунке 17
представлено изображение двух точечных объектов при наклонной фокусировке ![]() .
.
Используя геометрические построения рис. 15 - 17 можно получить искомую матрицу преобразования:
 ,
(20)
,
(20)
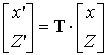 ,
, ![]() ,
,
где ![]() ;
; ![]() ;
; ![]() –
координата по вертикальной оси в физическом пространстве;
–
координата по вертикальной оси в физическом пространстве; ![]() -
координата по оси, наклоненной на угол
-
координата по оси, наклоненной на угол ![]() к вертикали в
физическом пространстве.
к вертикали в
физическом пространстве.
|
|
|
|
Рис. 16 - Схематическое изображение рассеивателей при ненаклонной фокусировке |
Рис. 17 - Схематическое изображение рассеивателей при наклонной фокусировке |
Матрица ![]() включает известный
параметр
включает известный
параметр ![]() - угол наклонной фокусировки и
неизвестный параметр
- угол наклонной фокусировки и
неизвестный параметр ![]() - показатель преломления среды. Таким
образом, если с помощью методов распознавания изображений удастся определить
матрицу линейного преобразования изображения
- показатель преломления среды. Таким
образом, если с помощью методов распознавания изображений удастся определить
матрицу линейного преобразования изображения ![]() к
изображению
к
изображению ![]() , то с использованием вида матрицы
, то с использованием вида матрицы ![]() можно
определить показатель преломления среды. Для решения задачи распознавания
возможно использование метода наименьших квадратов (МНК), если варьировать
значением
можно
определить показатель преломления среды. Для решения задачи распознавания
возможно использование метода наименьших квадратов (МНК), если варьировать
значением ![]() в матрице
в матрице ![]() и
вычислять невязку между изображением
и
вычислять невязку между изображением ![]() и
и ![]() .
.
Поясним работу предложенного метода на рассмотрении простейшего
изображения двух точечных рассеивателей. Определив взаимное положение двух
рассеивающих объектов на восстанавливаемых изображениях (рис. 16, 17)
![]() и
и ![]() при
наклонной и ненаклонной фокусировках можно найти коэффициенты линейного
преобразования
при
наклонной и ненаклонной фокусировках можно найти коэффициенты линейного
преобразования ![]() . Исходя из геометрических построений рис. 15-17 и закона
преломления Снеллиуса можно выразить показатель преломления среды:
. Исходя из геометрических построений рис. 15-17 и закона
преломления Снеллиуса можно выразить показатель преломления среды:
 ,
(21)
,
(21)
Таким образом, для определения показателя преломления для
простейшего случая с двумя точечными рассеивателями необходимо знать угол
наклона фокусировки ![]() , отношение разности глубин двух объектов
на изображениях, полученных при наклонной и ненаклонной фокусировках и тангенс
угла
, отношение разности глубин двух объектов
на изображениях, полученных при наклонной и ненаклонной фокусировках и тангенс
угла ![]() (рис. 17).
(рис. 17).
Для проверки предложенного метода определения показателя
преломления среды, был проведен ряд численных экспериментов. Моделировалось присутствие
двух точечных рассеивателей, расположенных таким же образом, как показано на
рис. 15, но при ![]() .
.
На рис. 18 представлено изображение ![]() двух
точечных рассеивателей при ненаклонной фокусировке. На рис. 19
представлено изображение
двух
точечных рассеивателей при ненаклонной фокусировке. На рис. 19
представлено изображение ![]() , полученное при наклонной фокусировке в 30
градусов. Координате по оси
, полученное при наклонной фокусировке в 30
градусов. Координате по оси ![]() соответствует
половина времени возвращения зондирующего сигнала, умноженного на скорость
света в вакууме. В ходе численного эксперимента были построены изображения
соответствует
половина времени возвращения зондирующего сигнала, умноженного на скорость
света в вакууме. В ходе численного эксперимента были построены изображения ![]() для
различных углов
для
различных углов ![]() наклонной фокусировки. При каждом
угле
наклонной фокусировки. При каждом
угле ![]() с использованием изображения
с использованием изображения ![]() и
изображений
и
изображений ![]() был
рассчитан показатель преломления среды.
был
рассчитан показатель преломления среды.
|
|
|
|
Рис. 18 - Восстановленное изображение рассеивателей при ненаклонной фокусировке |
Рис. 19 - Восстановленное изображение рассеивателей при наклонной фокусировке в 30° |
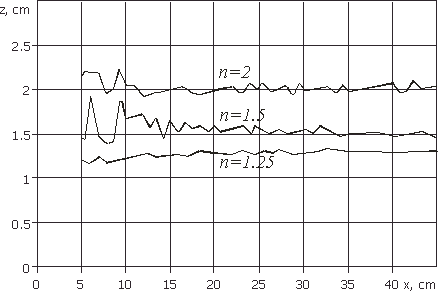
На риc. 20 представлены результаты решения задачи определения показателя преломления среды в соответствии с формулой (21) в зависимости от угла наклона фокусировки для показателей преломления среды 1.25, 1.5 и 2.
|
|
|
Рис. 20 - Результаты определения показателя преломления при различных углах наклонной фокусировки |
Как видно из представленных графиков, метод определения
среднего показателя преломления наиболее точен при больших углах наклона фокусировки.
Низкая точность метода при небольших углах наклонной фокусировки связана с
конечностью разрешения изображений и большей чувствительностью метода к
точности определения коэффициентов линейного преобразования изображения ![]() к
изображению
к
изображению ![]() . Незначительная систематическая ошибка
определения показателя преломления среды для n=1.25 связана с тем, что
аппаратная функция системы при наклонном сканировании имеет высокую локализацию
в небольшом интервале глубин, что приводит к снижению точности определения
коэффициентов линейного преобразования.
. Незначительная систематическая ошибка
определения показателя преломления среды для n=1.25 связана с тем, что
аппаратная функция системы при наклонном сканировании имеет высокую локализацию
в небольшом интервале глубин, что приводит к снижению точности определения
коэффициентов линейного преобразования.
Преимуществом данного метода является возможность
бесконтактного определения показателя преломления среды без использования
априорной информации о расположении рассеивающих объектов в среде. Но для
работы метода необходимо наличие как минимум двух рассеивателей в среде. Однако
метод может быть модифицирован для одного точечного рассеивателя в среде при
наблюдении отражения от поверхности среды. В этом случае: 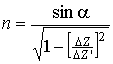 , где
, где
![]() - расстояние от поверхности до
рассеивателя на изображении
- расстояние от поверхности до
рассеивателя на изображении ![]() ;
;
![]() - расстояние от поверхности до
рассеивателя на изображении
- расстояние от поверхности до
рассеивателя на изображении ![]() .
.
Экспериментальная проверка метода определения показателя преломления
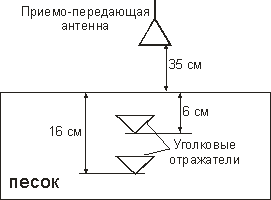
Для проверки предложенного метода был проведен эксперимент по определению среднего показателя преломления сухого песка. В ходе эксперимента в качестве рассеивателей были использованы два уголковых отражателя с ребром 8 см.
Уголковые отражатели были заложены в песок один над другим на глубины 6 см и 16 см. Далее были проведены измерения с помощью РСА в диапазоне частот от 500 МГц до 20 ГГц с шагом перемещения системы приемной и передающей антенн в 1 см, при области перемещения антенн 56 см и высоте антенн над песком 35 см (рис. 21).
|
|
|
Рис. 21 - Размещение уголковых отражателей в сухом песке |
Данные зондирования были подвергнуты обработке методом
наклонной фокусировки для различных углов в диапазоне от 0° до 30° градусов. На
рис. 22 и рис. 23 представлены изображения, полученные при
ненаклонной фокусировке и при наклоне фокусировки в 12° соответственно. В результате обработки изображений, полученных
при различных углах наклона сканирования среды, был определен средний
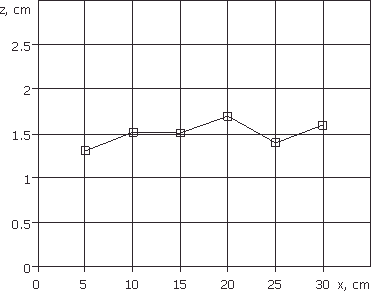
показатель преломления среды. На рис. 24 приведены результаты определения
показателя преломления по экспериментальным данным при различных углах
наклонной фокусировки ![]() . Усредненный по углам поворота фокусировки
показатель преломления равен 1,5.
. Усредненный по углам поворота фокусировки
показатель преломления равен 1,5.
|
|
|
|
Рис. 22 - Изображение уголковых отражателей при ненаклонной фокусировке |
Рис. 23 - Изображение уголковых отражателей при наклонной фокусировке |
|
|
|
Рис. 24 - Результат определения показателя преломления |
Поскольку в поставленном эксперименте уголковые отражатели были заложены на глубину 6 см и 16 см, а расстояние между ними на изображении при ненаклонной фокусировке, полученном в предположении, что показатель преломления среды равен 1, составило 15 см (рис. 22), то показатель преломления песка действительно равен 1,5.
Таким образом, результат эксперимента по определению среднего показателя преломления среды методом наклонной фокусировки подтвержден.
Заключение
В работе предложен быстродействующий метод восстановления распределения неоднородностей скрытых под поверхностью земли с помощью сверхширокополосного радиозондирования, основанный на технологии радара с синтезированной апертурой.
Предложенный метод восстановления неоднородностей обладает высоким быстродействием благодаря возможности использования быстрого преобразования Фурье. Наибольшая разрешающая способность обеспечивается при широкой полосе используемых частот и большой апертуре. Работоспособность метода подтверждается данными натурных экспериментов по томографии диэлектрических объектов, находящихся во влажном песке. Показано, что при использовании частотного диапазона от 0.5 до 17 ГГц форма объектов на глубине до 11 см восстанавливается с разрешением порядка 1 см.
Использование сверхширокополосного излучения и технологии радара с синтезированной апертурой даёт широкие возможности для разработки и применения различных методов постобработки данных измерений. Благодаря этому стало возможным создание алгоритмов наклонного или многоракурсного сканирования исследуемой среды. Разработанный алгоритм наклонной фокусировки также имеет высокое быстродействие.
Используя одни и те же данные радиозондирования и алгоритм наклонной фокусировки для различных углов, можно восстановить трёхмерную форму объекта, расположенного под поверхностью земли.
Предложен новый метод бесконтактного определения показателя преломления среды на основе метода радара с синтезированной апертурой не требующий априорной информации о глубине расположения рассеивающих объектов в среде. Приводятся результаты определения показателя преломления на численных моделях и результат применения предложенного метода для определения показателя преломления сухого песка в лабораторных условиях. Результат работы метода подтвержден измерениями временной задержки рассеянного сигнала в среде и априорной информацией о глубине залегания рассеивающих объектов. Для бесконтактного определения показателя преломления среды достаточно двух рассеивателей на различных глубинах либо одного точечного рассеивателя и чётко различимой ровной границей раздела сред.
Список литературы
1. Joaquim Fortuny-Guasch. A Novel 3-D Subsurface Radar Imaging Technique // IEEE Transactions on Geosciences and Remote Sensing. Vol. 40. No. 2, pp. 443-452, February 2002.
2. S. Valle,L. Zanzi, H. Lentz, H.M. Braun. Very high resolution radar imaging with a stepped frequency system // Eighth int. Conference on Ground Penetrating Radar, 2000, pp. 464-470.
3. Ivor L. Morrow and Piet van Genderen. Effective Imaging of Buried Dielectric Objects // IEEE Transactions on Geosciences and Remote Sensing. Vol. 40. No. 4, pp. 943-949, April 2002.
4. J. Groenenboom, A.G.Yarovoy. Data processing for a landmine detection dedicated GPR // In Eighth Intl. Conference on Ground Penetrating Radar, pp. 367-371, 2000.
5. A. H. Gunatllaka, B. A. Baertlein. A subspace decomposition technique to improve GPR imaging of anti-personnel mines // In Detection and Remediation Technologies for Mines and Minelike Targets V, pp. 1008-1018, 2000.
6. P. Meincke. Linear GPR Imaging Based on Electromagnetic Plane-Wave Spectra and Diffraction Tomography // Tenth International Conference on Ground Pene-trating Radar, 21-24 June, 2004, Delft, The Nether-lands. pp. 55-58.
7. Якубов В.П., Суханов Д.Я. Метод фокусировки в подповерхностной локации. //VII Международная научно-техническая конференция «Актуальные проблемы электронного приборостроения» АПЭП-2004, 21-24 сентября 2004. Новосибирск - С. 13-17.
8. V.P. Yakubov, A.S. Omar, V.P. Kutov, N.G. Spiliotis, D.Y. Suhanov. New Fast SAR Method for 3-D Subsurface Radiotomography // Tenth International Conference on Ground Pene-trating Radar, 21-24 June, 2004, Delft, The Nether-lands. pp. 103-106.
|
|
|