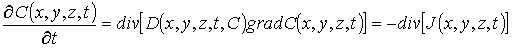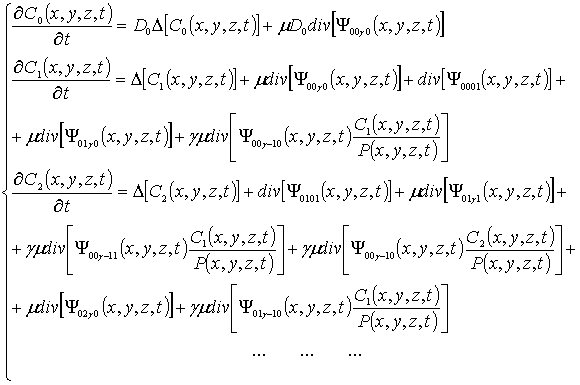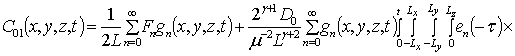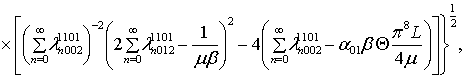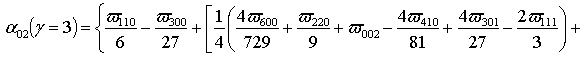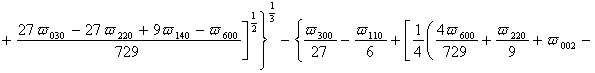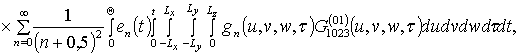УДК 539.219.3:669

ВЛИЯНИЕ НЕПОСТОЯНСТВА КОЭФФИЦИЕНТА ДИФФУЗИИ И РАСТВОРИМОСТИ ПРИМЕСИ В МНОГОСЛОЙНОЙ СТРУКТУРЕ НА РАСПРЕДЕЛЕНИЕ ПРИМЕСИ ПРИ ФОРМИРОВАНИИ В НЕЙ ДИФФУЗИОННОГО p-n-ПЕРЕХОДА. ОПТИМИЗАЦИЯ ДЛИТЕЛЬНОСТИ ОТЖИГА.

Е.Л. Панкратов
Институт физики микроструктур РАН, Нижний Новгород

Получена 21 февраля 2007 г.

С помощью предложенного в настоящей работе развития разработанной ранее методики анализа массо- и теплопереноса (см., например, [1,2]) проведен анализ динамики перераспределения примеси в многослойной полупроводниковой структуре с учетом временной и концентрационной зависимости коэффициента диффузии и растворимости примеси. Проиллюстрировано, что правильно выбранное пространственное распределение свойств твердотельной структуры позволяет увеличить резкость сформированного в ней диффузионного p-n-перехода, а также равномерность распределения примеси в обогащенной ею области. Обобщены полученные в [2] условия для одновременного увеличения резкости диффузионного p-n-перехода и равномерности распределения в нем примеси. Рассмотрена методика оптимизации длительности отжига для данных целей.
 

Введение

Необходимость увеличения быстродействия устройств полупроводниковой электроники, а также плотности элементов интегральных схем приводит к необходимости поиска материалов с более высокими скоростями переноса носителей и новых технологических методов производства электронных устройств. Одним из направлений повышения быстродействия полупроводниковых устройств является уменьшение емкостей электронно-дырочных переходов [3,4]. Большой интерес для увеличения надежности полупроводниковых устройств представляет увеличение однородности распределения примеси в легированных областях [3-5]. Актуальной задачей также является повышение точности теоретического описания технологических процессов, что приводит к повышению их предсказуемости и, как следствие, позволяет повышать воспроизводимость характеристик твердотельных устройств.

Для формирования p-n-переходов структур используются различные технологические методы (см., например, [4-6]), в том числе внедрение примеси в исходную пластину или эпитаксиальный слой (ЭС) путем ее диффузии, имплантации или в процессе выращивания ЭС. В настоящей работе рассматривается многослойная структура (МС) с пространственными размерами 2L_x´2L_y´L_z (см. рис.1), состоящая из подложки с размерами 2L_x´2L_y´L_z-a_z с коэффициентом диффузии D₃ и пределом растворимости P₃ и ЭС с пространственными размерами 2L_x´2L_y´a_z с коэффициентом диффузии D₂ и пределом растворимости P₂ который содержит участок с коэффициентом диффузии D₁ и пределом растворимости P₁. Данный участок для упрощения анализа выберем в виде параллелепипеда 2a_x´2a_y´a_z, а центр его поверхности 2a_x´2a_y примем за начало координат. Числовой множитель в пространственных масштабах по двум осям выбран для более компактной записи полученных в данной работе соотношений. Тип проводимости ЭС и подложки считается известным (n или p). В момент времени, принятый за начало отсчета, в участок ЭС с коэффициентом диффузии D₁ начинает поступать примесь, формирующая в нем второй тип проводимости (p или n).

Целью данной работы является поиск условий, при которых распределение концентрации внедряемой примеси будет наиболее равномерным в обогащенной ею области, а в остальной части МС примесь будет практически отсутствовать.

Методика анализа

Динамика перераспределения примеси в структуре ЭС – подложка описывалась вторым законом Фика в следующей форме

Рис. 1. Многослойная структура с двухматериальным

эпитаксиальным слоем
 

 

,    (1)

где  – пространственно-временное распределение примеси;  - пространственно-временное распределение потока примеси; div и grad – операторы соответственно дивергенции и градиента;  – коэффициент диффузии примеси в МС, величина которого зависит не только от динамических свойств примеси в материалах слоев МС, а также от быстроты изменения температуры МС во времени, но и от концентрации примеси. Концентрационная зависимость коэффициента диффузии может быть аппроксимирована следующим полиномом [5]: . Параметр  обычно принимает значения в интервале . Уравнение (1) необходимо дополнить граничными и начальными условиями. Граничное условие в окрестности начала координат, а также начальное условие зависят от вида источника примеси. В случае ограниченного источника они могут быть записаны в следующей форме
 

, , , .     (2а)
 

Начальное и первое граничное условия, соответствующие неограниченному источнику, имеют вид
 

, , , ,     (2б)
 

где  – приповерхностная концентрация примеси. Границ МС ,  и  примесь, как правило, не достигает (см., например, [3-5]). По этой причине второе граничное условие может быть рассмотрено как однородное условие первого рода
 

, , .                        (2с)
 

Для решения поставленной во введении цели определим решение уравнения (1) и воспользуемся им для анализа динамики перераспределения примеси. Для нахождения аналитического решения уравнения диффузии следуя работам [1,2] представим не зависящий от концентрации множитель аппроксимации коэффициента диффузии  в виде: , где , ,  - среднее значение коэффициента диффузии. Далее будем искать решение уравнения (1) в виде степенного ряда по параметру

.                             (3)

Функции  являются решением следующих систем уравнений

          (4)

где ,  - оператор Лапласа. Граничные и начальные условия для уравнений системы (4) имеют вид

, , ,

, , ,

при ограниченном источнике примеси и

, , ,

, , ,

при неограниченном источнике примеси.

Решение первого уравнения системы (4) определим с помощью метода осреднения функциональных поправок [7,8]. В рамках изложенного в [7,8] метода функция  во втором слагаемом правой части первого уравнения системы (4) заменяется в первом приближении ее средним значением

,

где  – первое приближение функции  по методу осреднения функциональных поправок, ,  - длительность диффузионного процесса. Далее полученное решение уточняется. Выбор более точной аппроксимации функции  в исходном приближении позволяет ускорить сходимость изложенной в [7,8] иттерационной процедуры. Может быть показано (см., например, [2,9]), что в предельном случае постоянного коэффициента диффузии (при быстром и слабом изменении коэффициента диффузии часто возможна аппроксимация его изменений средним значением  - см., например, [1]) распределение концентрации является односторонним гауссовым и может быть аппроксимировано суммой следующего ряда
 

,                             (5)

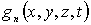
где , , , , ,  , , функция  описывает начальное распределение ограниченного источника примеси или перенесенный из граничного условия неограниченный источник примеси. Источник второго типа после переноса в уравнение (1) преобразуется к следующему виду . Подстановка соотношения (5) в первое уравнение системы (4) вместо функции  позволяет получить первое приближение данной функции в рамках рассматриваемого в настоящей работе развития метода осреднения функциональных поправок. Решение полученного уравнения стандартными методами (см., например, [9]) позволяет получить рассматриваемое приближение в окончательной форме

,

где .

Следующее приближение функции  по методу осреднения определим согласно изложенному в [7,8] алгоритму, т.е. заменой функции  во втором слагаемом первого уравнения системы (4) на сумму . Решение полученного уравнения может быть получено стандартными методами (см., например, [9]) и в окончательной форме имеет вид
 

,                            (6)

где
 
 , .

Параметр a₀₂ определяется с помощью следующего соотношения [7,8]

.                          (7)

Подстановка (6) в (7) позволяет получить соотношение для параметра a₀₂ в окончательном виде
 

,

где  
, , , , ,

где
, , , .

Первая и вторая функциональные поправки по параметру  к распределению концентрации примеси могут быть оценены аналогично исходному приближению , т.е. во втором и третьем уравнениях системы (4) функции  и  заменяются на распределение (5) во всех слагаемых начиная со второго. Решения таких уравнений, описывающих в рассматриваемом случае первые и вторые приближения функций  и  по методу осреднения функциональных поправок с ускоренной сходимостью, вынесены в приложение из-за их большого объема.

Показано, что второго приближения по параметру  достаточно для получения качественных и некоторых количественных выводов из анализа динамики перераспределения примеси [1,2]. Может быть также показано, что второго приближения по методу осреднения функциональных поправок также достаточно для получения аналогичных выводов. Использование численных методов позволяет провести такой анализ с большей точностью. Однако численные методы не обладают столь высокой наглядностью, как аналитические. По этой причине использовались и аналитические, и численные методы.

Результаты анализа

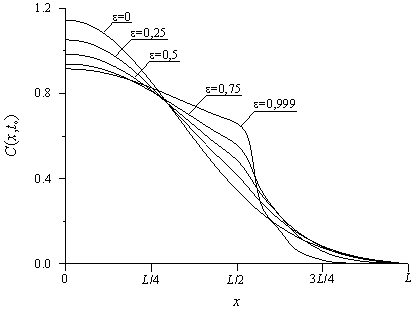
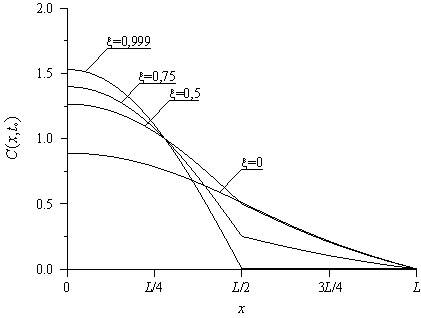
В первую очередь проведем анализ влияния пространственных изменений коэффициента диффузии и предела растворимости примеси на перераспределение примеси. Пространственное распределение примеси в фиксированный момент времени  приведено на рис. 2-4 для ограниченного источника и рис. 5-7 для неограниченного источника примеси при различных значениях параметров ,  и . Параметр  введен следующим образом: , , ,  - среднее значение предела растворимости примеси.

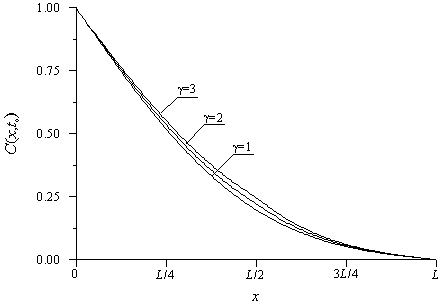
Из данных рисунков следует, что увеличение значений параметров ,  и  приводит к увеличению резкости p-n-перехода и равномерности распределения примеси в обогащенной примесью области. Следствием первого результата является уменьшение диффузионной емкости p-n-перехода. Следствием второго результата является снижение разогрева обогащенной примесью области в процессе протекания тока через p-n-переход при его фиксированной плотности или возможность уменьшения глубины p-n-перехода при фиксированной величине разогрева. Может быть показано, что увеличение скорости изменения коэффициента диффузии во времени позволяет увеличить резкость p-n-перехода. Однако, временная зависимость коэффициента диффузии не приводит к качественно новым результатам по сравнению с ранее известными. По этой причине она не будет рассматриваться.

Анализ изменения концентрации во времени показал, что при малой длительности диффузионного процесса примесь не достигает границы раздела между слоями МС. В таком случае не удается использовать полуотражающее свойство границы раздела между слоями МС для улучшения свойств p-n-перехода. При большой длительности диффузионного процесса распределение примеси становится слишком равномерным и использовать полуотражающее свойство границы раздела между слоями МС для улучшения свойств p-n-перехода также практически не удается. По этой причине необходим выбор компромиссной длительности отжига: с одной стороны примесь должна достичь границы раздела, с другой стороны она
 

Рис.2. Пространственное распределение примеси, поступающей из ограниченного источника, в фиксированный момент времени , при различных значениях параметра , ,  и ,
 

Рис.3. Пространственное распределение примеси, поступающей из ограниченного источника, в фиксированный момент времени , при различных значениях параметра , ,  и
 

Рис.4. Пространственное распределение примеси, поступающей из ограниченного источника, в фиксированный момент времени , при различных значениях параметра , ,  и
 

Рис.5. Пространственное распределение примеси, поступающей из ограниченного источника, в фиксированный момент времени , при различных значениях параметра , ,  и
 

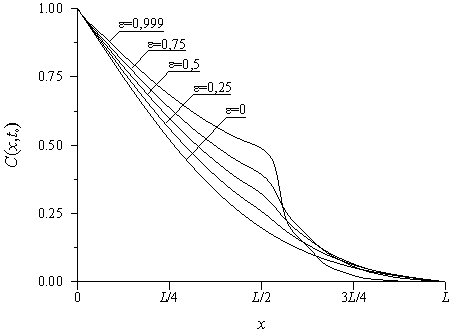
Рис.6. Пространственное распределение примеси, поступающей из неограниченного источника, в фиксированный момент времени , при различных значениях параметра , ,  и
 

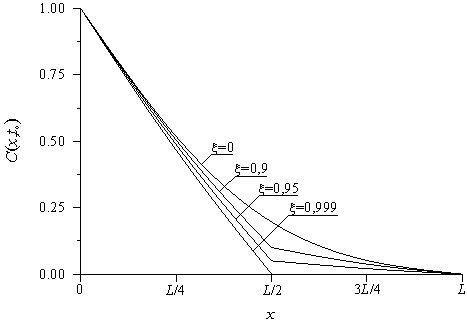
Рис.7. Пространственное распределение примеси, поступающей из неограниченного источника, в фиксированный момент времени , при различных значениях параметра , ,  и
 

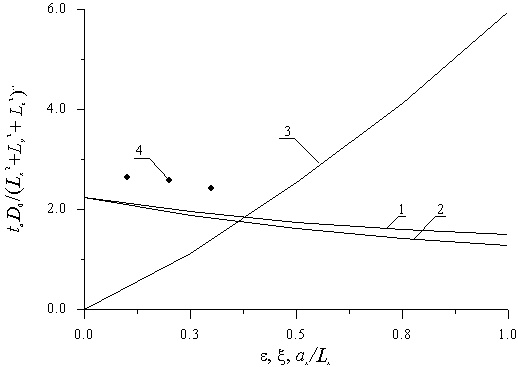
не должна проникать слишком далеко. Для оценки компромиссного времени отжига может быть использовано несколько критериев [2]. В рамках первого из них компромиссное время отжига определяется как время, за которое концентрация примеси уменьшается на 3 дБ от своего максимального значения к границе раздела между материалами МС. В рамках второго критерия компромиссное время отжига определяется из условия минимума среднеквадратического отклонения реального распределения примеси от некоторого требуемого профиля C(x,t₀)=M[1(x)-1(x-x₀)] [2], что позволяет называть его оптимальным. Ранее было показано, что максимальная разница между значениями компромиссного времени отжига, полученными в рамках различных критериев, составляет около 30%. Типичные зависимости компромиссного времени отжига от различных параметров приведены на рис. 8 и 9.
 

Рис.8. Зависимость компромиссного времени отжига примеси, поступающей из ограниченного источника, от величины парамет-ра  (кривая 1) при  и , ;  при  и  (кривая 2); отношения  при ,  и  (кривая 3) и  при ,  и
 

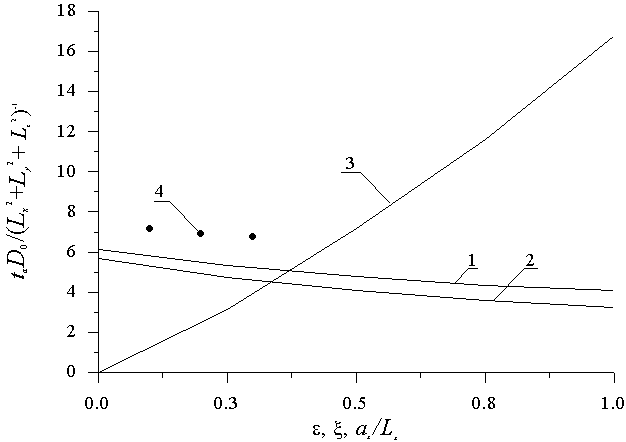
Рис.9. Зависимость компромиссного времени отжига примеси, поступающей из неограниченного источника, от величины параметра  (кривая 1) при  и , ;  при  и  (кривая 2); отношения  при ,  и  (кривая 3) и  при ,  и

 

 

Из последних рисунков следует, что компромиссное время отжига убывает с ростом безразмерных величин отклонения коэффициента диффузии и предела растворимости от средних значений (соответственно  и ) и увеличивается с ростом объема области ЭС с коэффициентом диффузии  и растворимостью . Таким образом, увеличение разницы в свойствах различных участков МС и уменьшение толщины ЭС позволяет уменьшить длительность отжига примеси при формировании p-n-перехода, что позволяет при высокотемпературном отжиге уменьшить перемешивание слоев МС и, как следствие, максимально сохранить резкость соответствующих границ раздела.

Заключение

В настоящей работе проведен анализ динамики примеси в многослойной структуре в процессе формирования p-n-перехода в окрестности границ раздела между слоями. Анализ проводился с учетом пространственных изменений коэффициента диффузии и растворимости примеси, а также с учетом временной и концентрационной зависимости коэффициента диффузии. Показано, что правильно выбранное различие в свойствах слоев многослойной структуры позволяет увеличить резкость p-n-перехода и равномерность распределения примеси в обогащенной ею области. Такой выбор также позволяет уменьшить оптимальное время отжига примеси, соответствующее максимуму компромисса между увеличением равномерности распределения примеси в обогащенной ею области и резкостью p-n-перехода. В настоящей работе также предложено развитие разработанного ранее метода осреднения функциональных поправок, позволяющее ускорить его сходимость.

Приложение

Первое приближение функциональной поправки

Второе приближение функциональной поправки

Параметр , определяемый с помощью аналогичного (7) соотношения, в окончательной форме имеет вид

Первое приближение функциональной поправки

Второе приближение функциональной поправки

.

Параметр  определяемый с помощью аналогичного (7) соотношения, в окончательной форме имеет вид

 

Литература

[1] Е.Л. Панкратов. // Известия вузов. Прикладная нелинейная динамика. - 2004. - Т.12, №3. - С. 35-44.

[2] E.L. Pankratov // Phys. Rev. B. 2005. V.72, №7. P. 075201-075208.

[3] В.Г. Гусев, Ю.М. Гусев. Электроника. М.: Высшая школа, 1991. 622с.

[4] A.B. Grebene. Bipolar and MOS analogous integrated circuit design. New York, John Wyley and Sons, 1983, 894 p.

[5] З.Ю. Готра. Технология микроэлектронных устройств. - М.: Радио и связь. 1991. 528с.

[6] T. Ahlgren, J. Likonen, J. Slotte, J. Raisanen, M. Rajatore, J. Keinonen // Phys. Rev B. 1997. V.56, №8. P. 4597-4603.

[7] Ю.Д. Соколов // Прикладная механика. 1955. Т.1. С. 23-35.

[8] А.Ю. Лучка. Теория и применение метода осреднения функциональных поправок. – Киев: Издательство АН УССР. 1963. 128 с.

[9] А.Н. Тихонов, А.А. Самарский. Уравнения математической физики. - М.: Наука. 1972. 735 с.

xxx