УДК 004.932.2
СРАВНИТЕЛЬНОЕ ИССЛЕДОВАНИЕ СПОСОБОВ ОЦЕНКИ ФОНА В ВИДЕОПОСЛЕДОВАТЕЛЬНОСТЯХ
С. А. Кузьмин
Санкт-Петербургский государственный университет аэрокосмического
приборостроения, факультет
радиотехники, электроники и связи, кафедра электронных и телевизионных
систем
Аннотация. Исследованы модели статистического представления исходных и разностных видеокадров как смеси распределений. Показано, что отличие значений среднеквадратических отклонений гистограмм разностных изображений может быть интерпретировано как следствие различных условий наблюдения некоего эталонного разностного изображения, что позволяет априорно оценить характеристики алгоритмов выделения. В ходе эксперимента проведено сравнение алгоритмов оценки фона.
Ключевые слова: вычитание оценки фона, оценка фона, межкадровая разница, смесь распределений, отношение сигнал-шум.
Abstarct: In first part of article models of statistical presentation of several types of images as mixture of distributions are studied. In the second part of the article the difference between MSE values for histograms of difference images is interpreted as difference in conditions of acquisition of etalon difference images that gives an ability to a priori make a conclusion on characteristics of object detection algorithm. Final part consists of experimental comparison of several background estimation algorithms.
Keywords: background subtraction, background estimation, inter-frame difference, mixture of distributions, signal-to-noise ratio.
Введение
Задача выделения объектов по видеопоследовательностям возникает во многих практических применениях. Под выделением объектов в рамках данной статьи понимается процедура разделения областей кадра по семантическому значению с целью сортировки на более и менее семантически значимые. Это определение сделано для контраста с определением сегментации – процедурой разделения изображения на области по яркости или иным низкоуровневым признакам. Результат сегментации совпадает с результатом выделения только, если объекты однородно окрашены по всей своей площади, т.е. не составлены из частей разных цветов и яркостей (рис.1).

Рис.1. Пример работы фильтра предварительной обработки перед сегментацией кадра. Результат последующей сегментации будет семантически неправильным.
Для теоретического анализа отобран узкий круг подходов к выделению, который может быть по аналогии применен к другим подходам. Во второй части теоретически исследуются возможности обнаружения объекта по одному кадру, по двум кадрам, по трем кадрам, по набору кадров на основании анализа характеристик гистограмм яркости (гистограмм изображений разности кадров при количестве кадров больше двух) изображений. В третьей части практически исследуются возможности обнаружения объекта по двум кадрам и по набору кадров.
Модели статистического представления исходных и разностных видеокадров как смеси распределений
В задаче выделения пикселям более семантически значимых объектов обычно присваивают белый цвет, а пикселям менее значимых – черный. Это дает возможность на последующих этапах представлять изображение меньшим количество битов и ускоряет загрузку изображений в память, что важно во встраиваемых системах. Процесс перевода изображения из полутонового или цветного представления в черно-белый формат сводится к присваиванию пикселям черного или белого цвета в зависимости от яркости исходных изображений или некоторых вычисленных признаков (разностные кадры, контуры и т.п.). Принятое решение для пикселя может оказаться ложным, если входное изображение (или его препарат) низкого качества или если количество семантически значимых компонентов в смеси распределений гистограммы входного изображения N≥2. Отметим, что различные шумы в статье полагаются аддитивными с нулевым средним значением и сравнительно небольшой дисперсией и не показаны на графиках как отдельный компонент, т.к. лишь приводят к расширению других распределений.
Рассмотрим гистограммы изображений для того, чтобы понять какие способы выделения лучше, а какие хуже подходят для практических задач именно по количеству компонент в смеси входного кадра. Модели смеси распределений для разного количества учитываемых кадров:
1. для одного кадра:
1.1. самой простой статистической моделью кадра с объектами будет смесь «B+O» из двух распределений – фона B и объекта O (рис.2). Для этой модели есть вариант без ошибок выделения (рис.2-А) и вариант с ошибками выделения (рис.2-B). Красным цветом показан порог бинаризации – процедуры перевода многобитного изображения в однобитное.
1.2. более реалистичная модель [1] представляет из себя смесь «S+O1+B1+O2+B2» из 5 распределений – теней S, темного объекта O1, темного фона B1, светлого объекта O2, светлого фона B2 (рис.3).
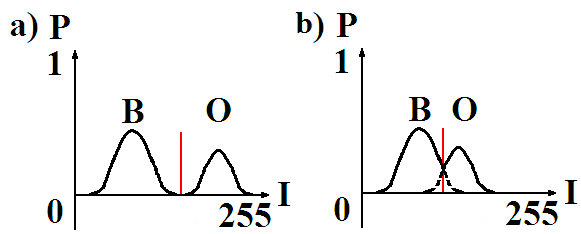
Рис. 2. Двухкомпонентные
модели смеси распределений для 1 кадра.
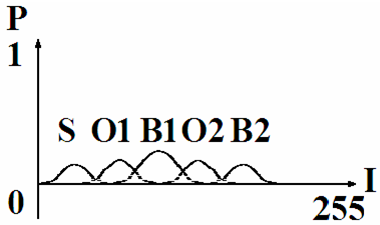
Рис. 3. Пятикомпонентная модель смеси распределений для 1 кадра.
В случае 5 компонентов в смеси распределений выбор любого порога приведет к ошибкам выделения в ходе бинаризации – либо не будет выделена часть объекта, либо будет выделена часть фона. Эта пятикомпонентная модель будет использоваться в дальнейшем;
2. для двух кадров:
2.1. при наличии двух кадров (текущего и предыдущего) может вычисляться межкадровая разница (как вариант межкадровая поблочная разница), вычисленная бинаризованная межкадровая разница может объединяться с бинаризованным контурным препаратом текущего кадра. Объединение может происходить с помощью логической операции AND [2] или Moving-Edge Closure [3]. При межкадровой разнице смесь распределений может содержать до 21 компонента, которые сведены в табл.1;
Таблица 1. Компоненты смеси распределений для изображения межкадровой разницы
|
s(t)-s(t-1) |
s(t)-o1(t-1) |
s(t)-b1(t-1) |
s(t)-o2(t-1) |
s(t)-b2(t-1) |
|
o1(t)-s(t-1) |
o1(t)-o1(t-1) |
o1(t)-b1(t-1) |
o1(t)-o2(t-1) |
o1(t)-b2(t-1) |
|
b1(t)-s(t-1) |
b1(t)-o1(t-1) |
b1(t)-o2(t-1) |
|
|
|
o2(t)-s(t-1) |
o2(t)-o1(t-1) |
o2(t)-b1(t-1) |
o2(t)-o2(t-1) |
o2(t)-b2(t-1) |
|
b2(t)-s(t-1) |
b2(t)-o1(t-1) |
b2(t)-o2(t-1) |
|
|
2.2. если второй кадр представляет собой изображение в отсутствии объектов и теней, или является рассчитанной оценкой фоновой составляющей, то его модель «B1+B2» содержит всего 2 компонента оценок темного B1 и светлого фона B2. Они более узкие (в случае оценивания фона производится низкочастотная фильтрация) и высокие (рис.4);
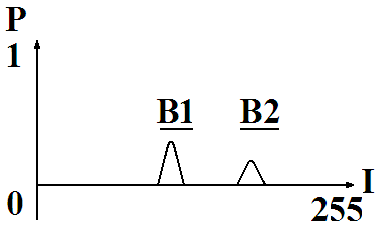
Рис. 4. Смесь распределений для изображения оценки фона.
Модель изображения разности кадра и фона (или оценки фона) содержит 8 компонентов: s(t)-b1(t), s(t)-b2(t), o1(t)-b1(t), o1(t)-b2(t), b1(t)-b1(t), o2(t)-b1(t), o2(t)-b2(t), b2(t)-b2(t).
3. для трех кадров способ выделения предложен в статье [4] и заключается в том, что вычисляются бинаризованные межкадровые разницы (I(T)-(I(T-1)) и (I(T-1)-(I(T-2)), которые объединяются с помощью операции AND. Модели кадра такие же, как в табл.1.
4. для набора кадров:
4.1. может вычисляться т.н. многомасштабная межкадровая разница [5] не между соседними кадрами, а между кадрами, отстоящими друг от друга на больший отрезок времени – это актуально в случае медленно движущихся объектов. Модель кадра такая же, как в табл.1.
4.2. может производиться оценка фона с помощью попиксельной фильтрации в направлении оси времени. Подходов очень много – различные варианты взвешенного усреднения, вычисления порядковой статистики (минимальной, медианной, максимальной яркости), статистических характеристик гистограмм распределения яркости (моды), моделирования участков фона с помощью метода главных компонент[6]. Модель кадра такая же, как в 2.2.
Различие между алгоритмами межкадровой разницы и алгоритмами вычитания оценки фона заключается в том, что: 1) алгоритмы оценки фона обычно используют фильтрацию несколько десятков кадров для получения приемлемой оценки фона, в то время как межкадровая разница по сути является тем же самым, но только в качестве изображения оценки фона используется предыдущий кадр; 2) в предыдущем кадре объекты находятся почти на тех же самых позициях, что и в текущем. Это ведет к ослаблению полезного сигнала для однородно окрашенных объектов в отличие от алгоритмов оценки фона, в которых полезный сигнал на значительной площади объекта вычитается не сам из себя, а из фона.
Сравнение характеристик гистограмм разностных изображений как способ априорной оценки характеристик алгоритма выделения
Рассмотрим гистограммы распределения яркости в изображениях межкадровой разности и разности кадра и оценки фона (рис. 5-6). Как внешний вид гистограмм, так и значения среднеквадратического отклонения (СКО) этих гистограмм отличаются: гистограмма яркостей межкадровой разницы узкая и высокая, а гистограмма яркостей разницы кадра и фона низкая и широкая. При этом участки высокой яркости в разностных изображениях соответствуют участкам объекта, а средние значения распределений в гистограммах равны нулю.
Для этого случая СКО распределения разностного изображения совпадает с его среднеквадратическим значением, т.е. амплитуда полезного сигнала определяется величиной СКО:
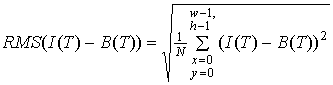 ,
,
 ,
,
RMS(I(T)-B(T))=MSE(I(T)-B(T)) при M(I(T)-B(T))=0, где M(I(T)-B(T)) – среднее значение яркости в гистограмме.
Для изображения межкадровой разности расчеты аналогичные. Поскольку раньше было сказано, что шум аддитивный с нулевым средним, то и для него среднеквадратическое значение также совпадает с СКО.
Если отличие внешнего вида разностных изображений интерпретировать как различие в условиях наблюдения некоего эталонного разностного изображения, то есть при разном отношении сигнал-шум, то на изображении с большим значением сигнал-шум объекты будет выделяться более точно по сравнению с худшим изображением, для которого будут большие значения вероятностей ложной тревоги и ложных пропусков.

Рис. 5. Гистограмма изображения
межкадровой разности. СКО=12,36.

Рис. 6.
Гистограмма изображения межкадровой разности. СКО=16,15.
Формула вычисления отношения
сигнал-шум по амплитуде для протяженного сложного сигнала без ярко выраженного
максимума [7]  .
.
В данном случае 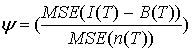 , где n(T) – СКО шума на
разностном изображении. В децибелах отношение сигнал-шум выглядит так
, где n(T) – СКО шума на
разностном изображении. В децибелах отношение сигнал-шум выглядит так  .
.
Если характеристики
камеры неизвестны, то значение СКО шума n(T) можно получить,
вычислив его на фоновом участке изображения (без объектов и теней), т.к. там
единственным источником ненулевой разницы будут шумы (шум квантования, ошибки в
оценке фона из-за изменения освещенности). Если характеристики камеры известны
(типичные значения отношения сигнал-шум современных камер около 46 дБ), то
можно вычислить СКО шума 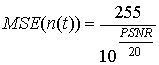 .
.
Для оценки априорного
превосходства алгоритма выделения (преимуществ, предоставленных лучшими
условиями наблюдения) при использовании разных алгоритмов получения
разностного изображения можно использовать разность вычисляемых значений
сигнал-шум ![]() .
.
Полагая ![]() из-за того, что разные алгоритмы оценки
фона тестируются на одних и тех же кадрах, получим
из-за того, что разные алгоритмы оценки
фона тестируются на одних и тех же кадрах, получим
 ,
,
где ![]() ,
, ![]() – СКО
распределений яркости разностных изображений (до взятия абсолютного значения)
при разных алгоритмах оценки фона.
– СКО
распределений яркости разностных изображений (до взятия абсолютного значения)
при разных алгоритмах оценки фона.
Более грубую оценку можно
получить, вычисляя только числитель дроби – разности СКО разностных изображений
![]() . Стоит отметить, что грубая версия будет
давать немного заниженные априорные оценки для алгоритмов вычитания оценок
фонового изображения, построенных по набору кадров по сравнению с алгоритмами
межкадровой разницы, т.к. в изображениях, полученных по алгоритмам оценки фона уровень
шума становится меньше из-за низкочастотной фильтрации.
. Стоит отметить, что грубая версия будет
давать немного заниженные априорные оценки для алгоритмов вычитания оценок
фонового изображения, построенных по набору кадров по сравнению с алгоритмами
межкадровой разницы, т.к. в изображениях, полученных по алгоритмам оценки фона уровень
шума становится меньше из-за низкочастотной фильтрации.
Если вычислять отношение сигнал-шум в децибелах, то знать СКО шума не нужно, т.к. он одинаков для сравниваемых изображений и при вычислениях исключается из рассмотрения:
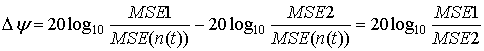 .
.
Методика эксперимента и полученные результаты
В ходе эксперимента проведено сравнение нескольких алгоритмов оценки фона. Для тестирования использовалось 4 клипа (England, car flow, highway, Module), из каждого клипа брались отрезки по 100 кадров, для которых производилась оценка фона и вычислялись разностные изображения.
На рис. 7-8 показаны примеры кадров клипов и полученных изображений оценок фона.
Исследовались следующие алгоритмы оценки фона:
1) межкадровая разница (для клипов 3 и 4 эффект оказался похож на многомасштабную межкадровую разницу из-за высокой скорости движения объектов);
2) попиксельное вычисление медианы в направлении оси времени (в.н.о.в.);
3) попиксельное вычисление моды в.н.о.в.;
4) попиксельное вычисление средней яркости в.н.о.в.;
5) попиксельное вычисление оценки яркости на основе фильтра Калмана в.н.о.в.
Изображения оценок фона, полученных разными алгоритмами, похожи на большей площади изображения и отличия могут быть только в зонах движения объектов.

Рис.7.
Примеры текущих кадров клипов (верхний ряд - England, car flow, нижний ряд -
highway, Module).
Данные априорной оценки алгоритмов приведены в таблицах 2-4 по каналам R, G, B. Жирным шрифтом отмечены сильнейшие алгоритмы.
Таблица 2. Данные априорной оценки алгоритмов по величинам СКО - канал R
|
Название метода/ клип |
Клип 1
|
Клип 2
|
Клип 3
|
Клип 4
|
|
Межкадровая разность/ММКР |
10,194 |
15,977 |
24,04 |
17,806 |
|
Среднее |
11,988 |
21,969 |
23,434 |
16,713 |
|
Калман |
12,091 |
22,342 |
23,671 |
16,838 |
|
Медиана |
12,093 |
22,738 |
26,291 |
17,136 |
|
Мода |
12,141 |
23,248 |
26,805 |
17,456 |
|
|
1,51 |
3,25 |
1,16 |
0,55 |

Рис. 8. Полученные изображения оценок фона с помощью фильтра Калмана с растущей памятью.
Таблица 3. Данные априорной оценки алгоритмов по величинам СКО - канал G
|
Название метода/ клип |
Клип 1
|
Клип 2
|
Клип 3
|
Клип 4
|
|
Межкадровая разность/ММКР |
8,8881 |
15,466 |
23,691 |
17,402 |
|
Среднее |
17,426 |
20,95 |
22,978 |
17,008 |
|
Калман |
17,589 |
21,298 |
23,212 |
17,103 |
|
Медиана |
17,599 |
21,531 |
25,863 |
17,072 |
|
Мода |
17,636 |
22 |
26,35 |
17,324 |
|
|
5,95 |
3,06 |
0,92 |
0,20 |
Таблица 4. Данные априорной оценки алгоритмов по величинам СКО - канал B
|
Название метода/ клип |
Клип 1
|
Клип 2
|
Клип 3
|
Клип 4
|
|
Межкадровая разность/ММКР |
9,1396 |
16,27 |
23,37 |
18,21 |
|
Среднее |
16,04 |
22,053 |
22,7 |
17,278 |
|
Калман |
16,2 |
22,403 |
22,948 |
17,389 |
|
Медиана |
16,208 |
22,521 |
25,451 |
17,353 |
|
Мода |
16,27 |
23,01 |
25,943 |
17,806 |
|
|
5 |
3,01 |
1,16 |
0,45 |
Анализ таблиц 2-4 показывает, что превосходство сильнейшего алгоритма по величине СКО относительно слабейшего незначительно среди алгоритмов оценки фона, но при сравнении межкадровой разницы в клипах 1-2 и алгоритмов оценки фона видно, что в среднем превосходство оценок фона составляет 3-5 дБ, что является существенным отличием. Для отдельных кадров превосходство может достигать и 10 дБ (величины СКО 28 и 8 для оценки фона и межкадровой разницы соответственно). Среди исследованных алгоритмов оценок фона наилучшие результаты показал алгоритм попиксельного вычисления моды в направлении оси времени.
Выводы:
1. чем больше компонентов в смеси распределений, тем хуже характеристики алгоритма выделения. Ошибки выделения появляются при количестве семантически значимых компонентов смеси распределений N≥2;
2. различие значений среднеквадратических отклонений гистограмм разностных изображений, полученных для разных алгоритмов оценки фона, позволяет априорно оценить характеристики алгоритмов выделения – чем меньше СКО гистограммы распределения яркостей в разностном изображении, тем хуже характеристики алгоритма выделения, который будет использовать это изображение;
3. чем меньше отрезок времени, за который вычисляется оценка фона, тем точнее она будет «аппроксимировать» яркость фоновой составляющей в местах кадра, где нет объектов. При увеличении времени оценивания дисперсия гистограммы распределения яркости меняется (в основном растет), т.к. корреляция значений яркости во времени уменьшается как из-за изменений освещенности, так и из-за движения объектов;
4. по результатам исследований попиксельное вычисление моды в направлении оси времени дает наилучшие оценки фона. На участках кадра, где движутся объекты, для корректной оценки желательно, чтобы в клипе для каждого пикселя c координатами [x,y] количество кадров без объектов в нем было больше количества кадров с объектами в нем;
5. межкадровая и многомасштабная межкадровые разницы имеют следующие недостатки: удлинение объекта на величину смещения за время кадра при его высокой текстурированности (неоднородности окраски) или пропадание однородно окрашенных протяженных участков объекта (вычитание из самого себя) при низкой текстурированности. Удлинение объекта ведет к увеличению СКО, которое может даже превосходить СКО для методов оценки фона;
6. при выделении семантически значимых объектов из цветных изображений надо отдать приоритет каналу с наибольшей разницей СКО гистограмм разностных сигналов.
Литература
1. Кузьмин С. А. Анализ и сжатие видеоинформации в условиях наблюдения объектов на статическом фоне// Труды 7-ой международной конференции «Телевидение: передача и обработка изображений», СПб, 2009. С. 146-150.
2. Vieren C., Cabestaing F., and Postaire J.G., Catching Moving Objects with Snakes for Motion Tracking. Pattern Recognition Letters, Vol. 16, No. 7, July 1995, pp. 679-685.
3. Cucchiara R., Piccardi M., Prati A., Scarabottolo N., Real-time Detection of Moving Vehicles// Proceedings of 10th International Conference on Image Analysis and Processing(ICIAP 99), Venice, Italy, Sept. 1999. Pp. 618-623.
4. Kameda Y., Minoh M. A human motion estimation method using 3-successive video frames// Proc. Of International Conference on Virtual systems and multimedia, Japan, Gifu, 1996. Pp. 135-140.
5. Обухова Н.А. Методы видеонаблюдения, сегментации и сопровождения движущихся объектов: автореф. дис. ... доктора техн. наук: 05.12.04: защищена 05.11.2008/ Н.А. Обухова; СПбГЭТУ «ЛЭТИ». – СПб, 2008. – 34 с.
6. Афанасенко А.С. Отображение и определение параметров протяженных объектов при телевизионном наблюдении: автореф. дис. ... канд. техн. наук: 05.13.01: защищена 19.05.2009/ А.С. Афанасенко; ГУАП. – СПб, 2009. – 19 с.
7. Рабинович Е.В. Методы и средства обработки сигналов: Учебное пособие. – Новосибирск: НГТУ, 2008. – 120 с.