ОЦЕНКА РЕАЛИЗАЦИИ СВОЙСТВА СВЕРХШИРОКОПОЛОСНОСТИ Т-ВОЛН ДЛЯ АНТЕНН ПОДПОВЕРХНОСТНОГО ЗОНДИРОВАНИЯ С ПАРАМЕТРИЧЕСКОЙ ОПТИМИЗАЦИЕЙ РАЗМЕРОВ ПОПЕРЕЧНЫХ СЕЧЕНИЙ ТОКОВЕДУЩИХ ЛИНИЙ
В. Б. Болтинцев
ЗАО НПФ «Геодизонд»
Получена 5 марта 2012 г.
Аннотация. Путём параметрической оптимизации размеров поперечных сечений токоведущих линий антенны бегущей волны получена развязка её погонной индуктивности с подстилающей средой. Приведены параметры антенны, измеренные относительно сухого бетона. Неравномерность S-параметров матрицы рассеяния (<8.5%) в диапазоне частот 0.3-700 МГц позволяет оценить сверхширокополосность антенны как характерную для Т- волн.
Ключевые слова: сверхширокополосные антенны; георадиолокация; микрополосковая линия; антенна бегущей волны; уравнение антенны подповерхностного зондирования; характеристическое сопротивление.
Abstract. The junction of the inductance of the traveling wave antenna with the underlying environment was received with the parametric optimization of cross-sectional dimensions of current-carrying lines of this traveling wave antenna. The equation of the subsurface sensing antenna is given. The parameters of the antenna measured relative to the dry concrete are also given. Irregularity of the S-parameters of the matrix (< 8.5 %) in d. ch. 0.3-700 MHz allows to evaluate UWB antenna as a characteristic of T-waves.
Keywords: UWB antenna; georadar; microstrip line; traveling-wave antenna; the antenna equation subsurface sensing; characteristic impedance.
Введение
За последние годы значительно возрос интерес к методам и устройствам подповерхностной радиолокации и зондирования подстилающих сред, а также георадиолокации. К настоящему времени различными разработчиками создано значительное количество off-the-shelf устройств для ряда технических приложений. При этом, однако, остаются нерешёнными вопросы теории, дизайна и практических приложений некоторых классов приборов подобного типа.
Впервые радиоотражение от подповерхностных структур было случайно зафиксировано радиолокационным высотомером на ледовом аэродроме в Антарктиде А. Уэйтом в 1957 г. Он обратил внимание на то, что радиовысотомер показывал высоту 900 футов еще до момента отрыва самолета от взлетной полосы. Оказалось, что радиовысотомер, который представлял собой импульсный радиолокатор, фиксировал отражение от нижней границы ледника. Это послужило началом исследований вопроса об использовании радиолокации в геофизике.
Позже выяснилось, что применение обычных схем радиолокаторов для целей
подповерхностного зондирования возможно только в ограниченном количестве
случаев, когда затухание радиоволн в среде мало (лёд, сухие песчаники, каменная
соль и т.п.). Для подавляющего большинства водонасыщенных пород, когда
затухание радиоволн весьма велико, необходимы иные технические решения.
История вопроса и проблематика исследований
Для увеличения разрешения и энергетического потенциала предпринимались попытки использовать широкополосные сигналы с линейной частотной модуляцией или шумоподобные с фазовой модуляцией, в основном так и оставшиеся на стадии эксперимента. Для получения положительного результата база такого сигнала должна была быть меньше расстояния между отражающими границами. Такое условие для подстилающей среды практически никогда не выполняется (за исключением, возможно, зондирования льда), поэтому применение широкополосных сигналов с последующей их корреляционной обработкой приводит к плохому разрешению соседних сигналов на фоне боковых лепестков корреляционной функции зондирующего сигнала.
Выход из положения был найден в применении импульса без несущей, который представляет собой одно или несколько колебаний ВЧ тока в антенне и имеет в пределе бесконечную полосу частот. Для регистрации сигналов в первых конструкциях георадаров обычно использовался стробоскопический осциллограф, при этом амплитуда сигнала на кристаллическом диоде на входе стробоскопического осциллографа не должна была превышать 1 В [1].
Реально георадиолокация начинает свою историю с 1960 г., когда переход на предложенный И. Куком зондирующий импульс без несущей частоты позволил создать прибор, способный работать не только на ледниках, но и в других средах. В нашей стране начало подобных работ положено М. И. Финкельштейном (1976). Только сегодня осознаются огромные возможности георадиолокации.
Способ формирования импульса без несущей получил название «метод ударного возбуждения антенны»: на передающую антенну тем или иным образом подается скачок напряжения, который в антенне преобразуется в излучаемый СШП сигнал. Существующие модели георадаров различаются типом решаемых задач, видом используемого сигнала, обработкой (способом идентификации) и т. д. Выбор характеристик излучаемых импульсов с напряжениями до 300 В и токами в антенне до 1 А привели к созданию информационно – измерительных систем (ИИС) типа Penetrating Radar System (PRS), или аналогичных им Ground Penetrating Radar (GPR).
В свою очередь, использование импульсов с амплитудой до 104 В и токами порядка 100 А дает возможность создать сверхширокополосные (СШП) ИИС с большим динамическим диапазоном входного сигнала (1 мВ – 100 В) и антеннами, в которых становится возможным согласование со средой по волновому сопротивлению.
Сегодня подавляющее большинство рынка георадаров составляют ИИС с относительно
маломощными генераторами (амплитуда импульса ![]() ),
приёмником с прямым стробоскопическим преобразованием и антеннами типа «диполь Герца»
или его разновидностями. К сожалению, всем георадарам класса PRS или GPR свойственно слабое метрологическое обеспечение
[2], поскольку ключевую роль в них
играют антенны, чья сверхширокополосность, растянутая в область высоких частот,
в ряде случаев является мешающей для результата измерений. Последнее
обусловлено тем, что ВЧ составляющая сигнала в подстилающей среде затухает
очень быстро и избыточная полоса приёмника забивается шумом (отношение
«сигнал/шум» резко падает).
),
приёмником с прямым стробоскопическим преобразованием и антеннами типа «диполь Герца»
или его разновидностями. К сожалению, всем георадарам класса PRS или GPR свойственно слабое метрологическое обеспечение
[2], поскольку ключевую роль в них
играют антенны, чья сверхширокополосность, растянутая в область высоких частот,
в ряде случаев является мешающей для результата измерений. Последнее
обусловлено тем, что ВЧ составляющая сигнала в подстилающей среде затухает
очень быстро и избыточная полоса приёмника забивается шумом (отношение
«сигнал/шум» резко падает).
Основными элементами конструкции любого георадара являются антенны, поскольку они определяют полосу исследуемого процесса. Как правило, они должны быть демпфированными (резистивно – нагруженными) диполями (антенны Ву-Кинга), поскольку без дополнительного искусственного демпфирования на большинстве водонасыщенных почв антенны недопустимо долго «звенят» - излучаемые волны резонируют между антенной и подповерхностной средой из-за несоблюдения условий согласования. Но применение демпфирования снижает энергетический потенциал георадара, а значит, и максимальную глубину исследований.
Оптимальный частотный диапазон антенн для подповерхностного локатора всегда является компромиссом, с одной стороны, между глубиной зондирования (1÷100 м и более) [3] и разрешением (1÷10 см) в зависимости от решаемой задачи для реальных геологических структур, с другой стороны – между частотными свойствами антенны (измеренными относительно импедансной подстилающей среды с известными характеристиками) и её габаритами.
Первые промышленные образцы СШП антенн (измерительные антенны П6-23, аттестованные в полосе 1…18 ГГц «по воздуху») с метрологически аттестованными характеристиками были созданы в СССР к середине 1970-х годов, хотя первая публикация (Черноусов В. С.) относится к 1965 г.
Первый комплекс на базе ЛБВ в качестве передатчика и стробоскопического осциллографа С1-91/4 в качестве приёмника был создан в ВИКИ им. А. Ф. Можайского (конец 1970-х). В качестве антенн использовались диполи Герца. Запись сигнала осуществлялась на микро-ЭВМ «Электроника».
Во втором комплексе (~ 1987 г.) передатчиком выступал генератор на базе дрейфового
диода с резким восстановлением обратного напряжения (ДДРВ, 1985 г, Физико-технический институт им. А. Ф. Иоффе)
[4]
с амплитудой тока в импульсе ![]() и стробоскопический
осциллограф С9-9 – в качестве приёмника. Запись сигнала осуществлялась на ЭВМ
«СМ-4».
и стробоскопический
осциллограф С9-9 – в качестве приёмника. Запись сигнала осуществлялась на ЭВМ
«СМ-4».
В этом комплексе использовался метод разнесённых приемной и передающей антенн (измерительные антенны П6-23). Оба комплекса имели указанное выше ограничение по уровню входного сигнала.
Опыт работ по прецизионному измерению СШП радиолокационных характеристик,
а также появление промышленной антенны П6-33, аттестованной в полосе 80…1000
МГц «по воздуху», и цифрового осциллографа С9-28 (ограничение по входу ![]() ), способного записать сигнал на PC-XT, с учётом уже существующих генераторов на базе ДДРВ
позволили осуществить первые работы по исследованию подповерхностной среды (1991)
[5].
), способного записать сигнал на PC-XT, с учётом уже существующих генераторов на базе ДДРВ
позволили осуществить первые работы по исследованию подповерхностной среды (1991)
[5].
Это послужило толчком к дальнейшему развитию и совершенствованию метода электромагнитного импульсного (ЭМИ) СШП зондирования подстилающей среды [6], в котором особое место занимает антенная тематика, поскольку вопрос о согласовании импедансов антенны и среды остаётся открытым.
Последнее обусловлено общими закономерностями поведения грунтов в переменном электромагнитном поле - почва любой подстилающей среды является многофазной гетерогенной дисперсной системой, состояние которой, как правило, неизвестно. Для неё характерны процессы поляризации, релаксации и электропроводности, которые во многом определяются наличием в почве поверхностей раздела фаз, обусловливающих величину поверхностной проводимости, а значит, и поверхностного импеданса. На этих поверхностях происходит формирование объёмных зарядов и двойных электрических слоёв (Г. Л. Ф. Гельмгольц, 1879), в свою очередь определяющих значения как напряжённости внутреннего электрического поля среды, так и контактной разности потенциалов. Нижнюю границу частотного диапазона отражённого сигнала определяет ионный обмен в почве (её способности к поглощению и обмену ионами на границе двух фаз). В почве превалирует катионный обмен.
Фактически, говоря о поглотительной способности (ёмкости катионного обмена) почвы по отношению к внешнему электромагнитному полю, имеется в виду, что её обменная способность сосредоточена, в основном, в её тонких, в первую очередь коллоидной, фракциях, а сами почвенные коллоиды подразделяются на электроотрицательные гели и изоэлектрические осадки. Как правило, катионы с более высоким зарядом обладают большей энергией поглощения, а при равных зарядах - с большей атомной массой (К. К. Гедройц, 1955; Н. И. Горбунов, 1948; Ф. Дюшофур, 1970; Д. С. Орлов, 1985).
Существует большое количество методов определения ёмкости катионного обмена почв. Вместе с тем, до сих пор, как отметил Б.П.Никольский (1934), вопрос об определении абсолютной ёмкости поглощения [7] почв не может быть решен ни практически, ни даже теоретически, т.е. в нашем случае - величина поверхностной проводимости, а следовательно, и поверхностного импеданса, является величиной умозрительной. Тем острее встаёт вопрос об исследованиях в области СШП антенн для подповерхностного зондирования.
До сегодняшнего дня не решён ряд задач по созданию приёмных антенн, минимально искажающих структуру наблюдаемого поля и контролю излучения в подстилающей среде.
К антеннам предъявляются жесткие, порой трудно совместимые требования: стабильность электродинамических характеристик в широком частотном диапазоне, электромагнитная совместимость, малые вес и габариты, технологичность изготовления и т.д. В дополнение к перечисленному, при моделировании антенн, предназначенных для излучения и приёма ЭМИ СШП сигналов, изначально закладывается, что они должны иметь чётко выраженный фазовый центр, постоянную амплитудно -частотную и линейную фазо-частотную характеристики в полосе частот, содержащей доминирующую часть спектра сигнала [8].
Процесс
излучения СШП сигнала имеет значительные отличия от процесса излучения узкополосного
сигнала и поэтому использование некоторых методов из теории антенн становится
затруднительным [3]. Аналитическое решение внутренней задачи для
антенн подповерхностного зондирования при возбуждении их токами ![]() вызывает значительные математические
трудности, связанные с тем, что при таких токах антенны автоматически начинают
проявлять в своём составе достаточно чётко выделяемые излучатели электрического
и магнитного типов [4]. Успех разработки
удачной конструкции антенны обычно связывают с наличием в ней конструктивных
элементов, обеспечивающих возможность эффективного обмена энергией между этими излучателями [5]. Что касается теоретических
исследований, то они пока отстают от имеющихся экспериментальных наработок.
вызывает значительные математические
трудности, связанные с тем, что при таких токах антенны автоматически начинают
проявлять в своём составе достаточно чётко выделяемые излучатели электрического
и магнитного типов [4]. Успех разработки
удачной конструкции антенны обычно связывают с наличием в ней конструктивных
элементов, обеспечивающих возможность эффективного обмена энергией между этими излучателями [5]. Что касается теоретических
исследований, то они пока отстают от имеющихся экспериментальных наработок.
Возникает вопрос о применении численных методов, как это обычно делается при рассмотрении ряда сложных задач электродинамики. Подобный подход в данных конкретных задачах применяется, например, в [6-7], ряд вычислительных трудностей связан также с решением интегральных уравнений [8, 9].[9] На практике форма тока в антенне обычно задаётся исходя из удобства проведения расчётов [10]. Такая условность наиболее ощутима при наличии кривизны в антеннах, например, спиральных [11] [10].
Значительно возрос интерес к исследованиям, направленным на более тщательное изучение факторов, определяющих полосу пропускания антенн, поскольку частотная зависимость входного импеданса антенны, обусловленная влиянием подстилающей среды, затрудняет качественное согласование антенны в широкой полосе частот.
Расширение рабочей полосы частот по качеству согласования входного импеданса возможно двумя способами:
- применением так называемых широкополосно – согласующих цепей на входе антенны при неизменной конструкции излучающей системы;
- оптимизацией формы (конструкции) излучающей системы с целью получения входного импеданса, мало меняющегося по частоте. Здесь можно назвать применение утолщённых вибраторов и щелей увеличенной ширины; различные приёмы взаимной компенсации нескольких отражений внутри излучающей системы путём рационального выбора точек питания и соответствующих шунтов [12].
Как правило, при анализе ЭМИ СШП излучения рассматривают возбуждение апертурной антенны [13, 14], реже - антенны с бегущей волной [15]. Однако перспективность применения антенны с бегущей волной (АБВ) как набора связанных отрезков плавных неоднородных линий передачи (НЛП) обусловлена тем, что частотные свойства таких отрезков зависят не только от длины линии, как у отрезков однородных линий передачи, но и от закона изменения волнового сопротивления. Кроме этого, в плавных НЛП легко реализуется один из эффективных способов трансформации волнового сопротивления за счёт изменения погонных параметров линии.
Термин «нерегулярная (неоднородная) линия передачи» является в известном смысле обобщающим и включает в себя объекты различной физической природы, внешние параметры которых могут быть описаны дифференциальными уравнениями (ДУ), имеющими в нашем случае вид телеграфных уравнений длинной линии [16, 17]. Расчету классических и волновых матриц n-проводных связанных линий посвящены работы [18-22]. Отличительная особенность таких уравнений применительно к НЛП проявляется в зависимости коэффициентов ДУ от пространственных неоднородностей. Вследствие этого элементы классических и волновых матриц отрезка НЛП, рассматриваемого в качестве некоторого эквивалентного четырехполюсника, также будут функциями координат.
Разработка теории плавных неоднородных линий и их проектирование основывается на теории цепей [23] и является важным самостоятельным разделом современной прикладной электродинамики. Наиболее полные данные по строгому подходу к анализу основных типов НЛП содержатся в [24].
В последнее время получили развитие методы, позволяющие рассчитать характеристики излучения СШП антенн, основанные на решении уравнения Поклингтона относительно неизвестного распределения тока в тонком электрическом вибраторе [8, 9, 25-27] [11].
В общем случае в связанных токоведущих линиях распространяются волны, имеющие сложную структуру с продольными Е- и Н- составляющими [28]. Классификация волн, исходя из анализа условий их существования, представляет собой относительно мало изученную проблему даже в отношении простых конструкций одиночных токоведущих линий, не говоря уже о связанных структурах [24, 29]. Поэтому при моделировании токоведущих линий чаще всего исходят из концепции существования так называемых «квази Т- волн» [29] [12].
Существует несколько причин введения квази Т- приближения:
- в настоящее время нет альтернативных решений, предоставляющих разработчикам ВЧ узлов более эффективный матричный аппарат анализа;
- концепция нормальных волн как естественное расширение понятия «квази Т - волна» применима для анализа структур с почти поперечными волнами, а также для структур с более сложной конфигурацией электромагнитного поля посредством увеличения связности эквивалентной схемы [16, 17, 30].
Ввиду сложности
нахождения точных решений основных уравнений НЛП для произвольной функции
волнового сопротивления ![]() широкое распространение
получили приближённые методы или методы параметрической оптимизации, которые
можно разбить на две группы:
широкое распространение
получили приближённые методы или методы параметрической оптимизации, которые
можно разбить на две группы:
- первая объединяет стандартные методы теории ДУ (метод неопределенных коэффициентов, представление в виде степенных рядов, разложение по малому параметру, сведение ДУ к интегральным уравнениям с их последующим решением);
- вторая группа в своей основе содержит физические предпосылки, упрощающие исходные уравнения настолько, что могут быть найдены их замкнутые решения. Далее для простоты и наглядности представлены результаты второй группы.
Индуктивность как объект параметрической оптимизации
Классическим примером НЛП
является длинная линия с непрерывно изменяющимися погонными параметрами –
плавная неоднородная линия передачи, для
которой коэффициент отражения ![]() как элемент матрицы
рассеяния
как элемент матрицы
рассеяния ![]() описывается уравнением Риккати (А. Л.
Фельдштейн и Ф. Болиндер, 1950):
описывается уравнением Риккати (А. Л.
Фельдштейн и Ф. Болиндер, 1950):
![]() (1)
(1)
где ![]() -
постоянная распространения волны;
-
постоянная распространения волны; ![]() - характеристическая
функция НЛП (функция местных отражений).
- характеристическая
функция НЛП (функция местных отражений).
Приближённое решение (1)
идентично элементу ![]() матрицы рассеяния
матрицы рассеяния ![]() [24]. Как правило, решение (1) ищется для
граничных условий
[24]. Как правило, решение (1) ищется для
граничных условий ![]() Ом и
Ом и ![]() Ом.
Ом.
Из (1) следует, что волновое сопротивление и коэффициент замедления являются сложными функциями пространственной координаты. Это означает, что в процедуре параметрической оптимизации антенны подповерхностного зондирования компонентами вектора варьируемых параметров являются размеры поперечных (параллельных дневной поверхности) сечений токоведущих линий антенны.
В
нашем случае для излучения ЭМИ СШП сигналов в подповерхностную среду из четырёх
антенн, представленных в [31], используется микрополосковая антенна (МПА),
поэтому особый интерес представляют две постоянные времени, характерные для эквивалентной
схемы несимметричной связанной полосковой линии - ![]() ,
, ![]() [13].
Первая постоянная времени обусловливает трансформацию тока в телеграфных
уравнениях, вторая – трансформацию напряжения.
[13].
Первая постоянная времени обусловливает трансформацию тока в телеграфных
уравнениях, вторая – трансформацию напряжения.
Поскольку ударное возбуждение антенны производится ДДРВ генератором, излучение антенны подповерхностного зондирования происходит в режиме больших импульсных токов, когда антенна проявляет себя как магнитный диполь [4], наиболее полной электродинамической характеристикой которого является погонная индуктивность. Покажем это.
Пусть
отрезок НЛП длиной ![]() включен между двумя
полубесконечными регулярными линиями передачи с различными волновыми
(характеристическими) сопротивлениями
включен между двумя
полубесконечными регулярными линиями передачи с различными волновыми
(характеристическими) сопротивлениями ![]() и
и ![]() (рис. 1). Выделим элементарный участок
длиной
(рис. 1). Выделим элементарный участок
длиной ![]() , малый настолько, что в его пределах
погонные сопротивление
, малый настолько, что в его пределах
погонные сопротивление ![]() , проводимость
, проводимость ![]() , индуктивность
, индуктивность ![]() и
ёмкость
и
ёмкость ![]() можно полагать не зависящими от
координаты
можно полагать не зависящими от
координаты ![]() . Допуская в пределах этого отрезка поперечный
характер электромагнитного поля (основное допущение теории НЛП для Т-волн
[32]), можно записать систему ДУ для напряжения
. Допуская в пределах этого отрезка поперечный
характер электромагнитного поля (основное допущение теории НЛП для Т-волн
[32]), можно записать систему ДУ для напряжения ![]() и тока
и тока
![]() в виде
в виде
где ![]() и
и ![]() –
комплексные сопротивление и проводимость на единицу длины. Связь (1) и (2)
устанавливает величина
–
комплексные сопротивление и проводимость на единицу длины. Связь (1) и (2)
устанавливает величина  - характеристическое
(волновое) сопротивление, тогда в (1)
- характеристическое
(волновое) сопротивление, тогда в (1) ![]() . Для
совместного решения (1) и (2) вводят понятие «входной импеданс» как
. Для
совместного решения (1) и (2) вводят понятие «входной импеданс» как
![]()
имеющий Фурье образ вида ![]() [14];
где
[14];
где ![]() - измеряемые величины. Аналогичные Фурье-образы
можно получить прямым измерением как коэффициента отражения
- измеряемые величины. Аналогичные Фурье-образы
можно получить прямым измерением как коэффициента отражения ![]() из (1), так и составляющих
из (1), так и составляющих ![]() и
и ![]() из (2)
-
из (2)
- ![]() и
и ![]() , при
этом
, при
этом ![]() - Фурье образ
- Фурье образ ![]() ,
, ![]() - Фурье образ
- Фурье образ ![]() . Таким
образом, для всех входящих в уравнения (1) и (2) величин существуют измеряемые
Фурье образы.
. Таким
образом, для всех входящих в уравнения (1) и (2) величин существуют измеряемые
Фурье образы.
Компоненты
вектора варьируемых параметров в виде элементов ![]() можно представить как
импеданс четырехполюсника в виде:
можно представить как
импеданс четырехполюсника в виде:
 , (3)
, (3)
![]() -
-
фаза между током и напряжением.
Импеданс подстилающей среды запишем как
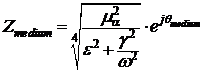 , (4)
, (4)
где  -
фазовая характеристика среды.
-
фазовая характеристика среды.
Здесь
аргумент функции ![]() в (4) - известные граничные условия Леонтовича – Щукина [33]: отношение
плотности токов проводимости
в (4) - известные граничные условия Леонтовича – Щукина [33]: отношение
плотности токов проводимости ![]() к плотности токов
смещения
к плотности токов
смещения ![]() ,
,
![]() .
(5)
.
(5)
Рассмотрим синфазность волнового сопротивления антенны и импеданса среды
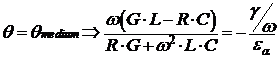 . (6)
. (6)
или
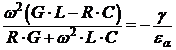 . (7)
. (7)
Очевидно, что
![]() . (8)
. (8)
и
![]() . (9)
. (9)
Следовательно, для
согласования волновых сопротивлений антенны и среды по фазовым распределениям
необходимо соблюдение соотношения (9), где ![]() ;
; ![]() [Ф/м];
[Ф/м]; ![]() - чисто
электродинамические характеристики[15].
Для большинства сред правая часть (9) в низкочастотном пределе составляет
величину порядка 7 МГц.
- чисто
электродинамические характеристики[15].
Для большинства сред правая часть (9) в низкочастотном пределе составляет
величину порядка 7 МГц.
Моделирование параметров погонной индуктивности с учётом влияния земли
Наиболее характерным
примером НЛП (рис. 1) является неоднородная несимметричная полосковая линия
передачи [10]. Для неё рассмотрим поведение ![]() с
учётом влияния поверхности [34]. Расчет
с
учётом влияния поверхности [34]. Расчет ![]() производится
методом конформных отображений с учетом рис. 2. При малых t [24]
производится
методом конформных отображений с учетом рис. 2. При малых t [24]
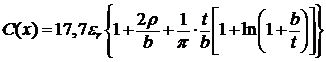 .
.
что можно записать как
![]() , где
, где ![]() .
.
Для схемы НЛП (рис. 2) с электропроводностью
токоведущего проводника ![]()
![]() ,
,
т. е. ![]() , где
, где ![]() . Тогда закон изменения
. Тогда закон изменения ![]() примет вид
примет вид
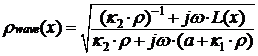 .
.
![]() берем
из схемы, представленной на рис. 3. Из обхода контура «крыло АБВ – подстилающая
поверхность – крыло АБВ» (рис. 3б) следует, что приложенное напряжение
расходуется на преодоление э.д.с. самоиндукции
берем
из схемы, представленной на рис. 3. Из обхода контура «крыло АБВ – подстилающая
поверхность – крыло АБВ» (рис. 3б) следует, что приложенное напряжение
расходуется на преодоление э.д.с. самоиндукции ![]() и
э.д.с. взаимоиндукции
и
э.д.с. взаимоиндукции ![]() (
(![]() - ток в
первом «крыле»,
- ток в
первом «крыле», ![]() - ток во втором). Собственная
индуктивность АБВ состоит из индуктивностей «крыльев»
- ток во втором). Собственная
индуктивность АБВ состоит из индуктивностей «крыльев» ![]() ,
их взаимной индуктивности
,
их взаимной индуктивности ![]() и может быть
представлена как
и может быть
представлена как
![]() . (10)
. (10)
По определению
где ![]() - среднее геометрическое расстояние площади
поперечного сечения токопровода, определение дано в [34];
- среднее геометрическое расстояние площади
поперечного сечения токопровода, определение дано в [34]; ![]() - расстояние между произвольными
элементами площади крыльев антенны
- расстояние между произвольными
элементами площади крыльев антенны ![]() и
и![]() .
.
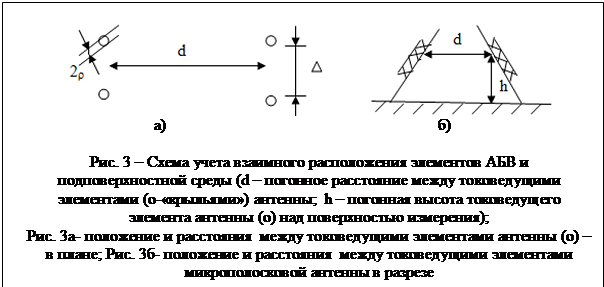
На рис. 4. приведена фигура для нахождения
![]() для схемы учета взаимного расположения
элементов антенны (рис. 3а) и подповерхностной среды (рис. 3б).
для схемы учета взаимного расположения
элементов антенны (рис. 3а) и подповерхностной среды (рис. 3б).
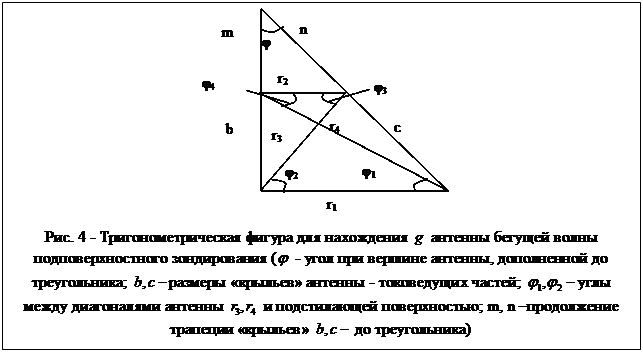
Формула для определения
![]() антенны [34] с учётом обозначений,
приведенных на рис. 4, имеет вид
антенны [34] с учётом обозначений,
приведенных на рис. 4, имеет вид
Поскольку в (12) не участвуют
размеры поперечных
сечений токоведущих линий, величина ![]() может считаться постоянной
(величину
может считаться постоянной
(величину ![]() определяем из рис. 4,
определяем из рис. 4, ![]() ):
):
С учётом влияния
подстилающей поверхности ![]() из (10) можно записать
как [34]
из (10) можно записать
как [34]
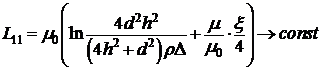 . (13)
. (13)
«Крылья» антенны
симметричны, поскольку они через угол раскрыва антенны задают направление
излучения, т. е. ![]() , а значение под логарифмом –
масштабный коэффициент антенны. Предположим
, а значение под логарифмом –
масштабный коэффициент антенны. Предположим
 , (14)
, (14)
тогда 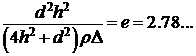 , или
, или ![]() .
.
Из этого следует, что текущая
толщина токопроводов ![]() и расстояние между ними
и расстояние между ними ![]() (ширина щели) являются функцией вида
антенны
(ширина щели) являются функцией вида
антенны![]() , где
, где ![]() -
высота над уровнем подстилающей поверхности. Требование
-
высота над уровнем подстилающей поверхности. Требование ![]() означает,
с одной стороны, для
означает,
с одной стороны, для ![]() из (13) переход к погонным
параметрам с учётом влияния поверхности (земли), с другой стороны – задание
целевой функции для размеров поперечных сечений токоведущих линий
антенны.
из (13) переход к погонным
параметрам с учётом влияния поверхности (земли), с другой стороны – задание
целевой функции для размеров поперечных сечений токоведущих линий
антенны.
Размеры поперечных сечений токоведущей линии и щели вида
представляют собой уравнение АБВ подповерхностного зондирования [35]. Из (15) можно получить целевую функцию в виде
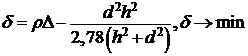 .
.
Изменение условия (14) приводит лишь к изменению коэффициента в знаменателе, т.е. значение логарифма - масштабный коэффициент антенны.
В (13) ![]() - коэффициент, учитывающий поверхностный
эффект - зависимость изменения составляющей погонной индуктивности от частоты
- коэффициент, учитывающий поверхностный
эффект - зависимость изменения составляющей погонной индуктивности от частоты ![]() , проводимости материала антенны
, проводимости материала антенны ![]() и ширины токопровода
и ширины токопровода ![]() [34]:
[34]:
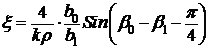 ,
,
где ![]() – аргумент и модуль функции Бесселя
– аргумент и модуль функции Бесселя ![]() – 1-го рода нулевого порядка;
– 1-го рода нулевого порядка; ![]() – аргумент и модуль функции Бесселя
– аргумент и модуль функции Бесселя ![]() – 1-го рода первого порядка; где
– 1-го рода первого порядка; где ![]() ;
; ![]() Гн/м. Здесь
в
Гн/м. Здесь
в ![]() ,
, ![]() в
качестве аргумента используется
в
качестве аргумента используется ![]() . Результаты моделирования
коэффициента
. Результаты моделирования
коэффициента ![]() приведены на рис. 5. Например, для ширины
полосы (
приведены на рис. 5. Например, для ширины
полосы (![]() ) частот в две октавы (10 МГц÷1
ГГц), положив
) частот в две октавы (10 МГц÷1
ГГц), положив ![]() м,
м, ![]() См/м -
проводимость меди, находим:
См/м -
проводимость меди, находим:
![]()
![]()
![]() .
.
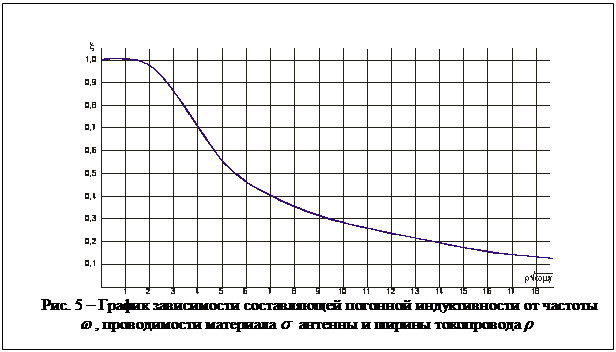
Из результатов моделирования коэффициента
![]() следует, что физические параметры
антенны, при которых
следует, что физические параметры
антенны, при которых ![]() , существуют.
, существуют.
Для реальной антенны (рис. 6) по
формуле (11) для нахождения ![]() было проведено
математическое моделирование, в результате которого выявлено, что величину
взаимной индуктивности
было проведено
математическое моделирование, в результате которого выявлено, что величину
взаимной индуктивности ![]() может считать постоянной (
может считать постоянной (![]() ,где
,где ![]() взаимная индуктивность центральных
проводников площадью
взаимная индуктивность центральных
проводников площадью ![]() и
и ![]() ,
, ![]() взаимная индуктивность второго проводника
– первого слева или справа от центрального проводника). Оценка погрешности моделирования
по (11) относительно расчёта по (12) лежит в пределах
взаимная индуктивность второго проводника
– первого слева или справа от центрального проводника). Оценка погрешности моделирования
по (11) относительно расчёта по (12) лежит в пределах ![]() при
погрешности самого метода среднего геометрического расстояния
при
погрешности самого метода среднего геометрического расстояния ![]() [36]. Таким образом, при соблюдении
условия (15) погонная индуктивность может не зависеть от высоты до поверхности
измерения и от расстояния между токоведущими элементами («крыльями») антенны. Ранее
считалось, что должно быть
[36]. Таким образом, при соблюдении
условия (15) погонная индуктивность может не зависеть от высоты до поверхности
измерения и от расстояния между токоведущими элементами («крыльями») антенны. Ранее
считалось, что должно быть ![]() .
.
Результаты экспериментальных измерений частотных характеристик неоднородной микрополосковой антенны подповерхностного зондирования
Разработанная в
соответствии с (15) АБВ состоит из связанных неоднородных несимметричных
микрополосковых линий (рис. 6, 6а)
[16],
т.е. представляет собой неоднородную микрополосковую антенну (МПА) [35]. Для
проверки работоспособности зависимости (15) для антенны [35] проведены
измерения её частотных характеристик как АБВ подповерхностного зондирования (измерения
проводились на сухом бетоне). Частотные характеристики антенн в полосе от 300
кГц до 1.5 ГГц получены с помощью измерителя параметров четырехполюсника
OBZOR-103. Вид лабораторной установки на базе OBZOR-103 и её характеристики
даны в [31]. Сравнивались две антенны: для первой ![]() , для
второй -
, для
второй -![]() («меандровая» полоска).
(«меандровая» полоска).
Внешний
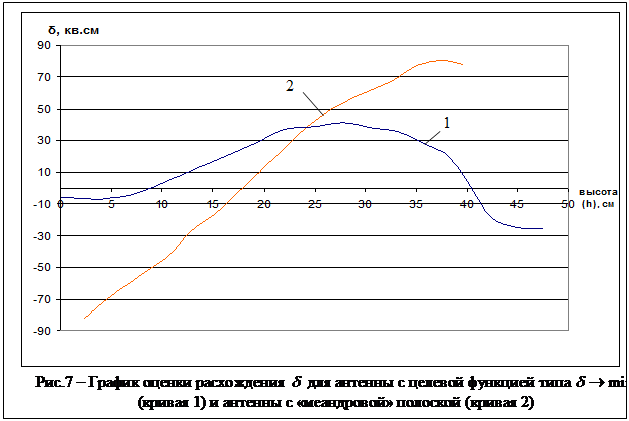
вид микрополосковой антенны приведен на рис. 6, 6а. Оценки расхождения ![]() для антенн двух типов приведены на рис. 7.
Очевидно, что минимаксная величина
для антенн двух типов приведены на рис. 7.
Очевидно, что минимаксная величина ![]() для антенны,
представленной на рис. 6, меньше
для антенны,
представленной на рис. 6, меньше ![]() для
антенны с «меандровой» полоской (
для
антенны с «меандровой» полоской (![]() ) в
) в ![]() раза.
раза.
Известно, что для получения
низкого коэффициента стоячей волны по напряжению (![]() ) в
длинноволновой части диапазона приёмных СШП антенн распределённая нагрузка
должна быть протяжённой (например, РК - кабель), поэтому для согласования
собственно приёмной СШП антенны и РК–кабеля с приёмным устройством рациональнее
использовать сосредоточенный резистор. Для обеспечения согласования в широкой
полосе частот [37, 38] желательно резистор установить в торце регулярной
короткозамкнутой коаксиальной линии. Для резисторов паразитную ёмкость можно
ориентировочно определить по формуле
) в
длинноволновой части диапазона приёмных СШП антенн распределённая нагрузка
должна быть протяжённой (например, РК - кабель), поэтому для согласования
собственно приёмной СШП антенны и РК–кабеля с приёмным устройством рациональнее
использовать сосредоточенный резистор. Для обеспечения согласования в широкой
полосе частот [37, 38] желательно резистор установить в торце регулярной
короткозамкнутой коаксиальной линии. Для резисторов паразитную ёмкость можно
ориентировочно определить по формуле
![]() ,
,
где ![]() геометрические
параметры резистора. Для резисторов типа С6-4, С6-9 ёмкость составляет 0.085
пФ. Компенсация емкостей может быть выполнена введением компенсирующей
индуктивности. Погонная индуктивность находится по формуле
геометрические
параметры резистора. Для резисторов типа С6-4, С6-9 ёмкость составляет 0.085
пФ. Компенсация емкостей может быть выполнена введением компенсирующей
индуктивности. Погонная индуктивность находится по формуле
![]() ,
,
![]() диаметры
внешнего и внутреннего торца регулярной короткозамкнутой коаксиальной линии.
диаметры
внешнего и внутреннего торца регулярной короткозамкнутой коаксиальной линии.
Для такого антенно –
фидерного устройства (собственно антенна; РК- кабель; СВЧ – тройник с
согласующим резистором) выполнены измерения погонных параметров в частотной
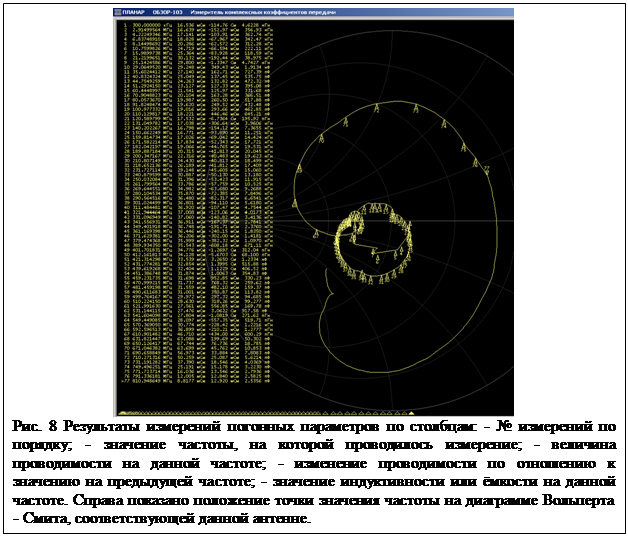
области. Результаты измерений приведены на рис. 8. Обращают на себя внимание
значения индуктивности на частоте 120.58 МГц – 195.92 пГн (![]() Гн), в районе 400 МГц -
Гн), в районе 400 МГц - ![]() Гн, и т.д. Подобные величины позволяют
говорить о том, что такой способ задания индуктивности позволяет реализовывать
величины в десятки пикагенри и единицы пикофарад.
Гн, и т.д. Подобные величины позволяют
говорить о том, что такой способ задания индуктивности позволяет реализовывать
величины в десятки пикагенри и единицы пикофарад.
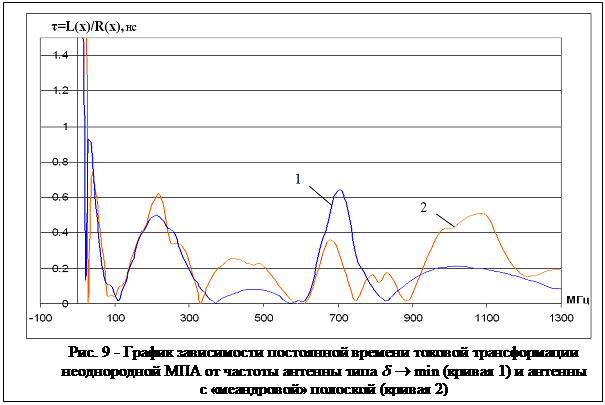
По результатам измерений
компонент Фурье образа вектора варьируемых параметров ![]() ,
входящих в (2), построен график зависимости постоянной времени токовой
трансформации
,
входящих в (2), построен график зависимости постоянной времени токовой
трансформации ![]() антенны от частоты (рис. 9).
Очевидно, что
антенны от частоты (рис. 9).
Очевидно, что ![]() первой антенны меньше
первой антенны меньше ![]() второй в диапазоне частот 0.3-700 МГц.
второй в диапазоне частот 0.3-700 МГц.
Все данные, представленные на рис.7÷14, получены экспериментально.
Анализ полученных экспериментальных данных[17]
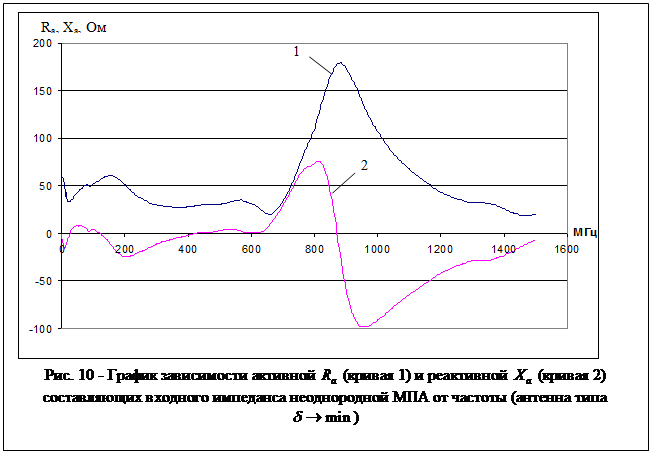
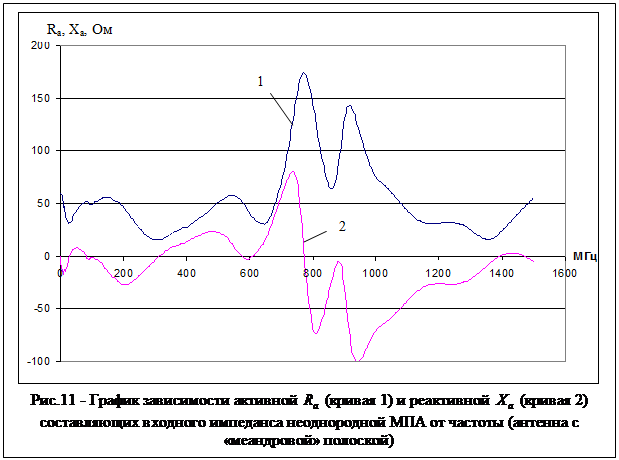
Из приведенных на рис. 10,
11 графиков зависимости активной ![]() (кривая 1) и реактивной
(кривая 1) и реактивной
![]() (кривая 2) составляющих входного
импеданса очевидно, что
(кривая 2) составляющих входного
импеданса очевидно, что ![]() первой антенны меньше
первой антенны меньше
![]() второй (рис. 10, 11 – кривая 1), т.е.
первая антенна частотно менее зависима, чем вторая; у первой антенны резонанс
токов по частоте выше (
второй (рис. 10, 11 – кривая 1), т.е.
первая антенна частотно менее зависима, чем вторая; у первой антенны резонанс
токов по частоте выше (![]() при 882 МГц), чем у
второй -
при 882 МГц), чем у
второй - ![]() при 770.7 и 917 МГц. Реактивная
составляющая
при 770.7 и 917 МГц. Реактивная
составляющая ![]() первой антенны (рис. 10 – кривая 2) в диапазоне
частот 20
первой антенны (рис. 10 – кривая 2) в диапазоне
частот 20![]() 100 МГц носит индуктивный характер (
100 МГц носит индуктивный характер (![]()
![]() Ом), в диапазоне частот 100
Ом), в диапазоне частот 100![]() 400
МГц – емкостной (
400
МГц – емкостной (![]() max
max![]() Ом), в диапазоне частот 400
Ом), в диапазоне частот 400![]() 600 МГц - индуктивный (
600 МГц - индуктивный (![]()
![]() Ом). У второй антенны
во всём диапазоне частот
Ом). У второй антенны
во всём диапазоне частот ![]() носит переменный
индуктивно – емкостной характер
носит переменный
индуктивно – емкостной характер ![]() Ом (рис. 11 - кривая
2). В диапазоне частот 0-700 МГц у первой антенны
Ом (рис. 11 - кривая
2). В диапазоне частот 0-700 МГц у первой антенны
![]() Ом,
у второй -
Ом,
у второй - ![]() Ом.
Ом.
Спектр собственных частот
обеих антенн: число точек резонансов напряжений ![]() - 3 у
первой (24.66; 122.15; 429.6 МГц) и 6 у второй (28.42; 86.4; 313.3; 575.6;
609.5; 774.5 МГц); резонансов токов
- 3 у
первой (24.66; 122.15; 429.6 МГц) и 6 у второй (28.42; 86.4; 313.3; 575.6;
609.5; 774.5 МГц); резонансов токов ![]() - у первой антенны – 1
(882 МГц), у второй – 2 (770.6; 917 МГц). Это свидетельствует о том, что
влияние
- у первой антенны – 1
(882 МГц), у второй – 2 (770.6; 917 МГц). Это свидетельствует о том, что
влияние ![]() первой антенны много меньше влияния
первой антенны много меньше влияния ![]() второй антенны (15). Поведение кривых 1,
2 на рис. 10 соответствует поведению кривых расчёта входного сопротивления
вибратора по интегральному уравнению Халлена [8].
второй антенны (15). Поведение кривых 1,
2 на рис. 10 соответствует поведению кривых расчёта входного сопротивления
вибратора по интегральному уравнению Халлена [8].
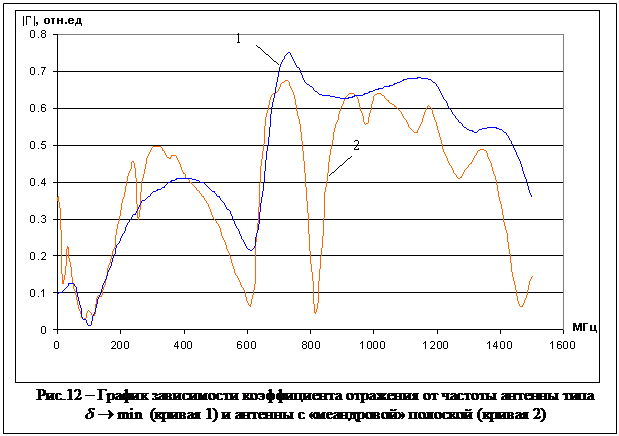
Из сравнения кривых 1, 2 графика
зависимости ![]() от частоты (рис. 12) следует, что у антенны
типа
от частоты (рис. 12) следует, что у антенны
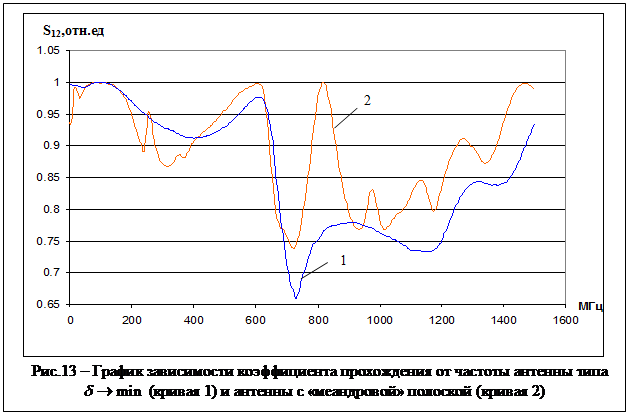
типа ![]() эта зависимость более гладкая. На рис. 13
представлены коэффициенты прохождения первой и второй антенн, пересчитанные как
элемент
эта зависимость более гладкая. На рис. 13
представлены коэффициенты прохождения первой и второй антенн, пересчитанные как
элемент ![]() матрицы рассеяния
матрицы рассеяния ![]() реактивного
четырехполюсника [18],
реактивного
четырехполюсника [18],
![]() .
.
Преимущества первой
антенны над второй: более гладкая кривая ![]() ; на рис.13
показано, что неравномерность кривой
; на рис.13
показано, что неравномерность кривой ![]() в диапазоне частот 0.3
в диапазоне частот 0.3![]() 700 МГц у первой антенны – 8.5%; у второй
– 13.5%.
700 МГц у первой антенны – 8.5%; у второй
– 13.5%.
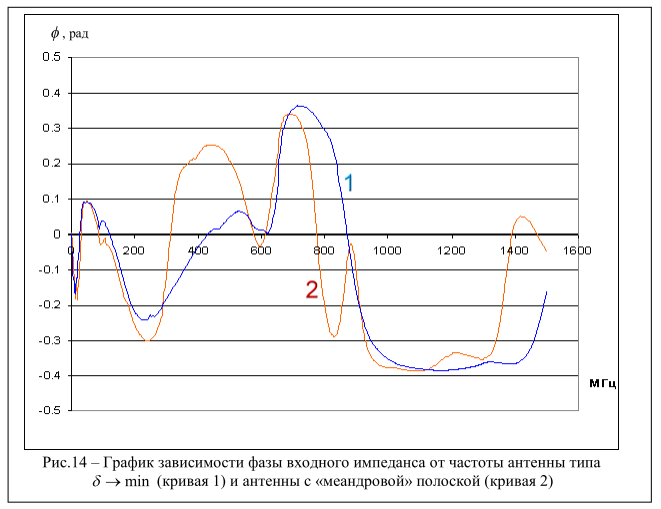
На рис. 14 представлены фазы входных импедансов первой и второй антенн. Здесь фаза входного импеданса определена как
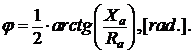
Фазы входных импедансов первой и
второй антенн определяют запаздывание токов смещения относительно токов
проводимости в антенне. Из графиков, представленных на рис. 14 видно, что у
первой антенны (![]() ) фазовый набег меньше: в диапазоне
частот 0.3
) фазовый набег меньше: в диапазоне
частот 0.3![]() 700 МГц изменяется от -13.8º до
+20.8º, у второй - от -17º до +19.3º(
700 МГц изменяется от -13.8º до
+20.8º, у второй - от -17º до +19.3º(![]() ).
).
Экспериментальная проверка чувствительности антенны к изменению импеданса подстилающей среды
Хорошо известно [39] существование
ярко выраженных минимумов ![]() для границы
«воздух-грунт». Так, при различных температурах и соленостях (проводимости)
модуль коэффициента отражения параллельной поляризации
для границы
«воздух-грунт». Так, при различных температурах и соленостях (проводимости)
модуль коэффициента отражения параллельной поляризации ![]() монотонно
уменьшается с увеличением угла падения волны
монотонно
уменьшается с увеличением угла падения волны ![]() , с
ростом частоты и понижением температуры (
, с
ростом частоты и понижением температуры (![]() ) – т.е.
с уменьшением влияния токов проводимости. С понижением
) – т.е.
с уменьшением влияния токов проводимости. С понижением ![]() грунта
глубина минимума
грунта
глубина минимума ![]() на низких частотах уменьшается,
а на высоких возрастает. При этом зависимость угла падения становится более
заметной на высоких частотах.
на низких частотах уменьшается,
а на высоких возрастает. При этом зависимость угла падения становится более
заметной на высоких частотах.
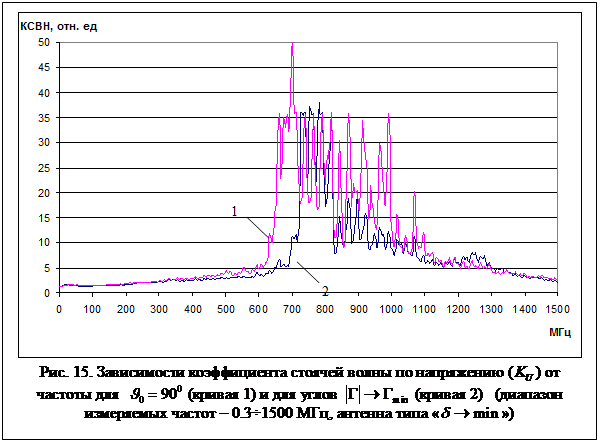
С целью подтверждения этой
зависимости для разных углов раскрыва антенны (рис. 6) были измерены значения ![]() как функции частоты со значениями
как функции частоты со значениями ![]() , близкими к минимальным значениям (
, близкими к минимальным значениям (![]() ) и для угла падения волны
) и для угла падения волны ![]() 0=90º (графики зависимости
0=90º (графики зависимости ![]() - рис. 15, 15а).
- рис. 15, 15а).
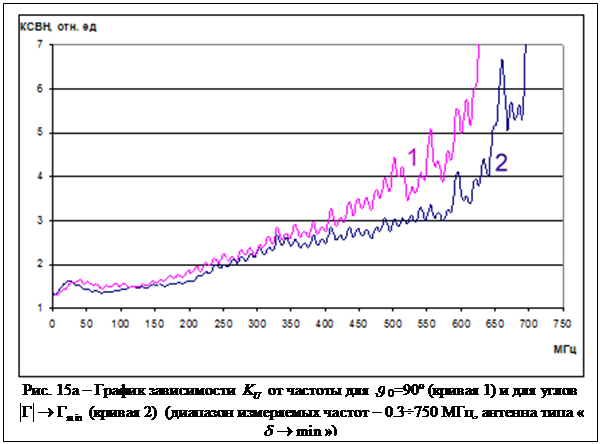
Из значений ![]() , приведенных на рис. 15, 15а, видно, что
использование угла раскрыва антенны, обеспечивающего угол падения волны 68о
<
, приведенных на рис. 15, 15а, видно, что
использование угла раскрыва антенны, обеспечивающего угол падения волны 68о
<![]() 0< 72о, расширяет
полосу антенны @ на
10% по сравнению с углом раскрыва антенны, обеспечивающего угол падения волны
0< 72о, расширяет
полосу антенны @ на
10% по сравнению с углом раскрыва антенны, обеспечивающего угол падения волны ![]() 0=90º, что подтверждает наличие
ярко выраженных минимумов модуля коэффициента отражения для границы
«воздух-грунт».
0=90º, что подтверждает наличие
ярко выраженных минимумов модуля коэффициента отражения для границы
«воздух-грунт».
Для проверки чувствительности антенны
к изменению поверхностного импеданса подстилающей среды проведены измерения ![]() антенн, расположенных на различных
подстилающих поверхностях (сухой бетон, снег). Результаты измерений приведены
на рис. 16, 16 а.
антенн, расположенных на различных
подстилающих поверхностях (сухой бетон, снег). Результаты измерений приведены
на рис. 16, 16 а.
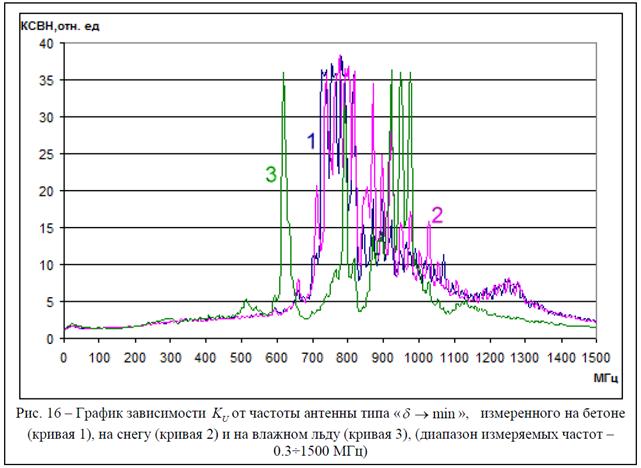
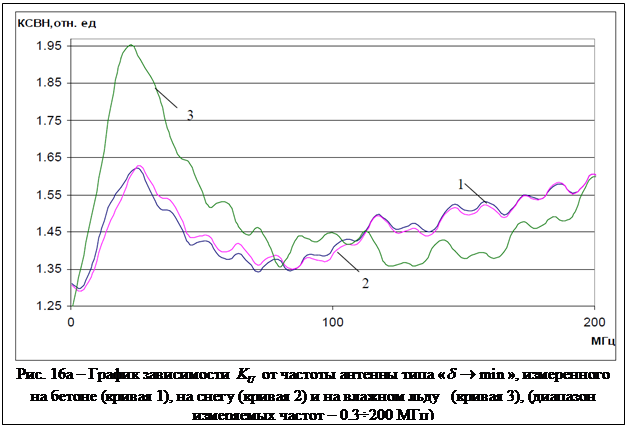
Из результатов измерений следует, что изменение импедансных свойств подстилающей поверхности влияет на характеристики антенны двояко (кривые 1, 2 на рис. 16,а). Расхождение результатов на рис. 16, начиная с 800 МГц, говорит о наличии реакции антенны на расхождение импедансов бетона и снега. Подобие результатов, представленных на рис. 16,а (кривые 1, 2), позволяет судить о близких по величине значениях импедансов.
Это может быть
обусловлено тем, что в этих структурах вода отсутствует полностью, а значит,
она не участвует в формировании импедансных свойств подстилающей поверхности -
в сухом бетоне скелет представляет собой чешуйчатую структуру и влажность не
превышает сотых долей процента, в снеге (![]() ) вода
выморожена полностью и снег представляет чисто кристаллическую структуру.
Кривая 3 на рис. 16, 16а соответствует измерениям, когда в качестве импедансной
поверхности выступает влажный лёд. Различия между кривыми 1, 2 и 3,
соответствующими сухому бетону, снегу и влажному льду, очевидны. Следует
отметить, что для влажного льда резко возрастает коэффициент отражения в
диапазоне частот 17-28 МГц, что может рассматриваться как признак частотной
дисперсии поверхностного импеданса, обусловленной наличием водной плёнки на
поверхности льда[18]
[19].
) вода
выморожена полностью и снег представляет чисто кристаллическую структуру.
Кривая 3 на рис. 16, 16а соответствует измерениям, когда в качестве импедансной
поверхности выступает влажный лёд. Различия между кривыми 1, 2 и 3,
соответствующими сухому бетону, снегу и влажному льду, очевидны. Следует
отметить, что для влажного льда резко возрастает коэффициент отражения в
диапазоне частот 17-28 МГц, что может рассматриваться как признак частотной
дисперсии поверхностного импеданса, обусловленной наличием водной плёнки на
поверхности льда[18]
[19].
Природа волн, излучаемых неоднородной микрополосковой антенной
Неоднородная МПА заканчивается линией, разомкнутой на конце. Порядок расчёта краевой ёмкости этой линии дан в [29].
При построении излучающей системы МПА можно учесть поверхностные электрические токи, текущие по металлической (медной) пластине и по экрану, а также вертикальные токи электрической поляризации в диэлектрической подложке - область растекания этих токов заметно превышает размеры пластины [12].
Неоднородность в виде открытого конца МПЛ (торца антенны) также приводит к дополнительной концентрации электромагнитного поля вблизи открытого конца линии, что эквивалентно увеличению электрической длины линии (Приложение 1), а также к дополнительному излучению.
Одним
из наиболее распространённых подходов к анализу этого излучения является метод
Олинера (Arthur A. Oliner) [40], в
соответствии с этим методом отрезок МПЛ заменяется эквивалентным волноводом с
магнитными боковыми стенками шириной ![]() и заполненного диэлектриком с
проницаемостью
и заполненного диэлектриком с
проницаемостью ![]() . Величины
. Величины ![]() и
и ![]() выбираются из условия равенства
характеристических сопротивлений и постоянных распространения МПЛ и волновода,
эквивалентного по геометрическим параметрам [41].
выбираются из условия равенства
характеристических сопротивлений и постоянных распространения МПЛ и волновода,
эквивалентного по геометрическим параметрам [41].
Поскольку
электромагнитное поле НПЛ сосредоточено в основном в области под токонесущим
проводником и с ростом частоты поле всё более концентрируется в этой области, то
имеет смысл сравнивать свойства НПЛ и прямоугольного волновода. Строго говоря,
продольное волновое число в НПЛ с идеально проводящими проводниками и идеальным
диэлектрическим заполнением есть комплексная величина ![]() [41].
Наличие мнимой части связано с
дифракционным излучением волны из линии [42]. Увеличение емкостной составляющей
концевой проводимости вычисляется через погонную проводимость щели, которая
образована проводящей полуплоскостью, лежащей на слое диэлектрика с экраном.
Выражение для погонной проводимости имеет вид [10]
[41].
Наличие мнимой части связано с
дифракционным излучением волны из линии [42]. Увеличение емкостной составляющей
концевой проводимости вычисляется через погонную проводимость щели, которая
образована проводящей полуплоскостью, лежащей на слое диэлектрика с экраном.
Выражение для погонной проводимости имеет вид [10]
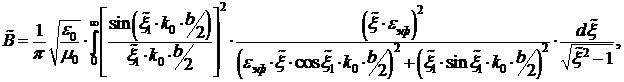
где ![]()
![]() - длина волны в воздухе.
- длина волны в воздухе.
Из этого выражения очевидно, что при ![]() величина
погонной проводимости
величина
погонной проводимости ![]() приобретает комплексное
значение, что соответствует комплексному значению продольного волнового числа. На
графиках, представленных на рис. 17, показано поведение нормированного продольного
числа
приобретает комплексное
значение, что соответствует комплексному значению продольного волнового числа. На
графиках, представленных на рис. 17, показано поведение нормированного продольного
числа ![]() и
и ![]() в
сравнении с волноводом, эквивалентным по геометрическим параметрам
несимметричной полосковой линии. Обозначения даны по [41], или
в
сравнении с волноводом, эквивалентным по геометрическим параметрам
несимметричной полосковой линии. Обозначения даны по [41], или ![]() Здесь же приведены значения продольного
волнового числа прямоугольного волновода с поперечным сечением
Здесь же приведены значения продольного
волнового числа прямоугольного волновода с поперечным сечением ![]() , приведённого к размерам несимметричной
полосковой линии. Наличие дифракционных потерь в несимметричной полосковой
линии приводит к существованию волны в закритичной области (в прямоугольном
волноводе с идеальными проводящими стенками распространение волны в этой
области отсутствует:
, приведённого к размерам несимметричной
полосковой линии. Наличие дифракционных потерь в несимметричной полосковой
линии приводит к существованию волны в закритичной области (в прямоугольном
волноводе с идеальными проводящими стенками распространение волны в этой
области отсутствует: ![]() ).
).
Продольное волновое число не
является характеристикой волн чисто ![]() или
или ![]() типов, а представляет собой характеристику
гибридной Т – волны [42]. Это хорошо видно из графиков отраженных сигналов (рис.
18), принятых на бетонном основании приемным АФУ дециметрового диапазона: для
передающей антенны (рис. 6), излучающей гибридную волну, отражённый сигнал показан
красным; зелёным показан вид отражённого сигнала от излученной волны
типов, а представляет собой характеристику
гибридной Т – волны [42]. Это хорошо видно из графиков отраженных сигналов (рис.
18), принятых на бетонном основании приемным АФУ дециметрового диапазона: для
передающей антенны (рис. 6), излучающей гибридную волну, отражённый сигнал показан
красным; зелёным показан вид отражённого сигнала от излученной волны ![]() («крылья» передающей антенны заменены на
диэлектрические пластины аналогичных размеров, волна
(«крылья» передающей антенны заменены на
диэлектрические пластины аналогичных размеров, волна ![]() в
диэлектрической пластине возбуждается поперечным металлическим штырём).
Характеристики участвующего в измерениях комплекса даны в [31]. Из графиков,
представленных на рис. 20, следует, что амплитуда волны
в
диэлектрической пластине возбуждается поперечным металлическим штырём).
Характеристики участвующего в измерениях комплекса даны в [31]. Из графиков,
представленных на рис. 20, следует, что амплитуда волны ![]() меньше амплитуды гибридной Т-волны (61%,
в [4] приведено 65%), её спектр более высокочастотен, что обусловливает её
быстрое затухание по глубине. Анализ электродинамического приближения приведен
в Приложении 1.
меньше амплитуды гибридной Т-волны (61%,
в [4] приведено 65%), её спектр более высокочастотен, что обусловливает её
быстрое затухание по глубине. Анализ электродинамического приближения приведен
в Приложении 1.
Неоднородная микрополосковая антенна как излучающая симметричная щелевая линия
Поскольку в рассматриваемой антенне одновременно возбуждаются плоские вибраторы в виде металлических (медных) полос и диэлектрическая подложка МПА, то подобные антенны можно одновременно рассматривать и как плоский вибратор с собственным входным сопротивлением и как щелевой излучатель (магнитный вибратор), обладающий таким же сопротивлением, поскольку это одна и та же антенна (так называемый принцип самодополнительности, или комплементарности, введён Ясуто Мушияки, 1948).
Этот принцип гласит: всегда найдётся такой угол поворота, когда металлическая полоска ложится в металлическую, и угол - когда форма щели повторит форму металлической части [43]. В нашем случае принцип комплементарности описывается уравнением (15), задающим размеры поперечных сечений токоведущей линии и щели.
Такой щелевой излучатель представляет собой симметричную
щелевую линию (СЩЛ), вырезанную в металлической плоскости, расположенной на
одной из сторон диэлектрической подложки с металлическим экраном на другой
стороне подложки (рис. 6). Волна ![]() в диэлектрической
пластине возбуждается поперечным по отношению к толщине пластины металлическим
штырём, являющимся продолжением точки запитывания металлических (медных) полос МПА.
Штырь, выходящий со стороны металлического экрана диэлектрической подложки,
электрически развязан с ним.
в диэлектрической
пластине возбуждается поперечным по отношению к толщине пластины металлическим
штырём, являющимся продолжением точки запитывания металлических (медных) полос МПА.
Штырь, выходящий со стороны металлического экрана диэлектрической подложки,
электрически развязан с ним.
К настоящему времени не существует достаточно точной теории
СЩЛ и такого отчётливого физического понимания принципа работы СЩЛ, которое
характерно для НПЛ[20].
При толщине диэлектрика ![]() , где
, где ![]() - длина волны в диэлектрической подложке (
- длина волны в диэлектрической подложке (![]() , рис. 2;
рис. 17) напряжение между краями
протяжённой регулярной щели можно заменить магнитным током (Прил.1). При этом
продольная составляющая магнитного поля записывается в виде уходящей волны [42].
, рис. 2;
рис. 17) напряжение между краями
протяжённой регулярной щели можно заменить магнитным током (Прил.1). При этом
продольная составляющая магнитного поля записывается в виде уходящей волны [42].
![Подпись: Ампл., В
Время, 0.8 нс/точка
Рис. 18 - Отражённый сигнал от гибридной излученной волны, принятый на бетонном основании приемным АФУ дециметрового диапазона [31] (вид передающей антенны - рис.6), показан красным; зелёным показан вид отражённого сигнала от излученной волны («крылья» передающей антенны заменены на диэлектрические пластины аналогичных размеров)](text.files/image204.png)
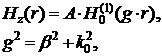
где ![]() -
расстояние от начала координат до точки наблюдения;
-
расстояние от начала координат до точки наблюдения; ![]() - функция
Ханкеля первого рода
- функция
Ханкеля первого рода ![]() – порядка;
– порядка; ![]() - продольное волновое число;
- продольное волновое число; 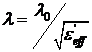 - длина волны в СЩЛ;
- длина волны в СЩЛ; ![]() - волновое число для длины волны в воздухе;
- волновое число для длины волны в воздухе;
![]() - эффективная диэлектрическая
проницаемость СЩЛ, порядок определения дан в [50,
15];
- эффективная диэлектрическая
проницаемость СЩЛ, порядок определения дан в [50,
15]; ![]()
Особого внимания здесь заслуживает замедление волн, составляющих гибридную Т-волну, относительно друг друга: по мере увеличения размера щели фазовый набег между токами проводимости и смещения увеличивается (рис. 14)[21].
Заключение
Задача параметрической оптимизации сверхширокополосности антенны подповерхностного зондирования по компонентам вектора варьируемых параметров типа размеры поперечных сечений токоведущих линий антенны сведена к нахождению решения условия развязки её погонной индуктивности с подстилающей средой.
Неравномерность параметра
![]() матрицы рассеяния антенны (<8.5%) в диапазоне
частот 0.3-700 МГц позволяет оценить сверхширокополосность антенны
подповерхностного зондирования, для которой выполняется условие развязки
её погонной индуктивности с подстилающей средой, как характерную для Т- волн.
матрицы рассеяния антенны (<8.5%) в диапазоне
частот 0.3-700 МГц позволяет оценить сверхширокополосность антенны
подповерхностного зондирования, для которой выполняется условие развязки
её погонной индуктивности с подстилающей средой, как характерную для Т- волн.
На основании результатов, полученных в [40, 42] и приведенных в данной работе экспериментально измеренных частотных характеристик антенны, сделан вывод о том, что у подобных антенн собственное значение продольного волнового числа существует начиная с частот, близких к нулевой частоте.
Основной тип излучаемой волны
- гибридная Т-волна [42], обусловленная продольным распределением тока в
неоднородной МПА. Её гибридность обусловлена содержанием в ней волны типа ![]() , наличие которой доказано
экспериментально. Гибридность может быть обусловлена комплементарностью данной
антенны: на излучение она работает как несимметричная полосковая антенна и, одновременно,
как симметричная щелевая антенна, что вызвано характером её возбуждения.
, наличие которой доказано
экспериментально. Гибридность может быть обусловлена комплементарностью данной
антенны: на излучение она работает как несимметричная полосковая антенна и, одновременно,
как симметричная щелевая антенна, что вызвано характером её возбуждения.
Дальнейшее развитие параметрической оптимизации по компонентам вектора варьируемых параметров типа размеры поперечных сечений токоведущих линий антенны предполагает нахождение решения управления замедлением волн с учётом подстилающей среды.
Частотные особенности
данной антенны в области низких частот позволяют выделять при СШП измерениях
конкретно идентифицируемые признаки: наличие или отсутствие воды (![]() МГц); газовые ловушки (
МГц); газовые ловушки (![]() МГц – радон,
МГц – радон, ![]() МГц -
воздух). Простота и технологичность изготовления делают цену антенны доступной,
а ее массогабаритные характеристики обусловливают легкость транспортировки
всего антенно-измерительного комплекса (работы проводились в США, Европе, странах
ЮВА, Иордании). Особое место занимает простота метрологического обеспечения –
обязательная проверка на работоспособность с помощью измерителя параметров
четырёхполюсника OBZOR-103 практически исключает возможность измерений на
неисправной аппаратуре.
МГц -
воздух). Простота и технологичность изготовления делают цену антенны доступной,
а ее массогабаритные характеристики обусловливают легкость транспортировки
всего антенно-измерительного комплекса (работы проводились в США, Европе, странах
ЮВА, Иордании). Особое место занимает простота метрологического обеспечения –
обязательная проверка на работоспособность с помощью измерителя параметров
четырёхполюсника OBZOR-103 практически исключает возможность измерений на
неисправной аппаратуре.
Электродинамическое приближение
Основное отличие несимметричной полосковой линии от
симметричной состоит в том, что распространяющаяся в ней основная волна
(Т-волна) обладает «волноводным характером», т.е. имеет достаточно заметную
дисперсию. Это обстоятельство особенно сказывается при проектировании и реализации
разнообразных резонансных структур, как например, полосовых фильтров [42].
Продольное волновое число ![]() обладает спектром
собственных значений, состоящим из двух множеств:
обладает спектром
собственных значений, состоящим из двух множеств:
а) конечное множество
дискретных собственных значений, соответствующих конечному числу волн различных
типов, включающее основной тип волны («дискретный» спектр). В нашем случае – 23
(по числу полосок) для антенны типа «![]() »; 9 - для антенны типа
«меандр» (
»; 9 - для антенны типа
«меандр» (![]() ); в монографии «Daniels, D. J. Ground Penetration Radar» их число - 41;
); в монографии «Daniels, D. J. Ground Penetration Radar» их число - 41;
б) последовательность собственных значений, соответствующих полю излучения («непрерывный» спектр излучаемого импульса).
Дискретные волны не являются чисто волнами E- и H-типов, а представляют собой гибридные волны. Поэтому для их определения необходимо решать уравнение Гельмгольца для продольных составляющих поля:
 , (П.1)
, (П.1)
где 
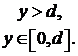
В плоскости y=0 продольные составляющие поля должны удовлетворять следующим граничным условиям:
![]() ,
, ![]() (П.2)
(П.2)
На границе «подложка – пространство» тангенциально составляющие поля должны быть непрерывны:

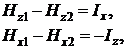 (П.3)
(П.3)
где индекс 1 относится к области y>d, а индекс 2 – к области подложки, т.е. ![]() . Полосковый проводник заменяется
неизвестным эквивалентным распределением тока, равным
. Полосковый проводник заменяется
неизвестным эквивалентным распределением тока, равным
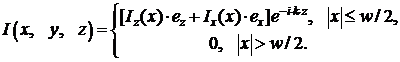
После применения
комплексного преобразования Фурье к (П.1) и перехода от действительной
переменной ![]() к комплексному волновому числу
к комплексному волновому числу ![]() , необходимо удовлетворить условиям (П.2)
и (П.3).
, необходимо удовлетворить условиям (П.2)
и (П.3).
Для полоскового
проводника граничные условия можно записать следующим образом (![]() ):
):
![]()
![]()
Эти условия, применимые
только для действительных значений переменной ![]() ,
приводят к интегральному уравнению, связывающему распределение токов
,
приводят к интегральному уравнению, связывающему распределение токов ![]() и
и ![]() , для
каждого собственного значения продольного волнового числа
, для
каждого собственного значения продольного волнового числа ![]() :
:

где функции ![]() и
и
![]() есть комплексные преобразования Фурье
неизвестных составляющих тока
есть комплексные преобразования Фурье
неизвестных составляющих тока ![]() и
и ![]() . Полное решение этого уравнения дает
бесконечное число возможных дискретных типов волн, но на каждой данной частоте
существует только конечное число волн различных типов.
. Полное решение этого уравнения дает
бесконечное число возможных дискретных типов волн, но на каждой данной частоте
существует только конечное число волн различных типов.
Для его решения существует несколько методов, выбор которых определяется необходимой точностью расчета. Так, если необходимо рассмотреть только основной тип гибридной волны, то можно использовать метод спектрального разложения [45].
Расчет, проведенный в [46]
для четырех высших типов волн, основывается на предположениях, что поперечная
составляющая тока ![]() пренебрежимо мала и заряд в
полосковом проводнике распределен согласно функции Максвелла [42]. Тогда
применение комплексного преобразования Фурье приводит к тому, что функции
распределения тока
пренебрежимо мала и заряд в
полосковом проводнике распределен согласно функции Максвелла [42]. Тогда
применение комплексного преобразования Фурье приводит к тому, что функции
распределения тока ![]() , соответствующие высшим типам
волн, описываются функциями Бесселя первого рода.
, соответствующие высшим типам
волн, описываются функциями Бесселя первого рода.
Ещё более точное решение можно получить в случае, когда составляющие тока после применения комплексного преобразования Фурье представляются полиномами Лежандра либо Чебышева [47], [48].
Таким образом, поскольку
в НЛП распространяется не чистая Т-волна, то волновое сопротивление линии и
эффективная диэлектрическая проницаемость подложки изменяются с изменением
частоты. Существует несколько возможных путей учета дисперсии в НЛП. Например,
в результате решения интегрального уравнения, связывающего распределение токов ![]() и
и ![]() , получено,
что дисперсия приводит к изменению значения постоянной распространения основного
типа волны по следующему закону [49]:
, получено,
что дисперсия приводит к изменению значения постоянной распространения основного
типа волны по следующему закону [49]:
![]() ,
,
где
![]()
![]() - постоянная распространения,
полученная в Т-приближении [50, 51] с погрешностью в определении эффективной
диэлектрической проницаемости подложки
- постоянная распространения,
полученная в Т-приближении [50, 51] с погрешностью в определении эффективной
диэлектрической проницаемости подложки![]() [51],
изменение которой по частоте учитывает дисперсию в НЛП.
[51],
изменение которой по частоте учитывает дисперсию в НЛП.
Литература
1. Proceedings of the Ultra-Wideband, Short-Pulse Electromagnetics, 5. – New York: Kluwer Academic/Plenum Publishers, 2002. – 751 p.
2. Schantz H. The Art and Science of Ultra-Wideband Antennas. − Boston, London: Artech House, 2005. − 331 p.
3. Иммореев И.Я., Синявин А.Н. Излучение сверхширокополосных сигналов. – Антенны, 2001, № 1 (47), с. 8 -16.
4. Беличенко В.П., Якубов В.П., Запасной А.С. Использование особенностей формирования поля ближней зоны комбинированной антенны для улучшения её характеристик широкополосности // Труды III Всероссийской конференции «Сверхширокополосные сигналы в радиолокации, акустике и связи» - М.: 2010, с. 247 -251.
5. Федянович В.И. О предельной широкополосности излучателей. // Антенны. – 2008. – Вып. 1 (128). – С. 3-17.
6. Tefiku F., Grimes C.A. Coupling between elements of electrically small compound antennas // Microwave and Optical Technology Letters. – 1999. – V. 22. – No 1. – P. 16-21.
7. da Costa K.Q., Dmitriev V. Combination of electric and magnetic dipoles with single element feeding for broadband application // MOTL. − 2006. − V. 48. − No. 1. − P. 8–11.
8. Неганов В.А., Клюев Д.С., Медведев С.В. Функционал входного сопротивления тонкого электрического вибратора // Письма в ЖТФ, 2001 , т. 27, вып. 21, с. 29 - 34.
9. Неганов В.А., Корнев М. Г., Матвеев И. В. Новое интегральное уравнение для расчёта тонкого электрического вибратора // Письма в ЖТФ, 2001 , т. 27, вып. 4, с. 62-73.
10. Электродинамический расчет характеристик излучения полосковых антенн / Б.А. Панченко, С.Т. Князев, Ю.Б. Нечаев, В.И. Николаев, С.Н. Шабунин.- М.: Радио и связь, 2002. -256 с.
11. Чебышев В.В. Интегральное уравнение Фредгольма 1-го рода для тока узкого полоскового вибратора и численный метод его решения. – Машинное проектирование устройств и систем СВЧ. – М.: 1979, с. 204 – 215.
12. Марков Г.Т., Сазонов Д.М. Антенны. - М.: Энергия, 1975, -528 с.
13. Черноусов В.С. Нестационарное излучение антенных систем. – Радиотехника и электроника, 1965, № 8, с. 87-94.
14. Балакирев В.А., Гладков В.С., Синельников Г.Л. Формирование электромагнитных импульсов апертурными антеннами. – Электромагнитные явления, т.1, №4, 1998, с. 522 – 537.
15. Ковалев И.П., Пономарёв Д.М. Анализ процессов излучения и приёма импульсных сигналов во временной области. – М.: Рикел, Радио и связь, 1996. -112 с.
16. Малютин Н.Д. Многосвязанные полосковые структуры и устройства на их основе. – Томск: Из-во Том. ун-та, 1990. – 164 с.
17. Schelkunoff S.A. A conversation of Maxwell’s equations into generalized telegraphist’s equations. - BSJ, 1955, v. 34, № 5, 995 p.
18. Chang Fung-Yuel. Transient analysis of losstess coupled microstrip arrays in an inhomogeneous dielectric medium. – IEEE Trans. in MTT.1970, v. MTT-18. № 9, pр. 616 – 626.
19. Rizzoli V. The calculation of scattering parameters of coupled microstrip arrays of any cross section. Alta Freq., 1973, v. 49, № 4, pp. 191 -199.
20. Кравченко С.И., Бахарев С.И. Расчёт матрицы рассеяния многопроводных полосковых линий и устройств на их основе. – Вопросы радиоэлектроники. Сер. ОТ, 1978, вып. 8, с. 45 – 53.
21. Arndt F. Andwendung der Ahnlichkets – transformation bie Microstrip – leiungen. – NTZ, 1973, № 3, pp. 46 -49.
22. Карпуков Л.М. Анализ элементов и устройств СВЧ на многопроводных связанных микрополосковых линиях. – Ив. Вузов СССР. Радиоэлектроника, 1981, № 3, с. 60 - 63.
23. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. –М.: Энергия, 1975, - 750 с.
24. Справочник по элементам волноводной техники / Фельдштейн А.Л., Явич Л.Р., Смирнов В.П.. – М.: Сов. радио, 1967. – 552 с.
25. Чебышев В.В. Антенны и устройства СВЧ. Микрополосковые излучатели и решетки в слоистой среде /В.В. Чебышев // М.: Радиотехника, 2003.- 102 с.
26. Alexopoulos N.G., Rana I.E. On the solution to Pochngtones equation for antennas printed on grounded substrates – Int. Symp. Dig. – Antennas and Propag. Seattle, Mash, 1979, v.1, pp. 171 -174.
27. Rana I.E., Alexopoulos N.G. Current distribution and input impedance printed dipoles – IEEE Trans, 1981, v. AP 29, № 1, pp. 99 – 105.
28. Microstrip Antennas, published in Electrical and Electronic Engineering, Edited by Nasimuddin Nasimuddin, ISBN 978-953-307-247-0, Number of pages 540, 2011, Published by InTech.
29. Справочник по расчёту и конструированию СВЧ полосковых устройств / С.И. Бахарев, В.И. Вольман, Ю.Н. Либ, Н. М. Мамонова, А.Д. Муравцов, А.Г. Саркисьянц, Р.А. Силин, О.А. Славинский, Д.Д. Ширяев. Под ред. В.И. Вольмана. – М.: Радио и связь, 1982. – 328 с.
30. Carlin H.J. A simplified circuit model for microstrip. - IEEE Trans. on MTT, 1973, v. MTT-21, № 9, pp. 589 – 591.
31. Болтинцев В.Б., Ильяхин В.Н., Безродный К.П. Метод электромагнитного импульсного сверхширокополосного зондирования подстилающей среды // Журнал радиоэлектроники хэлектронный журнал].- 2012. - N1. - URL: http://jre.cplire.ru/jre/jan12/14/text.pdf. - 39 с.
32. Кац Б.М., Мещанов В.П., Фельдштейн А.Л. Оптимальный синтез устройств СВЧ с Т-волнами. – М.: Радио и связь, 1984. – 228 с.
33. Красюк Н.П., Дымович Н.Д. Электродинамика и распространение радиоволн. М., «Высш. школа», 1974. -536 с.
34. Калантаров П.Л., Цейтлин Л.А. Расчёт индуктивностей: Справочная книга. Л.: Энергоатомидат, 1986. - 488 с.
35. Свидетельство на полезную модель № 28289. Российская Федерация 7 H 01 Q 7/00. Антенна для подповерхностного зондирования / Болтинцев В.Б.; заявитель и патентообладатель ЗАО НПФ Геодизонд. № 2002126446/20; заявл. 07.10.02; опубл. 10.03.03, Бюл.№7. - М.: 2003.- 4с.
36. Абденов А.Ж., Мальцев А.С., Рубинович М.Г. Оценка погрешности методов расчёта индуктивности элементов в микрополосковом исполнении. – ВЕСТНИК АлтГТУ им. И. И. Ползунова, № 2, 2006, с. 162 -168.
37. Капралов Г.Н, Бичурин М.И. , Фомин О.Г., Татаренко А.С. Сверхширокополосная согласованная нагрузка // Вестник Новгородского государственного университета, 1999, №13. – 4 с.
38. Глухова О.Е., Креницкий А.П., Мещанов В.П., Салий И.Н. Шлейфовые трансформаторы сопротивлений на канонических нерегулярных линиях передачи// Вопросы прикладной физики. 2006. Вып. 13. –с. 66 -69.
39. Фролов А.Д. Электрические и упругие свойства мёрзлых пород и льдов. Пущино: ОНТИ ПНЦ РАН, 2005. -607 с.
40. Нефёдов Е.И., Фиалковский А.Т. Полосковые линии передачи. Теория и расчёт типичных неоднородностей. – М.: Наука, 1974. – 128 с.
41. Зайцев С.В., Фиалковский А.Т. Краевые эффекты в полосковых структурах при произвольном угле скольжения волны. – Изд. Вузов: Радиофизика – 1981, т. 24, № 9, с. 1152-1158.
42. Гвоздев В. И., Нефёдов Е.И. Объёмные интегральные схемы СВЧ. – М.: Наука, 1985.- 247 с.
43. Антенно-фидерные устройства и распространение радиоволн: Учебник для вузов / Г.А. Ерохин, О.В. Чернышев, Н.Д. Козырев, В.Г. Кочержевский; Под. ред. Г.А. Ерохина. – 2-е изд., испр. – М.: Горячая линия–Телеком, 2004. – 491 с.
44. Denlinger E.J. Losses of microstrip lines. –IEEE Transactions on Microwave Theory and Techniques, Vol. MTT-28, No. 6, Jun 1980, pp. 513-522.
45. Itoh T., Mittra R. Spectral-domain approach for calculating the dispersion characteristics of microstrip lines/ - IEEE Trans. MMT, 1973, v. 21, № 7, рp. 496 -499.
46. Van de Capelle A.R., Luypaert P.J., Lenken K.U. A computer analysis of the discrete mode spectrum open microstrip transmission lines. – In: Proc. IEEE Int. Microwave Symp., 1978, pp. 413 -415.
47. Kuester E. f., Chang D. C. Some recent theoretical studies on open microstrip. - In: Proc. IEEE Int. Microwave Symp., 1979, pp. 325 -328.
48. Заргано Г.Ф., Лерер А.М., Ляпин А.М., Синявский Г.П. Линии передачи сложных сечений. - Ростов-на-Дону: Изд-во РГУ, 1983. - 320 с.
49. E. Yamashita, K. Atsuki and T. Ueda, “An Approximate Dispersion Formula of Microstrip Lines for Computer Aided Design of Microwave Integrated Circuits”, IEEE Trans Microwave Theory and Techniques, vol. 27, pp. 1036-1039,
1979.
50. Getsinger W. J. Dispersion of parallel-coupled microstrip.- IEEE Trans. Microwave Theory Tech., vol. MTT-21, 1973, pp. 144 - 145.
51. Kirschning M., Jansen R. H. Accurate Wide-range Design Equations for The Frequency-Dependent Characteristic of Parallel Coupled Microstrip Lines. - IEEE Trans. On micro wave theory and techn. 1984, v. MTT-32, № 1, pp. 83 -90.
[1] Механизмы повреждения либо деградации свойств полупроводниковых элементов под действием ЭМИ мы здесь не рассматриваем.
[2] Болтинцев В.Б., Ильяхин В. Н., Безродный К.П. Сверхширокополосная георадиолокация: успехи и проблемы // Записки Горного института. 2011, т. 194. - С.132-137.
[3] Болтинцев В. Б., Ильяхин В. Н., Салихов Р.М. Применение метода электромагнитного импульсного сверхширокополосного (ЭМИ СШП) зондирования на стадии разведки месторождения горючих сланцев в Иордании/ // Записки Горного института. 2011, т. 194. - С.138-145.
[4] Аналогичные работы по импульсным генераторам большой амплитуды ведутся в Нижегородском политехническом университете (феррит - тиристорный генератор), в г. Томске в Институте прикладной электроники (генератор на базе GaAs), в г. Троицке Московской области в ИЗМИРАНе (генератор на водородном разряднике - слайсер). За рубежом генераторы такого класса разработаны на базе полевых MOSFET – транзисторов.
[5] Месторождение Боковое, Республика Саха (Якутия). Работы отличались получением «цифры» отражённого из подповерхностной среды радиолокационного сигнала в полевых условиях. Ранее на комплексах типа 17-ГРЛ-1 (разработка Института горного дела Севера ЯФ СО АН СССР), применяемых в Якутии, сигнал либо зарисовывался, либо фотографировался.
[6] Пат. № 2144682. Российская Федерация 7 G 01 S 13/02. Способ радиолокационного зондирования геологического разреза / В. Б. Болтинцев; заявитель и патентообладатель Болтинцев В.Б. - №99104111/09; заявл. 01.03.1999; опубл. 20.01.00, Бюл.№ 2. – М.: 2000.- 12 с.
[7] Определяется величиной поверхностной проводимости, ёмкостью поглощения органическими коллоидами; дипольной поляризацией за счёт ориентации органических коллоидов в сильном электромагнитном поле и процессами ионно – релаксационной поляризации.
[8] Здесь можно выделить такие антенны, как Impulse Radiating Antennas, Vivaldi Antennas, Scissor – Antennas, ТЕМ - антенны. Их параметры и электродинамические характеристики весьма обстоятельно представлены в [1, 2].
[9] Не следует забывать, что применение сложных численных методов имеет свою «цену» и может быть весьма затратным как по времени, так и по стоимости. Более того, численное моделирование в полном смысле этого слова включает в себя не только расчеты электродинамических параметров, но и ряд других вопросов, включая оптимизацию системы/проекта в целом. Тем не менее, рано или поздно этим приходится заниматься. При этом следует предостеречь пользователя от применения некоторых «универсальных» моделирующих программ, недостаточно приспособленных для моделирования поведения структур со сложными индуктивными связями.
[10] См. также: Качественная оценка вычислительных методов электродинамики на примере программных продуктов для высокочастотного моделирования микрополосковых антенн / А. Васильченко, И. Скольц, В. де Раад, Г. Ванденбош // Технологии в электронной промышленности , № 3, 2008. – С. 52-56.
[11].См. также: Неганов В.А., Табаков Д.П., Яровой Г.П. Современная теория и практические применения антенн. -М.: Радиотехника, 2009. – 720 с.
[12] Ранее они назывались ТЕМ – волнами (здесь придерживаемся ГОСТ 18238 – 72. Линии передачи СВЧ: Термины и определения).
[13] Известное условие Хевисайда - , которое равнозначно равенству . Линию, удовлетворяющую таким требованиям, называют линией без искажений [23].
[14] Очевидно, что при учёте подстилающей среды входной импеданс антенны изменится на величину взаимного импеданса между антенной и её зеркальным отражением [12].
[15] Безродный К. П., Беспалов П.Н., Болтинцев В.Б. Разработка технологии радиолокационного обследования бетонных и железобетонных конструкций с целью обнаружения скрытых нарушений сплошности бетона (трещин и трещинных зон, разуплотненных участков), создание автоматизированного измерительного комплекса // Деп. в ВНТИЦ 26.01.2004, № 01.200 315448 (Каталог НИОКР РФ 2010, приборостроение). -СПб., 2004.-72c.
[16]Антенна аналогичного вида в устройстве для поиска мин приведена на с.151-152 в Daniels, D. J. Ground Penetration Radar. – 2004; The Institution of Electrical Engineers, London. UK.-723 p.
[17] Порядок анализа дан в соответствии с тем, как он проведен в [8], [12].
[18] По экспериментальным данным (Ахадов Я. Ю., 1972; Хиппель А.Р., 1959; Тонконогов М.П., Векслер В.А., Биржанов К.Ж., 1975; Семихина Л. П., 2007) частота резонанса воды ~25МГц.
[19] Безродный К. П., Болтинцев В.Б., Ильяхин, В. Н. Оценка обводненности горной выработки по данным электромагнитного импульсного сверхширокополосного зондирования // Жилищное строительство. -2011, №9. – С.34-37.
[20] Клюев С. Б. , Нефедов Е. И. , Цзи У. Несимметричная двойная щелевая линия// Физика волновых процессов и радиотехнических систем. -2009, т. 12, №4. – с.44-51.
[21] Для справки: «замедление» для волны прямоугольного волновода составляет 2.8: поперечное сечение Волна при тех же условиях не распространяется.
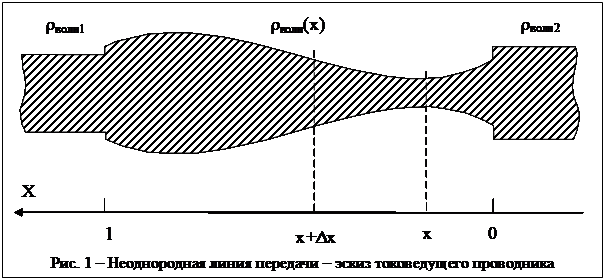
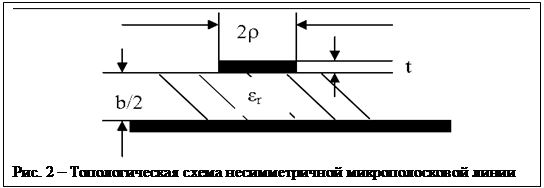
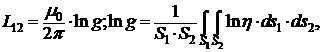

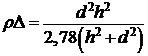


![Подпись:
Рис. 17 - Сравнение действительной и мнимой составляющих волнового числа одинаковых по геометрическим соотношениям несимметричной полосковой линии и прямоугольного волновода [33]](text.files/image197.png)