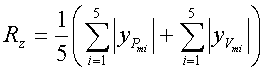УДК 620.01.08

Практическое применение методов фрактального анализа

С. З. Ихлазов

Омский государственный технический университет, радиотехнический факультет

 

Получена 9 марта 2012 г.

 

Аннотация. Приводятся результаты исследования применения методов фрактального анализа для классификации сигналов различного происхождения. Первая группа сигналов была получена с датчика вибраций авиационного двигателя, вторая – это профилограммы поверхностей бумаг. Исследования проводятся с целью изучения возможности идентификации сигналов методами, основанными на комбинированном применении показателя фрактальной клеточной размерности и стандартных статистических параметров.

Ключевые слова: вибрация, диагностика, идентификация, размерность, сигнал, шероховатость.

Abstract. Results of research of application of methods of the fractal analysis for classification of signals of a various origin are given. The first group of signals has been received from the sensor of vibrations of the aviation engine, the second are profilograms of surfaces of papers. Researches are carried out for the purpose of study of possibility of identification of signals by the methods based on combined application of an index of fractal cellular dimensionality and standard statistical parameters.

Keywords: vibration, diagnostics, identification, dimensionality, signal, roughness.

Введение

В первой части работы, проверяются возможности применения методов фрактального анализа к сигналам, полученным с датчика вибрации. Объектом послужили 13 сигналов, представляющих собой выборки данных, полученные с датчика вибраций самолетного двигателя, который проходил полетные испытания. Достоверно известно, что первый файл представляет полет, проходящий в штатном режиме, т.е. параметры виброданных в пределах нормы – двигатель исправен. Также известно, что 13-й файл – это данные с последнего, аварийного полета, где испытание было прервано по каким-то кардинальным причинам (рис.1), а остальные 11 файлов представляют промежуточные, между этими крайними значениями полеты, отражающие динамику разрушения двигателя.

 

 

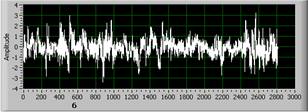
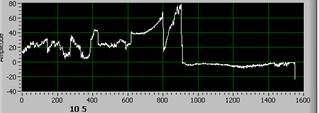
Сигнал 1                                                             Сигнал 13

 

Рис. 1. Граничные сигналы: 1 – норма, 2 – аварийный.

 

Во второй части работы проведены исследования по анализу качества поверхности бумаг с  различной шероховатостью, используемых в полиграфии.

Для исследования были взяты 28 бумаг с разной степенью шероховатости, начиная от 0,222 мкм – 9 образец и заканчивая 5,11 мкм – 27 образец.

 

Описание методики исследования

Цель проведения исследования: изучить возможность классификации сигналов с помощью методов, комплексно использующих фрактальные и статистические параметры. Выяснить, позволяют ли приведенные методы реализовать дальнейшую задачу диагностирования исследуемых объектов. Определить, какие методы лучше использовать для классификации сигналов.

В общем случае, методики сводятся к нахождению комплексной величины, отражающей микро- и макро- неровности сигнала. Эта величина рассчитывается различными способами, используя фрактальную клеточную размерность Dc и статистические параметры Ra и Rz, относящиеся к шероховатости и описанные ниже.

Для нахождения Dc использован метод, описанный в [1], где он применялся для измерения длины природного фрактального объекта, береговой линии Норвегии, по топографической карте. В представленных ниже методиках этот метод использован с некоторыми доработками и ограничениями. Для его реализации исследуемые сигналы были подготовлены, как описано ниже.

Для автоматизированного нахождения фрактальной клеточной размерности было использовано программное обеспечение (ПО), описанное в [2], которое считывает данные из указанного файла и анализирует их по заданному алгоритму, находя значение Dc. Дальнейшие расчеты производятся с помощью электронных таблиц Excel.

 

Описание метода нахождения фрактальной клеточной размерности Dc.

Первый этап: подготовка сигнала.

В ПО задается длина сигнала в единицах измерения (Length), ограничение по максимальному количеству накладываемых сеток (Limit), и массив исследуемых данных.

Затем, находится количество элементов массива (n), размер шага между отсчетами (Shmin=L/n). Находится количество таких шагов входящих в размах сигнала (Sh). Если шагов входит больше, чем указано в значении Limit, то производится ограничение до этого значения, если  меньше – то до расчетного значения Sh. После этого находится минимальный размер ячейки при наложении заданного количества сеток – Size hutch.

Второй этап: производится анализ данных по следующему алгоритму:

А) Вычисляется текущий размер ячейки сетки (hutch), равный размаху, деленному на номер итерации: R/1, R/2, R/3 … R/Sh=hutch.

Б) Сигнал покрывается сеткой с квадратной ячейкой со стороной равной hutch.

В) Подсчитывается количество ячеек, в которое попало хотя бы одно значение из выборки сигнала, и заносится в выходной массив q.

Г) Пункты Б, В повторяются для каждого значения hutch, пока выполняется неравенство hutch ≥ Shmin.

Далее, находится десятичный логарифм каждого значения массива q и массива k (последовательность 1,2,3…n).

Затем, находится коэффициент наклона кривой q, который и является значением Dc.

Ограничения метода.

Перед нахождением Dc необходимо провести исследование группы сигналов на величину минимального размера ячейки Shmin. Если величина Shmin получается меньше единицы, то необходимо масштабировать сигнал по оси абсцисс, т.к. ячейка сеток квадратная, а выборка данных представляется в виде массива с элементами, увеличивающимися на единицу. Таким образом, при ячейке со стороной меньше 1, теоретически получается, что ячейка попадает между отсчетами, что приводит к ошибке метода. Соответствующие исследования были проведены для одной группы сигналов – сигналов с вибродатчика. Зависимость значений Dc от множителя представлены на рис.2.  В эксперименте использовались значения Dc при множителе 100.

 

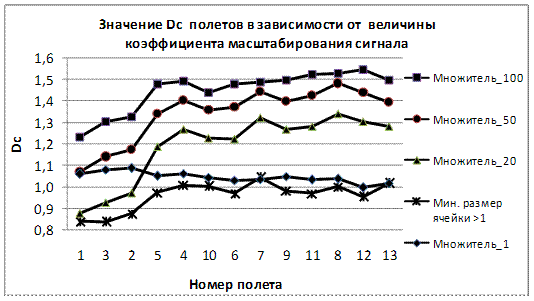
Рис. 2. Зависимость Dc от значения множителя.

 

Следующим этапом, производится сравнение двух методик для анализа вибросигналов. Для этого, находится значение высоты неровностей сигнала по десяти точкам Rz [3], которое равно сумме средних арифметических (абсолютных) отклонений точек пяти наибольших максимумов и пяти наибольших минимумов данных в пределах длины сигнала.

,

где y_Pmi – отклонение пяти наибольших максимумов сигнала; y_Vmi – отклонение пяти наибольших минимумов сигнала.

После нахождения этих двух величин выполняются вычисления по следующим формулам:

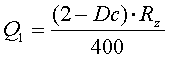,                                           (1)

 

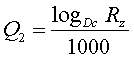,                                                (2)

где деление на константу введено для масштабирования графиков на рис.3.

Для сравнения классификационных возможностей, получившиеся зависимости коэффициентов Q₁, Q₂ и Rz от номера полета, представлены на графике (рис.3).

 

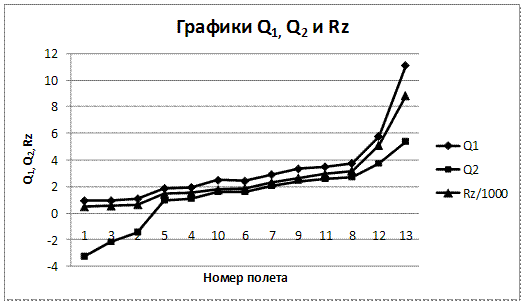
Рис. 3. Сравнение стандартной величины Rz и коэффициентов Q₁ и Q₂.

 

При детальном рассмотрении полученных кривых видно, что стандартная величина Rz, показывающая размах сигнала, не может  идентифицировать сигналы с равной амплитудой, но разной плотностью неровностей (сигналы 1,2,3 (рис.4)).

Коэффициент Q₁ практически полностью совпадает с Rz и имеет те же недостатки, что и  величина Rz. (Ранее, данный метод был исследован для оценки качества поверхности бумаг и описан в [4]). 

Коэффициент Q₂ справляется с задачей разделения сигналов с равной амплитудой лучше, чем Rz и Q₁, опираясь при этом на показания фрактальной клеточной размерности. Данная особенность отлично видна на первых трех сигналах (рис.4), имеющих примерно одинаковую амплитуду.  

 

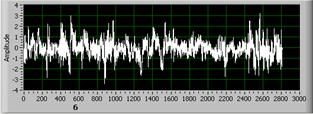
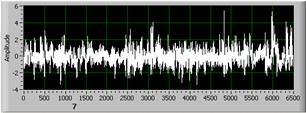
Сигнал 1                                                                   Сигнал 2

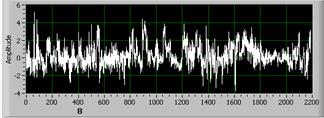
Сигнал 3

 

Рис. 4. Нормальные сигналы, равные по амплитуде, разные по Dc .

 

Результаты исследования вибросигналов

Проведя анализ вибросигналов с помощью методик, описанных выше, получилось, что оба коэффициента Q₁ и Q₂ определяют граничные полеты (1 и 13), но чувствительность этих методов различна. Коэффициент Q₁ больше подвержен влиянию параметра Rz и на графике (рис.3) почти полностью совпадает с графиком Rz, т.е. при таком вычислении (формула 1) и разности в абсолютных величинах, влияние фрактальной клеточной размерности Dc на Rz полностью перекрывается значениями показателя Rz. Коэффициент корреляции рядов Rz и Q₁ равен 0,997, а рядов Q₁ и Dc – 0,52.

При нахождении коэффициента Q₂ происходят вполне видимые изменения в построении упорядоченного ряда (рис.3). Это можно объяснить, опираясь на определение логарифма: логарифм числа b по основанию a определяется как показатель степени, в которую надо возвести основание a, чтобы получить число b. Т.е. значение степени, в которую нужно возвести показатель фрактальной клеточной размерности, чтобы получить число Rz и есть показатель Q₂. Коэффициент корреляции рядов Q₂ и Rz равен 0,84, а рядов Q₂ и Dc – 0,9.

Однако нужно отметить, что если сигнал содержит ярко выраженные одиночные «всплески» (рис.5), то влияние величины Dc сокращается, и определяющим параметром становится величина Rz. Это происходит, потому что значение величины Dc уменьшается незначительно, а значение величины Rz увеличивается заметно. Кроме того, из-за одиночного «всплеска» площадь покрытия сигнала сеткой увеличивается, а основной сигнал на таком уровне отсутствует. И если внимательно проанализировать алгоритм нахождения Dc, то становится понятно, что при увеличении размаха увеличивается размер минимальной ячейки и, соответственно, уменьшается чувствительность метода.

 

    

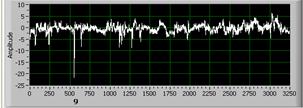
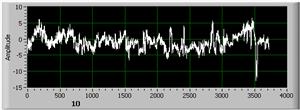
Сигнал 4                                                                  Сигнал 5

   

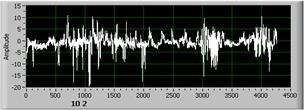
Сигнал 6                                                                 Сигнал 10

 

Рис. 5. Сигналы с помехами типа «всплеск».

 

На рис. 2 представлена зависимость показателя Dc от сигнала, где хорошо видно, что фрактальная клеточная размерность адекватно реагирует (относительно ранжирования по Rz) на сигналы, имеющие более-менее равномерное распределение значений (сигналы 1,2,3,6,10). Сигналы, имеющие одиночные «всплески», «выпадают» из увиденной закономерности и стоят на 3-4 места дальше, если производить упорядочивание по Dc.

При этом нужно помнить об исключениях для логарифма и, соответственно, для данных при вычислении: основание не может быть равно 1 и должно быть больше нуля, число же должно быть строго больше нуля.

Пример классификации сигналов с вибродатчика по значению показателя Q₂ приведен на рис.6. На графике четко можно выделить «нормальные» и «аварийные» полеты. Границы «удовлетворительных» и «неудовлетворительных» полетов проставлены условно, для более точного разделения необходимо провести анализ большего количества данных.

 

 

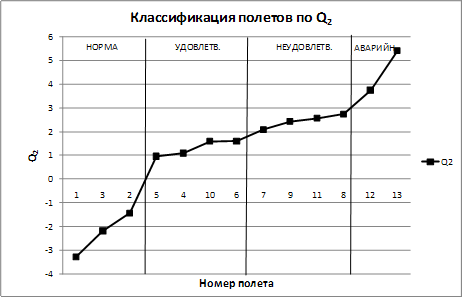
Рис. 6. Пример классификации полетов по значению Q₂ .

 

Анализ качества поверхности бумаги

Следующим этапом производится анализ качества поверхности бумаг. Для этого используется значение Dc, нахождение которого описано выше и статистический параметр Ra, описанный в ГОСТ 2789-73 [3] «Шероховатость поверхности. Параметры, характеристики и обозначения». Стандарт распространя­ется на шероховатость поверхности изделий независимо от их материала и способа изготовления (получения поверхности). В стандарте установлен перечень параметров, которые должны применяться при установлении требований и контроле шерохо­ватости поверхности, также даны общие указания по установле­нию требований. Параметр Ra определяется в ГОСТ 2789-73 как наиболее предпочтительный при описании неровности поверхности материала.

По стандарту шероховатость поверхности определяется как со­вокупность неровностей поверхности с относительно малыми ша­гами, выделенная с помощью базовой длины.

Суть метода заключается в нахождении значения Dc профилограммы (рис.7), интересующего материала, и стандартного параметра Ra [3]. Дальнейшего вычисления качества поверхности по формуле

,                                                 (3)

где Ra – среднеарифметическое отклонение профиля в пределах базовой длины

,

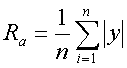где n – число выбранных точек профиля на базовой длине.

 

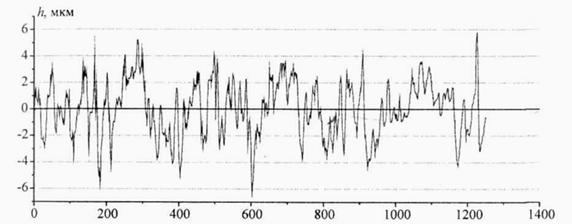
Рис. 7. Профиль мелованной бумаги.

 

Проведя анализ значений Ra (рис.8) видно, что значение стандартного параметра активно реагирует на изменение размеров неровностей профиля поверхности, но на графике есть горизонтальный участок, показывающий, что на поверхностях, имеющих малый размер неровностей этот параметр не информативен, возможно, это указывает на аппаратное ограничение профилографа. Так же можно отметить нечувствительность параметра Ra для дифференцирования профилей с разной степенью изрезанности, имеющих одинаковое значение Ra.

 

Рис.8. Упорядочивание профилограмм по Ra.

 

Для устранения вышеописанных недостатков, дополнительно с параметром Ra был применен параметр Dc, отражающий размерность того пространства, которое занимает множество (профилограмма). На рис.9 показано, что параметр Q₃, использующий совместно с Ra значение Dc, более чувствителен на малых неровностях. При упорядочивании бумаг по Q₃, график получается более крутой и монотонный.

 

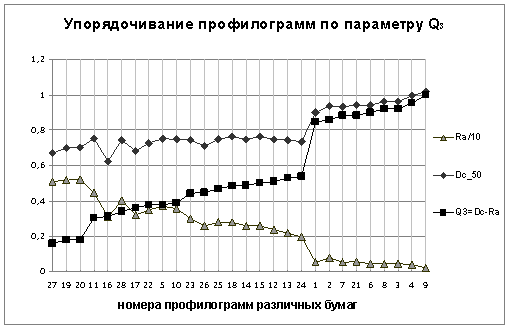
Рис. 9. Упорядочивание профилограмм по Q₃.

 

Значение Q₃, позволяет оценить качество поверхности исследуемой группы печатных материалов и произвести их классификацию, например, по параметру норма, удовлетворительно, неудовлетворительно (Рис.10).

 

Рис. 10. Пример классификации бумаг по значению Q₃.

 

Выводы

1.                Показатель Q₁ имеет коэффициент корреляции с показателем Rz 0,997, а с Dc – 0,52. Это говорит о том, что величина Dc при вычислении Q₁, практически не влияет на конечный результат, и, следовательно, ее использование в таком виде не эффективно.

2.                Коэффициент корреляции Q₂ с показателем Rz 0,84, а с Dc – 0,9. Это отражает обоюдное воздействие двух величин на конечный  результат Q₂. И позволяет произвести классификацию исследуемых сигналов на «нормальные», «удовлетворительные», «неудовлетворительные» и «аварийные».

3.                Показатель Q₃ показывает равномерную чувствительность к изменениям шероховатости поверхности бумаги, что позволяет производить ее качественную классификацию.

4.                Для целей классификации сложных сигналов использование только стандартных параметров Ra и Rz представляется затруднительным. Это связано с их ограничениями по чувствительности к тем или иным изменениям сигнала.

5.                Фрактальная клеточная размерность Dc, при анализе сигналов, помогает разделять сигналы равной амплитуды, но с разной интенсивностью изменения значений. Однако она не способна адекватно реагировать на стабильные сигналы с одиночными «всплесками».

6.                Совместное использование величин Ra, Rz и Dc показало свою эффективность при определенной комбинации, суть которой сводится к максимальному использованию полезных свойств каждой величины. Так, значение Ra показывает среднеарифметическое отклонение сигнала от средней линии, Rz активно откликается на изменение размаха сигнала, значение Dc отражает плотность заполнения этого размаха, т.е. изрезанность сигнала.

7.                На основании проведенных исследований, можно утверждать, что предложенные методики комплексного использования классического и фрактального анализа могут быть применены для идентификации и  классификации сложных сигналов.

 

Литература

 

1.                Федер Е. Фракталы. Пер. с англ. – М.: Мир,1991. – 254с.

2.                Программа определения фрактальной размерности полиграфических материалов. / А.В. Голунов, Л.Г. Варепо, С.З. Ихлазов. – М.:  ОФЕРНИО, 2010. - № 50201001494.

3.                ГОСТ 2789–73 Шероховатость поверхности. Параметры и характеристики. Дата введения 01.01.75 – М.: Стандартинформ, 2006. – 6с.

4.             Определение качества поверхности бумаги методом фрактального анализа / В.Ю. Кобенко, С.З. Ихлазов, А.В. Голунов // Омский научный вестник. – Омск: Изд-о ОмГТУ, 2011. – №3. – С.330-334.