УДК 621.396.67

СНИЖЕНИЕ ЗАМЕТНОСТИ АНТЕНННЫХ СИСТЕМ В РАДИОТЕХНИЧЕСКИХ КОМПЛЕКСАХ КОСМИЧЕСКОГО БАЗИРОВАНИЯ

Ю. Н. Горбунов¹, В. А. Гончаров^2
1 ФГУП «ЦНИРТИ им. академика А.И. Берга», Москва

 ² ОАО «ИМЦ Концерна «Вега», Москва

Получена 5 марта 2012 г. 

 

Аннотация. В статье введены понятия пространственных частот и пространственно-временных фильтров. Приведена оценка возможности использования стохастических режимов управления параметрами фазированных антенных решеток (ФАР) космического базирования.  Обобщены результаты экспериментальных исследований работы адаптивной ФАР в режимах диаграммообразования и стохастической модуляции весовых коэффициентов.

Ключевые слова: космические аппараты, измерение пеленга, антенная система, пространственно-временной фильтр, стохастическая модуляция.

Abstract. Notions of the spatial frequencies and space-temporary filter are entered in article. The assessment of the possibility of using stochastic modes of control of the parameters of space-based phased antennas array is given. Results of the experimental studies of the functioning the adaptive antenna array is generalized in regimen of the diagram formation and stochastic inflexion of weighty factor.

Keywords: cosmic devices, measurement of the bearing, antenna array, space-time filter, stochastic inflexion.

 

Введение понятий пространственной частоты и пространственно-временных фильтров радиоволн.

При пространственно-временной обработке сигналов весьма важным параметром является направление прихода сигналов электромагнитного излучения – пеленг q или его угловые составляющие: α – азимут, β – угол места (см. рис. 1). Следуя традиции [1, 2] и близкой аналогии традиционного (временного) спектрального анализа в настоящей работе будем использовать понятие пространственных частот, поскольку они связаны с соответствующими угловыми направлениями. Под пространственной частотой будем понимать скорость изменения фазы в апертуре антенны.

 

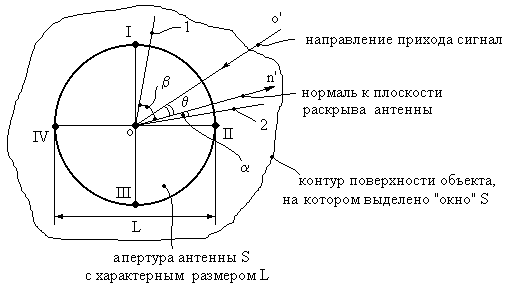
Рис. 1. Угловые соотношения направления прихода сигнала и плоскости апертуры антенны I, II, III, IV, где:

1 – проекция направления oo' на угломестную плоскость I и III;

2 – проекция направления oо' на азимутальную плоскость II и IV.

 

При обычной обработке сигналов с помощью одноканальной схемы независимо от положения точки приема сигналов в пределах выделенной апертуры S на некотором объекте (например, самолете, спутнике) измерить пеленг (моноимпульсно) не представляется возможным.

В случае, если количество точек приема M ³ 3, измерение пеленга может состояться. Для линейного варианта, при М = 2, поскольку пространственная частота

,                                                 (1)

 

где l - длина волны, имеется соответствие между Ω и θ, которое может быть однозначным.

Измерение пеленга может быть обеспечено правильным выбором отношения  и измерением разности фаз Dj прихода сигналов в 1-ю и 2-ю точку приема (см. рис. 2):

                                                   (2)

 

 

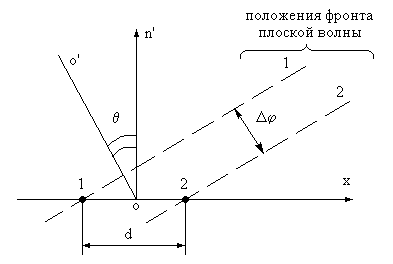
Рис. 2.  Связь разности фаз Dj прихода плоской электромагнитной волны в точки приема 1 и 2 с пеленгом q.

 

Если  - результат измерения, то оценка  пеленга  легко может быть получена из формулы (2):

                                              (3)

 

В случае, если задача измерения пеленга θ основывается на результатах измерения  пространственной частоты Ω, то оценка пеленга

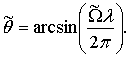                                              (4)

 

При измерении пеленга по пачке  могут быть привлечены ресурсы «удлиняющейся (повторяющейся) серии» измерений. В случае приема сигналов из М точек пространства с помощью плоской фазированной антенной решетки (ФАР) возникает вопрос квантования пространства – «равномерного» размещения точек приема в пределах апертуры S, что эквивалентно выбору требуемого шага квантования d в плоском варианте (см. рис. 3).

 

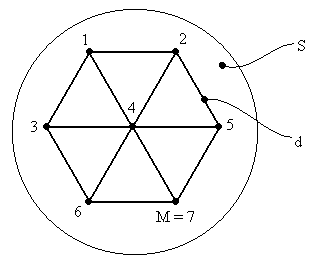
Рис. 3.  Квантование плоского окна апертуры S с помощью семиэлементной (М = 7) пассивной ФАР.

 

В этом случае формула для оценки  пеленга θ по данным измерения  в отличие от (4) учитывает геометрию размещения точек приема, шаг квантования пространства d и является двумерной, т.е. зависит от направления прихода сигнала в азимутальной (α) и угломестной (β) плоскостях. т.к. .

 

Постановка задачи снижения заметности антенных систем в комплексах радиоразведки и радиоэлектронной борьбы космического базирования.

С целью уменьшения заметности космических аппаратов (КА), оснащенных радиотехническими комплексами [3], проведем оценку принципиальной возможности использования стохастических режимов управления параметрами (амплитудно-фазовым распределением поля по раскрыву) адаптивной ФАР.

Отраженный от совокупности N элементарных отражателей участка адаптивного покрытия сигнал  является суперпозицией N пространственных отсчетов (случайного поля) , , взвешенных весовыми коэффициентами (ВК) отражений , определяемых пространственной ориентацией объекта:

Мощность отраженного сигнала, определяющая величину ЭПР, равна

                           (5)

 

где  – оператор математического ожидания.

При фиксированной ориентации объекта, без параметрической накачки ВК  можно считать постоянными, поэтому

                       (6)

 

где элементы пространственной корреляционной матрицы ; поля в раскрыве   мощность входного сигнала.

При определенных фазовых соотношениях весовые коэффициенты a_i увеличивают, либо уменьшают величину P_e.

Ситуация, когда мощность P_e уменьшается, наиболее интересна, так как в этом случае снижается заметность ЛА.

Используя терминологию теории линейных цифровых фильтров (ЦФ) можно сказать, что рассматривая модель рассеивания электромагнитной волны эквивалентна нерекурсивному пространственному ЦФ го порядка с весовыми коэффициентами . В случае, если пространственные ВК ЦФ для некоторой ориентации объекта оказываются согласованными (импульсная пространственная характеристика фильтра и отсчеты  становятся «зеркальными», а их пространственные спектральные характеристики – комплексно-сопряженными), то мы имеем максимум мощности P_e в направлении обратного отражения. Другими словами, возникает эффект «блестящей» точки (направления), при котором отсчеты  когерентно суммируются, приводя к появлению соответствующего пика ЭПР.

В других случаях противоположные знаки коэффициентов , , нарушают условия когерентного суммирования слагаемых, в выражении (5) в результате чего мощность обратного отражения P_e, а следовательно и эффективная поверхность рассеяния (ЭПР) объекта уменьшается. При постоянных весовых коэффициентах  ситуация, связанная с увеличением или уменьшением ЭПР определяется только пространственной ориентацией объекта по отношению к точке наблюдения.

 

Модуляция вектора весовых коэффициентов (критериев).

Рассмотрим подробнее задачу обратную многокритериальной оптимизации [4] амплитудно-фазового распределения поля (функции вектора весовых коэффициентов A(p) = {a₁(p), a₂(p), …, a_N(p)} от заметности p) по раскрыву ФАР. Понятно, что в случае переменных, в частности случайных весовых коэффициентов , открываются дополнительные возможности.

Для пространственного ЦФ со случайными параметрами выражение для мощности  имеет следующий вид:

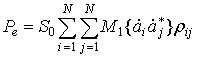,                                (7)

 

где    ;

;

 – средние, среднеквадратические значения и коэффициенты взаимной корреляции весовых коэффициентов  и .

Нормируя (6) к коэффициенту передачи шума 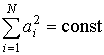 и полагая, что средние значения весовых коэффициентов равны нулю, выражение (7) придем к виду:

,                                                    (8)

 

где .

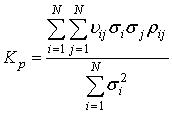Сравнивая (8) с (5) можно сказать, что роль модулей весовых коэффициентов  играют среднеквадратические значения , а роль произведения знаков коэффициентов коэффициенты взаимной корреляции , которые имеют разные знаки и также могут быть знакопеременными, исскуственно, при рандомизации.

Характерной особенностью полученного результата является то, что уровень отраженной мощности  в этом случае уже не зависит от ВК  (пространственной ориентации), а определяется исключительно стохастическими свойствами генератора накачки ВК.

В частности, при независимых ВК, ввиду того, что , для всех , имеем

, ,

то есть пространственный ЦФ становится энергетически «прозрачным», имея равномерную мощностно-угловую характеристику с минимальным уровнем обратного излучения, как в направлении точки наблюдения, так и в других направлениях. Коэффициент усиления мощности  для пространственного ЦФ с неуправляемыми ВК в ситуациях «блестящих» угловых направлений при  равен .

Выигрыш в уменьшении ЭПР приближенно можно оценить величиной

.                                                 (9)

Таким образом, синхронная модуляция (накачка) ВК пространственно-временного фильтра (в данном случае антенной системы) позволяет сохранять основные функции диаграммообразования, но в заданном секторе углов антенная система незаметна.

 

Экспериментальные исследования избирательных свойств пространственных фильтров.

Для проверки теории был задействован макет многолучевой антенной решетки (МЛАР), см. рис. 4, представляющий собой многофокальную линзу с принудительным преломлением.

Излучающая поверхность линзы представляла собой антенную решётку, состоящую из 24-х рупорных антенн, расположенных на полуокружности радиуса 2·R = 480 мм с результирующим шагом 7.5 градусов, поскольку было задействовано 2 уровня, в каждом из которых шаг был равным 15⁰.

 

Рис. 4. Макет многолучевой линзовой антенной решетки:

1 – полуокружность излучающих элементов;

2 – диаграммообразующие устройство (ДОУ).

 

Освещаемой поверхностью линзы являлись антенные элементы в виде открытых концов волновода сечением 28,5 × 12,8 мм, расположенных на окружности радиусом R = 240 мм с шагом 15 градусов. Каждый элемент освещаемой поверхности соединён коаксиальным кабелем с соответствующим элементом излучающей антенной решётки. Важным условием является равенство длин всех кабелей, соединяющих диаграммообразующее устройство (ДОУ) с излучающими элементами. Для задания произвольного амплитудно-фазового распределения возможна замена ДОУ на электрически управляемые фазовращатели. Излучающие элементы в виде открытых концов волноводов аналогичны элементам освещаемой поверхности, расположенной на фокальной дуге, которая является продолжением той же окружности радиусом 240 мм, на которой расположены элементы освещаемой поверхности. Фокальные элементы так- же ориентированы под углом 15 градусов относительно друг друга.

 

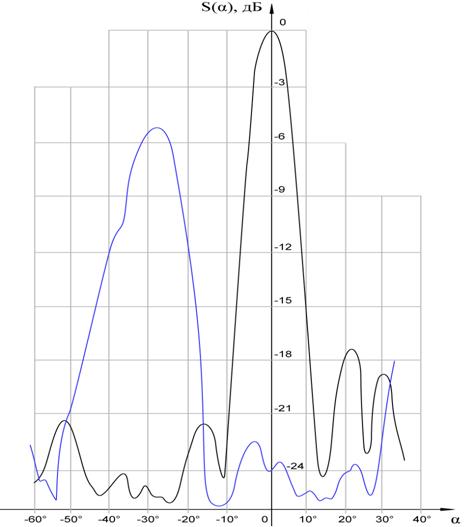
Рис. 5. Диаграмма направленности центрального и крайнего луча в рабочем секторе.

 

Освещаемые и фокальные поверхности объединены в единую конструкцию, которая является диграммообразующим устройством, и  состоящем из 24 элементов, расположенных на окружности R = 240 мм с шагом 15 градусов. Сверху и снизу эти антенные элементы ограниченны металлическими поверхностями, которые формируют двухплоскостную линию передачи между освещаемой и фокальными дугами, расположенных друг напротив друга. Если на некоторый элемент, расположенный на фокальной дуге подаётся СВЧ мощность, то на дуговой излучающей антенной решётке формируется плоский фазовый фронт, поскольку «электрические длины» все выбраны длиной кабелей. Угол наклона фазового фронта к оси симметрии системы, соответствует ориентации «запитывающего» элемента.

 

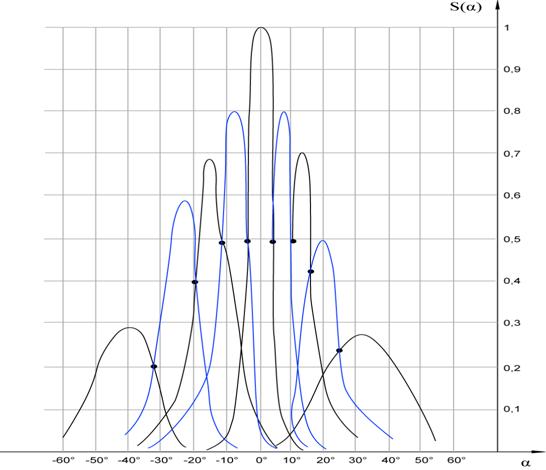
Рис. 6. Уровни пересечения лучей МЛАР при сканировании М = 7.

 

Диаграммы направленности лучей, соответствующих центральному и крайнему лучу рабочего углового сектора МЛАР показаны на рис. 5. Из этого рисунка видно некоторое расширение ширины луча на краю рабочего сектора, отражающим связь пространственной частоты W и пеленга Q и уменьшение усиления из-за конечной ширины (30 градусов) диаграммы направленности отдельного излучающего элемента МЛАР. На рис. 6 показаны уровни пересечения лучей. Измерения проводились на частоте 7.7 ГГц. Как видно из рис 6, уровни пересечения лучей близки к 0.5 (измерения проводились в линейном масштабе). Ширина диаграммы направленности лучей определялась числом излучающих элементов, соединённых с ДОУ. В эксперименте число элементов М было выбрано равным 7, а остальные элементы были нагружены на поглощающие нагрузки. Управление лучами осуществлялось с помощью переключателя и фазовращателей.

При подаче на два смежных фокальных элемента синфазных СВЧ сигналов, то излучающие элементы представляли собой двухэлементную антенную решётку, запитанную синфазно. При подаче - противофазных сигналов, формировалась разностная диаграмма направленности  в соответствующем направлении.

Рисунок 7 иллюстрирует экспериментальные зависимости адаптации АЧХ пространственного фильтра 1-го порядка с окнами  пространственных выборок размером 2, перестраивающихся, соответственно, от ФНЧ (суммарная обработка) к ФВЧ (разностная обработка). Логическая функция перестройки знаков весовых коэффициентов при формировании разностного канала включала в себя две комбинации «+ -» и «- +», то есть соответствовала функции «Å - сумматор по модулю два», а логическая функция перестройки знаков весовых коэффициентов суммарного канала – комбинации «+ +» и «- -», что соответствовала функции эквивалентности.

Стохастический режим абсолютной энергетической прозрачности экспериментально не проверялся, а пролонгировался путем моделирования знакопеременной коммутации знаков весовых коэффициентов с вероятностями p₊ = p_- = 0.5. Данные антенных измерений были взяты из эксперимента. Формирование результирующей характеристики перестраиваемого пространственного фильтра осуществлялось регулировкой корреляции его весовых коэффициентов по аналогии, но с учётом особенностей, определяемых уровнями пересечения ДН рис. 6, в результате которых пространственный фильтр не имел равномерную ДН.

 

Рис. 7. Парциальные и суммарно-разностные диаграммы направленности центрального и смежного с ним луча, задействованной в адаптации произвольных АЧХ пространственных фильтров.

 

Несмотря на это проведенные исследования предопределили теоретическое существование «абсолютно прозрачного фильтра», который бы имел заданную АЧХ, стабильный уровень выходного шума, но к тому же сохранял свойства диаграммообразования, т.е. свойства обеспечения углового разрешения источников электромагнитного излучения. Речь идет о построении ФАР для ЛА нового поколения, который бы был менее заметен из-за антенн, но сам имел возможность получать информацию об окружающей обстановке. Искусственно введённая стохастичность расширила возможности радиолокации.

 Стохастические цифровые фильтры теоретически доказывают такую возможность, однако экспериментальное подтверждение этого эффекта невозможно было обеспечить средствами моделирования, поскольку невозможно учесть большую совокупность неконтролируемых условий и факторов. Вопрос экспериментальной проверки напрашивается сам собой, и его решение, по-видимому, связано с доказательством этой идеи на макете ФАР в ограниченном диапазоне частот и на ограниченном числе пространственных выборок.

 

Обобщения и выводы.

Обобщение результатов экспериментальных исследований и измерений МЛАР позволило установить два режима: работа в режиме диаграммообразования  и работа в режиме стохастической модуляции параметров весовых коэффициентов ФАР для снижения заметности.

На экспериментальной установке МЛАР с многоканальной суммарно-разностной обработкой исследована задача управляемости АЧХ по пространственным частотам Ω для реализации стандартных режимов диаграммообразования, включая режим полной «энергетической прозрачности» в заданном угловом секторе.

Поднятые вопросы, связанные с заметностью КА, имеют много общего с аналогичными вопросами  синтеза ЦФ во временной области и безусловно носят постановочный характер, в дальнейшем они могут стать предметом отдельных исследований.

 

Литература

1.     Горбунов Ю. Н. Цифровые системы СДЦ и их оптимизация: Монография // Государственное образовательное учреждение высшего профессионального образования “Московский государственный институт радиотехники, электроники и автоматики (технический университет)”– М., 2008. – 132 с.

2.     Горбунов Ю. Н. Цифровая обработка радиолокационных сигналов в условиях использования грубого (малоразрядного) квантования: Монография // Федеральное космическое агентство, ФГУП «ЦНИРТИ им. академика А. И. Берга» - М., 2007. –  87 с.

3.     Алексеев А.Г., Штагер Е.А., Козырев С.В. Физические основы технологии STEALTH. – СПб.: ВВМ, 2007 г., 284 с.

4.     Штойер. Р. Многокритериальная оптимизация: теория, вычисления, приложения. М.: Наука, 1982, с. 14-29.