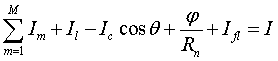УДК 621.3

МОДЕЛИРОВАНИЕ ЭЛЕКТРОМАГНИТНОЙ РЕЗОНАНСНОЙ СИСТЕМЫ С ДЖОЗЕФСОНОВСКИМ ПЕРЕХОДОМ

 

В. В. Павловский

Институт радиотехники и электроники им. В.А. Котельникова РАН

 

Получена 18 марта 2013 г.

 

Аннотация.  В работе представлен метод вычисления статических характеристик джозефсоновского перехода, взаимодействующего с внешней электромагнитной резонансной системой, и компьютерная программа на его основе.  Джозефсоновский переход описывается в рамках резистивной модели, а резонансная система описывается эквивалентной схемой, состоящей из набора произвольного количества RLC контуров. При вычислениях учитываются тепловые флуктуации токов нормальных электронов. Представлены результаты вычисления особенностей вольтамперной характеристики джозефсоновского перехода, связанные с параметрическим резонансом.

Ключевые слова: сверхпроводимость, джозефсоновский переход.

Abstract: A method for calculation of static characteristics of Josephson junction coupled with external electromagnetic resonant system and a computer program based on it are presented. Resistively shunted model is used for description of Josephson junction. Resonant system is presented by an equivalent circuit, which consists of an arbitrary number of RLC circuits. Thermal fluctuations of normal electron currents are taken into account in calculations. Simulation of the junction, which is strongly coupled with a resonator, was performed, and IV-curve features related with parametric resonance were obtained at various temperatures.

Key words: superconductivity, Josephson junction. 

 

Введение

Современный этап развития  электроники терагерцовых частот характеризуется постоянным поиском новых физических механизмов, которые могли бы обеспечить эффективное функционирование элементной базы при частотах свыше 100 ГГц. Одним из таких механизмов является эффект Джозефсона. В настоящее время в  бикристаллических джозефсоновских переходах (ДП), изготовленных из высокотемпературных сверхпроводников (ВТСП), нестационарный эффект Джозефсона наблюдается в частотной области вплоть до 5 ТГц [1]. Это обстоятельство активно используется для развития методов терагерцового спектрального анализа электромагнитного излучения [2] и электромагнитного поглощения в жидкостях [3] . Известно, что статическая нелинейная вольтамперная характеристика ДП (ВАХ) формируется в результате усреднения по времени джозефсоновских колебаний, поэтому  она особо чувствительна к электромагнитному окружению ДП с частотно-зависимыми параметрами. Окружение может включать в себя материал сверхпроводящих контактов ДП и подложки, имеющие частотно-зависимые коэффициенты поглощения электромагнитного излучения, антенну, микрополосковые линии, внешние волноводы и т. д. В частности, этот эффект используется в предложенной в   [4], [5] методике характеризации  электромагнитных структур с помощью джозефсоновской спектроскопии.

Для всех указанных выше приложений требуется использование компьютерного моделирования ДП, взаимодействующего с электромагнитной средой. Эта задача несколько упрощается для бикристаллических ДП из ВТСП на границах зёрен. Вследствие внутреннего шунтирования характеристики этих переходов с высокой точностью описываются резистивной моделью [6]. С другой стороны, необходимость учёта тепловых флуктуаций тока нормальных квазичастиц  приводит к необходимости решать систему стохастических дифференциальных уравнений. В простейшем случае уединённого перехода эта система сводится к уравнению Фоккера-Планка (УФП), для которого существует эффективный алгоритм решения с использованием преобразования Фурье [6]. В более сложных случаях, когда ДП соединён с реактивными элементами, этот метод достаточно сложно применять, так как добавление одного элемента ёмкостного или индуктивного типа увеличивает размерность уравнения Фоккера-Планка. Так в  [7] для анализа ВАХ ДП, шунтированного ёмкостью, использовалось двумерное УФП. Более универсальными являются стохастические методы. В  [8] метод молекулярной динамики использовался для моделирования ДП, соединённого с ёмкостью,  в [9] также анализировалась динамика шунтированного ёмкостью ДП, а тепловые флуктуации моделировались в виде последовательности прямоугольных импульсов со случайной амплитудой.

В настоящей работе представлена компьютерная программа, реализующая алгоритм на основе решения стохастических дифференциальных уравнений (СДЕ) с использованием формулы Ито [11]. Программа предназначена для моделирования ДП, который взаимодействует с резонансной электромагнитной системой. Резонансная система представлена в виде эквивалентной схемы из произвольного количества RLC цепочек и имеет частотную зависимость импеданса достаточно общего вида. Указанный алгоритм позволяет эффективно реализовать параллельный вычислительный процесс в многопроцессорной системе.  В [10] с использованием этого алгоритма моделировалась более простая система, в которой к ДП были параллельно присоединены ёмкость и RL-цепочка.

1. Основные уравнения и алгоритм решения

На рис. 1. представлена эквивалентная схема резонансной системы с ДП. R_kL_kC_k-цепочки представляют отдельные резонаторы, которые могут моделировать излучающие элементы широкополосной антенны, отдельные участки амплитудно-частотной характеристики микрополосковой структуры или резонансное поглощение в материале ДП или подложки, связанное, например, с возбуждением оптических фононов.  R_CC – цепочка моделирует элементы с широкополосным поглощением электромагнитного излучения, такие как длинная микрополсковая линия и выделена в отдельный контур для большей эффективности вычислений.

 

 

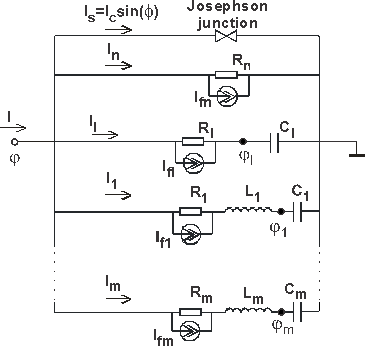
Рис. 1. Эквивалентная схема резонансной системы с ДП.

 

Используя резистивную модель ДП, можно записать следующие уравнения:

,

 

,

 

,

                                       ,                         (1)

,

 

,

 

где M – число RLC контуров, m=1,…,M, q=f+p/2, f - джзефсоновская разность фаз,   d(t) – функция Дирака, k – постоянная Больцмана, I_c – критический ток, h- постоянная Планка, R_n –сопротивление ДП в нормальном состоянии, T – температура, e – заряд электрона, M – число RLC контуров, m=1,…,M.. Тепловые флуктуации тока представлены в виде гауссова случайного процесса:

                               ,  .

Для получения статической ВАХ необходимо усреднить полученное решение на достаточно большом отрезке времени. Используя (1) для напряжения смещения V получим следующее выражение:

                                   при .                                (2)

 

В дальнейшем будем использовать (1) в безразмерном виде, нормируя все токи на I_c, потенциалы – на V_c, время – на , индуктивность – на , ёмкость – на   , где V_c=I_cR_n – характеристическое напряжение ДП, .

В безразмерном виде после преобразований (1) можно записать в стандартном для СДЕ виде:

dX=a(t,X)dt+sdW                                                      (3)

где X и a - векторы со следующими компонентами: X₁= q, X₂=j_c, X_2+m=I_m, X_2+M+m=j_m, m=1,…M.

,,   , ,
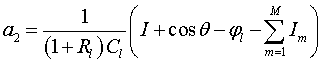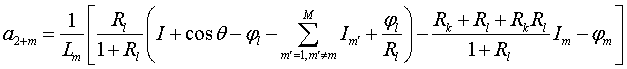W-вектор, у которого отличны от 0 компоненты W₁, W₂ и W_2+m, которые являются винеровскими случайными процессами: ,  где  – случайная переменная, удовлетворяющая условию: .

 s  представляет собой матрицу со следующими компонентами:

 , , , ,

,   ,  .

 

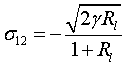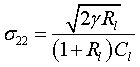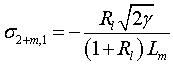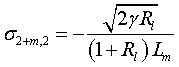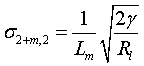Остальные компоненты матрицы s  равны 0.

Для получения численного решения (3) используем полунеявную одношаговую разностную схему порядка Dt^3/2  [11], в которой нелинейные члены с sinq и cosq представлены в явном виде. Полученная при этом система линейных конечно-разностных уравнений решается методом LU-разложения.  Для получения зависимости V(I),  наряду с усреднением по времени, можно использовать усреднение по реализациям решения. Это позволяет эффективно использовать параллельные вычисления.

Решение (3) осуществляется в компьютерной программе, которая вычисляет ВАХ и зависимость дифференциального сопротивления от напряжения R_d(V) ДП. Программа реализована для операционной системы Linux с использованием библиотеки потоков (libpthread). В качестве генератора случайных чисел используется векторный генератор случайных чисел с гауссовым распределением на основе алгоритма ICDF из библиотеки Intel Math Kernel  Library  [12].

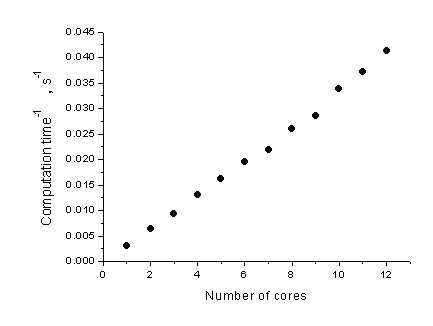
Для проверки масштабируемости были проведены  вычисления на системе с двумя 6-ядерными процессорами Intel Xeon 2.4 ГГц. Тестовая структура содержала один колебательный контур, усреднение производилось по 128 реализациям решения и каждая реализация содержала 10⁶ точек времени. Для выполнения программы требовалось 3.6 Гб оперативной памяти. Зависимость обратного времени вычислений от количества ядер, представленная на рис.2, демонстрирует линейную масштабируемость.

 

 

Рис. 2 Зависимость обратного времени счёта программы от количества используемых вычислительных ядер.

 

На рис. 3 приведены результаты вычислений R_d(V) для ДП без резонансной системы, выполненных с помощью решения уравнения Фоккера-Планка [6] решения стохастических уравнений, выполненного с помощью разработанной программы. Вычисления проводились для типичных значений параметров бикристаллических ДП из YBa₂Cu₃O_7-x: I_c=0.5 мА, R_n=2 Ом, T=40 К.

 

 

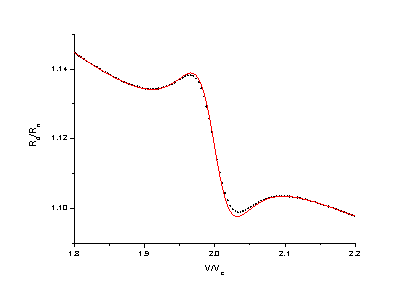
Рис. 3 Результаты вычисления зависимости дифференциального сопротивления джозефсоновского уединённого перехода от напряжения. Сплошная линия – решение уравнения Фоккера-Планка, пунктирная линия – из решения системы стохастических уравнений.

 

На рис. 4 представлено сравнение результатов численного расчёта R_d(V) для ДП, взаимодействующего с одним колебательным контуром с результатами вычислений по аналитической формуле, полученной в соответствии с [13]:

 ,                  (4)

 

где dR_d(I) - изменения дифференциального сопротивления  R_d(I), связанное с влиянием внешней системы с адмиттансом Y(f), взаимодействующей с ДП, f – частота, связанная с напряжением смещения соотношением Джозефсона: V = hf/2e. Выражение (4) применимо в случае dR_d(I) << R_d(I) и T=0, в соответствии с чем подобраны параметры системы R₁/R_n=200, 2pf₀/W_c=2, Q=20, где  - резонансная частота и 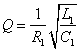 - добротность колебательного контура.

 

 

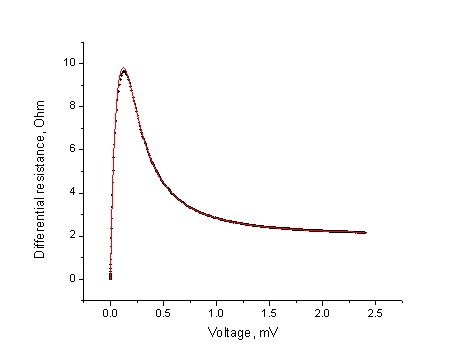
Рис. 4.  Результаты вычисления зависимости дифференциального сопротивле­ния джозефсоновского уединённого перехода от напряжения. Сплошная линия – вычисление по формуле (4), пунктирная линия – из решения системы стохастических уравнений.

2. Параметрический резонанс в системе из джозефсоновского перехода и резонансной структуры

В качестве примера применения разработанной компьютерной программы рассмотрим моделирование параметрического резонанса в системе ДП и связанного с ним резонатора. Решение этой задачи приведено в [6] в приближениях слабой связи резонатора с ДП и малых флуктуаций.  Рассмотрим ДП, который соединён с колебательным контуром с резонансной частотой f₀. При увеличении тока, когда напряжение смещения на ДП достигает некоторой величины в окрестности значения V₀=hf₀/2e, происходит возбуждение системы на резонансной частоте колебательного контура и напряжение на ДП скачком достигает значения V₀. Этот эффект имеет место при достаточно хорошем согласовании ДП с резонатором (R₁~R_n) и высокой добротности резонатора.  На рис. 5 приведены результаты вычисления ВАХ ДП для такого случая в отсутствие флуктуаций (T=0). Были выбраны следующие значения параметров: I_c=0.5 мА, R_n=2 Ом, f₀=300 ГГц, Q=100, R₁=2 Ом.  Частоте резонатора соответствует напряжение V₀=0.62 мВ.  Отметим особенности при напряжениях V₀/2, V₀/3, V₀/4, …. Эти особенности связаны с тем, что в спектре генерации ДП кроме основной присутствуют кратные гармоники.

Вблизи напряжения V₀ наблюдается гистерезисное поведение, которому должен соответствовать участок с отрицательными значениями R_d при V₁<V<V₀.(на рис. 2 этот участок ВАХ показан штриховой линией). Такие участки обычно могут быть рассчитаны (и измерены) с помощью включения элемента в цепь с нагрузочным резистором. В случае ДП из-за динамической природы ВАХ требуется разработка более сложной схемы и расчет этого участка в данной статье не рассматривается.  

 

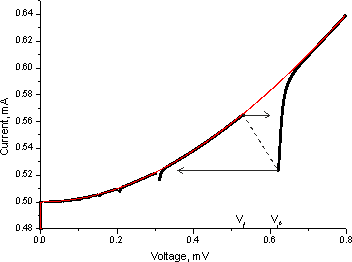
Рис. 5.  Результаты вычисления вольтамперной характеристики джозефсоновского перехода, от напряжения при T=0.
Сплошная линия – уединённый переход, пунктирная линия – переход связан с резонатором.

 

 

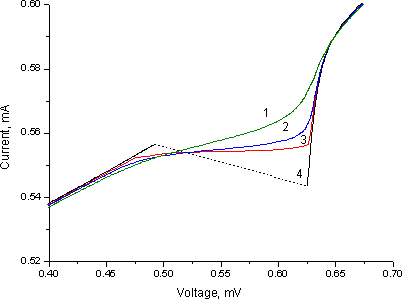
Рис. 6.  Результаты вычисления вольтамперной характеристики джозефсоновского перехода, от напряжения при различных температурах T.
1 – T=60 К, 2 –T=30 K, 3 – Т=20 К, 4 – T=4  К.

На рис. 6 приведены зависимости ВАХ ДП при различной интенсивности тепловых флуктуаций, задаваемых вариацией температурой. Предполагается, что температура ДП равна температуре резонатора. Такой эксперимент можно поставить, используя ДП с достаточно большим значением I_c и помещая его в магнитное поле так, чтобы уменьшая поле компенсировать изменение  I_c с ростом температуры. С ростом интенсивности флуктуаций при 20 К параметрическое возбуждение исчезает и на ВАХ  (и R_d(V)) остаётся особенность, связанная с резонансом внешней электродинамической системы, которая сглаживается при дальнейшем увеличении T.

Полученные результаты качественно совпадают с результатами приближённого расчёта в рамках резистивной модели, представленными в [6].

Заключение

Представлен метод моделирования ДП, взаимодействующего с внешними электромагнитным окружением, включающим в себя резонансные структуры, в условиях тепловых флуктуаций токов нормальных электронов.  Рассматриваются структуры, электромагнитные характеристики которых могут быть описаны в рамках эквивалентных схем, включающих в себя произвольное число последовательных RLC контуров. Метод основан на решении системы стохастических уравнений резистивной модели ДП и реализован в виде компьютерной программы, использующей многопоточные вычисления. Для  тестовых задач, допускающих использование аналитических выражений и численного решения уравнения Фоккера-Планка, получено близкое совпадение результатов расчетов разработанным и альтернативными методами. В качестве примера применения метода представлены результаты моделирования влияния тепловых флуктуаций на параметрическое возбуждение ДП в резонаторе. Разработанный метод и программа на его основе могут быть использованы для оптимизации согласования ДП с антеннами и микрополосковыми линиями в детекторах электромагнитного излучения, а также для анализа данных характеризации электромагнитных структур с помощью джозефсоновской спектроскопии.

  Настоящая работа поддерживается РФФИ (гранты №11-07-00544-а, 11-07-12023-офи-м и 11-02-91321-сиг_а) и Министерством образования и науки РФ (контракт №11.519.11.4005). Авторы признательны Intel Corporation за возможность использования программного обеспечения Intel Math Kernel Library.

 

Литература

1. Дивин Ю.Я., Котелянский И.М., Губанков В.Н. Бикристаллические джозефсоновские переходы из с-ориентированных YBa₂Cu₃O_7-x пленок для терагерцовой Гильберт-спектроскопии. РЭ, 2003, Т. 48, № 10, С. 1238-1249.

2. Дивин Ю.Я., Попе У., Котелянский И.М., Губанков В.Н., Урбан К.. Терагерцовая спектроскопия на основе джозефсоновских переходов из высокотемпературных сверхпроводников. // РЭ, 2008, T.53, C.1205-1222.

3. Lyatti M., Divin Y., Poppe U., Urban K. Liquid identification by Hilbert spectroscopy // Supercond. Sci. Technol., 2009 V. 22, N. 11, P. 114005.

4. Волков О.Ю., Губанков В.Н., Гундарева И.И, Дивин Ю.Я., Павловский В.В. Джозефсоновская адмиттансная спектроскопия характеристик логопериодической антенны в субмиллиметровом диапазоне длин волн. РЭ, 2009, т.  54, № 11, с. 1381–1386.

5. Volkov O.Y., Divin Y.Y., Gubankov V.N., et. al. Terahertz characterization of external resonant systems by high-T_c Josephson junctions. // IEEE Transactions on Applied Superconductivity, 2011, V. 21, N. 3, P. 306-310.

6. Лихарев, К.К.. Введение в динамику джозефсоновских переходов. М., Наука, 1985, 320 С.

7. Yoshida K. Effect of capacitance on noise-rounded current-voltage curves of a Josephson tunnel junction. // J. Appl. Phys., 1982, V.53, N.11, P. 7471-7478.

8. Kurkijarvi J., Ambegaokar V. Numerical calculation of thermal noise-voltage in a Josephson junction of finite capacitance // Phys. Lett. , 1970,   V. 31A, N. 6, P. 314-315.

9. Busse F., Nebel F.L., Herzog P.  Effect of noise and capacitance on the dynamical characteristics of high-T, Josephson junctions. // Appl. Phys. Lett., 1993, V. 63,  N. 12, P. 1687-1868.

10. Whan C. B., Lobb C. J.,  Forrester M. G. Effect of inductance in externally shunted Josephson tunnel junctions. // J. Appl. Phys., 1995, V.77, N.1, P. 382-289.

11. Milstein G. N., Tretyakov M. V. Stochastic Numerics for Mathematical Physics. Berlin, Springer, 2003, 594 P.

12. Intel Math Kernel Library // [Электронный ресурс]. URL: http://software.intel. com/en-us/intel-mkl

13. Волков А.Ф. Влияние импеданса внешней цепи на вольтамперную характеристику джозефсоновского перехода. Радиотехника и электроника. // 1972, Т.17, С.2581-2583.