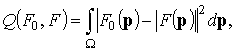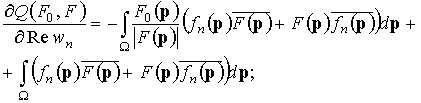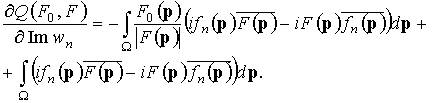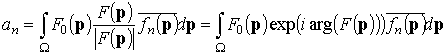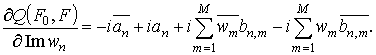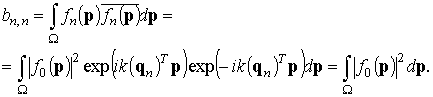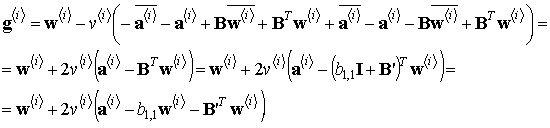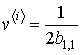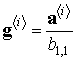УДК 621.396.677
БЫСТРОДЕЙСТВУЮЩИЙ МЕТОД СИНТЕЗА МНОГОЭЛЕМЕНТНЫХ АНТЕННЫХ РЕШЕТОК С УПРОЩЕННОЙ ГРАДИЕНТНОЙ
ПРОЦЕДУРОЙ
С. Е. Мищенко, С. А. Шелкоплясов
Научно-исследовательский институт физики Южного федерального университета
Статья получена 28 октября 2013, после доработки – 10 марта 2014 г.
Аннотация. Обоснован новый итерационный метод синтеза многоэлементных антенных решеток по требованиям к заданной амплитудной диаграмме направленности. Предлагаемый метод за счет упрощения итерационной процедуры обеспечивает существенный выигрыш по сравнению с классическими градиентными методами синтеза, что показано в ходе сопоставления предлагаемого и существующего методов.
Ключевые слова: антенная решетка, диаграмма направленности, амплитудно-фазовый синтез, фазовый синтез.
Abstract. The new iterative method of antenna array synthesis according to requirements to the amplitude preassigned radiation pattern is substantiated. The offered method due to simplification of iterative procedure provides a considerable gain in comparison with classical gradient methods of synthesis, what is shown during comparison of offered and existing methods.
Keywords: antenna array, radiation pattern, amplitude-phase synthesis, phase synthesis, gradient.
Введение
Тенденцией развития современных радиосистем является использование многоэлементных антенных решеток (АР), применение которых обеспечивает многофункциональность системы за счет расширения класса формируемых диаграмм направленности (ДН). При этом на этапе проектирования АР необходимо обоснование характеристик антенны в ходе решения задач амплитудно-фазового и фазового синтеза по требованиям к объемным амплитудным диаграммам направленности (ДН). Реализация большинства известных методов аппроксимационного синтеза для решения подобных задач показывает существенные ограничения с точки зрения разрешения противоречия между размерностью задачи и качеством ее решения. В связи с этим представляет интерес разработка новых методов синтеза АР, ориентированных на решение задач большой размерности.
Цель статьи состоит в разработке быстродействующего итерационного метода синтеза многоэлементной АР и сопоставлении его с обычными итерационными методами.
В основу предлагаемого метода лег алгоритм, предложенный в работе [1]. В данной работе для решения задач фазового синтеза по требованиям к амплитудной объемной ДН предлагалось на каждом итерационном шаге использовать преобразование Фурье ДН, формируемой при заданном или текущем амплитудно-фазовом распределении. По сути данный алгоритм состоит в том, что:
− для заданного начального амплитудно-фазового распределения (АФР) формируется комплексная ДН АР;
− формируется комплексная заданная ДН путем перемножения заданной амплитудной ДН и фазовой части сформированной комплексной ДН АР;
− выполняется Фурье-перобразование комплексной заданной ДН. Полученные комплексные коэффициенты Фурье считаются новым АФР;
− с новым АФР выполняется формирование комплексной ДН АР и проверяется ее соответствие заданным требованиям. В случае соответствия решение задачи останавливается, в противном случае осуществляется переход ко второму шагу.
Реализация алгоритма показала его высокую численную эффективность, однако в работе [1] отсутствовало математическое обоснование подхода.
1. Постановка задачи
Рассмотрим 
-элементную АР с излучателями, комплексные
ДН которых описываются функциями 
и образуют
вектор-столбец 
, где 
−
единичный вектор, указывающий на точку наблюдения. Пусть амплитудно-фазовое
распределение описывает комплексный вектор 
.
Тогда формируемая ДН АР может быть записана в виде:
,
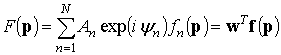(1)
где символ «Т» обозначает операцию транспонирования.
Предположим, что форма
заданной ДН определена с помощью действительной неотрицательной функции 
.
Это позволяет
сформулировать задачу о приближении заданной и синтезированной ДН в виде
оптимизационной задачи, состоящей в отыскании амплитуд 
и
фаз излучателей 
, обеспечивающих минимизацию диаграммного
функционала:
Производная данного функционала является функцией с разрывом в окрестности экстремума. Покажем это на примере простейшей двухэлементной антенны, ДН которой описывается выражением вида:
,
(3)
где 
−
комплексная амплитуда возбуждения 
-го элемента 
; 
−
расстояние между элементами; 
; 
.
Найдем приращение функционала (2) по разностной схеме:
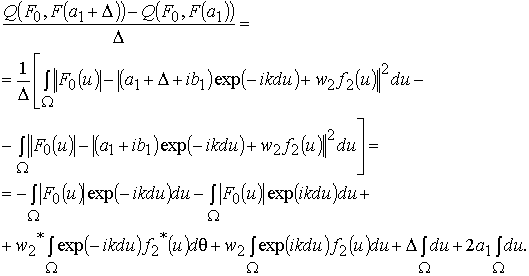(4)
Аналогично найдем:
(5)
В выражениях (4) и (5) символ «*» обозначает операцию комплексного сопряжения.
В точке экстремума функционала
(2) производные (4) и (5) должны принимать нулевое значение, т.е. сумма всех
слагаемых в (4) и (5) должна быть равна нулю. Однако при малых приращениях 
слагаемое 
меняет
свой знак в зависимости от знака 
. Вне точки экстремума
данное слагаемое не вносит достаточный вклад для того, чтобы повлиять на знак
производной. Это означает, что применение градиентного подхода для нахождения
минимума функционала (2) является корректным до тех пор, пока решение не
попадет в точку минимума. В этом случае вектор градиента будет ориентироваться
в направлении, зависящем от знака приращения. Полученные выражения могут быть
обобщены на случай АР с произвольным числом элементов. При этом 
представляет собой ДН АР без одного
элемента, по комплексной амплитуде которого ведется дифференцирование.
Неопределенность знака производной в сколь угодно малой окрестности точки минимума функционала (2) указывает на наличие разрыва и его негладкость. В связи с этим в известной литературе такой функционал применяется редко или приводится к виду, который используется, например, в [2] и учитывает реактивную мощность антенны. Однако в данном случае применение функционала задачи в виде (2) является принципиальным.
Если ограничения на
амплитуды отсутствуют, то сформулированная задача
относится к классу задач амплитудно-фазового синтеза АР.
При
наличии дополнительных ограничений на амплитудное распределение задача
переходит в разряд задач фазового синтеза и неизвестными являются только фазы .
2. Метод решения задачи
Будем решать сформулированную задачу градиентным методом.
Следует отметить, что при решении задач амплитудно-фазового и фазового аппроксимационного синтеза градиентными методами итерационные процедуры отличаются несущественно, что позволяет вести изложение сути предлагаемого метода применительно к задачам как амплитудно-фазового, так и фазового синтеза.
Пусть на входе в
итерационную процедуру синтеза известно начальное амплитудно-фазовое
распределение 
. Здесь 
обозначает
номер шага итерационного процесса. Тогда новое амплитудно-фазовое распределение
находят при движении в сторону
антиградиента диаграммного функционала вида (2):
где 
−
шаг приближения к экстремуму.
При наличии ограничений на форму амплитудного распределения, т.е. при решении задач фазового синтеза вводится дополнительная операция [3]:
При решении задач амплитудно-фазового синтеза вместо (7) используют комплексные амплитуды
На каждом шаге итерационного
процесса вычисляется значение диаграммного функционала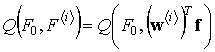 
и
выполняется его сравнение с полученным на предыдущем шаге с помощью неравенства:
Если неравенство (9)
нарушается, то 
.
При использовании (6)
начальное значение параметра 
выбирается произвольно.
Для заданного диаграммного функционала (2) частные производные в выражении (9) могут быть представлены в виде:
В выражениях (10), (11) и в дальнейшем черта над функцией обозначает операцию комплексного сопряжения.
Анализ выражений (10) и (11) показывает, что они могут быть представлены в виде суперпозиции интегральных коэффициентов двух видов:
С учетом обозначений (12) и (13) выражения (10) и (11) примут следующий вид:
Как правило, функцию 
представляют в виде произведения амплитудной
ДН излучателя 
и экспоненциального множителя 
, в котором 
−
волновое число; 
− вектор, указывающий на
фазовый центр -го излучателя АР.
Это означает, что при
совпадении индексов и 
получим:
Отсюда следует, что
диагональные элементы матрицы 
являются одинаковыми и чисто действительными.
Для произвольных индексов
и запишем:
Анализ выражений (16) и
(17) показывает, что матрица 
является эрмитовой.
Представим матрицу в виде суммы единичной матрицы 
и матрицы внедиагональных элементов
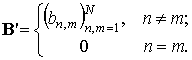(18)
Тогда выражение (6) можно записать в векторном виде:
Если значение скорости
приближения к экстремуму связать со значением диагонального элемента матрицы , т.е. положить
то выражение (19), определяющее рассматриваемую итерационную процедуру синтеза АР, упростится к виду:
Выражение (21)
представляет собой упрощение классической градиентной итерационной процедуры
синтеза, так как из процедуры (21) по сравнению с (6) исключен параметр . Это позволяет в ходе синтеза отказаться
от проверки качества формирования ДН. И ограничить длительность процесса решения
максимальным числом итераций.
Дополнительное упрощение
может быть получено, если считать, что амматрица является
диагональной и амплитуды диагональных элементов равны. Это условие будет
выполняться в том случае, когда ДН излучателей описываются ортогональными функциями.
Данное условие, например, точно выполняется для линейки изотропных точечных
излучателей размещенных с шагом 
, и приближенно
выполняется для многих линейных и плоских раскрывов. Диагональные коэффициенты
матрицы равны друг другу, если решетка состоит из
идентичных излучателей. При выполнении данных условий 
.
Подставляя данное соотношение в (19) с учетом (20), получим:
Таким образом, полученные аналитические соотношения, определяющие итерационную процедуру синтеза АР в смысле оптимизации диаграммного функционала (2) позволили предложить следующий метод решения задачи.
Сначала при построении
математической модели АР оцениваются элементы матрицы .
Из сравнения амплитуд диагональных и внедиагональных элементов принимается
решение об использовании итерационной процедуры (21) или (22).
После задания формы заданной амплитудной ДН и начального амплитудно-фазового распределения осуществляется операция формирования текущей ДН. Сформированная текущая ДН АР и заданная амплитудная ДН используются для расчета интегральных коэффициентов с использованием выражения (12).
После этого с помощью
выражений (21) или (22) находятся комплексные амплитуды 
.
В зависимости от наличия или отсутствия ограничений на форму амплитудного распределения выполняются операции (7) или (8), которые приводят к новому амплитудно-фазовому распределению.
Выход из итерационного процесса может быть осуществлен либо по окончании заданного интервала времени или выполнения числа шагов итерационного процесса, либо на основании сопоставления качества формируемой ДН с заданной.
3. Численные результаты
В качестве примера рассмотрим
решение задачи синтеза безлепестковой ДН с шириной луча 5,7º в главных плоскостях
с помощью АР из 1264 элементов. Излучатели АР размещены в узлах прямоугольной
сетки с шагом 
. Амплитудная ДН излучателей
описывались функцией 
. Геометрия задачи приведена на
рис. 1.
Рис. 1. Геометрия исследуемой антенной решетки
В ходе исследований
необходимо было найти амплитудно-фазовое распределение ,
обеспечивающее минимум диаграммного функционала (2). При этом при решении
задачи амплитудно-фазового синтеза ограничения на форму амплитудного
распределения не накладывались. При решении задачи фазового синтеза форма
амплитудного распределения задавалась формулой:
. (23)
На первом этапе численных исследований рассматриваемые итерационные процедуры синтеза были программно реализованы таким образом, чтобы была возможность сопоставления скорости полученных алгоритмов при заданном числе итераций, которое было выбрано равным 200. Это позволило оценить временные затраты на реализацию каждого из методов.
На втором этапе в итерационные процедуры были включены операции оценки качества приближения синтезированной ДН к заданной с помощью диаграммного функционала (2). Полученные результаты с помощью оценок быстродействия первого этапа были размещены на временной шкале.
На рис. 2 приведены зависимости сходимости итерационных процессов амплитудно-фазового синтеза при одинаковых начальных параметрах в течение 200 итераций.
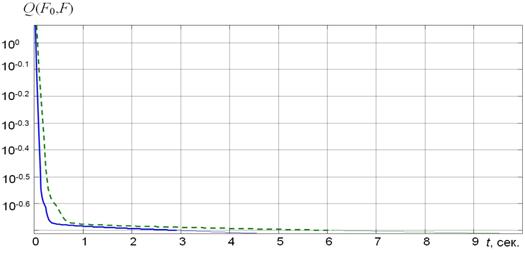
Рис. 2. Сходимость методов при решении задачи амплитудно-фазового синтеза АР
Сплошная кривая отражает сходимость решения задачи амплитудно-фазового синтеза АР с помощью метода, использующего итерационную процедуру вида (22), обеспечивающую наиболее высокую скорость решения задачи. Пунктирная кривая иллюстрирует сходимость решения задачи синтеза при использовании общей градиентной итерационной процедуры вида (6) и упрощенной процедуры, описываемой выражением (21). Сходимости двух последних алгоритмов совпадают с графической точностью, что объясняется выбором одинаковой начальной скорости приближения к экстремуму (20) и отсутствием необходимости дробления данного параметра в ходе решения задачи амплитудно-фазового синтеза.
На рис. 3 представлены сечения синтезированных ДН в вертикальной плоскости.
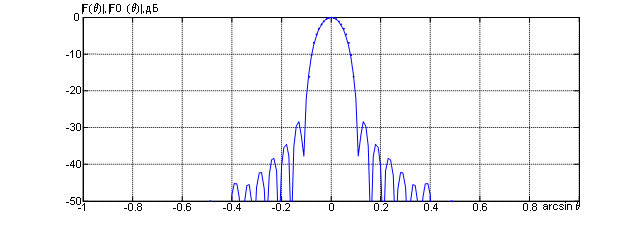
Рис. 3. Синтезированные и заданная ДН задачи амплитудно-фазового синтеза АР
На данном рисунке точками показана заданная ДН, синтезированные ДН совпали с графической точностью при использовании всех трех итерационных процедур.
Анализ полученных результатов при решении задачи амплитудно-фазового синтеза показал, что с точки зрения качества решения все три итерационные процедуры идентичны. Однако использование предлагаемого метода синтеза позволяет повысить быстродействие более чем в два раза (с 9,5 до 4,5 секунд). Это достигается за счет того, что отсутствие необходимости дробления шага позволяет избежать трудоемких в вычислительном отношении оценок качества синтезированной ДН на каждой итерации. В то же время отсутствие параметров задачи, позволяющих оценить текущее качество решения не позволяет установить точное время выхода из итерационного процесса. Это ограничение предлагаемого метода является незначительным, если процедура синтеза в процессе проектирования антенны повторяется многократно.
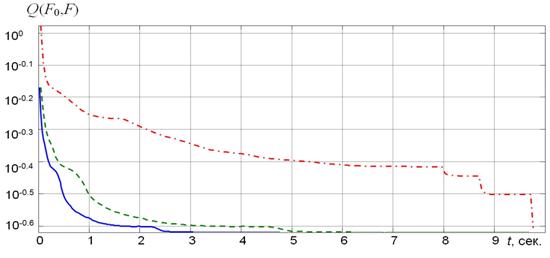
На рис. 4 представлены зависимости сходимости методов фазового синтеза.
Рис. 4. Сходимость методов при решении задачи фазового синтеза АР
Сплошная и пунктирные кривые соответствуют решению задачи с использованием итерационных процедур (22) и (21) соответственно. Штрихпунктирная кривая показывает сходимость градиентной процедуры вида (6).
Первые две кривые в конечном итоге привели к одинаковому качеству решения. В результате синтезированные ДН совпали с графической точностью (сплошная кривая на рис. 5).
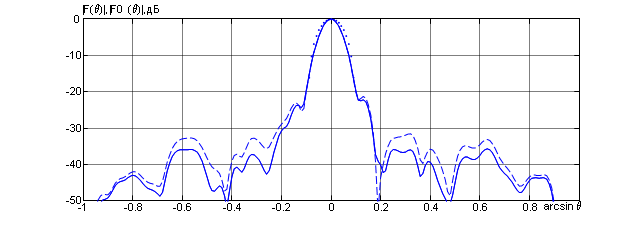
Рис. 5. синтезированные и заданная ДН задачи фазового синтеза АР
Существенный проигрыш в
быстродействии показал классический подход к минимизации диаграммного
функционала (2) (штрихпунктирная кривая на рис. 4). Это обусловлено не только
необходимостью оценки качества решения на каждой итерации, но и выбором
начального значения параметра .
В результате решения задачи после 200 итераций классический метод не позволил добиться качества решения, к которому привели упрощенные процедуры фазового синтеза. Пунктирная кривая на рис. 5 показывает сечение сформированной объемной ДН с помощью градиентной процедуры (6) после 200 итераций.
В целом сопоставление предлагаемого и известного методов решения задач фазового синтеза показало, что предлагаемый быстродействующий метод синтеза, основанный на выражении (22), обеспечивает четырехкратное преимущество по скорости решения задачи перед известным методом проектируемого градиента (выражение (6)) и двукратное − перед процедурой синтеза (21). Это позволяет заключить, что предлагаемый метод синтеза при неизвестном достаточном числе итераций может быть использован в качестве грубого приближения синтезированной ДН к заданной. После выполнения определения числа шагов с помощью сокращенной процедуры синтеза (22) может использоваться классический метод градиентного синтеза.
Заключение
Таким образом, проведенные исследования показали, что предлагаемый итерационный метод синтеза АР по заданной амплитудной ДН существенно превосходит по быстродействию классический градиентный метод синтеза АР [3]. Повышение вычислительной эффективности по сравнению с известным методом достигается за счет упрощения выражения для градиента диаграммного функционала и исключения той части операций, которая связана с оценкой качества решения на текущем шаге. Это позволило при решении задач амплитудного синтеза увеличить быстродействие метода более чем в 2 раза при сохранении качества решения, а при решении задач фазового синтеза добиться 4-х кратного увеличения скорости при незначительных отличиях в качестве решения задачи синтеза. Следует отметить, что по мере увеличения числа излучателей в составе АР выигрыш в быстродействии будет только увеличиваться. Это позволяет утверждать, что предлагаемый метод синтеза целесообразно использовать при решении задач амплитудно-фазового и фазового синтеза многоэлементных АР.
1 Грибанов А.Н. Фазовый синтез лучей специальной формы в фазированных антенных решетках бортовых РЛС // Диссертация кандидата технических наук. − М.: Изд.во МГИРЭА, 2007, 206с.
2 Зелкин Е.Г., Кравченко В.Ф., Гусевский В.И. Конструктивные методы аппроксимации в теории антенн. − М.: САЙНС-ПРЕСС, 2005, 512с.
3 Зелкин Е.Г., Соколов В.Г. Методы синтеза антенн: Фазированные антенные решетки и антенны с непрерывным раскрывом. - М.: Сов. радио, 1980. − 296с.