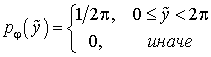Имитационная компьютерная модель гиромагнитного материала на основе частиц гексаферрита

ИМИТАЦИОННАЯ КОМПЬЮТЕРНАЯ МОДЕЛЬ ГИРОМАГНИТНОГО МАТЕРИАЛА НА ОСНОВЕ ЧАСТИЦ ГЕКСАФЕРРИТА

П. С. Колодин, Б. П. Поллак, А. В. Раков
Национальный исследовательский университет «МЭИ»

Статья получена 12 марта 2014 г.

Аннотация. Завершается начатая в [1] работа по развитию существующей математической модели гиромагнитного материала на основе частиц гексаферрита. Описаны основные идеи и принципы имитационного компьютерного моделирования, позволяющие обобщить существующую модель на случай произвольных значений параметров, описывающих качество текстуры и пространственную ориентацию материала, а также значение внешнего магнитного поля. Эти идеи реализованы в обобщенной компьютерной модели гиромагнитного материала на основе частиц гексаферрита. С помощью разработанной компьютерной модели проведен расчет резонансных кривых при варьировании указанных параметров.

Ключевые слова: гиромагнитный материал, гексаферрит, имитационное компьютерное моделирование.

Abstract. The existing mathematical model for gyromagnetic material based on hexaferrite particles has been improved. Main ideas and principles of computer imitation modeling as an improvement basis are described; they allow modeling with arbitrary values of material texture quality and spatial orientation and applied magnetic field density. These ideas and principles have been implemented in improved model for gyromagnetic material based on hexaferrite particles. Resonance curves with variation of specified values are calculated upon the basis of improved model.

Keywords: gyromagnetic material, hexaferrite, computer imitation modeling.

Введение

Одной из актуальных задач современной радиоэлектроники является освоение (в частности, с целью создания сверхскоростных коммуникационных линий [2]) коротковолновой части диапазона крайне высоких частот (КВЧ). Решение этой задачи включает в себя разработку различных функциональных устройств.

Как известно, этапам изготовления макета радиотехнического устройства и его испытаний на практике предшествует процесс проектирования, который для устройств диапазона КВЧ в настоящее время практически не обходится без компьютерного моделирования электродинамических процессов.

К настоящему времени при создании различных устройств КВЧ (например, резонансных вентилей, полосовых фильтров и др.) широкое распространение получили гексаферритовые гиромагнитные резонаторы [3] – образцы материалов на основе частиц гексаферрита[1], работающие в условиях ферромагнитного резонанса (ФМР). Для возможности моделирования электродинамических процессов и компьютерного проектирования таких устройств необходима компьютерная модель гексаферритового гиромагнитного резонатора, для создания которой, в свою очередь, необходима компьютерная модель гиромагнитного материала на основе частиц гексаферрита.

Ранее сотрудниками отраслевой проблемной лаборатории ферритов МЭИ на основе известных теоретических представлений и имеющихся экспериментальных фактов была разработана приближенная теория ФМР в материалах на основе частиц гексаферрита и создана математическая модель для расчета одного из основных электродинамических параметров материала – тензора магнитной восприимчивости [4]. И хотя теория позволяла качественно объяснять и предсказывать результаты различных экспериментов, количественное сопоставление эксперимента и математической модели было затруднительно. Математическая модель, записанная в общем виде, была слишком громоздка и неудобна для проведения вычислений, а получение простых аналитических выражений было возможно только при использовании ряда приближений и допущений. Разумеется, их использование не могло не сказаться на области применимости результата, поэтому приближенная математическая модель, полученная позже в результате такого упрощенного анализа [5], могла быть обоснованно применена только для материала, намагниченного до насыщения и ориентированного осью текстуры параллельно вектору напряженности внешнего поля.

Первая попытка использования этой теории для создания компьютерной модели гиромагнитного материала на основе частиц гексаферрита заключалась в компьютерной реализации приближенной математической модели [6]. Однако компьютерная модель, полученная таким способом, содержала в себе тот же самый набор математических приближений, что и математическая модель из [5], поэтому ее область применимости ограничивалась указанными выше требованиями к степени намагниченности и ориентации материала во внешнем поле.

Поскольку мощные вычислительные способности современных компьютеров позволяют обойтись без большинства математических приближений и допущений, не так давно была начата разработка более строгой компьютерной модели гиромагнитного материала на основе частиц гексаферрита. Настоящая статья посвящена завершению и подведению итогов данной работы. В статье изложены основные идеи и принципы построения компьютерной модели, позволившие развить и обобщить существующую модель гиромагнитного материала на основе частиц гексаферрита на случай произвольных значений параметров, описывающих качество текстуры и пространственную ориентацию материала во внешнем магнитном поле, а также величину этого поля.

Физические основы компьютерной модели

При разработке обобщенной компьютерной модели в ее основу были положены физические представления и допущения, которые на сегодняшний день считаются известными и общепринятыми.

В частности, гиромагнитный материал на основе частиц гексаферрита представляется ансамблем неидентичных гексаферритовых частиц [7, 8]. В качестве модели реальной частицы используется модель однодоменной магнитно-одноосной частицы в форме эллипсоида вращения, ось симметрии которого совпадает с гексагональной осью кристалла [4]. Анизотропия магнитных свойств частиц учитывается посредством эффективного поля анизотропии [9]. Частицы в ансамбле отличаются друг от друга по ориентации в пространстве, размерам и по значению поля анизотропии [7, 8, 10]. Поведение вектора намагниченности частицы во внешнем магнитном поле подчиняется уравнению Ландау-Лифшица [11]. Высокочастотные магнитные свойства частицы описываются тензорами восприимчивости и проницаемости по слабому гармоническому магнитному полю. Расчет кривых перемагничивания и тензорных параметров материала осуществляется в приближении независимых зерен [7, 8].

К слову, эти же физические представления составляли основу приближенной теории ФМР. Однако, несмотря на использование одних и тех же исходных положений, обобщенная компьютерная модель позволяет рассмотреть случаи, прежде не доступные для количественного анализа по приближенной теории и созданной в ее рамках математической модели. Такая возможность появилась благодаря отказу от пути формального «переложения» громоздких формул [4] на электронную вычислительную технику и использованию при разработке обобщенной модели принципов имитационного компьютерного моделирования.

Основные принципы имитационного компьютерного моделирования в обобщенной модели гиромагнитного материала на основе частиц гексаферрита

В самых общих чертах метод имитационного компьютерного моделирования заключается в создании виртуальной модели реального объекта и имитации его поведения в условиях, приближенных к реальным, на основе фундаментальных физических закономерностей [12].

В частности, из упомянутого выше физического представления о гиромагнитном материале как ансамбле частиц следует, что имитационной компьютерной моделью гиромагнитного материала должен быть набор (массив) виртуальных гексаферритовых частиц.

Для имитации неидентичности частиц по геометрическим параметрам и магнитным свойствам виртуальные частицы в массиве наделяются различными (практически уникальными) наборами значений параметров, отвечающих за размеры и пространственную ориентацию, а также значение поля анизотропии каждой частицы. Такими параметрами у модели частицы являются объем , углы , поворота гексагональной оси в системе координат , связанной с внешним магнитным полем (рис. 1), намагниченность насыщения и константы поля анизотропии , .

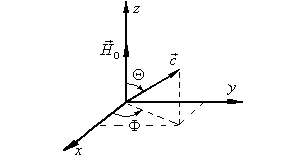
Рис. 1. Ориентация гексагональной оси частицы гексаферрита относительно внешнего магнитного поля

Наделение виртуальных частиц конкретными значениями параметров осуществляется в соответствии с общепринятым для описания зернистой структуры поликристаллических материалов подходом. Согласно этому подходу, пространственная ориентация, размеры и другие параметры частиц в материале полагаются случайными величинами [7, 8, 10] и описываются методами теории вероятностей. Для соответствия этому представлению используются специальные компьютерные процедуры, формирующие псевдослучайные последовательности с различными законами распределения, получившими распространение в литературе при описании распределения частиц по пространственной ориентации, размерам и значению поля анизотропии. Обращение к данным процедурам происходит при инициализации компьютерной модели; после формирования псевдослучайных последовательностей элементы каждой из них присваиваются соответствующим параметрам виртуальных частиц в ансамбле.

При определении значений параметров и считается, что ансамбль обладает аксиальной текстурой. Методика расчета значений параметров и заключается в определении направления оси (посредством углов и ) в системе координат , связанной с осью текстуры (рис. 2а), и его пересчете при известных углах и ориентации оси текстуры в систему координат (рис. 2б).

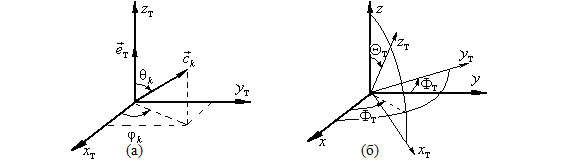
Рис. 2. Ориентация гексагональной оси частицы в системе координат (а), расположение системы координат во внешнем поле (б)

При моделировании, результаты которых приведены ниже, используются следующие законы распределения случайных величин:

, (1)

, (2)

, (3)

, (4)

где – параметр, характеризующий величину разброса пространственной ориентации частиц, , – средние значения первой константы поля анизотропии и объема частиц в ансамбле, , – дисперсии первой константы поля анизотропии и объема.

Такой подход обеспечил случайное изменение параметров частиц в ансамбле при переходе от одной частицы к другой и соответствие совокупности значений принятому для каждого параметра закону распределения (рис. 3); подробно алгоритмы работы процедур для формирования псевдослучайных последовательностей с указанными законами распределения описаны в [13, 14].

Рис. 3. Пример гистограмм распределений виртуальных частиц в ансамбле по пространственной ориентации (а, б), значению поля анизотропии (в) и объему (г) (сплошной линией показан график теоретически ожидаемого закона распределения)

Поскольку, как известно, магнитные свойства гексаферритов на КВЧ зависят от величины и направления постоянного магнитного поля, перед расчетом тензоров магнитных восприимчивости и проницаемости ансамбля необходимо провести расчет петли магнитного гистерезиса и выбрать на ней положение рабочей точки. Расчет петель гистерезиса ансамбля осуществляется при помощи специальной процедуры, разработанной для имитационного моделирования процесса перемагничивания частицы гексаферрита, изолированной от других частиц.

Разработка указанной процедуры проводилась с учетом двух основных физических представлений о процессе перемагничивания: во-первых, при отсутствии доменной структуры перемагничивание частицы происходит путем поворота вектора ее намагниченности под действием внешнего медленно меняющегося магнитного поля [15], во-вторых, перемагничивание характеризуется неоднозначностью и гистерезисом, т.е. зависимостью от магнитной истории системы «внешнее поле – частица».

Качественное объяснение неоднозначности (и гистерезиса) процесса перемагничивания однодоменной частицы гексаферрита довольно простое. Как следует из уравнения Ландау-Лифшица, в стационарном состоянии, когда внешнее магнитное поле неизменно, вектор намагниченности частицы занимает в пространстве такое положение, в котором происходит компенсация моментов сил, действующих на него со стороны внешнего магнитного поля и поля анизотропии частицы. Поскольку поле анизотропии в модели магнитно-одноосной частицы гексаферрита [4] имеет два возможных направления, противоположных друг другу, в общем случае для каждого из этих направлений стационарные положения вектора намагниченности будут разными.

Для имитации этой особенности при расчете кривых перемагничивания была разработана методика решения статической задачи (задачи о стационарном направлении вектора намагниченности частицы гексаферрита, помещенной в постоянное магнитное поле), в которой учитывается не только пространственная ориентация частицы и значения внешнего поля и поля анизотропии, но и информация о начальном направлении поля анизотропии [1].

Благодаря использованию данной методики при расчете кривых перемагничивания гистерезис проявляется как бы сам собой: при изменении напряженности поля в одних и тех же пределах кривые перемагничивания, получаемые при уменьшении и увеличении напряженности, получаются разными (рис. 4, по осям отложены величины , ).

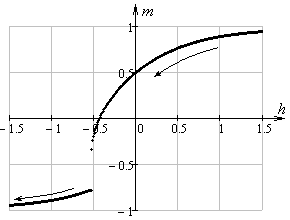
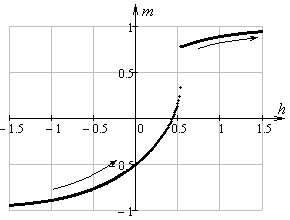
Рис. 4. Расчет кривых перемагничивания однодоменной частицы гексаферрита (, ) при уменьшении (слева) и увеличении (справа) напряженности внешнего поля

На основе этой методики были составлены алгоритм и компьютерная процедура расчета кривых перемагничивания ансамбля виртуальных частиц [14]. Благодаря отслеживанию и учету магнитной предыстории каждой частицы, кривые перемагничивания ансамбля, рассчитываемые при помощи данной процедуры, получаются зависящими от его начального состояния. Это дает возможность расчета не только предельных (относящихся к материалу, намагниченному до насыщения), но и частных петель гистерезиса.

Рис. 5. Пример расчета петель гистерезиса ансамбля (значения параметров модели: , , , кЭ, кЭ, , , кЭ)

На рис. 5 в качестве примера представлен график нормированных M―H петель гистерезиса, иллюстрирующий процессы намагничивания и перемагничивания изначально размагниченного ансамбля (при моделировании напряженность внешнего поля принимает следующие значения: кЭ).

Если при расчете кривых перемагничивания напряженность поля варьировать в других пределах, то, как и в реальном материале, изменится и конкретный вид частных петель гистерезиса. Таким образом, данная методика расчета кривых перемагничивания позволяет не просто получать при моделировании ансамбль в состоянии неполного (частичного) намагничивания, но и управлять этим состоянием, менять его числовые характеристики (например, значение намагниченности при нулевом внешнем поле). Подчеркнем, что указанная методика применима при любой пространственной ориентации частиц ансамбля во внешнем поле, поэтому с ее помощью можно рассчитывать петли гистерезиса ансамбля с произвольным качеством текстуры при произвольной ориентации оси текстуры во внешнем поле (рис. 6).

Рис. 6. Семейство петель гистерезиса при (а), (б), (в), (г), остальные параметры модели имеют такие же значения, что и на рис. 5

Указанная методика расчета кривых перемагничивания и петель магнитного гистерезиса создает основу, необходимую для расчета тензорных электродинамических параметров гиромагнитного материала в наиболее общем случае – при произвольных значениях геометрических и магнитных параметров частиц, а также параметров, отвечающих за качество текстуры и пространственную ориентацию материала и напряженность внешнего поля.

Расчет тензора магнитной восприимчивости материала по слабому гармоническому магнитному полю осуществляется путем усреднения тензоров магнитной восприимчивости всех содержащихся в ансамбле частиц. Расчет тензора магнитной восприимчивости каждой частицы осуществляется по формулам из [4], полученным в результате приближенного аналитического решения уравнения Ландау-Лифшица. Хотя использование готового аналитического решения несколько противоречит принципам имитационного моделирования, мы считаем этот шаг оправданным, поскольку в данном случае он позволяет экономить время при вычислениях[2].

При усреднении тензоров магнитной восприимчивости полагается, что частицы гексаферрита являются сильно анизотропными. Это допущение, обычно справедливое для магнитно-одноосных гексаферритов, применяемых в коротковолновой части миллиметрового диапазона, позволяет пренебречь магнитным взаимодействием частиц и работать в приближении независимых зерен [8]. Если при этом геометрические размеры ансамбля много меньше длины волны, явлениями распространения электромагнитного излучения можно пренебречь и считать, что на все частицы воздействует одинаковое магнитное поле.

В этом случае для расчета тензоров магнитных восприимчивости и проницаемости ансамбля в любой точке на любой петле гистерезиса можно воспользоваться методикой из [16]. Эта методика и указанная выше методика расчета петель гистерезиса позволяют рассчитать тензорные параметры, необходимые для компьютерного моделирования электродинамических процессов, в наиболее общем случае. Ниже представлены примеры моделирования, демонстрирующие влияние различных факторов на частотные характеристики материала. Отметим, что ранее строгий (в рамках принятых физических допущений) количественный расчет подобных характеристик по существующим математическим моделям [4, 5] не представлялся возможным.

Примеры моделирования

Для характеристик, представленных на рис. 7 – 9, расчет проводился при следующих фиксированных значениях параметров: кЭ, кЭ, , Гс, , . Значения остальных параметров указаны в конкретных примерах.

Пример 1. Влияние качества текстуры (рис. 7).

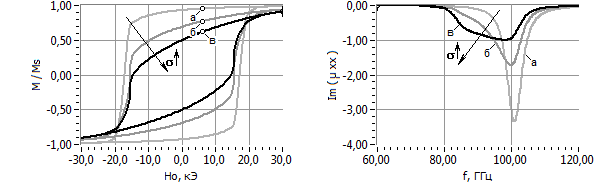
Рис. 7. К влиянию качества текстуры на характер предельных петель гистерезиса и резонансных кривых ансамбля

Значения параметров: , , , , , кЭ.

Как уже было сказано, параметр закона распределения (1) отвечает за разброс пространственной ориентации частиц в ансамбле. Таким образом, варьированием параметра можно управлять степенью пространственной упорядоченности частиц, т.е. качеством текстуры ансамбля.

Как видно из рис. 7, качество текстуры ансамбля влияет как на петли гистерезиса, так и на резонансные кривые. При ухудшении текстуры (в последовательности (а), (б), (в)) резонансная кривая расширяется, уменьшается по абсолютной величине резонансное значение мнимой части магнитной проницаемости, несколько уменьшается резонансная частота и увеличивается асимметрия кривой.

Пример 2. Влияние степени намагниченности ансамбля (рис. 8).

Рис. 8. К влиянию степени намагниченности ансамбля на резонансные характеристики

Значения параметров: , , , кЭ.

В левой части рис. 8 приведены предельная и частная петли гистерезиса, а также начальная кривая намагничивания. При нахождении на предельной петле гистерезиса (случаи (а), (д)) резонансные кривые в данном частотном диапазоне имеют один экстремум. Это говорит о преимущественной ориентации векторов статической намагниченности частиц в ансамбле, возникшей под действием «сильного» магнитного поля (напряженностью и кЭ соответственно). Однако в случае (а) внешнее поле направлено под острым углом (т.е. попутно) к вектору статической намагниченности ансамбля, потому резонанс наблюдается выше частоты естественного ФМР, оцениваемого в ГГц. В случае (д) внешнее поле направлено под тупым углом (т.е. встречно) вектору статической намагниченности ансамбля, поэтому резонанс наблюдается ниже частоты . Случаи (б), (в), (г) характеризуются наличием в ансамбле как частиц, для которых внешнее поле направлено попутно, так и частиц, для которых внешнее поле направлено встречно их намагниченности. Это приводит к появлению двух резонансных пиков, интенсивности которых зависят от соотношения количества тех или иных частиц.

Пример 3. Влияние постоянного магнитного поля (рис. 9).

Рис. 9. К влиянию постоянного магнитного поля на резонансные характеристики

Значения параметров: , кЭ, кЭ, , кЭ. Остальные параметры имеют те же значения, что и в примере 1.

При движении по верхнему участку предельной петли гистерезиса в сторону уменьшения напряженности внешнего поля (точки (а)-(б)-(в)-(г)) наблюдаются уменьшение резонансной частоты, изменение резонансного значения, ширины и степени асимметрии кривой. В окрестности нулевого поля резонансное значение мнимой части проницаемости достигает экстремального значения, ширина кривой минимальна. Изменяется асимметрия кривых: при внешнем поле, попутном вектору статической намагниченности ансамбля (случаи (а), (б)), более крутым является высокочастотный склон резонансной кривой, а при внешнем поле, встречном вектору статической намагниченности ансамбля (случай (г)) – более крутым оказался низкочастотный склон.

Заключение

Итак, в настоящей статье завершается работа по развитию и обобщению существующей математической модели гиромагнитного материала на основе частиц гексаферрита. Описаны основные идеи и принципы имитационного компьютерного моделирования, позволяющие рассчитать одни из главных электродинамических параметров материала – тензоры магнитных восприимчивости и проницаемости – при произвольных значениях параметров, отвечающих за качество текстуры и пространственную ориентацию материала во внешнем магнитном поле, а также за напряженность этого поля. Эти идеи реализованы в обобщенной компьютерной модели гиромагнитного материала на основе частиц гексаферрита. Проведен расчет резонансных кривых при варьировании качества текстуры материала и напряженности внешнего магнитного поля.

Созданная компьютерная модель может быть использована для решения задач компьютерного проектирования различных устройств КВЧ, содержащих гексаферритовые гиромагнитные резонаторы, а также для контроля гексаферритовых материалов методами радиоизмерений на миллиметровых волнах.

Авторы благодарны Кириллову А.И. за семинары по основам современной математики, по итогам которым у авторов возникло понимание основной идеи метода имитационного компьютерного моделирования и сформировалось общее представление о применении этого метода для создания компьютерной модели гиромагнитного материала на основе частиц гексаферрита.

Литература

1. Колодин П.С. Алгоритм расчета кривых перемагничивания однодоменной частицы гексаферрита // Журнал радиоэлектроники: электронный журнал. 2013. № 8. URL: http://jre.cplire.ru/jre/aug13/14/text.pdf (дата обращения: 17.09.2013).

2. Башилов Г. Беспроводные миллиметровые линии // Журнал сетевых решений/LAN. 2010. № 12. URL: http://www.osp.ru/lan/2010/12/13006840/ (дата обращения: 13.02.2014).

3. Китайцев А.А., Михайловский Л.К., Поллак Б.П., Ханамиров А.Е. Абсорбционные применения гексаферритов // Междунар. науч.-техн. конф. к 100-летию со дня рождения В.А. Котельникова: Москва, 21–23 октября 2008: Тез. докл. М.: Издательский дом МЭИ, 2008. С. 53–55.

4. Pollak B.P., Hanamirow A.E., Korneew I.W. Mono- und polykristalline hexagonale Ferrite als Materialien fuer Resonanzeinrichtungen in der Mikrowellentechnik // Nachrichtentechnik Elektronik. 1976. B. 26. H. 7. S. 245–250.

5. Поллак Б.П. Анализ особенностей тензора магнитной восприимчивости поликристаллического гексаферрита // Тр. Моск. энерг. ин-та. 1977. Вып. 320. С. 45–53.

6. Раков А.В. Программная реализация математической модели гексаферритового гиромагнитного резонатора // Сб. тр. XVII Международной конференции «Магнетизм, дальнее и ближнее спин-спиновое взаимодействие». М.: ПЛАНТИ, 2009. С. 315–320.

7. Stoner E.C., Wohlfarth E.P. A mechanism of magnetic hysteresis in heterogeneous alloys // Phil. Trans. R. Soc. А. 1948. № 240 (826). P. 599–642.

8. Schloemann E., Jones R.V. Ferromagnetic resonance in polycrystalline ferrites with hexagonal crystal structure // J. Appl. Phys. 1959. V. 30. 177S–178S.

9. Kittel C. On the theory of ferromagnetic resonance absorption // Phys. Rev. 1948. V. 73. P. 155–161.

10. Михайловский Л.К., Поллак Б.П., Балаков В.Ф. Свойства поликристаллических гексаферритов и особенности их работы в СВЧ устройствах // XIV. Intern. Wiss. Koll. TH Ilmenau, 1969. H. 3. S. 135–138.

11. Ландау Л.Д., Лифшиц Е.М. К теории дисперсии магнитной проницаемости ферромагнитных тел // Собр. тр. Л.Д. Ландау / Под ред. Е.М. Лифшица. М.: Наука, 1969. Т. 1. С. 128–143.

12. Шеннон Р. Имитационное моделирование систем – искусство и наука / Пер. с англ.; под ред. Е.К. Масловского. М.: Мир, 1978. 420 с.

13. Колодин П.С. Способы формирования псевдослучайных последовательностей для имитации неодинаковой пространственной ориентации частиц в компьютерной модели поликристаллического гексаферритового материала // Сб. тр. XXI Международной конференции «Электромагнитное поле и материалы (фундаментальные физические исследования)». М.: РПЦ Офорт, 2013. С. 463–482.

14. Колодин П.С., Поллак Б.П. Алгоритм расчета кривых перемагничивания ансамбля однодоменных частиц гексаферрита // Сб. тр. XXI Международная конференция «Электромагнитное поле и материалы (фундаментальные физические исследования)». М.: РПЦ Офорт, 2013. С. 483–500.

15. Акулов Н.С. Ферромагнетизм. М.-Л.: Гос. изд-во технико-теоретич. лит., 1939. 188 с.

16. Колодин П.С., Поллак Б.П. Вероятностная компьютерная модель гиромагнитного материала на основе частиц гексаферрита // Сб. докл. I Всероссийской микроволновой конференции. М.: Изд-во ИРЭ им. В.А. Котельникова РАН, 2013. С. 54–58.

[1] К их числу относятся как образцы различной формы (пластины, шайбы и др.), изготовленные из спеченных гексаферритовых поликристаллов, так и тонкие пленки из композиционных гексаферритовых материалов.

[2] По сравнению с имитационным методом, включающим численное решение уравнения Ландау-Лифшица, выделение из решения первой гармоники прецессии вектора намагниченности и определение ее параметров.