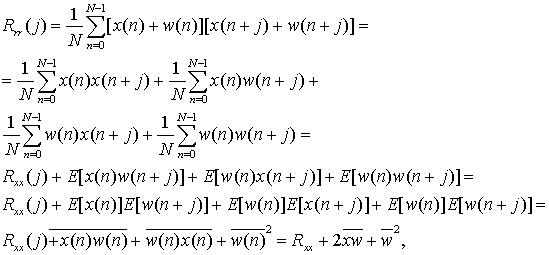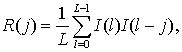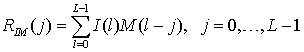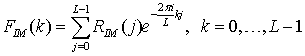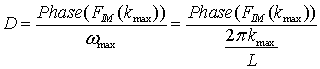УДК 621.391

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ БЫСТРО ДВИЖУЩЕГОСЯ МАЛОКОНТРАСТНОГО ОБЪЕКТА НА ЗАШУМЛЕННОМ ИЗОБРАЖЕНИИ

А. П. Трещалин, И. С. Осадчий, В. П. Богданов

Московский Физико-технический институт (государственный университет)

Статья получена 13 марта 2014 г.

Аннотация. Рассматривается задача определения положения быстро движущегося объекта на зашумленном изображении, полученном с помощью ПЗС камеры. Применение преобразования Радона позволяет выделить траекторию движения. Преобразование Фурье от автокорреляции вдоль найденной траектории дает возможность найти скорость движения в плоскости изображения. По найденной скорости, с учетом особенностей работы ПЗС камеры, строится модель движения. По максимуму корреляции находится начальное положение объекта. Разработана модель системы, и с ее помощью получены оценки достижимой точности определения положения объекта при различных отношениях сигнал/шум.

Ключевые слова: быстро движущийся объект, зашумленное изображение, преобразование Радона, автокорреляция, взаимная корреляция, компьютерная модель.

Abstract. The problem of determining the position of a fast moving object in a noisy image obtained using the CCD is considered. Application of Radon transform allows to select the motion path. Fourier transformation of autocorrelation along the trajectories obtained allows to find the speed in the image plane. Using this speed and taking into account features of CCD it is possible to construct the motion model. Maximum correlation is the initial position of the object. A model of the system is worked-out, which permits to obtain estimates of achievable accuracy of the object location at different signal/noise ratios.

Keywords: fast moving object, a noisy image, Radon transform, autocorrelation, cross-correlation, the computer model.

Введение

В настоящее время происходит непрерывный рост числа объектов «космического мусора», то есть вышедших из строя летательных аппаратов и их фрагментов, остающихся на околоземной орбите. Одним из способов поискатаких объектов являетсясоздание оптико-электронных устройств, состоящих из оптической системы, ПЗС-матрицы и алгоритмов автоматического детектирования [1]. Фрагменты «космического мусора» на видеоизображении проявляются как быстро движущиеся и малоконтрастные элементы за счет слабого оптического сигнала, отраженного от их поверхности и попадающего на плоскость ПЗС-матрицы. В связи с этим, основной проблемой разработки методов и алгоритмов обнаружения и нахождения координат объектов является достижение как можно меньшего порога соотношения сигнал/шум, при котором происходит выделение объектов на изображении.

Варианты решения проблемы предлагались в работах [2] – [4]. В [2] рассматривается задача обнаружения и оценки координат астероидов на серии ПЗС кадров, при этом предполагается, что на формируемых ПЗС-матрицей кадрах изображение астероида идентично изображению звезд. Кроме того, определение положения астероида на изображении основано на локальной статистике, полученной при внутрикадровой обработке. Работа [3] посвящена цели улучшения изображения треков, полученных при пороговой обработке кадров. В [4] предлагается использовать локальную фильтрацию для сглаживания изображения. Так как съемка предполагает большие времена экспозиции, после пороговой обработки строится непрерывная траектория. Оценка координат конечных положений строится по максимуму локальной корреляции сигнала и модели.

Все рассмотренные методы и алгоритмы строятся на локальной обработке изображений и, следовательно, могут работать только при больших отношениях сигнал/шум. В данной статье описан метод, основанный на статистической обработке, что обеспечивает его работоспособность при значительно меньших отношениях сигнал/шум.

Постановка задачи

Для видео фиксации пространства используется оптическая система, проецирующая сигнал на плоскость ПЗС-матрицы. ПЗС-матрица имеет фиксированный кадровый период , где – время накопления заряда, в течении которого формируется изображение, – межкадровый интервал, в течении которого фотоприемники неактивны и отсутствует накопления заряда. В процессе работы , и не изменяются. ПЗС-матрица имеет собственный шум накопления заряда, который может иметь различные характеристики. Для формирования дискретного изображения из накопленных ПЗС-матрицей зарядов используется аналого-цифровой преобразователь, который так же добавляет шумовую составляющую на изображение.

В поле зрения оптической системы находится один исследуемый объект. На видеоизображении движение данного объекта является прямолинейным и равномерным. При этом, скорость объекта и величина оптического сигнала, попадающего на плоскость ПЗС-матрицы, могут быть различными.

Необходимо определить траекторию движения и начальное положение объекта на изображении при различных вариантах соотношения сигнал/шум. За сигнал принимается световой поток, отраженный от исследуемого объекта, прошедший через оптическую систему и попавший на плоскость ПЗС-матрицы. Шум состоит из собственных шумов ПЗС-матрицы и шума квантования АЦП.

Основные этапы

Предлагаемый метод использует последовательность кадров для определения траектории и положения исследуемого объекта на изображении. Для выделения основных этапов рассмотрим процесс формирования последовательности кадров оптико-электронной аппаратурой.

Световой поток собирается оптической системой и фокусируется на плоскость фотоприемника, который преобразует падающие фотоны в электроны. В течение времени экспозиции происходит накопление фотоэлектронов в ячейках ПЗС-матрицы. По окончанию времени за время заряд переносится в вертикальные регистры. Затем из вертикальных регистров заряд переносится в горизонтальные регистры и попадает на выход ПЗС-матрицы в виде напряжения. Напряжение подается на АЦП, где происходит квантование уровней напряжений.

Исходя из этого, изображение траектории на последовательности кадров будет представлять собой прямую пунктирную линию. Длинна штрихов (накопленного сигнала) будет составлять , а расстояние между ними (упущенного сигнала) , где – скорость движения объекта на изображении.

Учитывая специфику работы оптико-электронного преобразователя, предлагаемый метод можно разделить на 3 ключевых этапа:

I. Детектирование траектории движения. Траектория исследуемого объекта рассматривается как непрерывная линия, поиск которой производится по всей площади видеоизображения;

II. Оценка скорости движения. Для найденного положения трека на видеоизображении производится расчет скорости движения объекта в плоскости ПЗС-матрицы с учетом реальной формы трека;

III. Поиск начального положения объекта. На основе найденного трека объекта и его скорости производится расчет начального положения в последовательности кадров.

I. Детектирование траектории движения

Для поиска трека объекта на последовательности изображений как непрерывной линии применимы ранее разработанные алгоритмы. Наиболее популярными из них являются Преобразование Хафа [5] и Преобразование Радона [6].

Преобразование Хафа. Зададим прямую на изображении двумя параметрами: – расстояние от прямой до начала координат, – угол между внешней нормалью прямой и осью абсцисс.

Уравнение прямой записывается через параметры следующим образом:

, (1)

где x, y – координаты точки на изображении.

Уравнение (1) устанавливает отображение из множества прямых на изображении во множество точек плоскости параметров . С другой стороны, каждой точке на изображении соответствует синусоида в пространстве параметров, задаваемая уравнением (1), причем каждая точка на этой синусоиде соответствует некоторой прямой, проходящей через .

Разделим пространство параметров на ячейки. Каждая ячейка представляет собой счетчик. Количество ячеек определяется требуемой точностью определения прямой и требованиями к быстродействию вычисления. Для каждой точки изображения построим синусоиду в пространстве параметров с яркостью, пропорциональной яркости точки изображения . Увеличим счетчики ячеек, через которые прошла синусоида, на яркость синусоиды. Если счетчик ячейки с центром имеет большое численное значение, то на изображении есть много ярких точек, лежащих на прямой с параметрами, близкими к .

Преобразование Радона. Преобразование Радона также формирует пространство параметров. Для непрерывной функции преобразование Радона получается интегрированием значений функции вдоль наклонных прямых и определяется следующим образом:

, (2)

где –угол между внешней нормалью прямой и осью абсцисс, – расстояние от прямой до начала координат и – максимальное расстояние.

Данное преобразование отображает пространство изображения в пространство параметров . Величина шага изменения параметров ипрямо пропорциональна скорости обработки и обратно пропорциональна точности определения прямой.

Для вычисления преобразования Радона разработаны эффективные алгоритмы. В работе [7] приведён алгоритм вычисления быстрого преобразования Радона, основанный на рекурсивном вычислении интегралов вдоль прямых. Для изображения из точек вычисляются интегралов вдоль “базисных” прямых, а затем показывается, что интеграл вдоль любой прямой может быть выражен через сумму не более чем интегралов вдоль “базисных” прямых. Его сложность составляет . Однако в процессе работы алгоритма строится граф, содержащийвершин и ребер, что предъявляет чрезмерные требования к памяти. В [8] предложен способ быстрого вычисления преобразования Радона через двумерное преобразование Фурье, а в статье [9] - через двумерное преобразование Хартли. Сложность этих алгоритмов составляет .

Для определения на изображении линии, по которой проходит трек исследуемого объекта воспользуемся преобразованием последовательности кадров ПЗС-матрицы в пространство Радона. При этом за параметры линии, соответствующей треку, будем принимать такие параметрыпространства Радона, величина ячейки которых максимальна.

II. Оценка скорости объекта

Выделенный трек исследуемого объекта имеет периодическую структуру в виде пунктирной линии на последовательности изображении за счет специфики работы ПЗС-матрицы. Скорость движения данного объекта можно вычислить как отношение периода трека к времени получения одного кадра. Так как время фиксировано, то необходимо найти период трека.

Как известноиз [10], дискретный сигнал можно выразить как сумму полезного сигнала и шума :

(3)

где – количество отсчетов сигнала.

Так как полезный сигнал и шум не коррелируют, автокорреляционную функцию можно записать следующим образом:

(4)

где N – количество отсчетов исходного сигнала r, –автокорреляционная функция полезного сигнала x.

Отсюда видно, что автокорреляционная функция зашумленного сигнала состоит из автокорреляционной функции полезного сигнала, на которую накладывается затухающая функция, зависящая от случайного компонента и полезного сигнала. Очевидно, что автокорреляционная функция периодического сигнала также будет периодической.

Представим найденные отсчеты на видеоизображении, относящиеся к треку исследуемого объекта, как одномерный массив , содержащий значений. Тогда автокорреляционная функция будет выражаться следующим образом:

где . (5)

Для нахождения периоданадо вычислить преобразование Фурье полученной автокорреляционной последовательности. Преобразование Фурье будет выражаться следующим образом:

, (6)

где –комплексные амплитуды синусоид (гармоник), на которые разлагается вычисленная автокорреляционная последовательность. Самая большая ненулевая гармоника будет соответствовать периоду трека исследуемого объекта.

В результате использования преобразованияФурьеот автокорреляционной функции удается снизить воздействие шумовой составляющей,что приводит к уменьшению вероятности ложного определения и повышает точность вычисление периода трека исследуемого объекта.

III. Поиск начального положения объекта

Поиск начального положения объекта на найденном треке является родственной по отношению к классической задаче в области обработки сигналов: определение задержки отраженного сигнала радара [11], [12].

Пусть передан сигнал . Тогда принимаемый можно записать

, (7)

где– коэффициент ослабления, – задержка прихода сигнала, – шумовая составляющая принимаемого сигнала.

Для корреляции передаваемого и принимаемого сигналов имеем

, (8)

где – автокорреляционная функция сигнала , – корреляционная функция переданного сигнала и шумовой составляющей принятого сигнала.

Исходя из (4) видно, что корреляционная функция передаваемого и зашумленного принимаемого сигнала состоит из автокорреляционной функции полезного сигнала, на которую накладывается затухающая функция, зависящая от случайного компонента и полезного сигнала.

Следовательно, оптимальная оценка задержки состоит в нахождении максимума функции корреляции передаваемого и принимаемого сигналов. По положению максимума функции корреляции можно определить задержку.

Так же существует другой подход к определению задержки между передаваемым и принимаемым сигналами. Найдем преобразование Фурье корреляциипередаваемого и зашумленного принимаемого сигнала

. (9)

Учитывая, что передаваемый сигнал и аддитивный шум не коррелируют, получаем оценку

. (10)

Теперь имея оценку кросс-спектральной функции передаваемого и принимаемого сигналов, можем оценить временную задержку из ее фазы:

. (11)

В задаче определения начального положения объекта на изображении вдоль траектории временной задержке соответствует смещение вдоль траектории, передаваемому сигналу – модель видимого движения.

Сначала по найденной скорости видимого движения и с учетом особенности структуры последовательности ПЗС кадров необходимо построить ожидаемое изображение движущегося объекта. Если функцию рассеяния точки аппроксимировать гауссианой, то модель видимого движения можно построить в соответствии с формулой:

. (12)

Осталось найти начальное положение объекта на найденной траектории. Для этого находим корреляцию полученного шаблона и массива яркостей точек вдоль прямой

. (13)

Находим преобразование Фурье полученной корреляционной функции

. (14)

Находим частоту, которой соответствует максимум абсолютной величины:

. (15)

По фазе на этой частоте находим положение объекта:

. (16)

Построение модели

Для исследования, оценки работоспособности и определения минимального соотношения сигнал/шум по предлагаемому методу была разработана модель в среде MATLAB.

Моделирование поступающих на вход данных производилось для 100 вариантов изображений с разными соотношениями сигнал/шум. Размер каждого изображения составляет 1120 на 612 пикселей. На Рисунке 1 показаны фрагменты моделируемых видеоизображений с разными соотношениями сигнал/шум и содержащие трек от исследуемого объекта:


a)	б)	в)
Рисунок 1. Моделируемые фрагменты изображения: а) – сигнал/шум равен 1, б) сигнал/шум равен 2, в) сигнал/шум равен 3.

На Рисунке 2 показан результат работы первого этапа метода для одного из смоделированных видеоизображений:

б)

в)

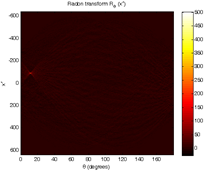
Рисунок 2. а) – исходное видеоизображение, б) – отображение в пространство Радона, в) – найденный трек.

Рисунок 2,а представляет собой исходные данные, которые поступают на вход разработанной модели. Рисунок 2,б является графическим представлением преобразования исходных данных в пространство Радона по формуле (2). Рисунок 2,в отображает найденную траекторию исследуемого объекта. Из Рисунков 2,a и 2,в видно, что найденная траектория совпадает с траекторией исходного изображения.

Основные результаты этапа определения скорости исследуемого объекта изображены на Рисунке 3:


a)	б)	в)
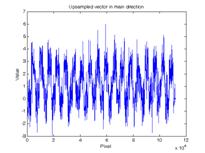
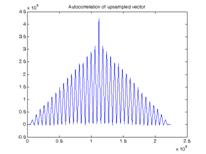
Рисунок 3. а) – исходные значения трека, б) – автокорреляционная функция в) – абсолютные значения коэффициентов преобразования Фурье автокорреляции.

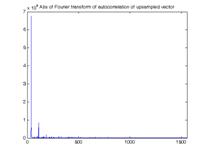
На Рисунке 3,а показаны значения изображения вдоль найденного трека. Автокорреляционная функция (5) данных значений показана на Рисунке 3,б. Абсолютные значения преобразования Фурье от автокорреляционной функции (6) представлены на Рисунке 3,в, из которого видно, что существует ярко выраженная ненулевая гармоника, которая соответствует скорости исследуемого объекта.

Этап нахождения начального положения изображен на Рисунке 4:


a)	б)	в)	г)
Рисунок 4. Нахождение начального положения: а) – построенная модель видимого движения, б) – взаимная корреляция значений вдоль найденной прямой, в) – абсолютные значения коэффициентов преобразование Фурье от корреляции, г) – фазовый сдвиг.

По найденной скорости исследуемого объекта строится модель видимого движения в соответствии с формулой (12). Результат построения показан на Рисунке 4,а. Для исходных значений вдоль трека и построенной модели вычисляется корреляция (13) (изображена на Рисунке 2,б). Для найденной корреляции вычисляется преобразование Фурье (14), результаты которого показаны на Рисунках 4,в и 4,г. С помощью соотношений (15) и (16) устанавливается начальное положение объекта.

Основные результаты исследования разработанной модели на основе предлагаемого метода отображены на Рисунках 5 и 6.

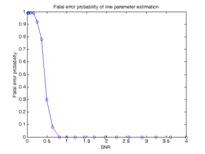
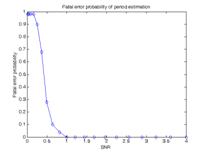
На Рисунке 5 показана зависимость фатальной ошибки работы этапов модели от соотношения сигнал/шум на смоделированных изображениях. В качестве критерия фатальной ошибки принималось отклонение более чем на 5 пикселей от исходной траектории исследуемого объекта.


a)	б)	в)
Рисунок 5. Вероятность фатальной ошибки в зависимости от соотношения сигнал/шум: а) – определение положения траектории, б) – скорости видимого движения, в) – начального положения траектории.

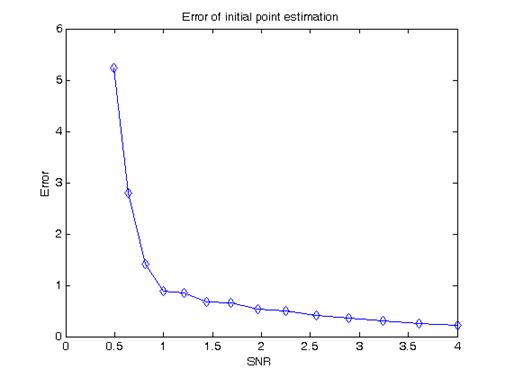
На Рисунке 6 показана зависимость среднеквадратичной ошибки определения координат объекта (в пикселях) от отношения сигнал/шум:

PointEstimationError

Рисунок 6. Зависимость среднеквадратичной ошибки определения координат объекта (в пикселях) от отношения сигнал/шум.

Из представленного рисунка видно, что при соотношении сигнал/шум больше 1 среднеквадратичная ошибка не является фатальной.

Выводы

Задача обнаружения и оценки координат быстро движущегося объекта на серии ПЗС кадров рассмотрена с точки зрения статистических методов обработки сигналов. Показано, что исходную задачу можно разбить на три следующих задачи: сначала надо найти прямую, на которой лежит траектория, затем определить скорость видимого движения вдоль найденной прямой и, наконец, определить начальное положение объекта на найденной траектории.

Для нахождения траектории целесообразно использовать преобразование Радона. Показано, что основные задачи имеют много общего с классическими задачами оптимального оценивания параметров сигнала на фоне шумов.

Разработанная модель позволяет определить граничное значение отношения сигнал/шум для разработанных алгоритмов. Кроме того, модель позволяет оценить точность определения положения объектов на серии ПЗС кадров в зависимости от отношения сигнал/шум.

Данные, полученные в результате моделирования, позволяют сделать вывод о том, что рассмотренный метод может применяться к изображениям с отношением сигнал/шум порядка 1, что как минимум на 3 дБ ниже, чем требуется для работы обычных алгоритмов.

Литература

1. Трещалин А.П. Применение оптико-электронной аппаратуры космических аппаратов для предварительного определения параметров орбит околоземных объектов // Труды МФТИ. — 2012. —Т. 4, № 3. — С. 122–131.

2. Оценка координат астероида на дискретном изображении. В.Е Саваневич, А.Б. Брюховецкий, А. М. Кожухов, Е. Н. Диков.// Радиотехника: Всеукр. межвед. науч.-техн. сб. 2010. Вып. 162. С. 78 — 86.

3. Gusyatin, O. “Novel Segmentation Technique to Enhance Detection of Fast Moving Objects with Optical Sensors.” Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, held in Wailea, Maui, Hawaii, September 14-17, 2010.

4. Simms L., Riot V., DeVries W., Olivier S. S., Pertica A., Bauman B. J., Phillion D., Nikolaev S. “Optical Payload for the STARE Mission.” SPIE Defense And Security, Orlando, FL, United States, Apr 25 - Apr 29, 2011.

5. Princen J.P., Illingworth, J. and Kittler, J.V., “A Formal Definition of the Hough Transform: Properties and Relationships”, Journal of Mathematical Imaging and Vision, 1992, vol.1, num.1, pp.153-168.

6. Toft P.A., “The Radon Transform: Theory and Implementation”, PhD Thesis, Technical University of Denmark, 1996.

7. David Donoho, XiaomingHuo, “Applications of Beamlets to Detection and Extraction of Lines, Curves and Objects in Very Noisy Images”, Nonlinear Signal and Image Processing (NSIP), 2001.

8. CheyneGaw Ho, Rupert C. D. Young, Chris D. Bradfield, Chris R. Chatwin, “A Fast Hough Transform for the Parametrisation of Straight Lines using Fourier Methods”, Real-Time Imaging, 2000, vol.6, num.2, pp.113-127.

9. Volegov D.B., Gusev V.V., Yurin D.V. “Straight Line Detection on Images via HartleyTransform. Fast Hough Transform”, 16-th International Conference on Computer Graphics and Application GraphiCon'2006, July 2006, Novosibirsk, Akademgorodok, Russia.

10. Айфичер Э.С., Джервис Б.У. Цифровая обработка сигналов: практический подход, 2-е издание.: пер. с англ. - М.: Издательский дом "Вильямс", 2004. - 992 с

11. Перов А.И. Статистическая теория радиотехнических систем. Учеб. пособие для вузов. – М.: Радиотехника, 2003. – 400с.

12. Тихонов В. И. Оптимальный приём сигналов. — М.: Радио и связь, 1983. — 320с.