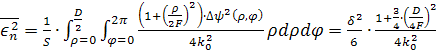ИССЛЕДОВАНИЕ ВЛИЯНИЯ РЕГУЛЯРНЫХ ФАЗОВЫХ ОШИБОК НА ХАРАКТЕРИСТИКИ ЗЕРКАЛЬНОЙ ПАРАБОЛИЧЕСКОЙ АНТЕННЫ С ЭЛЕКТРИЧЕСКИМ СКАНИРОВАНИЕМ

 

Е. И. Лаврецкий ¹, В. С. Чернышов ²

¹ ОАО «МКБ Компас», Москва

² ОАО НИИ Точных Приборов, Москва

 

Статья получена 11 марта 2015 г.

 

Аннотация. Разработана электродинамическая модель и проведено численное исследование приемной зеркальной антенны с коническим рупором, в котором распространяются основная и высшие моды. Получены графики зависимостей амплитуд и фаз волн , ,  и  при коническом сканировании вокруг фокальной оси как для рефлектора с профилем идеального параболоида вращения, так и для рефлектора с регулярными отклонениями отражающей поверхности от идеального параболоида. Показано, что нарушения фазового распределения в антенне приводят к осцилляциям амплитуд и фаз принимаемых волн и, в результате, к нарушениям пеленгационной характеристики антенны. Установлен уровень допустимой фазовой ошибки на краю раскрыва, соответствующий уменьшению амплитуд высших мод в некоторых угловых направлениях на ≈3 дБ. Рассчитано допустимое среднеквадратическое отклонение отражающей поверхности зеркала для антенны с электрическим сканированием.

Ключевые слова: зеркальная параболическая антенна, регулярные фазовые ошибки, электрическое сканирование, пеленгационная характеристика, конический рупор, высшие моды.

Abstract: The electrodynamic model was developed and the numerical investigation was performed for a receiving mirror antenna having a multimode conical horn as a fed. We obtained graphs of dependences of magnitudes and phases for circular horn modes , ,  and  during conical scanning around the antenna focal axis. Analysis was performed both for the reflector with a shape of an ideal paraboloid of revolution, and for the same paraboloid with regular surface distortions. It was shown that the phase distortions in antenna produce the oscillations of magnitudes and phases of received horn modes and, as a result, create the distortions of the bearing characteristic of the auto-tracking antenna. We found the maximum allowed level of the phase error giving the 3-dB decrease of the higher modes magnitudes for some angle directions. We estimated the maximum allowed root-mean square deviation of paraboloid reflector surface for using in the auto-tracking mirror antenna.

Key words: a mirror parabolic antenna, regular phase errors, auto-tracking, a circular conical horn, high-order modes.

 

1. Введение

         В земных станциях спутниковой связи в настоящее время широко используются зеркальные антенны с электрическим сканированием (с автоматическим сопровождением). На частотах ниже 10 ГГц эффект Фарадея в атмосфере приводит к существенному повороту плоскости поляризации волны, поэтому прием информации со спутника на этих частотах осуществляется, как правило, на круговой поляризации [1]. Круговая поляризация используется и для более высоких частот, в [2] сообщается о разработке облучателя зеркальной антенны с возможностью автосопровождения на круговой поляризации в Ка-диапазоне (≈32 ГГц). Распространенным типом облучающего устройства зеркальной антенны с электрическим сканированием является металлический рупор, в котором падающая волна возбуждает основную моду и несколько высших волноводных мод. Основная мода используется для формирования суммарной диаграммы направленности (ДН), одна или несколько высших мод используются для формирования разностной ДН [3-7]. Для осесимметричной зеркальной системы естественной формой рупора является круглый конический рупор, в котором основной модой является волна , а используемыми для формирования разностной ДН высшими модами являются волны ,  и . Волны  и  имеют по две ортогональных поляризации. При приеме круговой поляризации поля от вертикальной и горизонтальной поляризаций волны  объединяются в поляризаторе (или квадратурном мосте). В литературе описаны различные варианты выбора высших мод для создания облучателя антенны с электрическим сканированием ДН. Например, в [3-5] предложено использовать для формирования разностной ДН волну  (одной или двух поляризаций). Если электрическое сканирование осуществляется с помощью двух поляризаций волны , то они могут быть объединены с помощью квадратурного моста. В [6] запатентован облучатель, принимающий одновременно волны ,  и . В [7] сообщается о разработке облучателя зеркальной антенны, в котором используются для электрического сканирования волны  и . Способы формирования пеленгационной характеристики антенны и сигналов ошибки исходя из суммарной и разностной ДН подробно описаны в специальной литературе.

         Погрешности выполнения отражающих поверхностей зеркальных антенн приводят к нарушениям амплитудно-фазового распределения в раскрыве и влияют на их характеристики излучения. Эти погрешности могут носить как статистический, так и детерминированный характер [8,9]. В литературе проведено исследование влияния погрешностей на такие параметры ДН антенны, как коэффициент усиления, уровень боковых лепестков и кроссполяризационного излучения. При этом обычно всегда рассматривалась диаграмма направленности типа суммарной ДН, имеющая один главный лепесток. В известной авторам литературе отсутствует систематическое исследование влияния погрешностей рефлектора на характеристики зеркальной антенны с электрическим сканированием, имеющей суммарную и разностную ДН.

         Разработчик антенной системы при выборе рефлектора обычно задает допустимую фазовую ошибку, которая является главной причиной снижения коэффициента усиления. Например, в [10] указано, что при определении точности изготовления зеркала исходят из допустимой фазовой ошибки в раскрыве, равной . Априори неясно, можно ли использовать такое зеркало в антенне с электрическим сканированием или должны быть предъявлены более жесткие требования. В данной статье в рамках математической модели было проведено исследование влияния регулярных фазовых ошибок на амплитуды и фазы волн, возбуждаемых в многомодовом коническом рупоре облучателя зеркальной антенны. Фазовая ошибка в раскрыве зеркала была транслирована в искажения отражающей поверхности рефлектора. Антенна анализировалась в приемном режиме, когда на нее падала волна от источника в дальней зоне при коническом сканировании вокруг фокальной оси зеркала.

 

2. Математическая модель

         Характеристики направленности антенны при наличии регулярных отклонений отражающей поверхности рефлектора могут быть напрямую определены прямыми вычислениями интеграла Кирхгофа, в фазовой функции которого учтены регулярные фазовые ошибки [9], что является исследованием антенны в режиме передачи. Для антенны с электрическим сканированием в таком подходе потребовалось бы проводить раздельные расчеты при каждом виде возбуждения в облучателе (разными модами), а затем каким-то способом комбинировать результаты. Поэтому представляется удобнее рассмотреть антенну с электрическим сканированием в режиме приема, как она работает в реальности, когда на антенну падает плоская волна (поле от источника в дальней зоне), чтобы получить результаты по всем интересующим нас модам облучателя одновременно.

         На рисунке 1 показана геометрия рассматриваемой приемной зеркальной антенны и система мод рупора. Антенна имеет металлический рефлектор в виде параболоида вращения с диаметром D и фокусным расстоянием F. В фокусе рефлектора установлен облучатель в виде конического рупора с диаметром раскрыва D_fed, в котором могут распространяться волны , ,  и . В качестве стороннего источника был рассмотрен сферический источник в дальней зоне антенны, расположенный в окрестности фокальной оси рефлектора. Источник вращался по кругу вокруг фокальной оси под углом α.

 

 

 

 

Рис.1- Геометрия приемной зеркальной системы и система мод рупора

 

 

         Для анализа данной структуры использовалась математическая модель на основе метода физической оптики. Поле стороннего источника возбуждает поверхностный электрический ток на металлическом рефлекторе антенны , где  – нормаль к поверхности рефлектора. Электрический ток на рефлекторе возбуждает поперечное поле  в раскрыве рупора облучателя. В приближении отсутствия отражений в раскрыве рупора мощности принятых волн можно записать в виде

                             , для  – волн                         (1)

                            , для  – волн,

 

фазы принятых волн можно записать в виде

                            ,        для  – волн,                          (2)

                            ,        для  – волн,

 

где  – скалярные произведения между поперечным магнитным полем в раскрыве рупора  и ортонормированными функциями разложения поперечного магнитного поля ;  Ом- волновое сопротивление свободного пространства, λ- длина волны в вакууме, λ_g – длина волны в волноводе, диаметр которого равен раскрыву рупора. Скалярные произведения  и  могут быть рассчитаны численным интегрированием по апертуре.

         Ортонормированные функции разложения поперечного магнитного поля для  и  -волн в волноводе круглого сечения имеют вид [11]:

  ,        (3)

 ,

 

где нормировочные множители равны

             ,  ,               (4)

 

 – функция Бесселя 1-го рода, ,  – символ Кронекера,  – радиус круглого волновода.

         В (3) верхние и нижние строки в квадратных скобках соответствуют двум разным поляризациям при одинаковых индексах (n,m). Моды, соответствующие верхним строкам в квадратных скобках, будем обозначать  и , поскольку они произошли от скалярной собственной функции с азимутальной зависимостью ; моды, соответствующие нижним строкам в квадратных скобках, будем обозначать  и , так как они произошли от скалярной собственной функции с азимутальной зависимостью  [11]. Если n=0, то существуют только поляризации, соответствующие верхним строкам, для них символ cos опускаем (например, волны  и ). На рисунке 1 показаны все рассматриваемые моды, для которых указаны направления векторов электрического поля, соответствующих функциям магнитного поля (3). Заметим, что  есть основная мода круглого волновода с вертикальной поляризацией,  – основная мода с горизонтальной поляризацией.

         Математическая модель позволяет проводить расчеты для произвольного рефлектора- как для идеального параболоида вращения, так и для искаженного рефлектора. В качестве модели регулярных фазовых искажений в раскрыве антенны задавалась ошибка, имеющая аналитическую форму:

                                    ,                                                      (5)

 

где - максимальная фазовая ошибка на краю рефлектора, (ρ,φ)- полярные координаты, n- индекс азимальной гармоники фазовых искажений. Рассмотрение было ограничено четными n, при которых фазовая ошибка симметрична относительно центра рефлектора. При таких фазовых ошибках не изменяется направление оси ДН, которая направлена вдоль фокальной оси рефлектора. Фазовая ошибка (5) является квадратической по радиальной координате и служит аппроксимацией возникающих на практике искажений для зеркал, состоящих из жесткой центральной части и периферийных лепестков, когда искажения в центральной части малы.

         При данном виде фазовой ошибки имеем одинаковую среднеквадратическую фазовую ошибку при любом n≠0. Средний квадрат фазовой ошибки по раскрыву равен

                             ,                       (6)

 

откуда среднеквадратическая фазовая ошибка равна

                            .                                                                                         (7)

         Для проведения расчетов по методу физической оптики фазовые ошибки в раскрыве были транслированы в регулярные отклонения от идеального параболоида. Для этого использовалась связь фазовой ошибки в раскрыве с отклонением отражающей поверхности параболоида от идеальной по нормали к поверхности:

                                     ,                                                                        (8)

где - отклонение отражающей поверхности по нормали,  – волновое число в свободном пространстве.

         При известном аналитическом задании фазовой ошибки в раскрыве (5) находим средний квадрат ошибки поверхности по нормали:

                     ,         (9)

 

откуда среднеквадратическое отклонение рефлектора по нормали к его поверхности равно

                                  .                                       (10)

 

Для примера, по формуле (10) получаем при δ= и F=D среднеквадратическое отклонение ≈.

 

3. Результаты моделирования

         Большинство двузеркальных антенн с электрическим сканированием имеют отношение фокусного расстояния эквивалентного параболоида к диаметру ≈1 [10]. Для расчетов диаметр зеркала примем равным D=30λ, а фокусное расстояние равным F=30λ, чтобы иметь =1. При таком диаметре зеркала метод физической оптики уже имеет высокую точность, в то же время электрический размер не очень велик, что позволяет провести расчеты быстро. Отношение  определяет угол облучения края зеркала и размер фокального пятна. Для оптимального облучения зеркала с =1 требуется круглый рупор с D_fed≈2λ. Для справки, критические диаметры круглого волновода для волн , ,  и  равны соответственно ≈0,586λ, ≈0,765λ, ≈0,972λ и ≈1,220λ. Поэтому все эти волны будут приниматься указанным рупором.

         Однозеркальная антенна с D=F=30λ и D_fed=2λ имеет расчетную ДН, в которой ширина по половинной мощности равна ≈2,28° в Е-плоскости и ≈2,13° в Н-плоскости. В диагональных плоскостях (φ=45°, 135°, 225° и 315°) максимальный уровень кросс-поляризации антенны равен минус 28,5 дБ, а для угла отклонения от оси 1° составляет порядка минус 35 дБ.

         Расчеты однозеркальной антенны в приемном режиме были выполнены при коническом сканировании источника под углом 1° к фокальной оси, соответствующим отклонению примерно на уровень половинной мощности ДН. Для полноты расчеты были проведены как для источника с линейной вертикальной поляризацией, так и для источников с левой круговой поляризацией и с правой круговой поляризацией. Были рассчитаны амплитуды и фазы принимаемых волн в рупоре для идеального параболоида и параболоидов с искажениями. Все результаты расчетов были нормированы таким образом, что амплитуды волн даются по отношению к максимальной амплитуде волны  для параболоида без искажений, фазы волн также даются относительно фазы волны  для параболоида без искажений (для угла φ=0°).

         На рисунках 2-7 показаны результаты расчетов для источника с вертикальной линейной поляризацией. Расчеты были проведены для зеркала без искажений и для регулярных фазовых искажений (5) с параметрами δ=, n=2. На рисунках 2 и 3 показаны амплитуды волн  и  соответственно. Для идеального параболоида амплитуда принимаемой волны  (главной поляризации) имеет небольшую амплитудную модуляцию из-за разных ширин ДН в Е и Н-плоскостях.

 

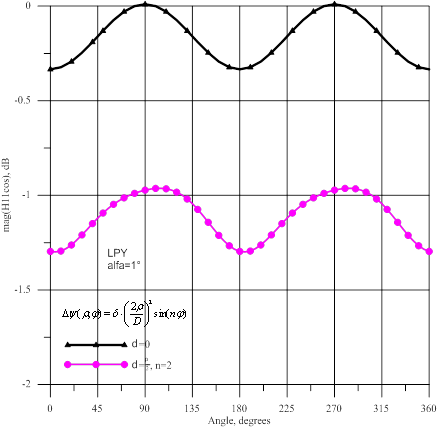
Рис.2- Амплитуда волны : источник с линейной вертикальной поляризацией

 

 

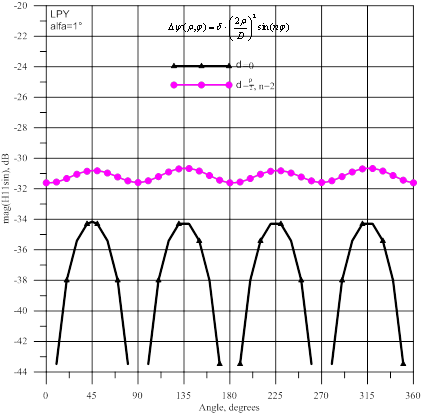
Рис.3- Амплитуда волны : источник с линейной вертикальной поляризацией

 

 

Рис.4- Амплитуда волны : источник с линейной вертикальной поляризацией

 

 

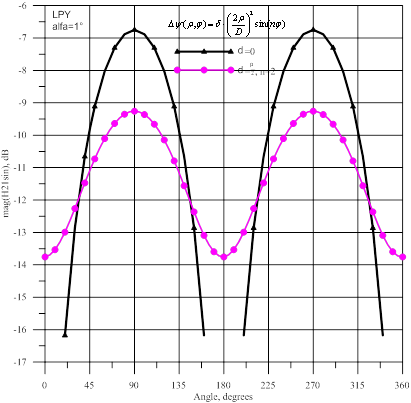
Рис.5- Амплитуда волны : источник с линейной вертикальной поляризацией

 

 

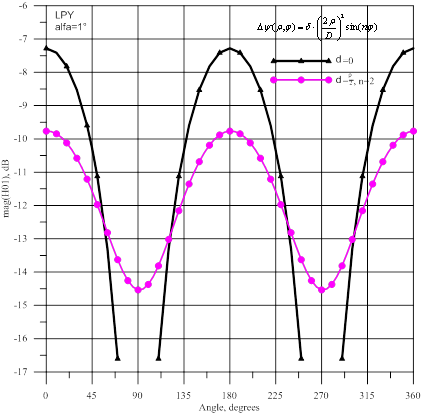
Рис.6- Амплитуда волны : источник с линейной вертикальной поляризацией

 

 

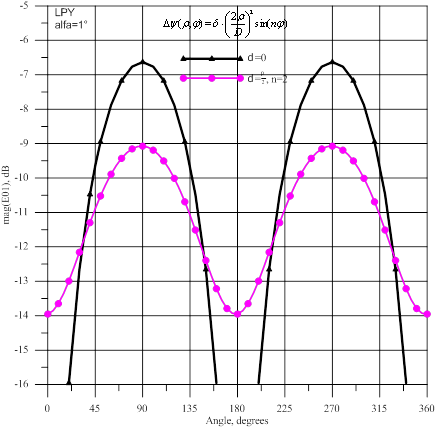
Рис.7- Амплитуда волны : источник с линейной вертикальной поляризацией

 

         Волна  не принимается в вертикальной и горизонтальной плоскостях, ее максимальный прием наблюдается в диагональных плоскостях, причем максимальная амплитуда примерно равна уровню кроссполяризации. Для параболоида с фазовыми искажениями амплитуда волны  снижается, а амплитуда волны  становится практически независимой от угла сканирования, ее уровень меньше уровня главной поляризации на ≈30 дБ. Данные результаты продемонстрировали известный эффект ухудшения поляризационной развязки в антенне с линейной поляризацией при фазовой ошибке в раскрыве. На рисунках 4 и 5 показаны амплитуды волн  и  соответственно, а на рисунках 6 и 7 показаны амплитуды волн  и  соответственно. Для идеального параболоида для этих высших мод существуют угловые направления, в которых волны в рупоре не возбуждаются при падении волны с линейной поляризацией. При наличии регулярных неосесимметричных фазовых искажений в зеркале нарушилась симметрия по квадрантам и нули для высших мод «заплыли».

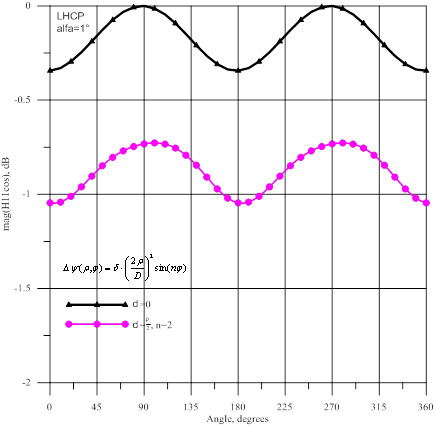
          На рисунках 8-13 показаны результаты расчетов для источника с левой круговой поляризацией. Расчеты были проведены для зеркала без искажений и для регулярных фазовых искажений (5) с параметрами δ=, n=2. На рисунке 8 даются амплитуды и фазы волны волн , а на рисунке 9- амплитуды и фазы волны волн . Для параболоида без искажений наблюдаются небольшая амплитудная модуляция (как и для источника с линейной поляризацией) и фазовая модуляция ≈±1° для обеих волн  и , вызванная кроссполяризацией. При наличии фазовых искажений наблюдается усиление фазовых осцилляций до ≈±8° и возникновение разницы ≈0,5 дБ между амплитудами  и . Фазовые соотношения между  и  таковы, что в рупоре возбуждается волна правой круговой поляризации (после отражения от зеркала вид поляризации изменяется).

 

 

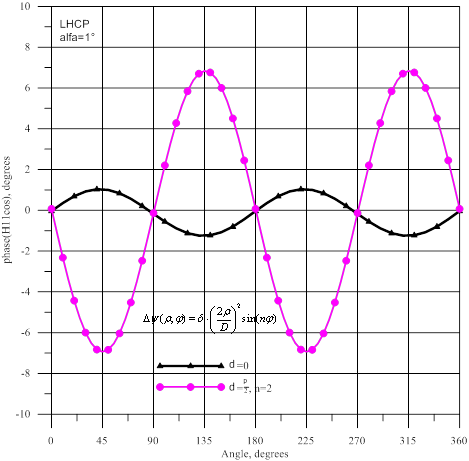
Рис.8- Амплитуда и фаза волны : источник с левой круговой поляризацией

 

 

 

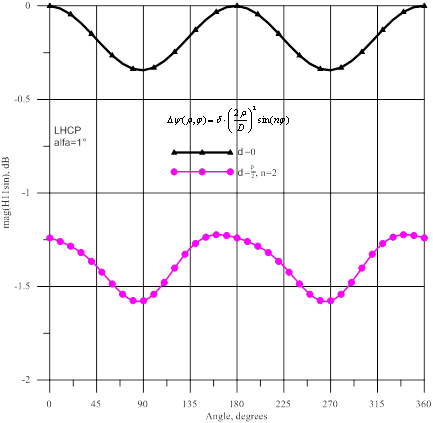
Рис.9- Амплитуда и фаза волны : источник с левой круговой поляризацией

 

 

 

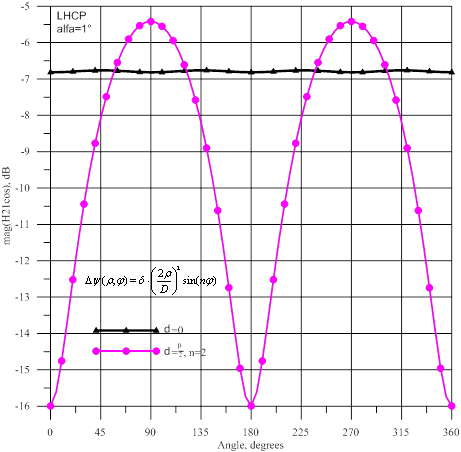
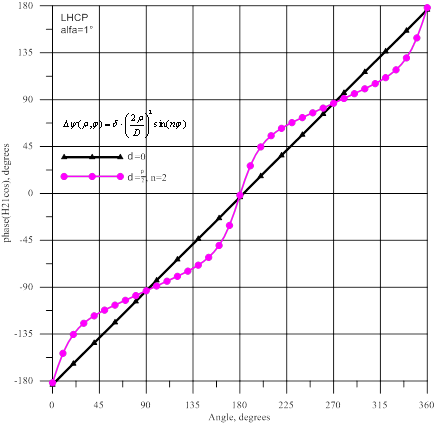
Рис.10- Амплитуда и фаза волны : источник с левой круговой поляризацией

 

 

 

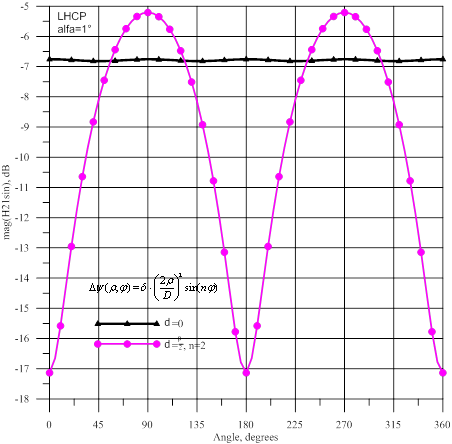
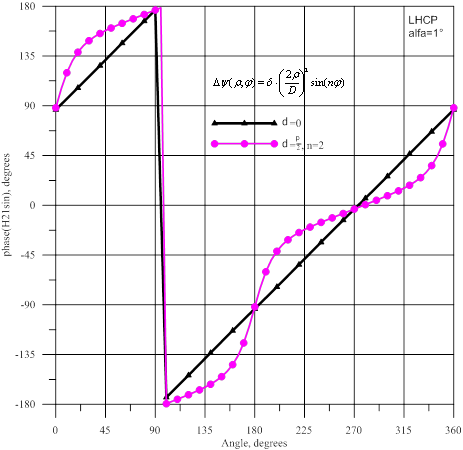
Рис.11- Амплитуда и фаза волны : источник с левой круговой поляризацией

 

 

 

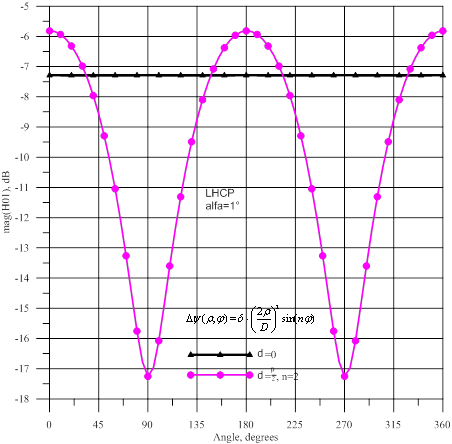
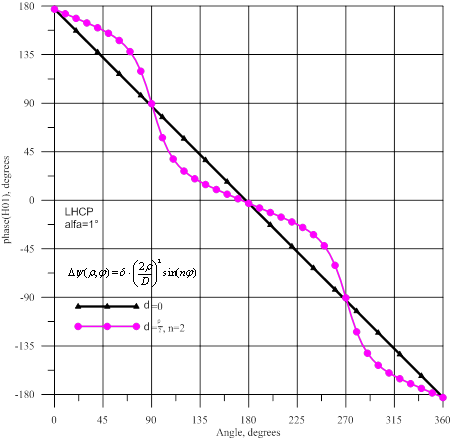
Рис.12- Амплитуда и фаза волны : источник с левой круговой поляризацией

 

 

 

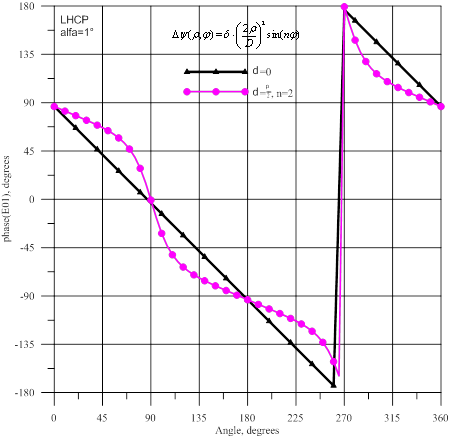
Рис.13- Амплитуда и фаза волны : источник с левой круговой поляризацией

 

         На рисунке 10 показаны амплитуды и фазы волны , а на рисунке 11- амплитуды и фазы волны . При наличии фазовых искажений в горизонтальной плоскости наблюдается уменьшение амплитуд  и  на ≈9,5 дБ, а в вертикальной плоскости- возрастание амплитуд на ≈1,5 дБ. Фазы  и  находятся в квадратуре, следовательно, эти волны могут быть объединены квадратурным мостом для формирования разностной ДН на круговой поляризации. На рисунке 12 показаны амплитуды и фазы волны , а на рисунке 13- амплитуды и фазы волны . Для этих волн, в отличие от волн , при наличии фазовых искажений в горизонтальной плоскости наблюдается возрастание амплитуд на ≈1,5 дБ, а в вертикальной плоскости- уменьшение амплитуд на ≈10 дБ. При коническом сканировании фазы высших мод изменяются по линейному закону. Для всех рассмотренных высших мод при искажениях зеркала возникают также фазовые осцилляции ≈±20° по отношению к соответствующим фазам для неискаженного зеркала.  

         На рисунках 14-19 показаны результаты расчетов для источника с правой круговой поляризацией. Расчеты были проведены для зеркала без искажений и для регулярных фазовых искажений (5) при трех комбинациях параметров: а) δ=, n=2; б) δ=, n=2; в) δ=, n=4. По сравнению с расчетами для левой поляризации были добавлены результаты для меньшей в два раза фазовой ошибки δ= и для 4-й гармоники фазовой ошибки (). На рисунке 14 даются амплитуды и фазы волны , а на рисунке 15- амплитуды и фазы волны . На рисунке 16 показаны амплитуды и фазы волны , а на рисунке 17- амплитуды и фазы волны . На рисунке 18 показаны амплитуды и фазы волны , а на рисунке 19- амплитуды и фазы волны .  

         Для источника с правой поляризацией при наличии фазовых искажений возникли аналогичные осцилляции амплитуд и фаз, что и для левой поляризации (рисунки 8-13). Разница в том, что произошел поворот на 90° для картин амплитудных осцилляций: теперь уменьшение амплитуд  и  происходит в вертикальной плоскости, а уменьшение амплитуд волн  и  в горизонтальной плоскости. Заметим, что при максимальной фазовой ошибке на краю раскрыва δ= амплитуды высших мод уменьшились не более чем на 3…3,5 дБ по сравнению с идеальным параболоидом. Для случая 4-й гармоники фазовой ошибки (δ=, n=4) глубоких нулей высших мод не наблюдается, происходит почти равномерное снижение их амплитуд для всех углов сканирования, фазовые осцилляции для высших мод почти нулевые. 

         На основании проведенных расчетов можно сравнить пеленгационные характеристики по значениям крутизны при разных высших модах, используемых для электрического сканирования на круговой поляризации. Если зеркало не искажено, то использование для сканирования пары волн  и  позволяет получить крутизну пеленгационной характеристики по напряжению выше в ≈1,4 по сравнению с системой сканирования с волной . Для рефлектора с искажениями с параметрами δ=, n=2 для источника с левой круговой поляризацией в антенне с электрическим сканированием с парой волн  и  существенно снизится крутизна пеленгационной характеристики в горизонтальной плоскости, а для антенны с электрическим сканированием с волнами  или  снизится крутизна пеленгационной характеристики в вертикальной плоскости. Если источник имеет правую круговую поляризацию, то эти плоскости поменяются местами.

 

 

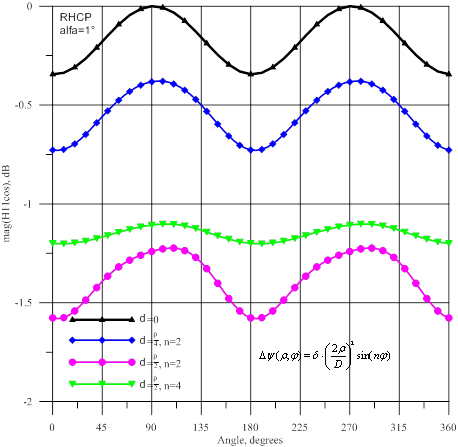
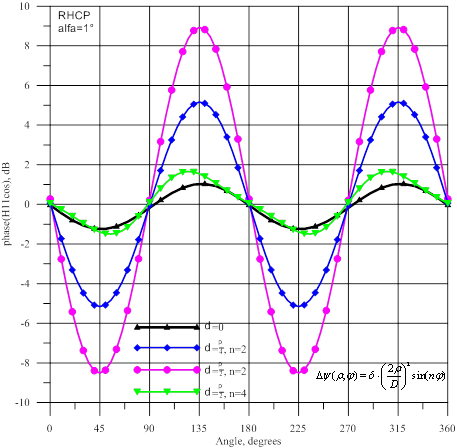
Рис.14- Амплитуда и фаза волны : источник с правой круговой поляризацией

 

 

 

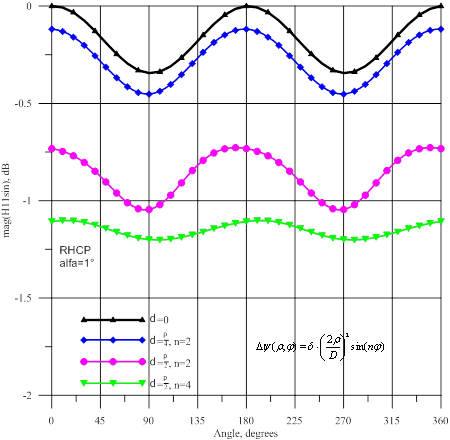
Рис.15- Амплитуда и фаза волны : источник с правой круговой поляризацией

 

 

 

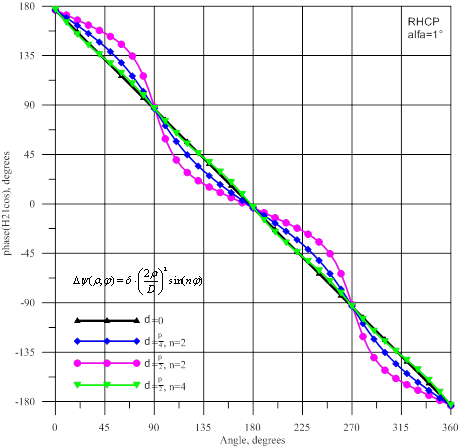
Рис.16- Амплитуда и фаза волны : источник с правой круговой поляризацией

 

 

 

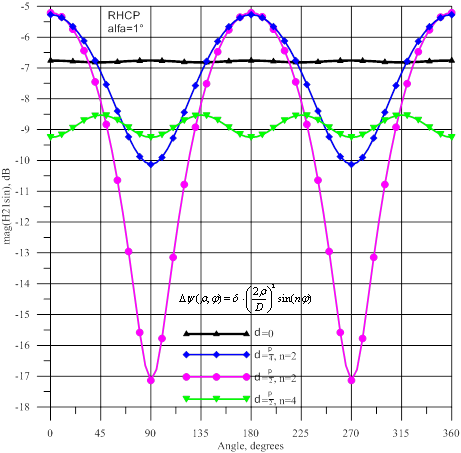
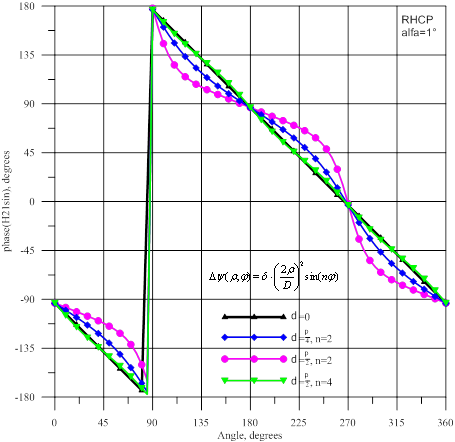
Рис.17- Амплитуда и фаза волны : источник с правой круговой поляризацией

 

 

 

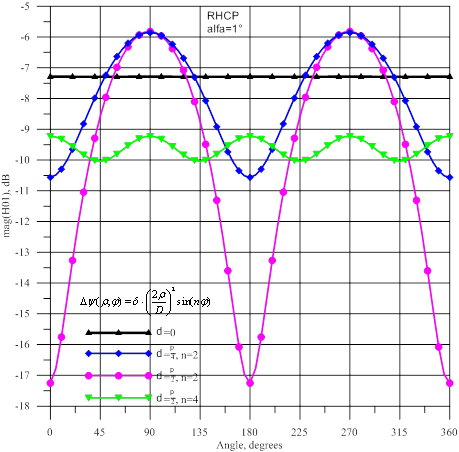
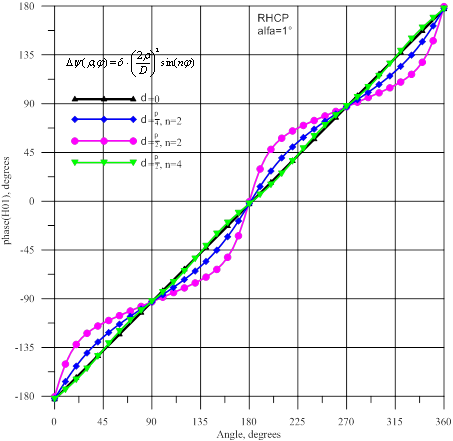
Рис.18- Амплитуда и фаза волны : источник с правой круговой поляризацией

 

 

 

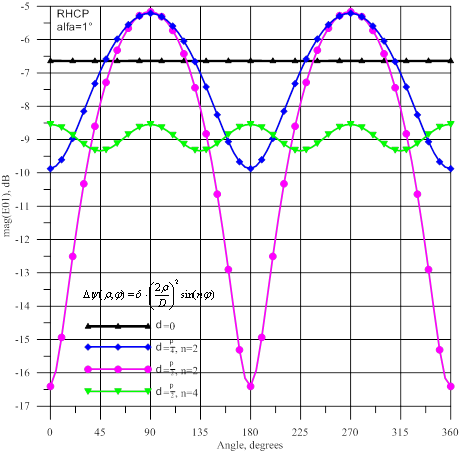
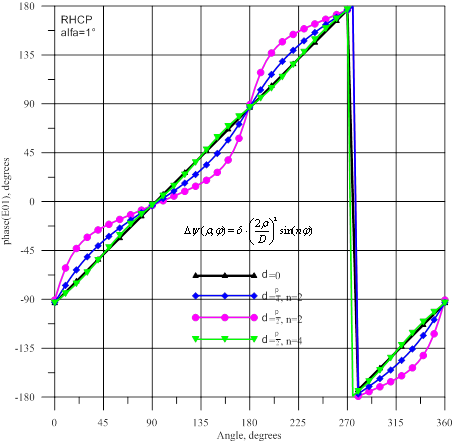
Рис.19- Амплитуда и фаза волны : источник с правой круговой поляризацией

 

4. Выводы

         Результаты расчетов зеркальной антенны с регулярными фазовыми ошибками в раскрыве при приеме волны с круговой поляризацией показали, что для зеркальных антенн с электрическим сканированием наиболее опасным видом регулярных фазовых искажений являются искажения типа «шляпа Наполеона», имеющие аналитическую формулу

                                    .                                              (11)

При такой фазовой ошибке в зеркале нарушается симметрия по квадрантам: в одной диагональной плоскости фазовая ошибка положительная, а в ортогональной диагональной плоскости- отрицательная. Заметим, что для высших мод, дающих разностные ДН, амплитудные распределения в раскрыве таковы, что максимумы имеются ближе к краю зеркала, поэтому они столь чувствительны к квадратической фазовой ошибке.

         При максимальной фазовой ошибке в раскрыве, равной , наблюдаются сильные осцилляции амплитуд высших волн ,  и . При коническом сканировании источника вокруг равносигнального направления амплитуды изменяются на ≈11,5 дБ. Осцилляции фаз высших мод составляют ≈±20°. Амплитудные осцилляции высших мод ,  и  приводят к тому, что крутизна пеленгационной характеристики существенно снижается для некоторых угловых направлений и, при дальнейшем увеличении фазовой ошибки, пеленгационная ось может исчезнуть. Если зеркало имеет такие значительные регулярные фазовые искажения, то никаким способом в облучателе нельзя добиться компенсации этого негативного явления. Электрическое сканирование нарушается при рассмотренных фазовых ошибках в зеркальной системе для системы автосопровождения, построенной на любой высшей моде круглого волновода.

         Допустимым уровнем фазовых искажений, при которых система автосопровождения будет работать удовлетворительно, можно считать искажения с δ=. При этом амплитуды высших мод уменьшаются из-за искажений не более чем на 3…3,5 дБ (в худшем случае) по сравнению с неискаженным зеркалом. Крутизна пеленгационной характеристики по напряжению по одной оси составит 70%, а по другой оси 120% по сравнению с идеальным параболоидом.

         Изготовитель в паспорте на рефлектор обычно указывает среднеквадратическое отклонение выполнения отражающей поверхности зеркала (СКО). На практике при изготовлении рефлектора имеют место и случайные, и регулярные отклонения. Если СКО рефлектора не превосходит максимальное значение ≈, соответствующее фазовой ошибке (11) с δ=, то рефлектор может использоваться для антенны с электрическим сканированием. Например, для λ=3 см получаем максимально допустимое СКО отражающей поверхности по нормали ≈0,75 мм.

         Несмотря на то, что исследование было проведено для рефлектора с диаметром D=30λ, выводы статьи справедливы для зеркальных антенн любого электрического размера.

 

Литература

1. Кантор Л.Я. Спутниковая связь и вещание. М.: Радио и связь, 1997, 528 с.

2. Imbriale W. Large antennas of the deep space network. (JPL Publication 02-6), February 2002.

3. Покрас А., Сомов А., Цуриков Г. Антенны земных станций спутниковой связи. М.: Радио и связь, 1985, 288 с.

4. Вальд В.П., Веревкин С.М., Попереченко Б.А., Соколов А.Е. Особенности антенных систем с электрическим сканированием для спутниковых систем связи.// Антенны, Вып.35, 1988, с.34-42, Радио и связь.

5. Choung Y., Goudey K., Bryans L. Theory and design of Ku-band TE21-mode coupler.// IEEE Trans. on MTT, 1982, Vol.30, No.11, pp.1862-1866.

6. Multi-mode tracking antenna feed system. United States Patent No.4,420,756, Dec. 13, 1983.

7. Holzman A., Eisenhart R., Robertson S., Kurtz L., Kihm R. A low cost Ka-band Cassegrain polarimetric tracking antenna. //Antennas and Propagation Society International Symposium, 1992. AP-S. 1992 Digest. Vol.1, pp.16-19.

8. Шифрин Я.С. Вопросы статистической теории антенн. М.: Сов. радио, 1970, 384 с.

9. Фролов В.П., Вальд В.П. Зеркальные антенны для земных станций спутниковой связи. М.: Горячая линия- Телеком, 2008, 496 с.

10. Жук М.С., Молочков Ю.Б. Конструирование антенно-фидерных устройств. М.: Энергия, 1966, 648 с.

11. Бодров В.В. Разработка алгоритмов расчета электромагнитных полей устройств СВЧ. М.: МЭИ, 1986, 56 с.