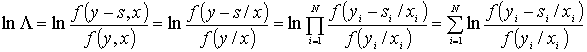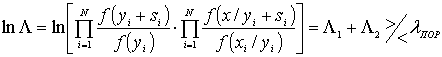Двухканальный обнаружитель полезных сигналов на фоне негауссовых помех

ДВУХКАНАЛЬНЫЙ ОБНАРУЖИТЕЛЬ ПОЛЕЗНЫХ СИГНАЛОВ НА ФОНЕ НЕГАУССОВЫХ ПОМЕХ

Филиал “Московский центр автоматизированного управления воздушным движением” ФГУП “Госкорпорация по ОрВД

Аннотация. В работе представлены варианты функциональных схем двухканальных обнаружителей сигналов, входящих в состав активно-пассивной системы РТС, а также рассмотрен алгоритм компенсации мешающих сигналов и помех имеющих негауссовы законы распределения. Для каждого канала приведены характеристики обнаружения.

Ключевые слова: негауссова помеха, отношение правдоподобия, межпунктовая корреляция, отношение правдоподобия.

Abstract. Options of function charts of two-channel detectors of the signals which are a part of active and passive radio engineering system are presented in the wrk and also the algorithm of compensation of the disturbing signals and hindrances having ungaussian laws of distribution is considered. For each channel characteristics of detection are provided.

Keywords: ungaussian hindrance, credibility relation, cross points correlation, credibility relation.

Введение

Полезные сигналы, принимаемые антеннами различных радиотехнических систем (РТС), например, навигационных, гидроакустических и т.д. сильно зашумлены мешающими сигналами и помехами, (МСиП). Следует отметить, что спектры МСиП занимают различные по ширине полосы частот, а законы вероятностей часто имеют негауссово распределение. МСиП с негауссовыми законами распределения можно разделить на две группы – импульсные и синусоидальные. К импульсным относятся атмосферные и индустриальные помехи, зондирующие сигналы наземных и бортовых импульсных радиолокационных станций (РЛС), а также сигналы бортовых ответчиков, выдающих информацию для систем управления воздушным движением (УВД). Примерами синусоидальных МСиП можно считать излучаемые несущие с произвольными законами угловой модуляции. В настоящее время известен метод компенсации, основанный на пространственной режекции МСиП. 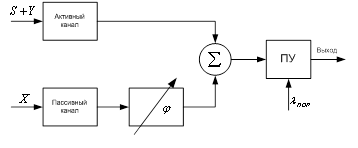Он заключается в том, что антенный блок РТС (рис.1) состоит из активной антенны, которая принимает аддитивную смесь полезного сигнала и помехи по основному лепестку диаграммы направленности (ДН):

(1)

и пассивной антенны, основной лепесток ДН которой принимает только сигнал помехи:

(2)

Далее сигнал помехи (2) с антенны пассивного канала поступает на фазовращатель, в котором его фаза меняется на противоположную, относительно фазы помехи принимаемой антенной активного канала. Затем аддитивная смесь (1) и помеха (2) с выхода фазовращателя поступают на сумматор, на выходе которого присутствует смесь:

где - остаток компенсации помехи.

Рис.1. Активно-пассивная система пространственной режекции помех.

Практически данный метод используется для построения антенных постов спутниковой связи, а также был применен при построении антенной системы американского военного спутника DSCS-3 [1]. Однако геометрические размеры антенных систем используемых в наземных РТС делает неприемлемым использование метода пространственной режекции МСиП в подвижных сегментах связных и навигационных систем, а также на борту летательного аппарата. В этом случае пространственную обработку принимаемых сигналов необходимо заменить временной обработкой, перенеся ее в узлы приемного тракта бортовой РТС.

В данной работе синтезируется алгоритм обнаружения полезных сигналов активно-пассивной системой с компенсацией негауссовых помех.

1. Функциональные схемы обнаружителей полезного сигнала с компенсацией МСиП

Алгоритмы выделения сигналов на фоне негауссовых помех зависят от пространственных параметров помех и сигналов. Допустим, что произвольная смесь амплитудно-фазоманипулированных процессов (АФМП) с произвольной модуляцией по огибающим и фазам имеет негауссову и нестационарную многомерную плотность вероятностей, которую в матричной форме можно записать:

, (3)

где - вектор-строка амплитуд АФМП, - вектор-столбец фаз АФМП, - многомерная плотность вероятностей помех на входе РТС. Достоинство такой записи – раздельное влияние на многомерную плотность огибающей АФМП амплитудных и фазовых составляющих. Для активно-пассивной РТС приема и обработки сигналов, рис.1, оптимальный алгоритм обнаружения можно записать в виде:

где и плотности вероятностей входных процессов активного и пассивного пунктов соответственно, - заданное значение порога обнаружения, - знак транспонирования.

Таким образом, оптимальный обнаружитель полезного сигнала функционально состоит (рис.2) из двух измерительных усилителей, двух нелинейных компенсационных блоков , являющихся нелинейно-инерционными преобразователями - и , весового матричного накопителя , параметры которого зависят от матрицы фазовых параметров МСиП, формируемой процессором и процессора формирующего матрицу значений огибающей (рис. 2).

Рис. 2. Выделение фаз огибающих амплитуд.

Предполагается, что в схеме обнаружителя рис. 2 автоматически производится и адаптация при неизвестных ранее законах фазовых и амплитудных модуляций. Приведенная схема может оказаться довольно сложной в технической реализации, поэтому в адаптивном варианте предпочтение может быть сделано схеме выполненной по рис. 3, в которой производится оценка априорных неизвестных многомерных плотностей вероятностей помех активных и пассивных приемных пунктов.

Рис.3. Формирование статистических характеристик помех.

При обнаружении слабых сигналов алгоритм обнаружения упрощается и может быть представлен в 2-х эквивалентных формах. Так, разлагая функцию в ряд Тейлора по и ограничиваясь 2-мя первыми членами при разложении, получаем:

где есть вектор-столбец переменных [2]. Обнаружитель состоит из многомерного нелинейно-инерционного преобразователя вектора помех и нелинейного матричного накопителя обладающего дискретной импульсной характеристикой (рис. 4).

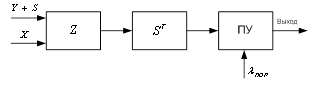
Рис.4. Обнаружитель с накопителем сигнала.

Другой вариант обнаружителя изображен на рис.5.

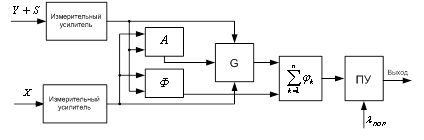
Рис.5. Обнаружитель с учетом фазовых свойств помех.

В нем реализуется алгоритм обнаружения, выражение для которого запишем в следующем виде:

где - матрица фаз МСиП, - матрица полезного сигнала, - знак транспонирования. Особенностью схемы (рис.5) является то, что в блоке сумматора происходит взвешивание и формирование матрицы сигналов из входных копий сигнала . При этом на один вход сумматора поступает сформированный в блоке вектор помех , зависящий от вектора огибающих МСиП. На другой вход сумматора поступает сформированный в блоке вектор фазовых параметров МСиП. Следует отметить, что структура обнаружителя представленного на рис.5 содержит 4 процессора - , ,, и в отличие от структуры обнаружителя представленной на рис.4, однако она полнее воспроизводит характер вычислений. Тем не менее, для моделирования предпочтительнее использовать более простые структуры, если только а`приорно известны многомерные совместные законы распределения вероятностей помех активных и пассивных пунктов приема.

2. Характеристики обнаружения

Рассмотрим подробнее обнаружение сигнала на фоне широкополосной (белой) по спектру негауссовой помехи одним активным и одним пассивным пунктом (рис.1) в предположении взаимной межпунктовой корреляции помех с коэффициентом взаимной корреляции:

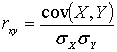где и - среднеквадратические отклонения помех и соответственно.

Тогда многомерное отношение правдоподобия распадается на произведения двумерных (взаимных) отношений, поэтому получаем:

. (4)

Следует отметить, что при коэффициенте корреляции условные негауссовы распределения допустимо аппроксимировать гауссовыми условными распределениями, вследствие этого получаем алгоритм с компенсацией помех и линейной фильтрацией сигналов, ничем не отличающийся от случая воздействия нормальных помех. Однако, такая ситуация наблюдается только при очень высокой межпунктовой корреляции . На практике часто не удается достичь такого коэффициента, поэтому аппроксимация условно гауссовыми распределениями является некорректной.

Для более точного решения задачи рассмотрим другой подход. Как известно из теории вероятностей:

Воспользуемся выражением из правой части равенства. Тогда отношение правдоподобия (4) запишем в виде:

, где

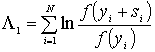, . (5)

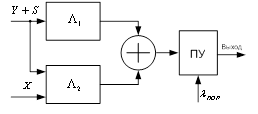
Функциональная схема обнаружителя полезного сигнала, работающего по такому алгоритму, представлена на рис. 6.

Рис. 6. Двухканальный обнаружитель сигнала.

Схема состоит из двух параллельных каналов, выходы которых суммируются и сравниваются с порогом для вынесения решения о наличии или отсутствии сигнала.

Рассмотрим сначала первый канал обнаружителя , который является нелинейным в силу негауссовости плотности вероятности помехи (3). Полагая для простоты сигнал слабым, ограничиваясь при разложении в ряд Тейлора функции первыми двумя членами (5), и учитывая формулу при условии что , получаем:

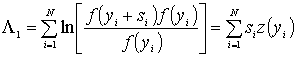, где .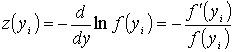

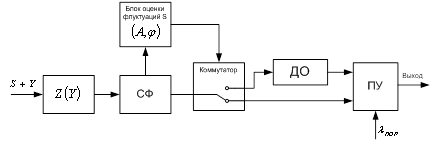
В состав функциональной схемы обнаружителя, которая представлена на рис. 7, входит блок, содержащий нелинейность без инерциальной цепи [3], согласованный с полезным сигналом фильтр (СФ), блок оценки флуктуаций полезного сигнала , детектор огибающей (ДО), включаемый в обработку при флуктуациях полезного сигнала, и пороговое устройство (ПУ).

Рис. 7. Функциональная схема нелинейного канала обнаружителя.

Наличие нелинейности приводит к резкому увеличению вероятности правильного обнаружения , особенно с ростом входного отношения сигнал/шум по мощности [2]:

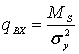где - мощность полезного сигнала, а - дисперсия помехи на входе приемника активного канала, равная средней мощности флуктуаций негауссовой помехи :

Конечно, так будет только при наличии оптимальной нелинейности , оптимизированной для известного распределения негауссовой помехи . Ясно также, что флуктуация параметров полезного сигнала ухудшает характеристики обнаружения.

Эти выводы следует обосновать. Будем полагать, что значение алгоритма , имеет нормальное распределение вероятностей. Тогда при отсутствии сигнала среднее значение равно нулю:

при ,

так как при четной плотности нелинейность является нечетной функцией. Действительно в среднем имеем:

Дисперсия случайной величины при отсутствии сигнала равна:

(6)

где величина равна:

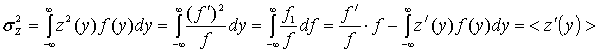так как в силу белости по спектру помехи при суммировании сохраняются только члены при условии [2]. В итоге для вероятности ложной тревоги при отсутствии на входе активного канала полезного сигнала получаем формулу:

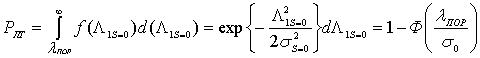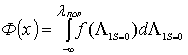где из (6), а - табулированный интеграл вероятностей.

При наличии сигнала среднее значение алгоритма равно:

а среднее значение принимает вид

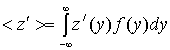и дисперсия, как нетрудно проверить равна:

. (7)

Поэтому для вероятности правильного обнаружения получаем выражение:

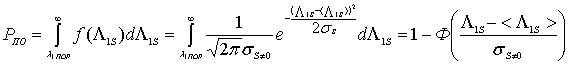, (8)

где величина из (7).

Рассмотрим примеры обнаружителей. Полагая сначала помеху гауссовой, получим уравнение нелинейности:

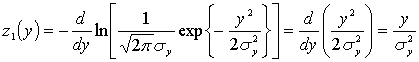В случае обнаружения сигнала на фоне ЧМ-помехи (шум с большой девиацией частоты), уравнение нелинейности будет равно:

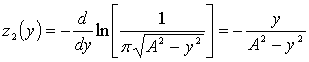т.е. получаем нелинейность экспандерного типа, линейную при условии и растянутую при условии , что способствует выделению слабого сигнала. И, наконец, при обнаружении сигнала на фоне импульсного и непрерывного шумов уравнение нелинейности принимает вид:

В этом случае получаем нелинейность типа жесткого ограничителя . Эта нелинейность относится к типу компрессионных, сжимающих диапазон выходных величин в интервале . В целом ограничитель аналогичен цепочке широкополосный фильтр – ограничитель – узкополосный фильтр (ШОУ), эффективной при выделении сигнала на фоне импульсной помехи [4], причем широкополосный фильтр на рис.7 не показан, а узкополосный фильтр есть СФ, повышающий качество обнаружения сигнала. Отметим еще, что компрессионная нелинейность превращается в экспандерную при замене оси абсцисс на ось ординат и наоборот. Отсюда вытекает и другой практически необходимый вывод. Используемые на практике непараметрические ограничители с жестким ограничением на входе являются оптимальными, если только помеха имеет экспоненциальное распределение вероятностей. И это несмотря на то, что при воздействии сигнала непараметричность, (т.е. независимость от параметров входной помехи) пропадает, т.е. некоторые параметры начинают зависеть от сигнала . Например, среднее значение процесса на выходе ограничителя при любой плотности имеет значение:

В силу симметрии плотности в точке получаем , по той же причине , поэтому среднее значение равно . В частности для экспоненциального распределения условие нормировки дает:

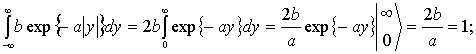
Поэтому среднее значение равно:

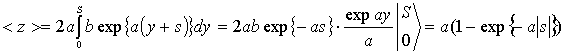и зависит от величины сигнала (при условии получаем ). Следует отметить, что суммарная мощность процесса на выходе жесткого ограничителя постоянна и независима от величины сигнала:

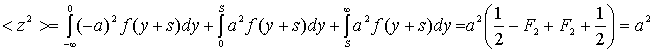
Поэтому дисперсия также не зависит от сигнала , и стремится к нулю только тогда, когда амплитуда детерминированного сигнала растет до бесконечности .

Теперь рассмотрим подробно второй канал обнаружителя (см. рис. 6) и алгоритм обнаружения в целом. Аппроксимируя, как и раньше, условные функции правдоподобия в числителе и знаменателе гауссовыми условными распределениями, после преобразования независимо от величины сигнала получаем:

, ,

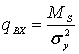; ; ; , (9)

где - отношение сигнал/шум на входе активного канала, - коэффициент пропорциональности между весами и , зависящими от коэффициента корреляции помех и .

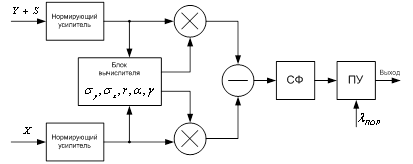
Рис. 8. Функциональная схема линейного канала обнаружителя.

Функциональная схема линейного канала обнаружителя представлена на рис.8. Она состоит из блока вычислителя, формирующего величины (9), перемножителей, блока вычитания, согласованного с полезным сигналом фильтра (СФ) и порогового устройства. С учетом нормировки помех получаем:

, ; .

Поэтому в идеале в среднем остаток компенсации помех равен нулю, а наличие сигнала на входе увеличивает приращение мощности сигнала в раз:

Объединим каналы, изображенные на рис. 6, 7 и 8, в единую схему обнаружителя. Учтем при этом, что СФ должен быть общим (рис. 9).

Рис. 9. Полная функциональная схема обнаружителя сигнала.

Если коэффициент корреляции , то компенсация автоматически отключается и работает один нелинейный канал. Если же , то эффективность компенсации линейного канала настолько высока, что вкладом от параллельного нелинейного канала можно пренебречь, особенно с увеличением мощности входного сигнала. Выражение объединенного алгоритма обнаружения запишем в виде:

В условиях высокой эффективности компенсатора помех при отсутствии сигнала на входе имеем , , и вероятность ложной тревоги почти не меняется. При наличии сигнала:

, ,

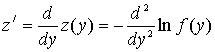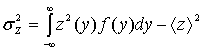
и вероятность правильного обнаружения (8) тем выше, чем больше отношение:

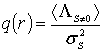3. Выводы

В результате проведенного анализа состояния техники пространственной режекции МСиП представлены структуры двухканальных приемников обнаружения полезных сигналов с компенсацией негауссовых МСиП.

Рассмотрена отдельно работа каждого приемного канала, а также даны характеристики обнаружения.

Литература

1. Верзунов Г. В., Ганзий Д. Д., Степанов А. А. Защита от радиопомех в спутниковой связи // Технологии и средства связи. – 2008. - №6. - С.90 - 93.

2. Голяницкий И. А. Оптимальная пространственно – временная обработка негауссовых полей и процессов. - М: Издательство МАИ, 1994. - 208 c.

3. Киреев М. А. Выделение полностью известного сигнала на фоне негауссовых помех //Телекоммуникации. – 2012. - №3. - С.13 - 18.

4. Лезин Ю. С. Введение в теорию и технику радиотехнических систем: Учеб. пособие для вузов.- М.: Радио и связь, 1986. - 280 с.