УДК 681.883

РЕШЕНИЕ ЗАДАЧИ «ОБНАРУЖЕНИЕ-ИЗМЕРЕНИЕ ДАЛЬНОСТИ» ДЛЯ МАЛОПОДВИЖНЫХ ОБЪЕКТОВ МЕТОДОМ АКТИВНОЙ КОРРЕЛЯЦИИ

С. В. Шостак ¹, Е. Н. Бакланов ², П. А. Стародубцев ³, А. П. Шевченко ³

¹ Дальневосточный федеральный университет

² Дальневосточный государственный технический рыбохозяйственный университет

³ Тихоокеанское высшее военно-морское училище имени С.О. Макарова

Статья получена 28 февраля 2015 г.

 

Аннотация. В работе рассмотрена возможность обеспечения необходимой разрешающей способности гидролокатора по дальности за счет кодирования зондирующих импульсов путем широкополосной модуляции, в противовес изменению их длительности. При этом обеспечивается более эффективное использование мощности излучателя и более высокая помехоустойчивость. Предложен метод активной корреляционной обработки эхо-сигналов, принимаемых от нескольких целей и перекрывающихся во времени, суть которого заключается в преобразовании временного сдвига сигнала в частотный и использовании референтного сигнала, зависящего от параметров зондирующего импульса и диапазона измеряемой дальности.

Ключевые слова: гидролокатор, разрешающая способность, корреляционная обработка сигнала, линейная частотная модуляция, референтный сигнал

Abstract: In this article we consider the possibility of providing the necessary resolution in range  of a sonar due to encoding pulses through broadband modulation, as opposed to a change in their duration. This provides more efficient use of a transmitter power and a high noise immunity. We propose a method of active correlation processing of echo signals received from multiple targets and 
overlapping in time, the essence of which is to convert the temporary shift of the signal into the frequency signal and to use the reference signal, which depends on the parameters of the pulse and the band of the measured range.

Key words: conar, range resolution, correlation processing of signal, linear frequency modulation, reference signal.

 

В импульсных гидролокационных системах параметры зондирующего импульса обычно представляют собой компромисс между желанием получить лучшее разрешение по дальности, что связано с необходимостью иметь возможно меньшую длительность импульса, и стремлением добиться максимально возможной дальности обнаружения, что требует максимизации энергии импульса за счет использования как можно более длинных импульсов. Вместе с тем, в фундаментальной работе Вудворта установлено, что форма сигнала является дополнительным параметром при разработке гидролокатора и что такие характеристики, как дальность и разрешение по дальности, могут определяться не только средней излучаемой мощностью и длительностью излучаемого импульса, но и формой сигнала [1]. Идеи развитые Вудвортом означают, что длительность излучаемого импульса может быть такой, какая необходима для удовлетворения энергетических требований. После удовлетворения требований к характеристикам обнаружения можно обеспечить условия для получения необходимого разрешения по дальности за счет кодирования излучаемого сигнала путем широкополосной модуляции. Одним из наиболее важных вкладов Вудворта в развитие современной теории сигналов было установление того, что разрешение по дальности и точность измерений определяются шириной полосы сигнала, а не его длительностью.

Для извлечения полезной информации, содержащейся в сигнале описываемого типа, требуется использовать более сложные методы обработки по сравнению с методами для простого импульсного сигнала. Такие методы известны как методы согласованной фильтрации, методы корреляционной обработки. Способность варьировать и подбирать в соответствии с теми или иными требованиями различные характеристики сигнала является важным фактором развития современных гидролокационных систем, использующих сложные методы обработки. При помощи этих методов достигается более эффективное использование средней мощности, которую можно получить от излучателя, более высокая разрешающая способность по дальности и по скорости, повышение помехоустойчивости по отношению к определенным типам интерферирующих сигналов, свойства которых отличаются от свойств кодированных сигналов, также имеется возможность оценки параметров сигналов, несущих информацию о дальности, скорости и, возможно, ускорении объектов.

Такие методы обработки реализуются путем корреляционного сравнения принимаемого сигнала с копией зондирующего сигнала, имеющейся в приемнике. При этом предполагается, что копия представляет собой зондирующий сигнал, форма которого изменена в зависимости от ожидаемых задержки и/или доплеровской частоты [2]. Поэтому в приемнике должен иметься банк различных копий. Это значительно увеличивает как сложность алгоритмов обработки сигналов, так и самого приемного устройства.

Для увеличения полосы частот в основном используются частотные или фазомодулированные сигналы [1,2].

Рассмотрим применение сигналов с линейной частотной модуляцией (ЛЧМ) для измерения дальности малоподвижных объектов с высоким разрешением по дальности методом активной корреляционной обработки. Техника такой обработки состоит из следующих процедур: принятый сигнал дискретизируется, смешивается с референтным, фильтруется низкочастотным фильтром, и, наконец, полученный дискретный сигнал пропускается через гребенку узкополосных фильтров. Гребенка узкополосных фильтров необходима для извлечения тонов, которые пропорциональны дальности до цели. Такая обработка эффективно преобразовывает временную задержку, соответствующую дальности, в частоту. Все принятые сигналы с одной и той же дальности будут иметь одинаковую постоянную частоту. На рисунке 1 представлена блок-схема устройства измерения дальности методом активной корреляции. Его работа будет рассмотрена далее.

Рис. 1. Блок-схема устройства измерения дальности методом активной корреляции

 

Рассмотрим более подробно принцип работы приемника с активной корреляционной обработкой, когда принимаются эхо-сигналы от нескольких целей при условии, что сигналы перекрываются во времени.

Нормализованный излученный сигнал может быть представлен выражением

                                      (1)

где     - начальная частота;

 – коэффициент девиации частоты;

 - полоса частот;

 - длительность сигнала.

Предполагаем, что точечный рассеиватель находится на расстоянии R. Тогда отраженный сигнал в приемнике будет иметь вид

         ,                           (2)

где     – коэффициент, учитывающий отражающую способность цели, усиление антенны и потери на распространение.

Временная задержка  определяется соотношением

.                                                                                   (3)

В свою очередь референтный сигнал имеет такую же форму, как и излученный

                                          (4)

где     - начальная частота;

 – длительность референтного сигнала.

Он существует в приемном окне, длительность которого вычисляется из разности максимальной и минимальной дальности измерения, т.е.

         ,                                                  (5)

где     – максимальная измеряемая дальность;

 – минимальная измеряемая дальность;

 – диапазон дальности, соответствующий окну приема.

На выходе смесителя после смешивания эхо-сигнала с референтным будет сформирован сигнал следующего вида:

 

,

(6)

 

где

         .                                                                              (7)

Положим , тогда выражение (6) будет

      (8)

и после низкочастотной фильтрации получим

                                                                        (9)

После подстановки (3) в выражение (9),  приобретает вид

                          (10)

Мгновенная частота такого сигнала равна

                                                              (11)

 

Процедуры смешивания с референтным сигналом и низкочастотная фильтрация эквивалентны вычитанию мгновенной частоты эхо-сигнала из мгновенной частоты референтного сигнала. Поэтому выход низкочастотного фильтра состоит из одного или нескольких тонов (в случае нескольких разных дальностей), соответствующих дальностям до целей. Выражение (11) для мгновенной частоты показывает, что дальность до цели пропорциональна мгновенной частоте, которая является константной. Последующее вычисление спектральной плотности мощности приводят к выводу, что пик на некоторой частоте  указывает на присутствие цели на дальности

         .                                                                                               (12)

Предположим, что имеется  целей, находящихся на дальностях  Cчитаем также, что  и эхо-сигналы от этих целей перекрываются во времени. Исходя из принципа суперпозиции, общий сигнал можно определить выражением

         ,                              (13)

где     - коэффициенты, учитывающие отражающие способности цели, усиление антенны, потери на распространение.

Времена  представляют временные задержки,  - совпадает с началом окна приема. Используя выражение (10), общий сигнал выхода низкочастотного фильтра может быть представлен как

         .                        (14)

 

И следовательно, наличие эхо-сигналов проявляется в появлении постоянных частотных тонов, которые могут выделяться гребенкой узкополосных фильтров. В цифровой обработке сигналов для обнаружения тональных сигналов широко применяется Дискретное Преобразование Фурье (ДПФ), которое реализуется на основе алгоритма Быстрого Преобразования Фурье (БПФ) [3]. По этой причине определение соответствующей частоты дискретизации и размеры БПФ критичны для изложенного метода.

         Так как метод активной корреляционной обработки целесообразно применять для ЛЧМ сигналов со значительной полосой частот, то приемное окно по этой причине имеет ограничения на размеры. Как известно, при использовании техники сжатия импульсов разрешение по дальности определяется выражением [4].

         .                                                                                            (15)

Будем считать, что БПФ имеет размер  и его частотное разрешение имеет величину .

Рассмотрим два точечных рассеивателя, находящихся на одном направлении и на дальностях  и . Минимальное частотное разрешение , чтобы рассеиватели разделялись, может быть найдено из (11). Более точно,

.                                                 (16)

Подставляя значение для , получим

         .                                                                                      (17)

 

Максимальная разрешаемая частота БПФ ограничена областью . Таким образом, максимальная разрешаемая частота определяется выражением

.                                    (18)

Подставляя выражения для  и  в (18), окончательно получим

         .                                                                                              (19)

Для наилучшей реализации БПФ его размер выбирается кратным 2 и тогда

,

где     - натуральное число.

Соответственно интервалы дискретизации в частотной и временной областях будут определяться выражением

         ,                                                                   (20)

 

где     – интервал дискретизации в области времени.

         Исходя из теории дискретной фильтрации и свойств ДПФ, можно заметить, что формулы, описывающие эти два процесса весьма схожи, так как в обоих случаях они представляют собой линейную комбинацию отсчетов входного сигнала [3]. Это говорит о том, что ДПФ можно трактовать как обработку сигнала фильтром с соответствующей импульсной характеристикой. Формула, описывающая прямое ДПФ, имеет следующий вид:

         ,                                                                (21)

где     – номер отсчета во временной области;

          - номер отсчета в частотной области;

          - дискретный сигнал в области времени.

Импульсную характеристику такого фильтра можно получить, если учесть, что  при целочисленном , и с учетом этого записать формулу ДПФ следующим образом:

         .                                        (22)

 

Преобразованная таким способом формула ДПФ представляет собой дискретную свертку, то есть N-й отсчет результата обработки входного сигнала  фильтром, импульсная характеристика которого равна

         .                                   (23)

 

Импульсная характеристика для каждого частотного отсчета ДПФ своя, поэтому в ее обозначении использован индекс k.

         Определим частотную характеристику такого фильтра и оценим его полосу пропускания. Для этого зафиксируем некоторый индекс , соответствующий частоте , и возьмем ДПФ от . В результате получим частотную характеристику

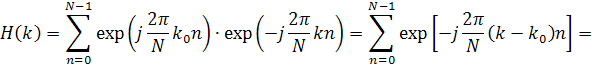
.                                   (24)

 

Так как  и , то выражение для АЧХ можно записать как

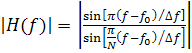         ,                                                               (25)

 

откуда несложно получить, что ширина полосы такого фильтра равна . В результате, тональный сигнал, фиксирующий факт наличия цели и определяющий дальность до нее, попадает в один из  фильтров.

Проведем оценку отношения сигнал/шум на выходе рассмотренного приемника.

Считаем, что на входе присутствует стационарный «белый» шум с дисперсией , где  - спектральная плотность мощности шума.

Так как эхо-сигнал присутствует «редко», то при непрерывном наблюдении случайных флуктуаций шумового сигнала внимание концентрируется на кратковременных отклонениях от усредненного за длительный период или среднеквадратического значения шума [1,2]. Поэтому отношение сигнал/шум, которое чаще всего используется при решении локационных задач, определяется как отношение мгновенной пиковой мощности выходного сигнала и выходной мощности шума [1,2,4]. Применим это определение для вышеизложенного способа.

Как известно, энергия принимаемого сигнала с прямоугольной огибающей равна

,                                                               (26)

где     и  – амплитуда и длительность сигнала соответственно. Мощность стационарного «белого» шума на входе приемника имеет величину

         .                                                                 (27)

Так как в нашем случае анализ проводится в элементарной полосе , то выходная мощность шума определяется . При этом, как ранее указывалось, . В результате, отношение сигнал/шум, согласно определению, имеет вид

         .                                            (28)

 

Так как выделенный гармонический сигнал находится в полосе , то в соответствии с равенством Парсеваля его энергия в области частот определяется соотношением

         ,                                            (29)

где     – преобразование Фурье выделенного тонального сигнала;

          – модуль .

Известно, что ширина полосы гармонического сигнал обратно пропорциональна длительности сигнала [2]. По этой причине, согласовывая интервал дискретизации по частоте  с длительностью сигнала, можем записать, что

         .                                 (30)

И тогда соотношение сигнал/шум сводится к

         .                                                                  (31)

 

Учитывая, что  и , окончательно получим

         .                                                                (32)

 

         Полученное соотношение (32) полностью совпадает с известным соотношением сигнал/шум в случае согласованной фильтрации, или корреляционной обработки [1,2,4]. Вместе с тем необходимо отметить, что в рассмотренном методе как обнаружение объекта, так и измерение его дальности проводятся в частотной области.

Рассмотрим более подробно работу устройства измерения дальности, блок-схема которого представлена на рис. 1.

Представленное устройство содержит следующие элементы:

SG1 - генератор зондирующего сигнала, формирует сигнал в дискретном виде;

DAC           - цифро-аналоговый преобразователь, преобразует цифровой сигнал в аналоговый;

BF1   - полосовой фильтр, удаляет помехи и выделяет аналоговый сигнал в заданной полосе;

Amp.1        - усилитель, усиливает сигнал перед подачей его на излучатель;

Amp.2        - усилитель, усиливает принятый эхо-сигнал;

BF2   - полосовой фильтр, выделяет эхо-сигнал в заданной полосе;

ADC           - аналого-цифровой преобразователь, проводит дискретизацию аналогового сигнала;

mixer          - смеситель, осуществляет перемножение референтного сигнала и эхо-сигнала;

LF     - низкочастотный фильтр, выделяет низкочастотную составляющую разностной частоты, которая содержит информацию о дальности;

SDP - блок вычисления спектральной плотности мощности, ось частот является шкалой дальности и градуируется в единицах длины;

CU    - устройство управления, предназначено для синхронизации работы отдельных блоков;

PC     - персональный компьютер, функции блоков, охваченных пунктирной линией, могут быть реализованы в персональном компьютере.

Генератор зондирующего сигнала (SG1) по команде из устройства управления (CU) формирует в цифровом виде ЛЧМ сигнал с заданными параметрами (начальная частота, полоса частот, длительность). Цифро-аналоговый преобразователь (DAC) преобразует сигнал из цифровой формы в аналоговую и подает его в полосовой фильтр (BF1). Так как в результате преобразования «цифра-аналог» появляются помехи, то BF1 выделяет сформированный аналоговый сигнал в заданной полосе частот, после чего сформированный зондирующий ЛЧМ сигнал усиливается в усилителе (Amp.1) и излучается. В это же время по команде CU запускается генератор референтного ЛЧМ сигнала, который имеет такие же начальную частоту и коэффициент девиации, что и зондирующий сигнал, но отличающийся длительностью и полосой частот, которые определяются по заданному диапазону дальности.

Принятый эхо-сигнал усиливается усилителем (Amp.2) и подается в полосовой фильтр (BF2), где сигнал отфильтровывается в заданной полосе от шума среды. Далее сигнал подается в аналого-цифровой преобразователь (ADC), где он приводится к цифровому виду, и затем поступает в смеситель (mixer). В смесителе эхо-сигнал перемножается с референтным, который подается из SG2. В результате образуются две составляющие сигнала. Одна составляющая разностной частоты, которая используется для измерения дальности, и другая высокочастотная составляющая суммарной частоты. Низкочастотный фильтр (LF), куда сигнал подается с выхода смесителя, выделяет низкочастотную разностную составляющую и подавляет высокочастотную составляющую. Далее низкочастотная составляющая подается в блок вычисления спектральной плотности мощности (SDP). Операция вычисления спектральной плотности мощности реализуется на основе алгоритма Быстрого Преобразования Фурье (БПФ), когда вычисляется ДПФ (Дискретное Преобразование Фурье) и затем вычисляется его квадрат модуля [3]. При этом частотная ось градуируется в единицах измерения дальности. Синхронизация работы отдельных блоков устройства осуществляется устройством управления (CU).

Заключение

В современных гидролокаторах для решения задач обнаружения сигналов и измерения их параметров, несущих информацию о дальности и скорости цели, используют различные виды сигналов и методы их обработки. При этом основным методом является метод согласованной фильтрации, или корреляционный метод. Метод корреляционной обработки позволяет сжимать сигнал во времени, концентрируя энергию сигнала в узком диапазоне и увеличивая тем самым отношение сигнал/шум на выходе приемника, что ведет к повышению вероятности правильного обнаружения, улучшению разрешающей способности и точности измерений. При решении определенных задач и, соответственно, выборе для этого некоторого сигнала проводится анализ потенциальных возможностей сигналов с применением основных положений функции неопределенности, из которых следует, что наилучшими сигналами в задачах «обнаружение-измерение» являются такие, у которых функция неопределенности имеет кнопочный вид [1,2,4]. В то же время такие сигналы имеют особенность, когда их временная структура чувствительна к искажениям канала распространения. Поэтому для успешного применения техники корреляционной обработки необходим банк копий сигналов, определенным образом учитывающих влияние канала, что непросто сделать для сигналов со сложенной фазовой модуляцией. В противном случае ожидаемого положительного эффекта не будет.

Влияние гидроакустического канала на распространение звука заключается в наличии таких факторов, как многолучевость, что может приводить к федингу в случае простых гармонических сигналов, и в наличии  ложно заполненных пассивных отражателей, что вызывает реверберацию. В ряде работ проведен анализ обработки сигналов для указанных факторов и получены результаты, указывающие, что сигнал в таком случае должен иметь плоскую спектральную плотность [1,5,6]. Сигналом, удовлетворяющим такому требованию, является ЛЧМ сигнал.

В выполненной работе приведен метод корреляционной обработки ЛЧМ сигнала. Суть этого метода заключается в преобразовании временного сдвига сигнала в частотный. Для этого в приемнике формируется специальный референтный сигнал с параметрами, которые зависят от параметров зондирующего и от диапазона измеряемой дальности, что отличает этот метод от известных методов корреляционной обработки. Данный метод отличается от известных отсутствием банка копий (или многоканальности) и простотой реализации. При этом он сохраняет все достоинства техники корреляционной обработки. Метод активной корреляции кроме обнаружения сигналов, позволяет измерять дальность до целей с высокой разрешающей способностью, что делает возможным применять в задачах томографии.

Устойчивость структуры ЛЧМ сигналов к искажениям в гидроакустическом канале позволяет применять их и при решении задач навигационного ориентирования подводных аппаратов. Однако при наличии доплеровского эффекта данный метод будет давать ошибку по дальности, хотя и небольшую. Но так как подводные аппараты имеют, как правило, скорости не более 3 узлов, то метод активной корреляции вполне применим для их навигационного ориентирования.

 

Литература

1.       Кук Ч., Бернфельд М. Радиолокационные сигналы. М.: Сов. Радио. 1971.

2.       Варакин Л.Е. Теория сложных сигналов. М.: Сов. Радио. 1970.

3.       Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. М.: Мир. 1978.

4.       Тихонов В.И. Оптимальный прием сигналов. М.: Радио и связь. 1983.

5.       Kay S., Optimal Signal Design for Detection of Gaussian Point Targets in Stationary Gaussian Clutter/Reverberation. Kingston, University of Rhode Island, 2007.

6.       Ван Трис Г., Теория обнаружения, оценок и модуляции. Т 3., М.: Сов. Радио. 1977.